Journal of Modern Physics
Vol.4 No.8(2013), Article ID:35799,9 pages DOI:10.4236/jmp.2013.48141
General Spin Dirac Equation (II)
Department of Applied Physics, National University of Science and Technology, Bulawayo, Republic of Zimbabwe
Email: physicist.ggn@gmail.com
Copyright © 2013 Golden Gadzirayi Nyambuya. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 10, 2013; revised May 13, 2013; accepted June 27, 2013
Keywords: Curved Spacetime Dirac Equation; General Spin Equation; Unified Field Theory
ABSTRACT
In an earlier reading [1], we did demonstrate that one can write down a general spin Dirac equation by modifying the usual Einstein energy-momentum equation via the insertion of the quantity “  ” which is identified with the spin of the particle. That is to say, a Dirac equation that describes a particle of spin
” which is identified with the spin of the particle. That is to say, a Dirac equation that describes a particle of spin 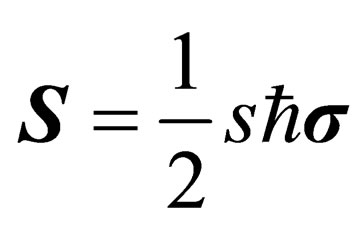 where
where  is the normalised Planck constant,
is the normalised Planck constant,  are the Pauli
are the Pauli  matrices and
matrices and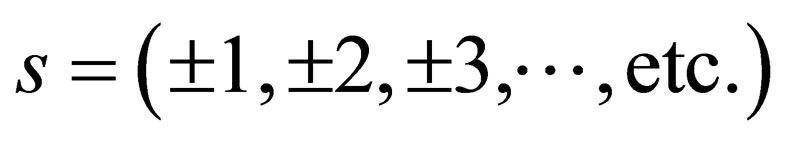 . What is not clear in the reading [1] is how such a modified energy-momentum relation would arise in Nature. At the end of the day, the insertion by the sleight of hand of the quantity “
. What is not clear in the reading [1] is how such a modified energy-momentum relation would arise in Nature. At the end of the day, the insertion by the sleight of hand of the quantity “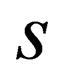 ” into the usual Einstein energy-momentum equation, would then appear to be nothing more than an idea belonging to the domains of speculation. In the present reading—by making use of the curved spacetime Dirac equations proposed in the work [2], we move the exercise of [1] from the realm of speculation to that of plausibility.
” into the usual Einstein energy-momentum equation, would then appear to be nothing more than an idea belonging to the domains of speculation. In the present reading—by making use of the curved spacetime Dirac equations proposed in the work [2], we move the exercise of [1] from the realm of speculation to that of plausibility.
1. Introduction
In an earlier reading [1], it is argued without a proper physical basis but more out of mathematical curiosity that the modified dispersion relation or the modified Einstein energy-momentum relation:
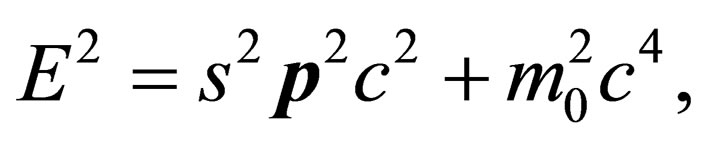 (1)
(1)
leads1 to a General Spin Dirac Equation. That is to say, the resulting Dirac equation describes a particle of spin 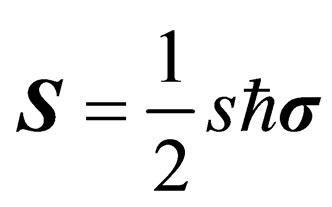 where
where  is the normalised Planck constant,
is the normalised Planck constant,
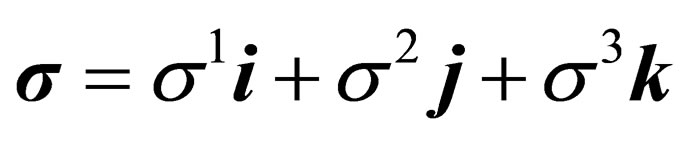 where
where 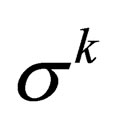 are the usual
are the usual 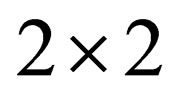 Pauli matrices and i, j, k are the three orthonormal basis on the
Pauli matrices and i, j, k are the three orthonormal basis on the 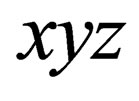 grid. In the dispersion relation (1.1),
grid. In the dispersion relation (1.1), 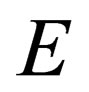 is the total energy of the particle,
is the total energy of the particle, 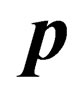 is its momentum,
is its momentum, 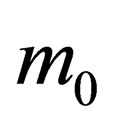 its rest mass and
its rest mass and 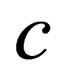 is the speed of light in vacuum. What is not clear in this reading [i.e. in Ref. 1] is how such an energy-momentum relation would arise in Nature in a manner that can be justified without making ad hoc and hand-waving arguments. At the end of the day, the insertion by the sleight of hand of the quantity “
is the speed of light in vacuum. What is not clear in this reading [i.e. in Ref. 1] is how such an energy-momentum relation would arise in Nature in a manner that can be justified without making ad hoc and hand-waving arguments. At the end of the day, the insertion by the sleight of hand of the quantity “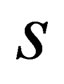 ” into the usual Einstein energy-momentum equation:
” into the usual Einstein energy-momentum equation:
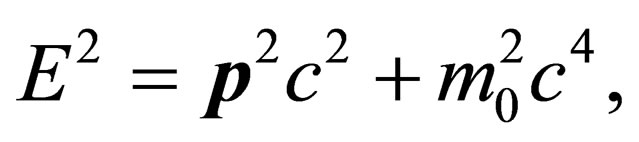 (2)
(2)
would then appear to be nothing more than a product of agile mathematical curiosity, speculation and chicanery, without anything to do with physical and natural reality as we know it. Herein, by making use of the three curved spacetime Dirac equations proposed in [2], we move the exercise of [1] from the realm of curiosity, speculation and chicanery to that of plausibility.
As already stated, in (1), it is not clear why the quantity “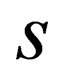 ” has to take integral values
” has to take integral values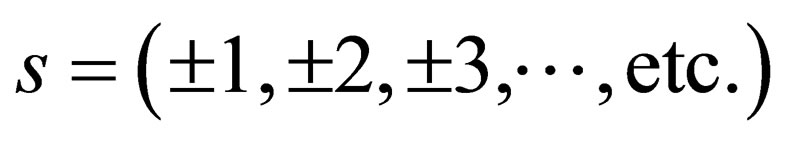 . Because spin has to take integral and half integral values, it was assumed without proof that this quantity “
. Because spin has to take integral and half integral values, it was assumed without proof that this quantity “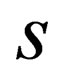 ” has to take integral values. This off cause is a hole in the theory that needs to be filled. This reading will furnish this missing part in the “General Spin Dirac Equation” proposed in [1]. We not only demonstrate how “
” has to take integral values. This off cause is a hole in the theory that needs to be filled. This reading will furnish this missing part in the “General Spin Dirac Equation” proposed in [1]. We not only demonstrate how “ ” comes to be part of the dispersion relation
” comes to be part of the dispersion relation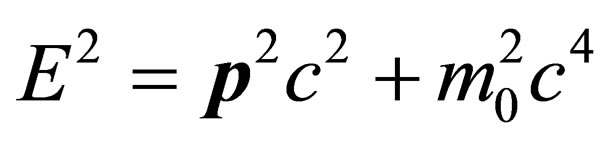 , but how and why this quantity comes to take only integer values.
, but how and why this quantity comes to take only integer values.
In summary, the aim or envisaged achievement(s) of the present work are threefold, i.e.:
1) We unambiguously demonstrate how the quantity “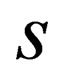 ” becomes a part of the Einstein energy-momentum dispersion relation.
” becomes a part of the Einstein energy-momentum dispersion relation.
2) We prove that “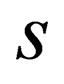 ” can only take integral values
” can only take integral values
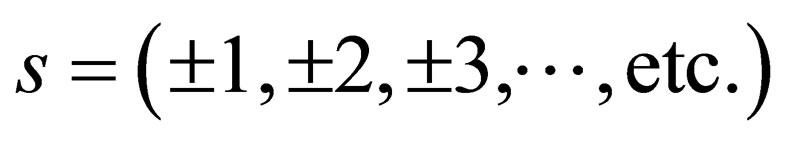 .
.
3) We generalise the notion of a “General Spin Dirac Equation” to include all the three curved spacetime Dirac equations [proposed in 2].
Now, in-closing this section, let us give a brief synopsis of the present reading. It is as follows. In the next section, we are going to give a brief exposition of the curved spacetime Dirac equation first presented in [2]. In the successive section, we are going to dwell on the main thrust of the present reading by demonstrating how “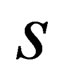 ” comes to be part of the dispersion relation
” comes to be part of the dispersion relation 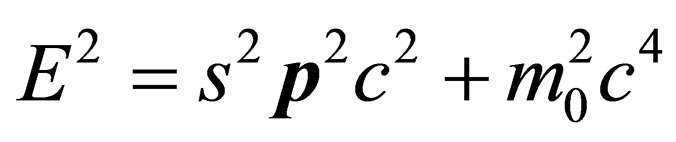 and as-well how and why “
and as-well how and why “ ” comes to take only integer values. Thereafter, we give a general discussion and the conclusions drawn thereof. Lastly, we are of the very strong view that any reader that wants or seeks to make sense of the present reading must first go through the readings [1,2] as these are minimum prerequisites. Otherwise, if they [the reader] do not do so, they will miss the main content and morass substance of the present reading.
” comes to take only integer values. Thereafter, we give a general discussion and the conclusions drawn thereof. Lastly, we are of the very strong view that any reader that wants or seeks to make sense of the present reading must first go through the readings [1,2] as these are minimum prerequisites. Otherwise, if they [the reader] do not do so, they will miss the main content and morass substance of the present reading.
2. Curved Spacetime Dirac Equations
As is well known, the Dirac equation is derived from the fundamental equation , where
, where 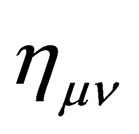 is the usual flat Minkowski metric with spacetime signature
is the usual flat Minkowski metric with spacetime signature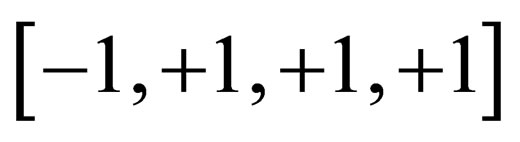 . We know that its equivalent in curved spacetime is given by:
. We know that its equivalent in curved spacetime is given by:
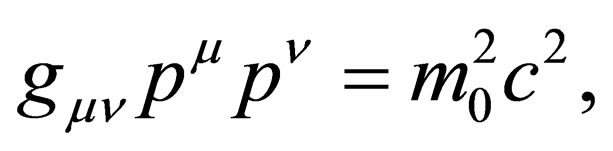 (3)
(3)
where the four momentum 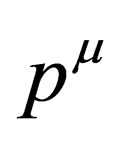 is given by
is given by  and
and 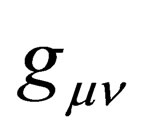 is the metric of spacetime. In order to aid the reader in visualizing (3) in a way that conforms to the end that we seek, we have to write this equation in its equivalent matrix form, i.e.:
is the metric of spacetime. In order to aid the reader in visualizing (3) in a way that conforms to the end that we seek, we have to write this equation in its equivalent matrix form, i.e.:
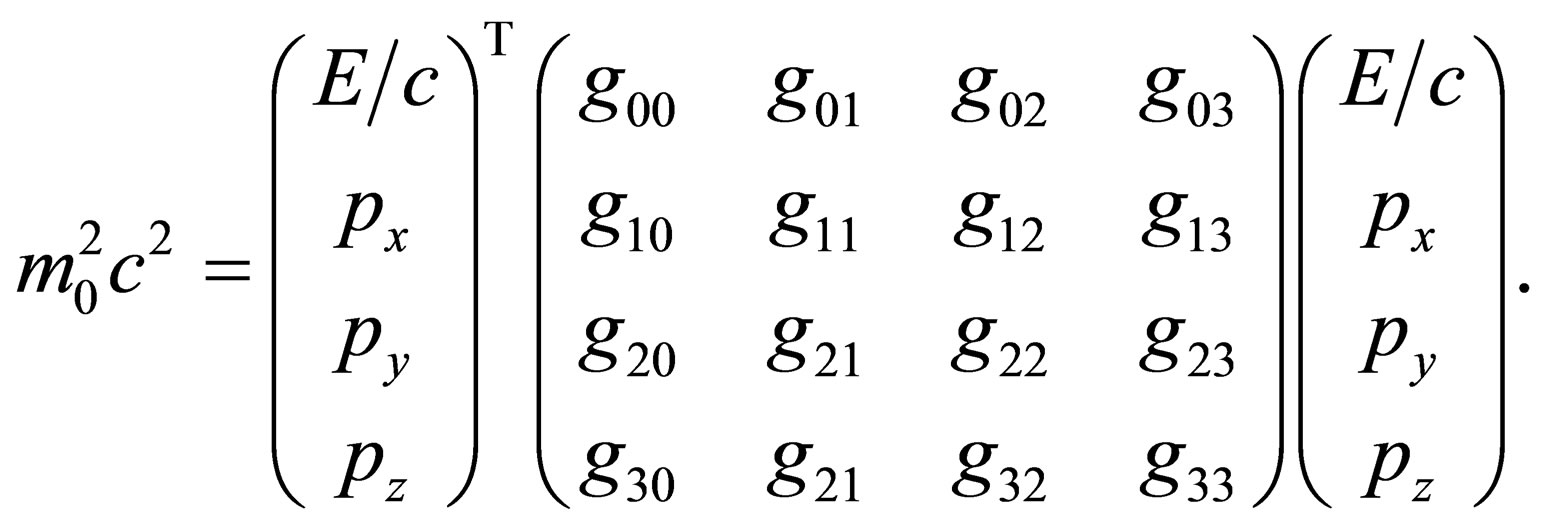 (4)
(4)
Above in (4), the “ ” in the superscript of the column vector denotes the transpose operation on that column vector.
” in the superscript of the column vector denotes the transpose operation on that column vector.
Now, in writing down the curved spacetime version of the Dirac equation [in the reading 2], we made a novel suggestion of writing down the spacetime metric tensor 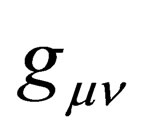 as:
as:
 (5)
(5)
where 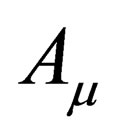 is some four vector and
is some four vector and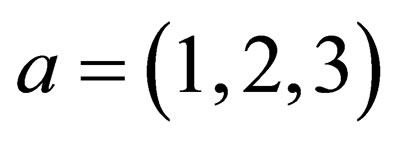 . In general, the metric
. In general, the metric 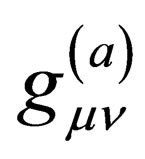 is such that:
is such that:
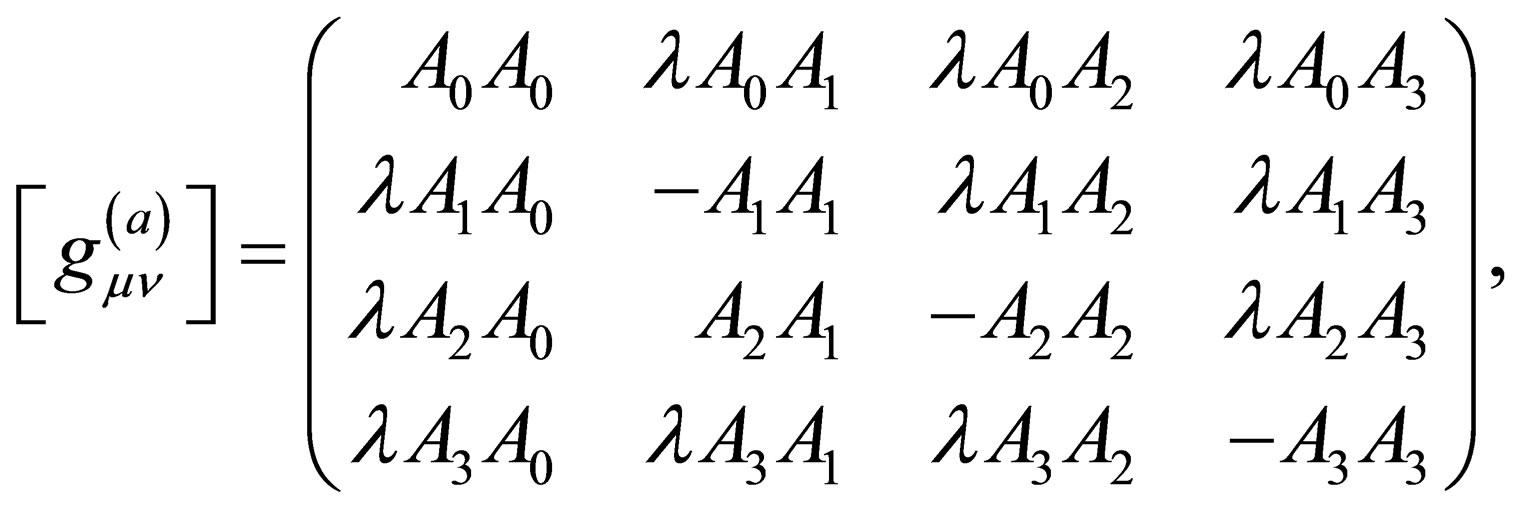 (6)
(6)
where for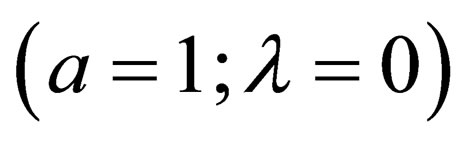 ,
,  and
and  . In the case
. In the case , there are no off-diagonal terms in the metric, while for the cases
, there are no off-diagonal terms in the metric, while for the cases , we have off diagonal terms [see 2]. As shown there in [2], the resulting three curved spacetime Dirac equations are given by:
, we have off diagonal terms [see 2]. As shown there in [2], the resulting three curved spacetime Dirac equations are given by:
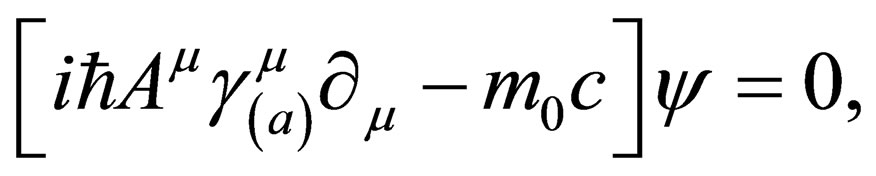 (7)
(7)
where2:
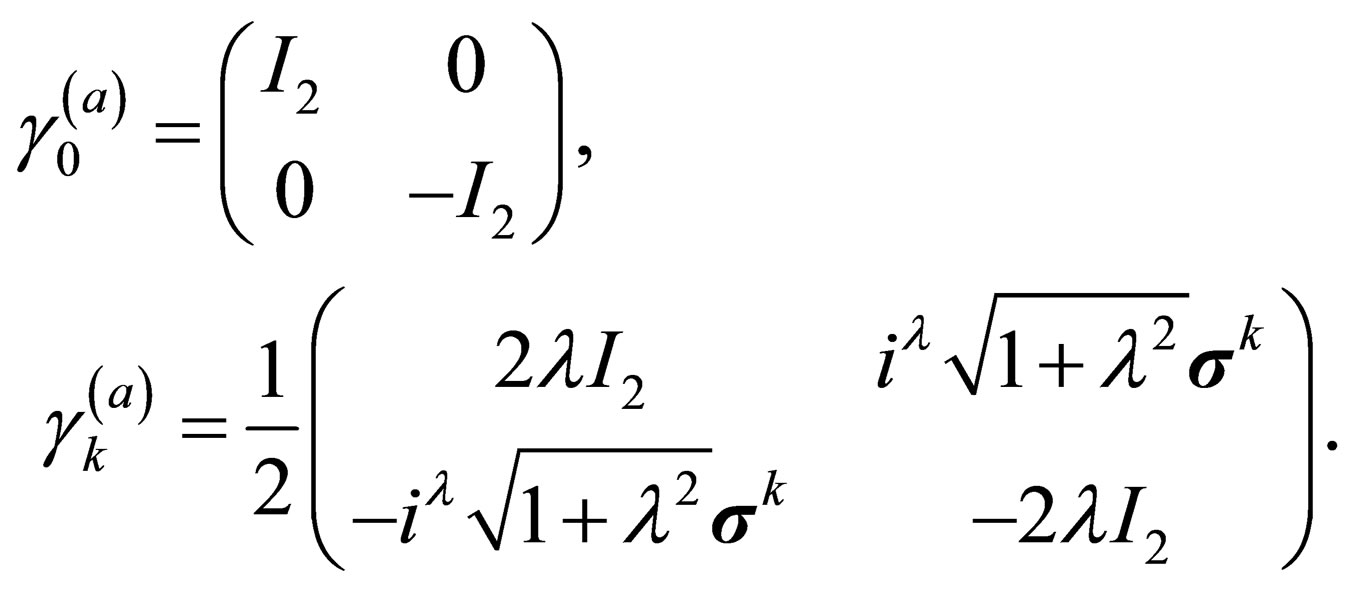 (8)
(8)
In the above (and hereafter), 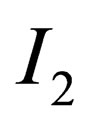 is the
is the 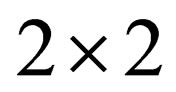 identity matrix,
identity matrix, 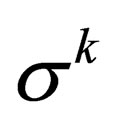 is the usual
is the usual 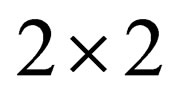 Pauli matrices and the
Pauli matrices and the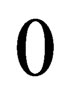 ’s are
’s are 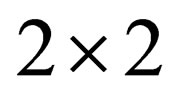 null matrices. It is not a difficult exercise to show that multiplication of (7) from the left handside by the operator
null matrices. It is not a difficult exercise to show that multiplication of (7) from the left handside by the operator 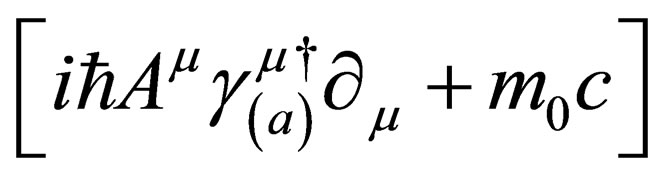 leads us to the curved spacetime Klein-Gordon equation
leads us to the curved spacetime Klein-Gordon equation 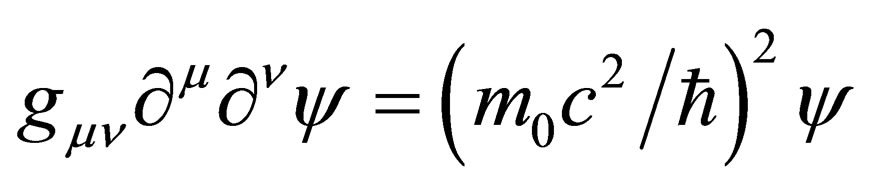 , provided
, provided . The condition
. The condition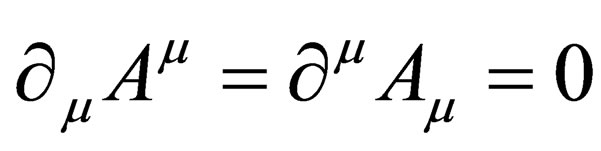 , should be taken as a gauge condition restricting this four vector. In the next section, we are going to demonstrate the Lorentz invariance of the curved spacetime Dirac equation (7).
, should be taken as a gauge condition restricting this four vector. In the next section, we are going to demonstrate the Lorentz invariance of the curved spacetime Dirac equation (7).
2.1. Lorentz Invariance
To prove Lorentz invariance3, two conditions must be satisfied, these two conditions are:
1) Given any two inertial observers  and
and 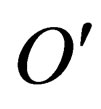 anywhere in spacetime, if in the frame
anywhere in spacetime, if in the frame 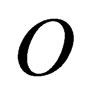 we have
we have
 then
then
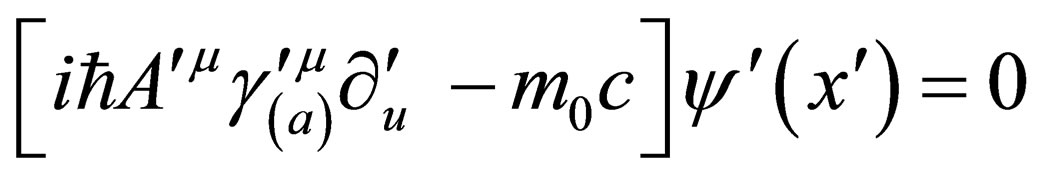
is the equation describing the same state but in the frame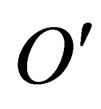 .
.
2) Given that 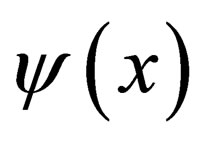 is the wavefunction as measured by observer
is the wavefunction as measured by observer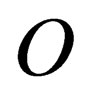 , there must be a prescription for observer
, there must be a prescription for observer 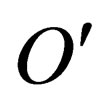 to compute
to compute 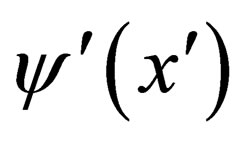 from
from 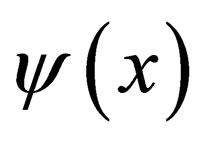 and this describes to
and this describes to 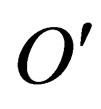 the same physical state as that measured by
the same physical state as that measured by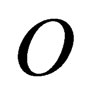 .
.
Now, since 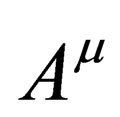 and
and 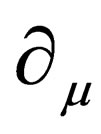 are both vectors, the quantity
are both vectors, the quantity 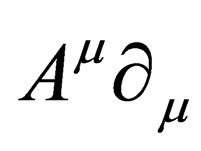 is obviously a scalar. From this, it follows that a Lorentz transformation is not going to affect
is obviously a scalar. From this, it follows that a Lorentz transformation is not going to affect 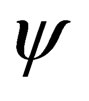 and
and 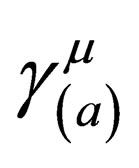 i.e.:
i.e.:
 (9)
(9)
The meaning of the above is that the matrices  are constant matrices and the Dirac four component
are constant matrices and the Dirac four component 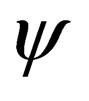 is represented in Case (I) where it is a scalar. The Dirac four component
is represented in Case (I) where it is a scalar. The Dirac four component 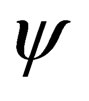 is not constrained to only be a scalar. In Case (II), we can have this transform under a multiplication of
is not constrained to only be a scalar. In Case (II), we can have this transform under a multiplication of 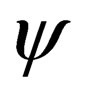 by some constant matrix
by some constant matrix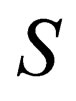 . If
. If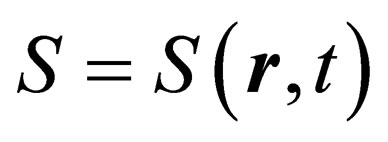 , then this matrix will have to be such that
, then this matrix will have to be such that  in-order for Lorentz invariance to hold.
in-order for Lorentz invariance to hold.
The present exercise to re-demonstrate the Lorentz invariance of (7) has been conducted so as to demonstrate the all-important difference that we must always take note of, that is, in the bare Dirac theory, the 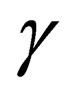 - matrices and as-well the four component function
- matrices and as-well the four component function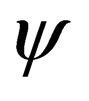 , do transform under a Lorentz transformation. This is not the case here;
, do transform under a Lorentz transformation. This is not the case here;  is a constant matrix and the Dirac four component function
is a constant matrix and the Dirac four component function 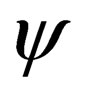 is scalar. In the reading [2], this very important fact that
is scalar. In the reading [2], this very important fact that 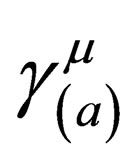 is a constant matrix and that the Dirac four component function
is a constant matrix and that the Dirac four component function 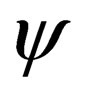 can be scalar, was missed altogether, hence the need to make this clear at the present moment in the further development of the curved spacetime Dirac equation.
can be scalar, was missed altogether, hence the need to make this clear at the present moment in the further development of the curved spacetime Dirac equation.
Additionally, we have shown here that Equation (7) is not Lorentz covariant but Lorentz invariant. The orginal Dirac equation is not Lorentz invariant but Lorentz convariant—this is something to be noted as it distinguishes the present effort from that of [3,4].
2.2. General Magnitude of a Four Vector
In this section, we are going to look into the issue of the magnitude of a four vector. For example, the square of the magnitude of the four momentum 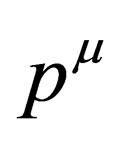 is such that
is such that . If we take a general four vector
. If we take a general four vector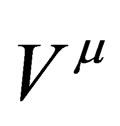 , then
, then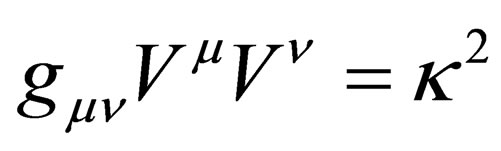 . Notice that in
. Notice that in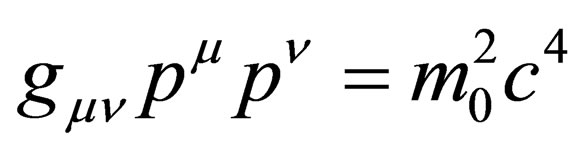 ,
, 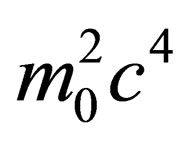 is a constant, it has the same value everywhere all the time; so that in general we can assume that the
is a constant, it has the same value everywhere all the time; so that in general we can assume that the  in
in , is a constant aswell. We ask, “In general, does
, is a constant aswell. We ask, “In general, does 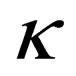 have to be a constant?” The answer to this question is a bold no! It only has to be a scalar since the quantity
have to be a constant?” The answer to this question is a bold no! It only has to be a scalar since the quantity 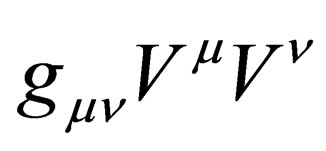 is a scalar. A constant is a special kind of a scalar, it is a scalar that takes the same value everywhere all the times. If
is a scalar. A constant is a special kind of a scalar, it is a scalar that takes the same value everywhere all the times. If 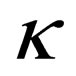 is a general scalar, then
is a general scalar, then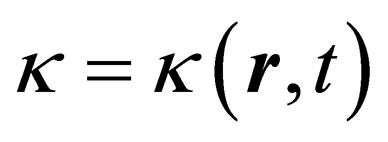 .
.
Given the above thesis i.e.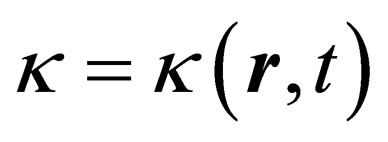 , what we seek here is a function that gives the value of
, what we seek here is a function that gives the value of  at the different
at the different  -points. Since
-points. Since 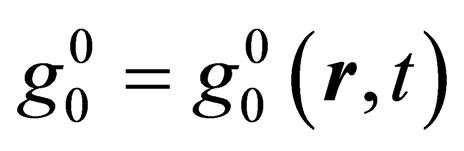 is itself a scalar, we propose that, in general, the magnitude of all four vectors in spacetime be such that
is itself a scalar, we propose that, in general, the magnitude of all four vectors in spacetime be such that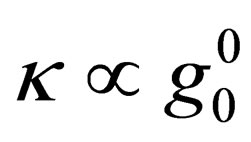 , so that:
, so that:
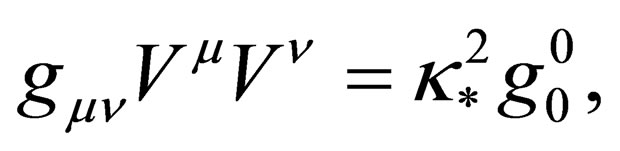 (10)
(10)
where  is a constant which takes the same value everywhere all the times for-all observers. The quantity
is a constant which takes the same value everywhere all the times for-all observers. The quantity  has the dimensions as that of
has the dimensions as that of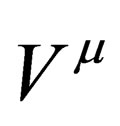 .
.
One may very well be tempted to ask the good question “What is the motivation for (10)?” Well—as will be seen in the next section; the motivation for the proposal (10) is that if we do not have such a setting, then contrary to experience, the rest mass of a particle in a curved spacetime will have to depend on where the particle is, and when it is at that place where it is— simple, . To avoid this, we have no choice but to impose (10).
. To avoid this, we have no choice but to impose (10).
2.3. Energy Solutions
The energy-momentum equation for the particles described by Equation (7) is:
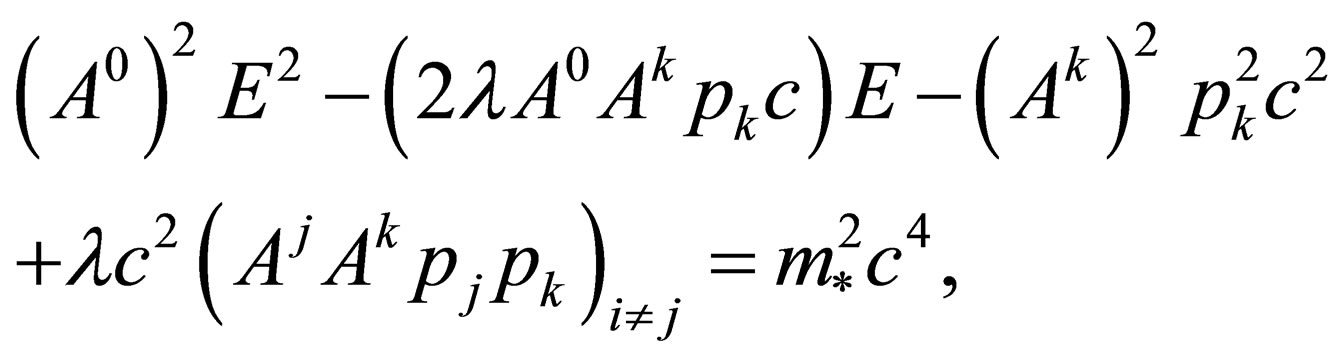 (11)
(11)
where in line with (10), we will have 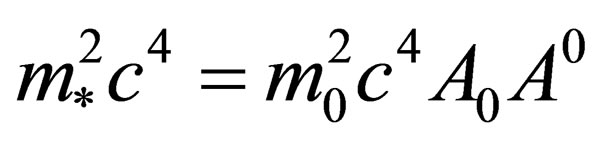
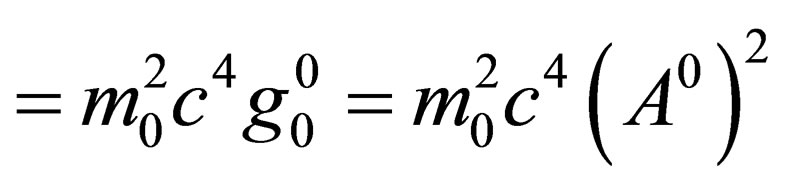 , where
, where  is a constant; and is the rest mass of the particle in question.
is a constant; and is the rest mass of the particle in question.
Now, dividing (11) throughout by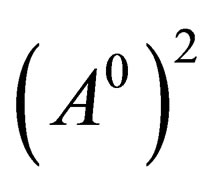 , we will have:
, we will have:
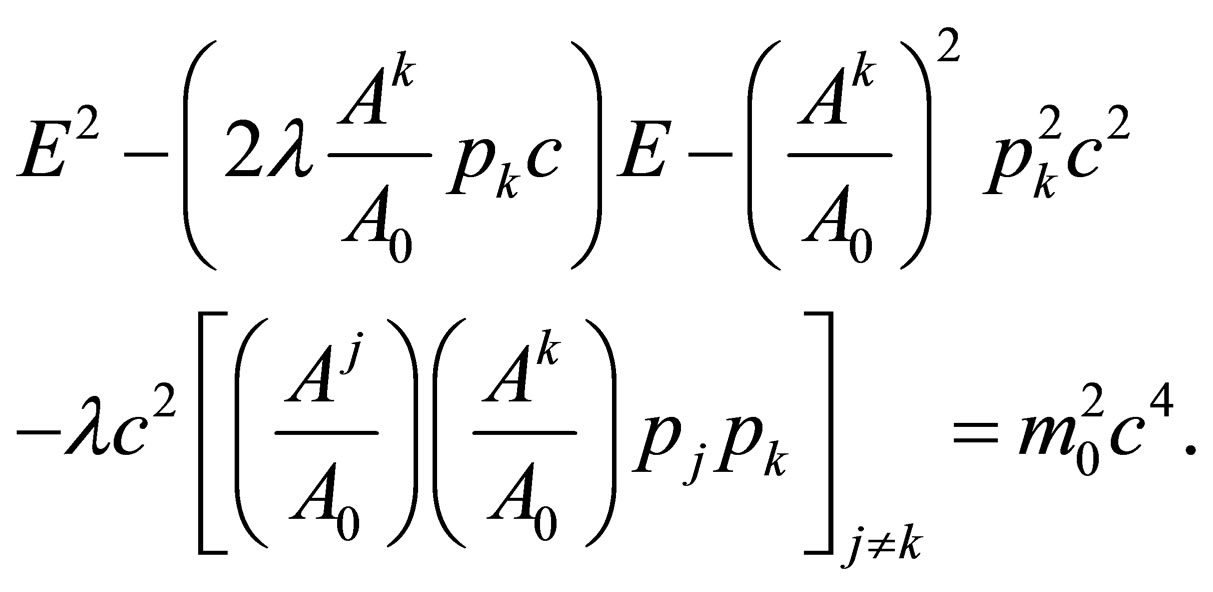 (12)
(12)
Notice that if  were a constant, then
were a constant, then

which goes against experience. It is for this reason that we afore-proposed the condition (10).
Now, setting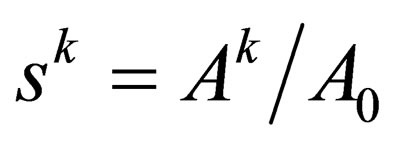 ; and inserting these settings into the above, we will have:
; and inserting these settings into the above, we will have:
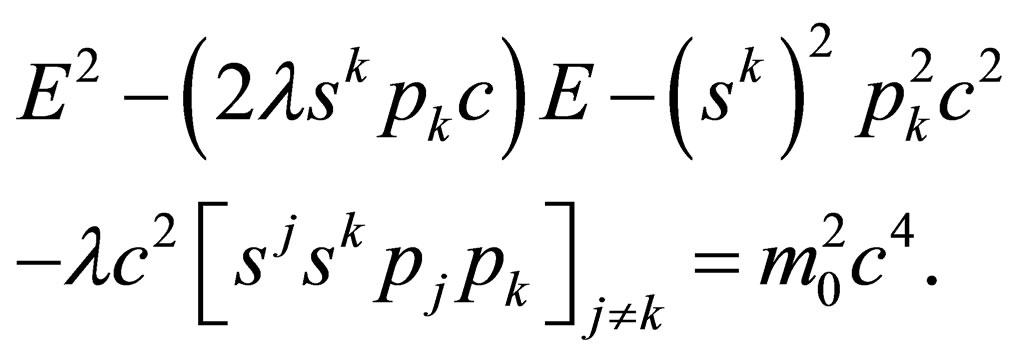 (13)
(13)
Making 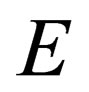 the subject of the formula, we will have:
the subject of the formula, we will have:
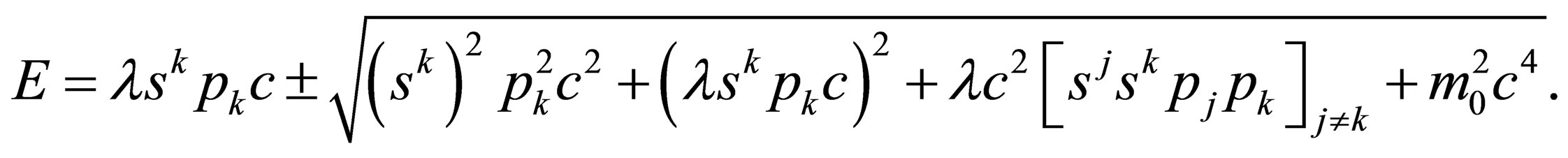 (14)
(14)
From this, it is clear that we will have three negative energy particles and three positive energy particles.
Now, in the next section, we are going to use (14) to justify the insertion of “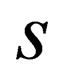 ” into the Einstein equation
” into the Einstein equation 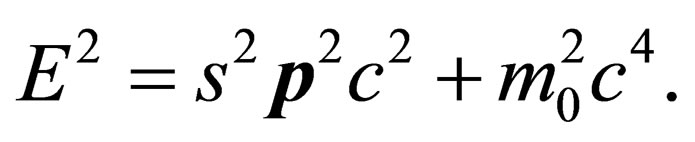 Note that the equation
Note that the equation 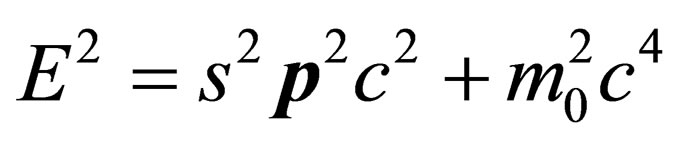 is in (14) the case for
is in (14) the case for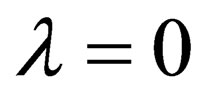 . Demonstrating how the “
. Demonstrating how the “ ” comes to be part of
” comes to be part of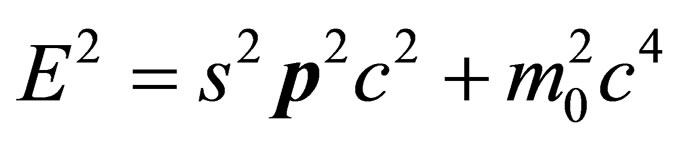 , also proves for the other cases
, also proves for the other cases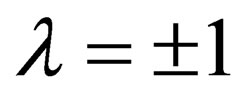 .
.
3. Justification
Let us consider the case . Space is usually assumed to be isotropic. This assumption finds solid justification form experience since observations reveal no directional properties of space, the deeper meaning of which is that space must have no preferential direction or directional properties. In the case of the metric (5), isotropy would mean that the space parts of the four vector
. Space is usually assumed to be isotropic. This assumption finds solid justification form experience since observations reveal no directional properties of space, the deeper meaning of which is that space must have no preferential direction or directional properties. In the case of the metric (5), isotropy would mean that the space parts of the four vector 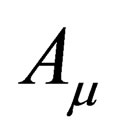 must all be equal or identical to each other, that is
must all be equal or identical to each other, that is 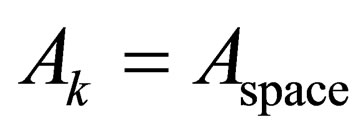 for-all
for-all . If this were the case that
. If this were the case that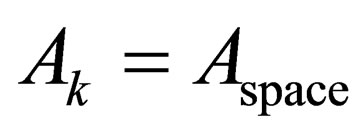 , then
, then 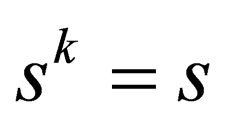 for-all
for-all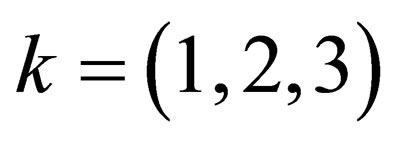 . From this, it follows that for the case
. From this, it follows that for the case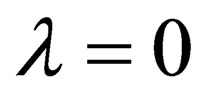 , we will have the energy-momentum equation:
, we will have the energy-momentum equation:
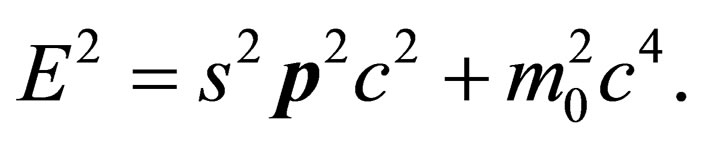 (15)
(15)
Thus, the equation 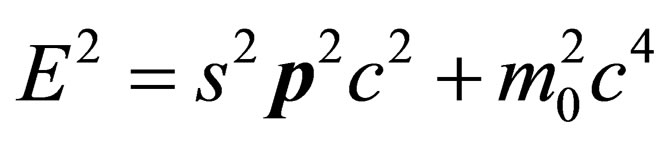 finds its sort for justification. What is left is to justify why and how “s” comes to take integral values
finds its sort for justification. What is left is to justify why and how “s” comes to take integral values 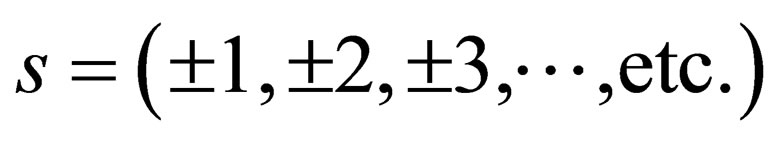 i.e. why and how
i.e. why and how  where
where  in the set of all positive and negative integers.
in the set of all positive and negative integers.
Before we go on to supply the above mentioned proof, let us write down the general spin dispersion relationship for a particle whose spacetime is isotropic. This we are going to do so that, we supply, not only the proof of why and how 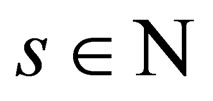 for the case
for the case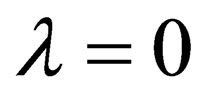 , but for the other two cases as-well i.e.
, but for the other two cases as-well i.e. . The general dispersion relationship of a particle whose spacetime is isotropic is given by:
. The general dispersion relationship of a particle whose spacetime is isotropic is given by:
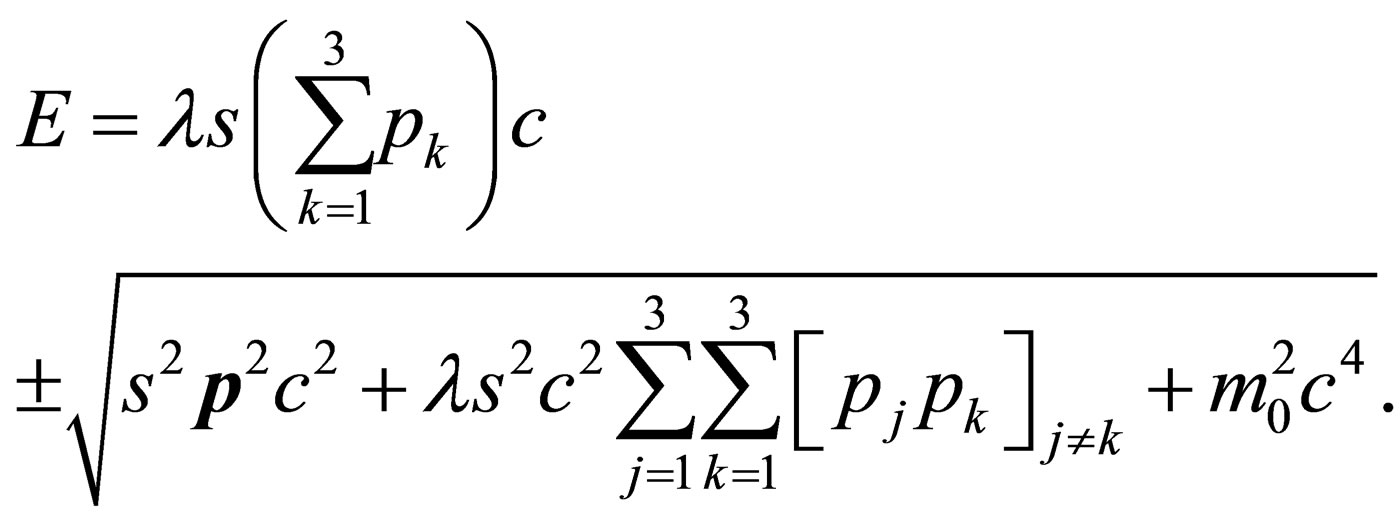 (16)
(16)
Now, (7) can be written in the general Schrödinger formulation as 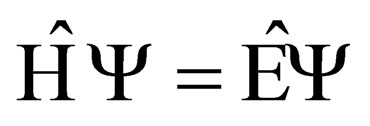 where
where  and
and  are the Hamiltonian and energy operators respectively. So doing, i.e. writing (7) in the said form, we will have:
are the Hamiltonian and energy operators respectively. So doing, i.e. writing (7) in the said form, we will have:
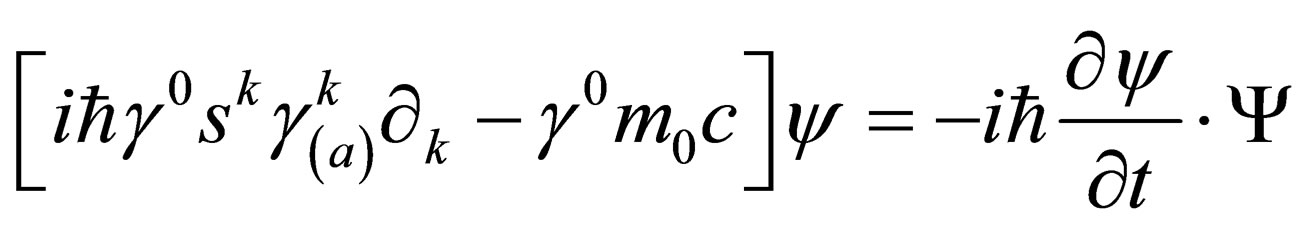 (17)
(17)
From this, it follows that the new General Spin Dirac Hamiltonian 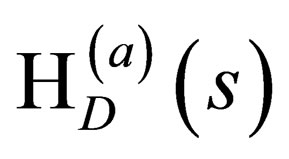 is given by:
is given by:
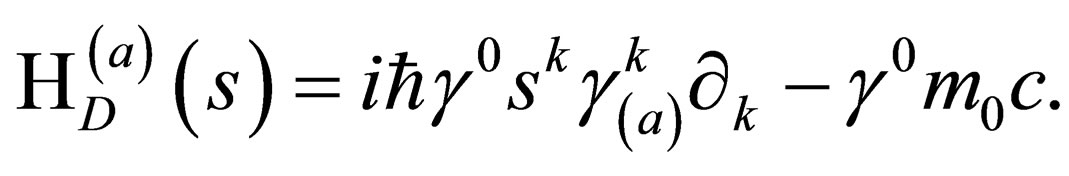 (18)
(18)
This General Spin Dirac Hamiltonian commutes with the total angular momentum operator 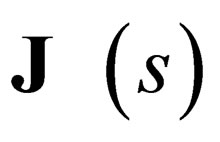 i.e.
i.e.
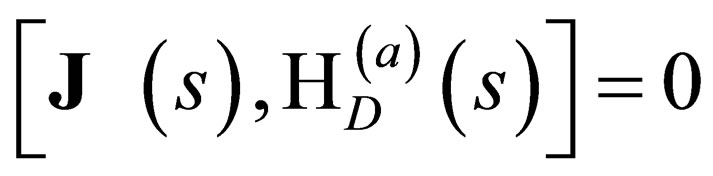 for-all
for-all 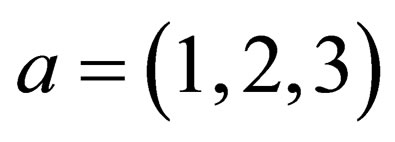 and for-all
and for-all
 . The proof of this assertion is supplied in the Appendix. This fact that
. The proof of this assertion is supplied in the Appendix. This fact that
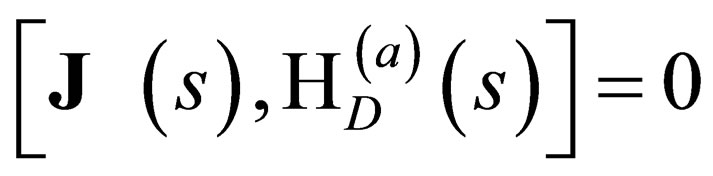 is important as it tells us that
is important as it tells us that
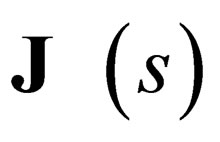 is the total angular momentum of the particle since it commutes with the Hamiltonian. The operator
is the total angular momentum of the particle since it commutes with the Hamiltonian. The operator 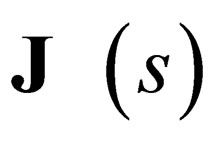 is such that:
is such that:
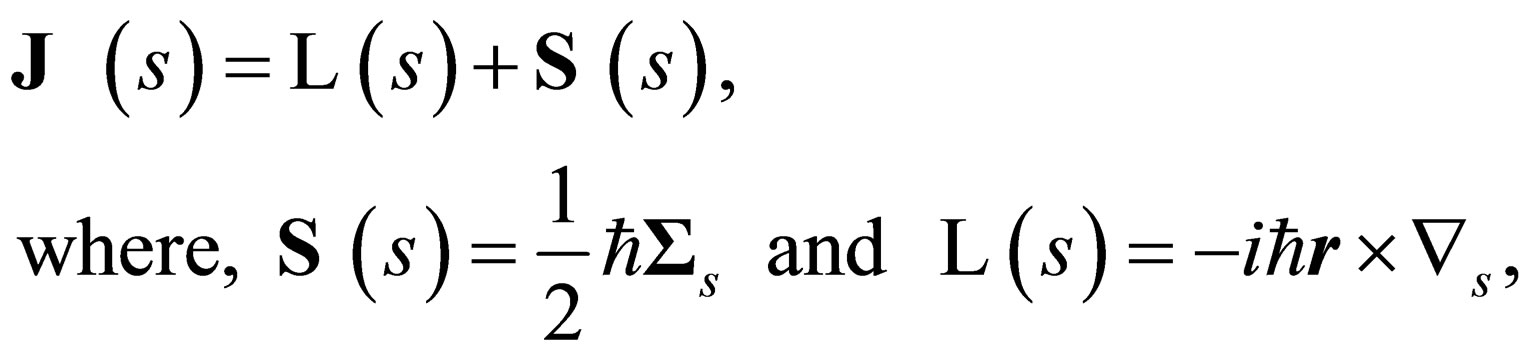 (19)
(19)
and as-well:
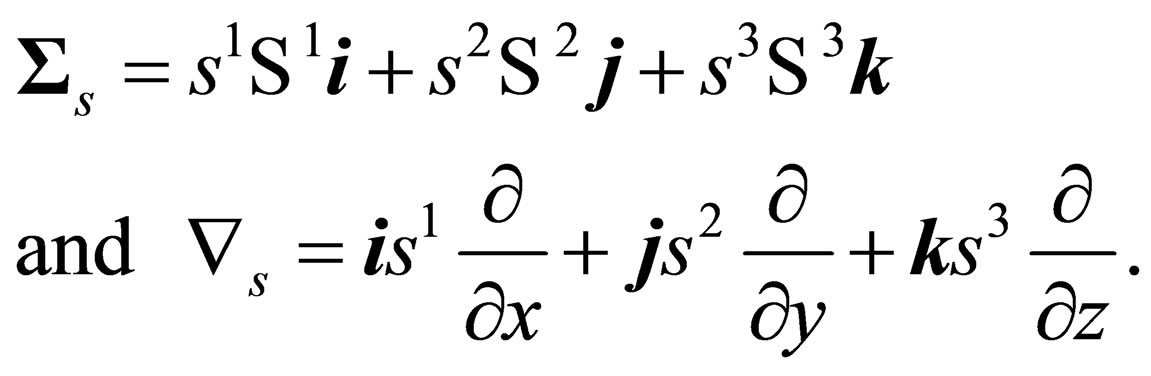 (20)
(20)
The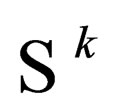 ’s are
’s are  matrices such that:
matrices such that:
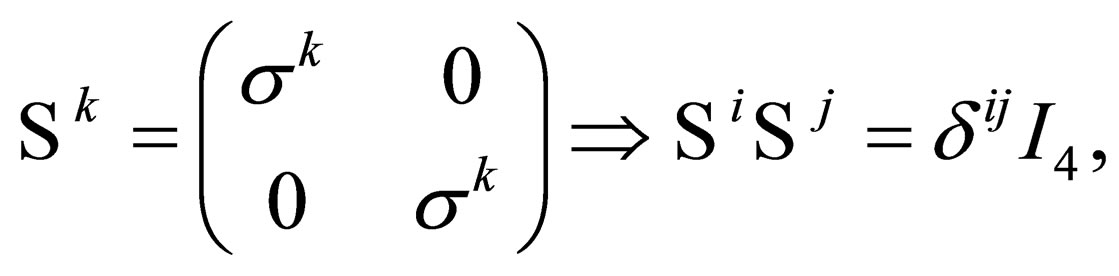 (21)
(21)
where  is the Kronecker-delta function which is such that
is the Kronecker-delta function which is such that 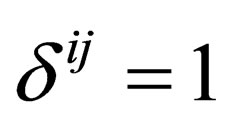 for
for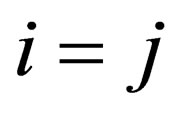 , and
, and 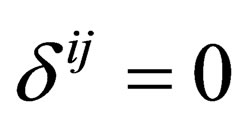 for
for 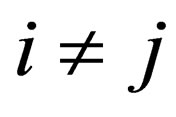 and
and 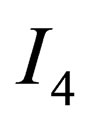 is (and hereafter) the
is (and hereafter) the  identity matrix. Clearly,
identity matrix. Clearly, 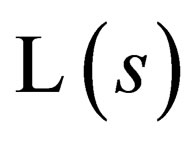 is the orbital angular momentum of the particle and likewise,
is the orbital angular momentum of the particle and likewise, 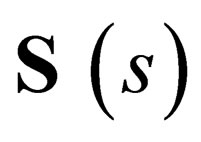 is the associated spin matrix.
is the associated spin matrix.
Now, to prove that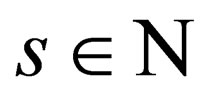 , as a first step, let us define the
, as a first step, let us define the  spin-operators:
spin-operators:
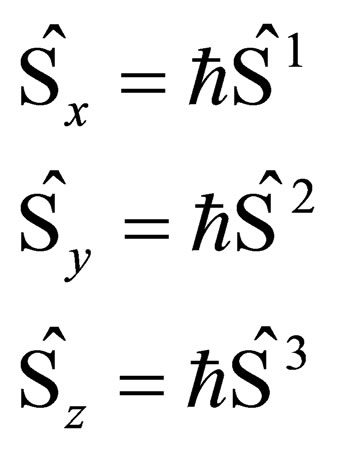 (22)
(22)
Further, let us define the  spin-ladder operators
spin-ladder operators 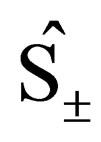 which are such that:
which are such that:
 (23)
(23)
In the above (and hereafter), 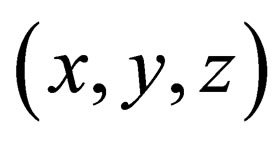 represent
represent 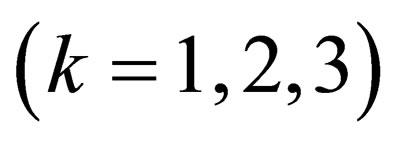 respectively. NB: hereafter, we shall without notice interchange the labels or indices i.e., sometimes we shall use
respectively. NB: hereafter, we shall without notice interchange the labels or indices i.e., sometimes we shall use 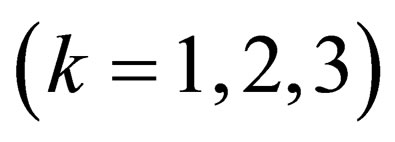 and sometimes
and sometimes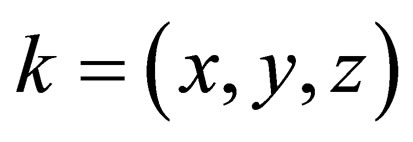 .
.
Now, these  spin-ladder operators are related to the operators
spin-ladder operators are related to the operators 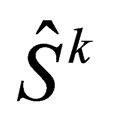 by the commutator relationship:
by the commutator relationship:
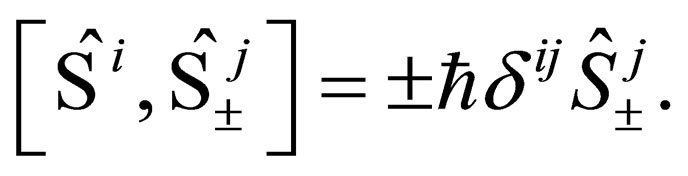 (24)
(24)
Now, we propose the following eigenvalue equation:
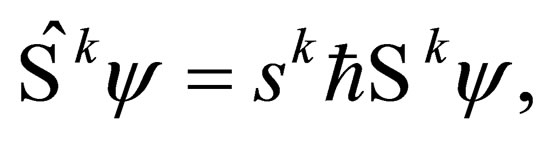 (25)
(25)
where 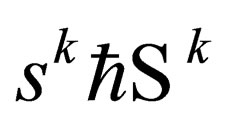 is the eigenvalue corresponding to the operator
is the eigenvalue corresponding to the operator 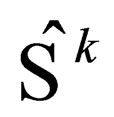 acting on
acting on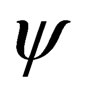 . How does such an eigenvalue equation come about? Well, in-order to have this eigenvalue equation, the operator
. How does such an eigenvalue equation come about? Well, in-order to have this eigenvalue equation, the operator  should be defined such that:
should be defined such that:
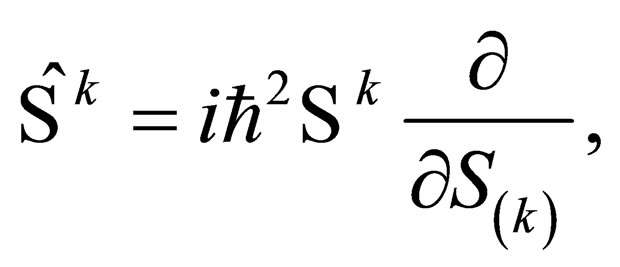 (26)
(26)
where 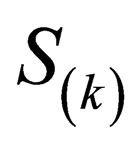 is the
is the 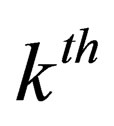 -component of the phase of the particle. That is, if
-component of the phase of the particle. That is, if 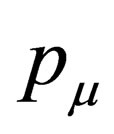 is the four momentum of a particle and
is the four momentum of a particle and 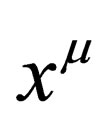 is its four position in spacetime, then, the phase of this particle
is its four position in spacetime, then, the phase of this particle  is such that
is such that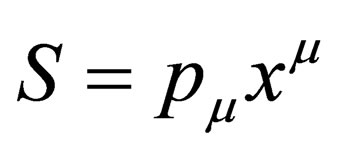 . This phase can be split into four components as
. This phase can be split into four components as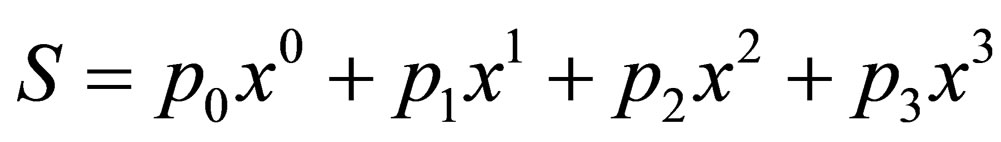 . The components
. The components 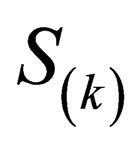 then are such that
then are such that 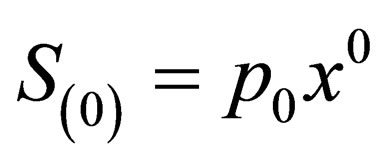 and
and ,
, 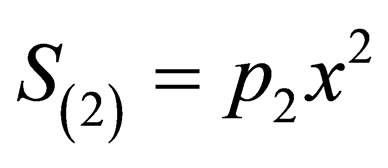 ,
, 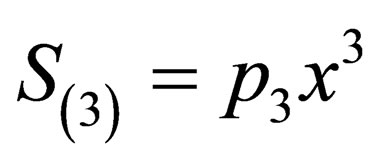 , so, we can write
, so, we can write 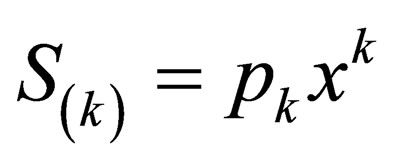 and the
and the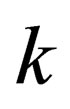 ’s are not summing up as is the case in the usual Einstein summation convention. Now, the wavefunction of any particle is a function of the phase, that is,
’s are not summing up as is the case in the usual Einstein summation convention. Now, the wavefunction of any particle is a function of the phase, that is,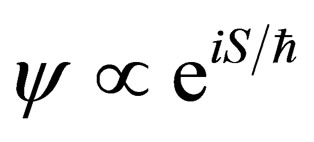 . Further, the phase of a curved spacetime Dirac particle is given by
. Further, the phase of a curved spacetime Dirac particle is given by 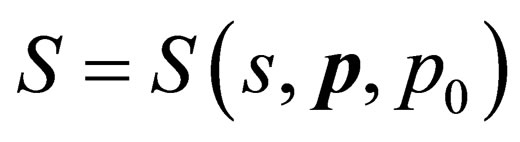
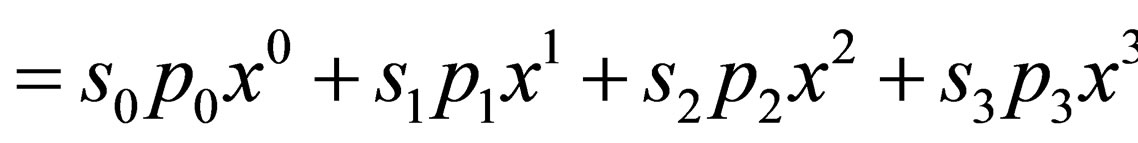 so that
so that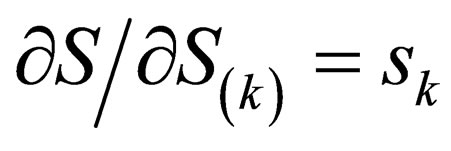 . With all this, it is now clear, how the eigenvalue Equation (25) arises or comes about.
. With all this, it is now clear, how the eigenvalue Equation (25) arises or comes about.
Now, multiplying (25) by  from the left, we will have
from the left, we will have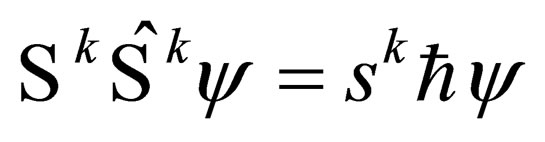 . From this, it follows that we can rewrite (1.17) as:
. From this, it follows that we can rewrite (1.17) as:
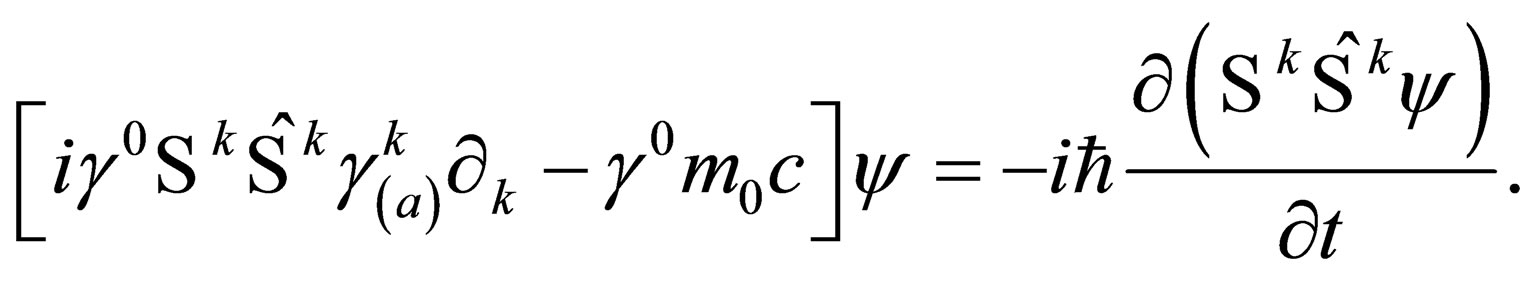 (27)
(27)
Acting on this equation from the left by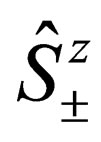 , one can easily show by using the fact (24), namely
, one can easily show by using the fact (24), namely
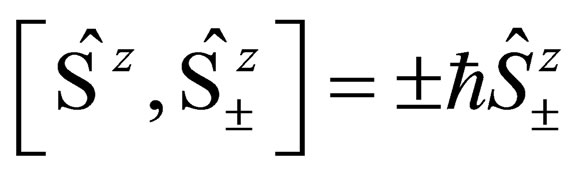 ,
,  for
for  and aswell the fact that
and aswell the fact that 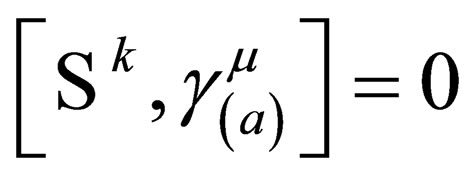 and
and , one arrives at the resulting equation:
, one arrives at the resulting equation:
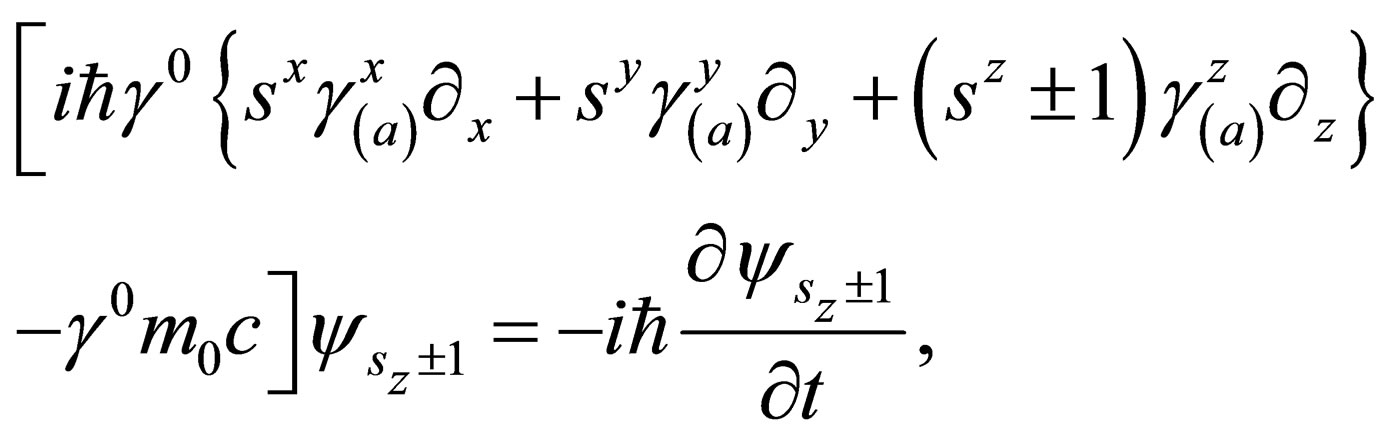 (28)
(28)
where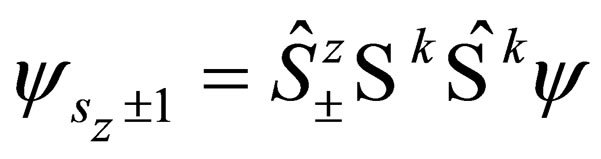 : in this equation i.e. (28)
: in this equation i.e. (28) 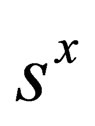 and
and 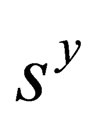 remain unchanged by the application of the operation
remain unchanged by the application of the operation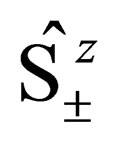 , while
, while 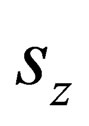 changes by one unit. The above equation describes a particle of spin
changes by one unit. The above equation describes a particle of spin 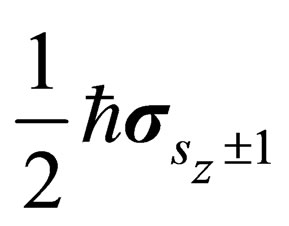
where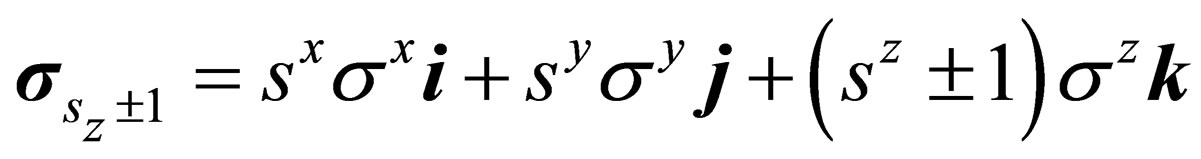 . The operator
. The operator 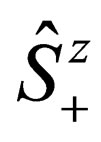 increases
increases 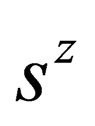 by one unit, while the operator
by one unit, while the operator 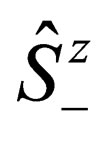 decreases this quantity by one unity. If we want to simultaneously raise or lower the spin for-all the
decreases this quantity by one unity. If we want to simultaneously raise or lower the spin for-all the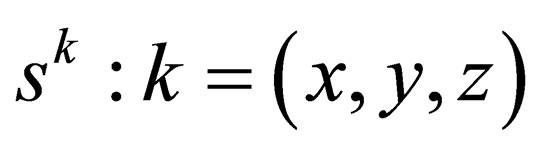 , then we have to act on (28) using all the three operators i.e.
, then we have to act on (28) using all the three operators i.e.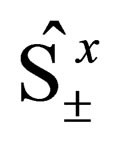 ,
, 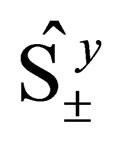 and
and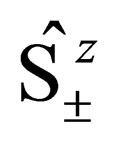 . This means we can define the operator:
. This means we can define the operator:
 (29)
(29)
which then acts on (28). That is, acting from the left on (28) using this new operator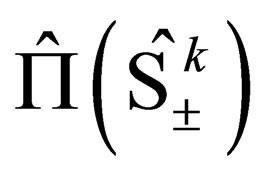 , and thereafter performing the necessary algebraic operations, the resulting equation is:
, and thereafter performing the necessary algebraic operations, the resulting equation is:
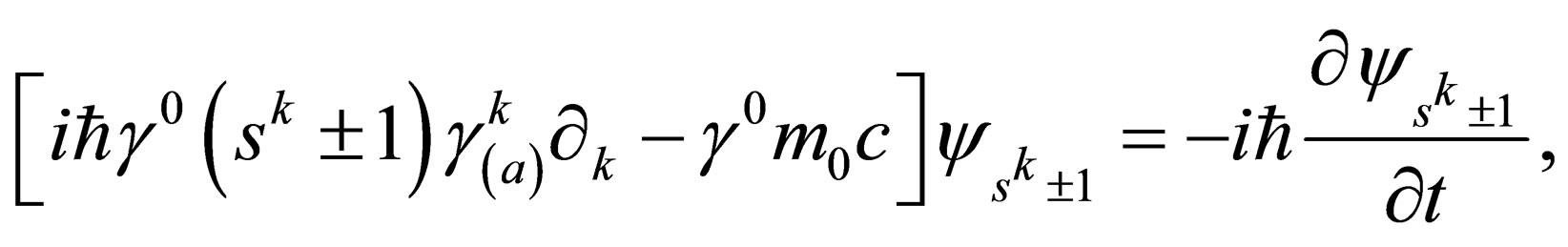 (30)
(30)
where , that is,
, that is, 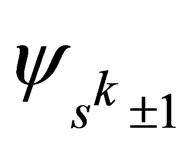 is the wavefunction of the particle
is the wavefunction of the particle 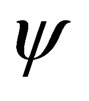 where the spin quantum
where the spin quantum  of
of 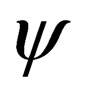 has either been increased
has either been increased 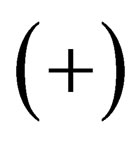 or decreased
or decreased 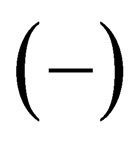 by one unit for-all the three directions
by one unit for-all the three directions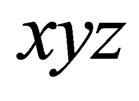 .
.
Now, to prove that “ ” only takes integral values, we simple have to prove that one of the values of “
” only takes integral values, we simple have to prove that one of the values of “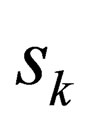 ” is an integer. Since “
” is an integer. Since “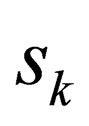 ” only changes by integral values, if just one of the values of “
” only changes by integral values, if just one of the values of “ ” is an integer, then, all the other values of this quantity must be integers too—surely, this is not difficult to understand. To prove that just one of the values of “
” is an integer, then, all the other values of this quantity must be integers too—surely, this is not difficult to understand. To prove that just one of the values of “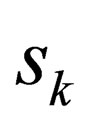 ” is an integer is not a difficult task to perform either. We know that in Minkowski spacetime where
” is an integer is not a difficult task to perform either. We know that in Minkowski spacetime where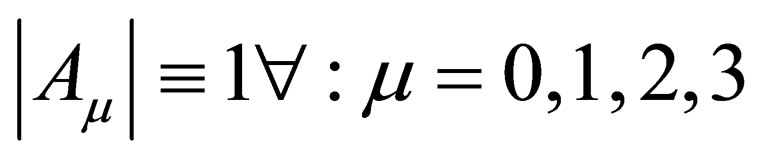 , the energy-momentum dispersion relation is given by the Einstein energy-momentum equation
, the energy-momentum dispersion relation is given by the Einstein energy-momentum equation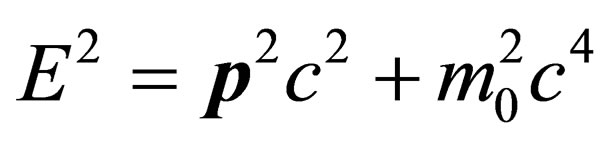 ; in this equation
; in this equation 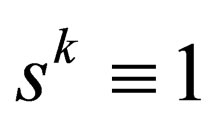 for-all
for-all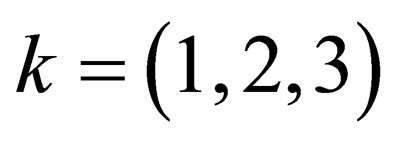 . If the Minkowski spacetime is envisaged as the lowest energy state for any quantum configuration, then
. If the Minkowski spacetime is envisaged as the lowest energy state for any quantum configuration, then  for-all
for-all 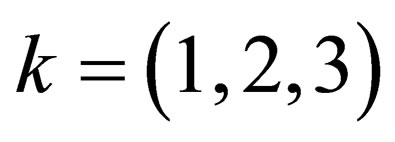 is one of the quantum mechanical states for any particle. Clearly, this is sufficient proof that one of the values of “
is one of the quantum mechanical states for any particle. Clearly, this is sufficient proof that one of the values of “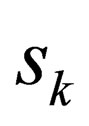 ” for-all
” for-all , is an integer. From the foregoing, it thus follows that “
, is an integer. From the foregoing, it thus follows that “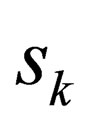 ” will take only integral values i.e.
” will take only integral values i.e. 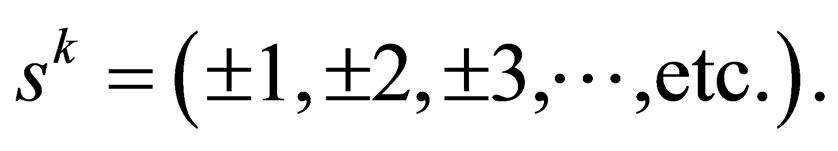 This completes the proof that
This completes the proof that 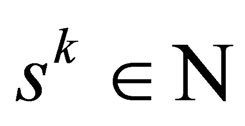 for-all
for-all . We have not only proved that “
. We have not only proved that “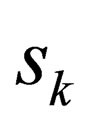 ” is an integer, but in so doing, we have also proved why spin is a quantised physical quantity.
” is an integer, but in so doing, we have also proved why spin is a quantised physical quantity.
4. Metric of a General Spin Dirac Particle
From the above findings, we can compute the general spacetime metric of a general spin Dirac particle. We have argued that the four vector 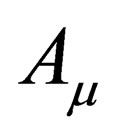 is such that
is such that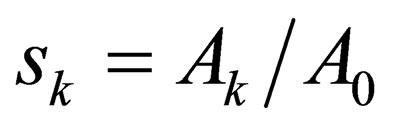 . From this, we can write down a four spin quantum number
. From this, we can write down a four spin quantum number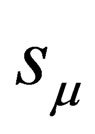 . To do this, we note that the four vector
. To do this, we note that the four vector 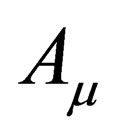 can be written with its components as
can be written with its components as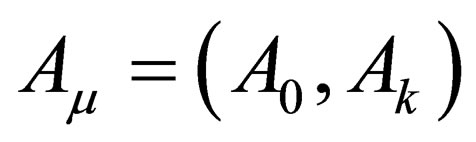 . Further, this can be written as
. Further, this can be written as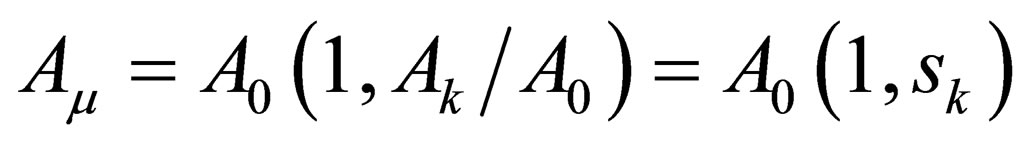 . The quantity
. The quantity  is the four spin quantum number that we seek i.e.,
is the four spin quantum number that we seek i.e., 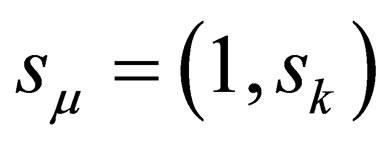 where
where . For our convenience, let us set
. For our convenience, let us set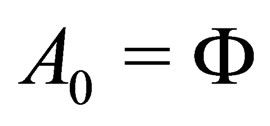 . From this, the four vector
. From this, the four vector 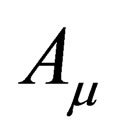 can now be written as
can now be written as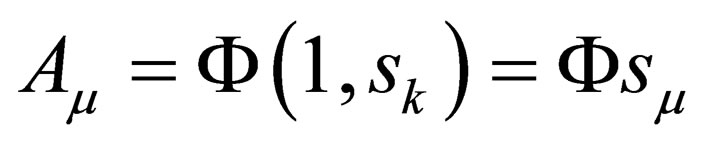 . Now, substituting
. Now, substituting 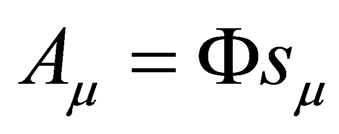 into (5), we will have:
into (5), we will have:
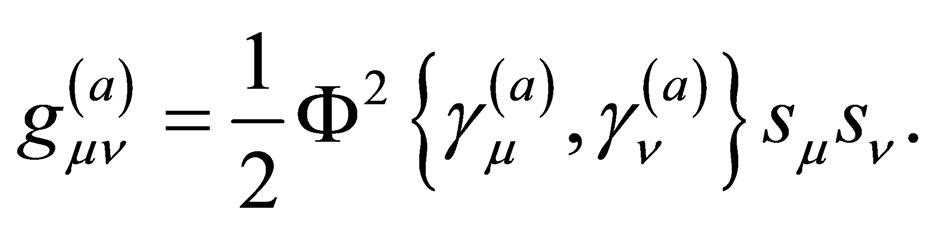 (31)
(31)
Written in full, 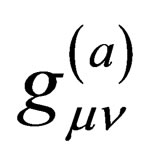 is such that:
is such that:
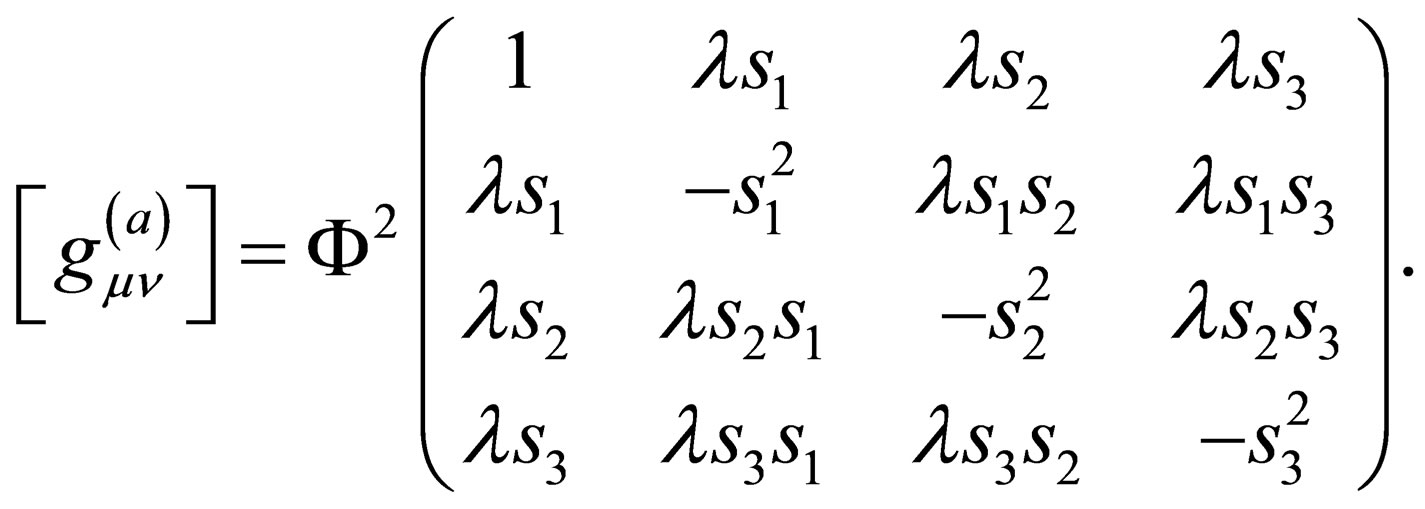 (32)
(32)
From this, we see that the metric is controlled by one variable function 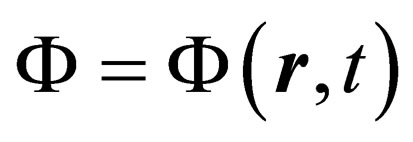 since
since 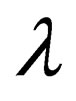 and
and 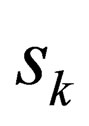 are all constants. Thus, (32) is the metric of a general spin curved spacetime Dirac particle.
are all constants. Thus, (32) is the metric of a general spin curved spacetime Dirac particle.
The usual metric of spacetime  has ten potentials. This was reduced to four potential by the introduction of the four vector
has ten potentials. This was reduced to four potential by the introduction of the four vector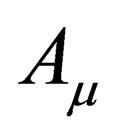 . Now, these four potentials have been reduced to just one potential. This is a tremendous simplification—from ten potentials to just one potential! At this point, the reader may legitimately want to ask if
. Now, these four potentials have been reduced to just one potential. This is a tremendous simplification—from ten potentials to just one potential! At this point, the reader may legitimately want to ask if 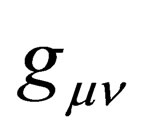 has the same meaning as in Einstein’s General Theory of Relativity (GTR)? To answer this question, one has to visit the reading [5]. It is shown there in [5] that the vector
has the same meaning as in Einstein’s General Theory of Relativity (GTR)? To answer this question, one has to visit the reading [5]. It is shown there in [5] that the vector 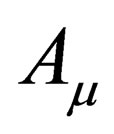 gives raise to the nuclear force nonabelian gauge field. The details of the Unified Field Theory presented in [5] are still being worked out. What the reader can do for now is simple take
gives raise to the nuclear force nonabelian gauge field. The details of the Unified Field Theory presented in [5] are still being worked out. What the reader can do for now is simple take 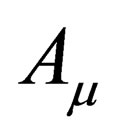 as a four vector and nothing else. As to whether this vector represents a gravitational, electric or any force field for that matter is of no consequence here since we are not concerned with the force field which this four vector represents.
as a four vector and nothing else. As to whether this vector represents a gravitational, electric or any force field for that matter is of no consequence here since we are not concerned with the force field which this four vector represents.
5. Discussion and Conclusion
We strongly believe that this reading justifies the assertion made in [1], namely that the modified Einstein dispersion relation 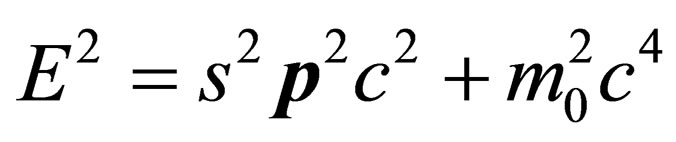 leads to a general spin Dirac equation. When this assertion was made in [1], it was not clear then, as to how such a dispersion relation would arise in Nature. We have shown that the curved spacetime Dirac equation proposed in [2] can be used to justify the modified Einstein dispersion relation
leads to a general spin Dirac equation. When this assertion was made in [1], it was not clear then, as to how such a dispersion relation would arise in Nature. We have shown that the curved spacetime Dirac equation proposed in [2] can be used to justify the modified Einstein dispersion relation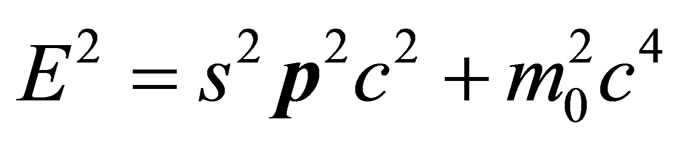 . Not only have we justified this, we have also argued that “
. Not only have we justified this, we have also argued that “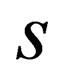 ” must take integral values. This means that, the work presented in [1] has been put on a much more acceptable pedestal. The reason we say this is because we believe that despited the fact that the true meaning and significance the curved spacetime Dirac equation derived in [2] has not been found yet, these curved spacetime Dirac equations are credible, mathematically and physically legitimate equations. Actually, it has been demonstrated that these curved spacetime Dirac equation are key to the attainment of a general spin Dirac equation.
” must take integral values. This means that, the work presented in [1] has been put on a much more acceptable pedestal. The reason we say this is because we believe that despited the fact that the true meaning and significance the curved spacetime Dirac equation derived in [2] has not been found yet, these curved spacetime Dirac equations are credible, mathematically and physically legitimate equations. Actually, it has been demonstrated that these curved spacetime Dirac equation are key to the attainment of a general spin Dirac equation.
Insofar as the unification programme of physics is concerned, we believe that the writing down of an acceptable general spin Dirac equation is a step in the right direction. If discovered, the final unified theory is expected to be such that a “single equation/principle will explain about every observable phenomenon. Amongst others, it is expected that a single equation must be able to explain all particles from a simple unifying principle. In the light of the aforestated, it is somewhat sad to say that the current state of physics vis the equations purporting to explain particles—is very “ugly”. For example, the Schrödinger equation describes spin-0 atoms and molecules [6], the Klein-Gordon equation describes spin-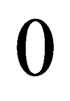 particles (that is carriers of forces), while the Dirac equation describes spin-1/2 particles, and the Rarita-Schwinger equation describes spin-3/2 particles [7]. From this rather “ugly” trend, does it mean we have to look for another equation to describe spin-2 particles, and then another for spin-5/2 particles etc? This does not look beautiful, simple, or at the very least suggest at the far and deeper end, a unification of the Natural Laws. It is on this note that we feel the present endeavours are worthwhile.
particles (that is carriers of forces), while the Dirac equation describes spin-1/2 particles, and the Rarita-Schwinger equation describes spin-3/2 particles [7]. From this rather “ugly” trend, does it mean we have to look for another equation to describe spin-2 particles, and then another for spin-5/2 particles etc? This does not look beautiful, simple, or at the very least suggest at the far and deeper end, a unification of the Natural Laws. It is on this note that we feel the present endeavours are worthwhile.
Another interesting outcome is that (7) is no longer restricted to the description of Fermions, but Bosons aswell. If this equation proves successful as happened with Dirac’s original equation, then, it will perhaps be the first equation in physics to describe both Fermions and Bosons from a single unified principle or standpoint. Further, this equation shares some common ground with super-symmetry theories—that is, theories that try and unify quantum mechanics and gravitation; in that it allows for the transmutation of a Fermion to a Boson and vice-versa. We believe this equation might very well be of interest to physicists working in this field. To transform a Fermion to a Boson and vice-versa, one simple acts on the wavefunction 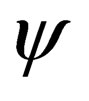 with the operator
with the operator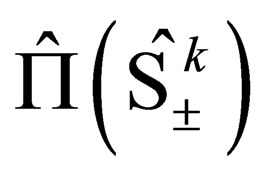 . In physical terms, we have no idea what an operation on
. In physical terms, we have no idea what an operation on 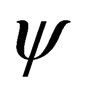 with
with 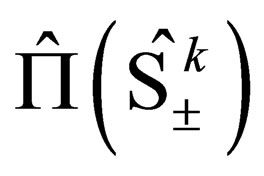 is. For all we know is that from an abstract mathematical standpoint, this is what one must do. Our hope is that these and other seemingly strange concepts and operations will become clear as horizons of our insight deepens.
is. For all we know is that from an abstract mathematical standpoint, this is what one must do. Our hope is that these and other seemingly strange concepts and operations will become clear as horizons of our insight deepens.
In-closing, we would like to point out something of note that we have not made mention of, namely that, the writing down of the general spin Dirac Equations (30) has brought about a great simplification of the three curved spacetime Dirac Equations (7). When these equations were first written down [in 2], we wondered if they would be soluble at all. To dramatise and express this feeling, this reading [2] was started with a quote from Paul Dirac, namely:
“The underlying Physical Laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these Laws leads to equations much too complicated to be soluble”.
The apparent insolubility is because of the presence of four vector  in Equation (7). Our guess then was that (7) would need to be solved numerically in-order to solve for
in Equation (7). Our guess then was that (7) would need to be solved numerically in-order to solve for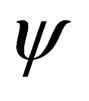 , but the present effort has unequivocally shown that this is not the case since
, but the present effort has unequivocally shown that this is not the case since  has been shown to take integer values thus literally eliminating what appeared to be a sure and impending mathematical nightmare of a numerical solution of the
has been shown to take integer values thus literally eliminating what appeared to be a sure and impending mathematical nightmare of a numerical solution of the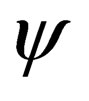 .
.
Conclusion
Assuming the acceptability (correctness) of the ideas propagated herein, we hereby make the following conclusions:
1) We have demonstrated that the curved spacetime Dirac equations [presented in Ref. 2] naturally lead to a general spin Dirac equation.
2) The spin of these curved spacetime Dirac particles is found to be naturally quantised i.e. it comes in integral multiples of a fundamental basic unit of spin. This spin quantization strongly appears to be wholly a part and parcel of the fabric of spacetime itself.
3) The fact that the spin of a particle is measured to be the same independent of the orientation; this fact suggests very strongly that spacetime must be isotropic on a quantum scale. If this were not the case that space is isotropic on the quantum scale, then, according to the ideas propagated herein, a particles’ spin will be different when measured in different random directions.
4) It has been shown that the curved spacetime Dirac equation leads to a Dirac wavefunction that can take a scalar nature, i.e., the resulting four component wavefunction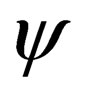 , together with the
, together with the 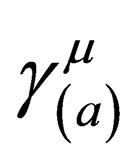 matrices; there are not affected by a Lorentz transformation. Effectively, the resulting curved spacetime Dirac equation is not Lorentz covariant, but truly Lorentz invariant in the true sense of Lorentz invariance.
matrices; there are not affected by a Lorentz transformation. Effectively, the resulting curved spacetime Dirac equation is not Lorentz covariant, but truly Lorentz invariant in the true sense of Lorentz invariance.
6. Acknowledgements
I am grateful to the various anonymous Reviewers for their effort that greatly improved and refined the arguments presented herein. Further, I am grateful to the National University of Science and Technology’s Research & Innovation Department and Research Board for their unremitting support rendered toward my research endeavours; of particular mention, Dr. P. Makoni and Prof. Y. S. Naik’s unwavering support. This publication proudly acknowledges a GRANT from the National University of Science and Technology’s Research Board.
REFERENCES
- G. G. Nyambuya, Apeiron, Vol. 16, 2009, pp. 516-531.
- G. G. Nyambuya, Foundations of Physics, Vol. 38, 2008, pp. 665-677.
- P. A. M. Dirac, Proceedings of the Royal Society B: Biological Sciences, Vol. A117, 1928, pp. 610-612.
- P. A. M. Dirac, Proceedings of the Royal Society B: Biological Sciences, Vol. A118, 1928, pp. 351-361.
- G. G. Nyambuya, “Toward Einstein’s Dream—On a Generalized Theory of Relativity,” LAP LAMBERT Academic Publishing, 2010.
- E. Schrödinger, Physical Review, Vol. 28, 1926, pp. 1049-1070. doi:10.1103/PhysRev.28.1049
- W. Ratita and J. Schwinger, Physical Review, Vol. 60, 1941, p. 61. doi:10.1103/PhysRev.60.61
Appendix
We are going to prove the crucial assertion that we stated on page (2022) without any proof, namely that:
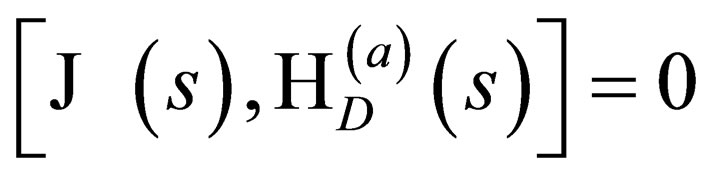 for-all
for-all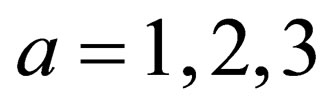 . To begin, we know that:
. To begin, we know that:
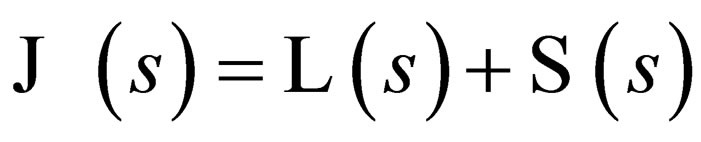 from this and as-well from the fact that:
from this and as-well from the fact that:
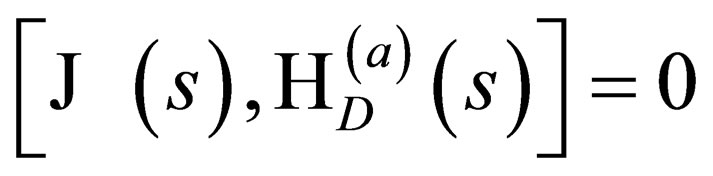 it follows that:
it follows that:
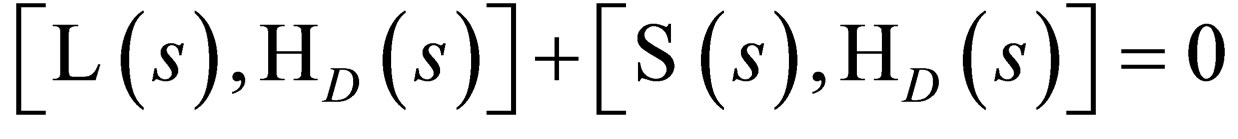 .
.
We also know that:
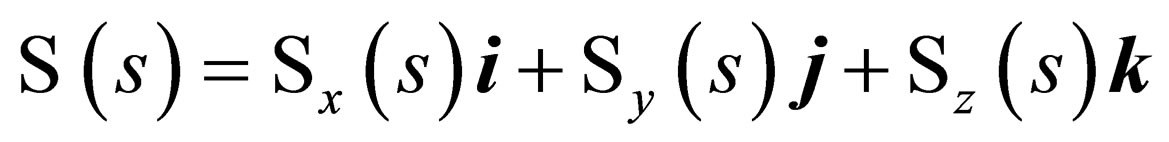
and
 ;
;
combining these facts, one obtains that:
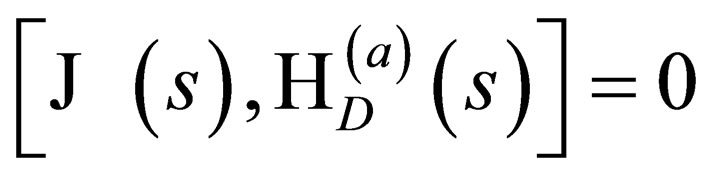 , (A.1)
, (A.1)
where  and
and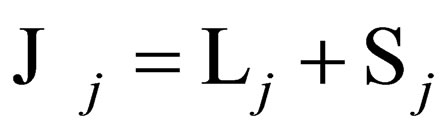 . So, if we can prove (A.1) for-all
. So, if we can prove (A.1) for-all  and for-all
and for-all , we will have proved that
, we will have proved that  for-all
for-all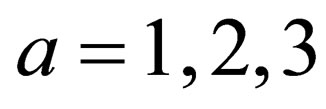 . We only have to prove this for just one of the three cases
. We only have to prove this for just one of the three cases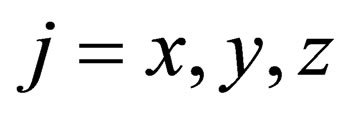 , this prove is sufficient as prove for the remaining two cases. We shall prove this for the case
, this prove is sufficient as prove for the remaining two cases. We shall prove this for the case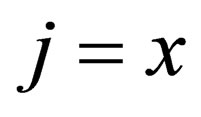 . We know that:
. We know that:
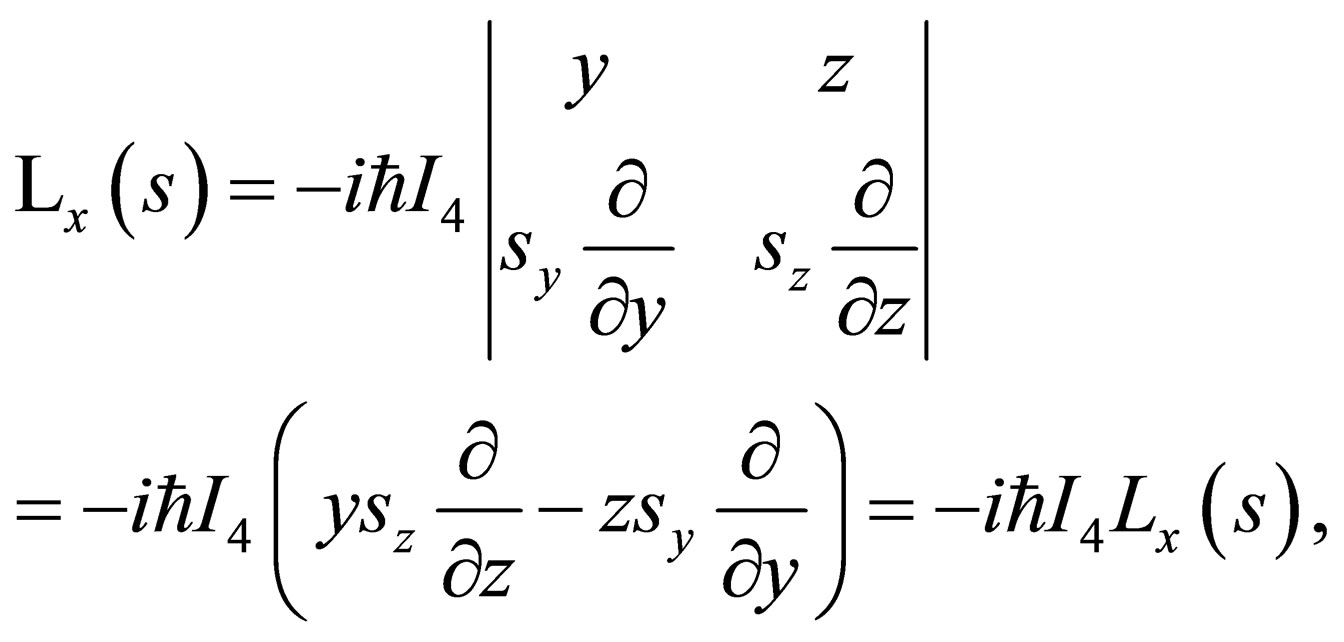 (A.2)
(A.2)
where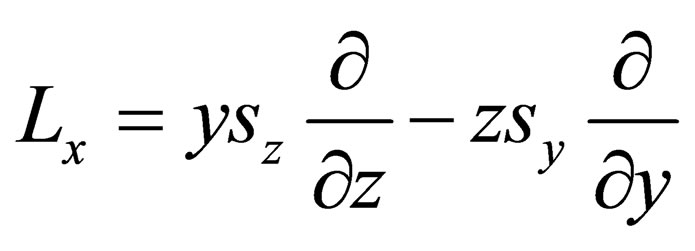 . From this, it follows that:
. From this, it follows that:
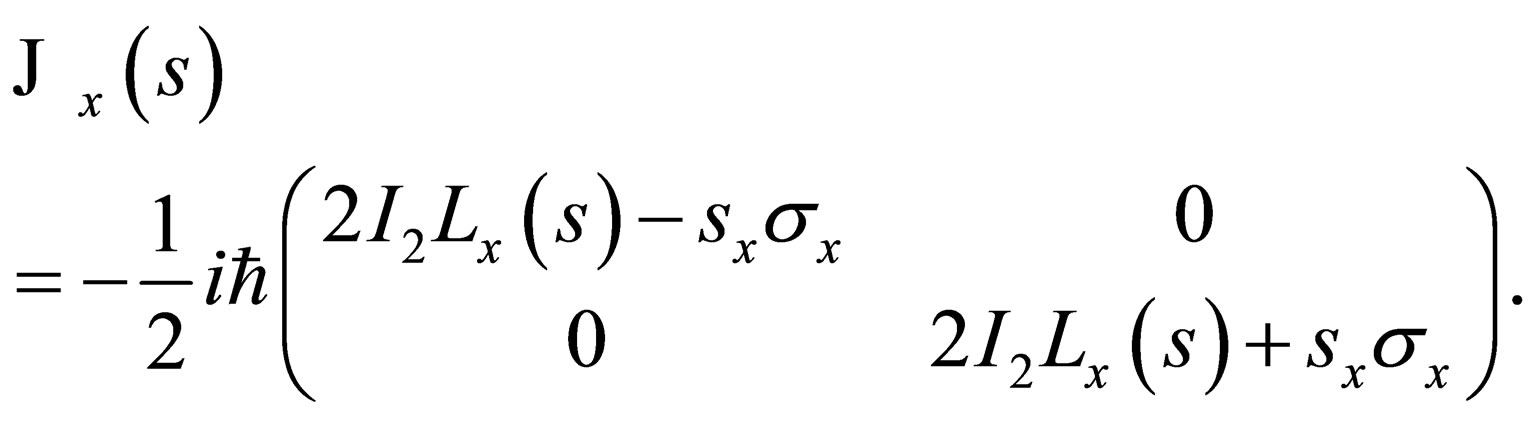 (A.3)
(A.3)
Now, since , (A.1) implies that for the case
, (A.1) implies that for the case , we will have:
, we will have:
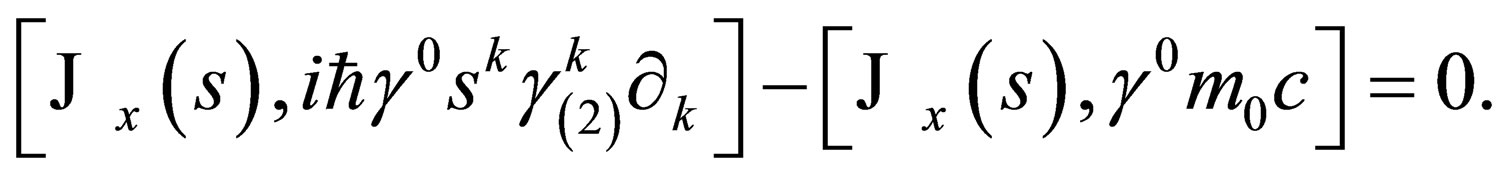 (A.4)
(A.4)
In this way, our task is now much easier, if we can show that
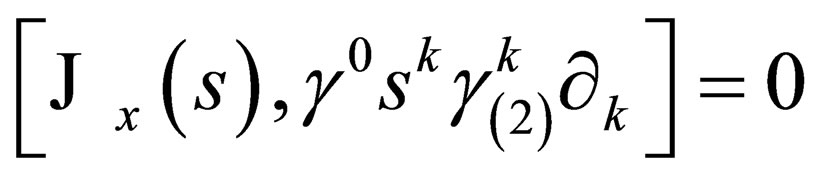 and
and we accomplish our mission. Let us start with the easier of the two, that is, show that
we accomplish our mission. Let us start with the easier of the two, that is, show that . Clearly:
. Clearly:
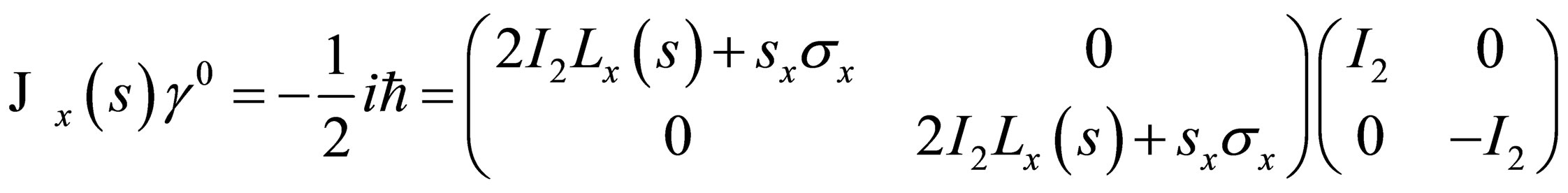 , (A.5)
, (A.5)
so that:
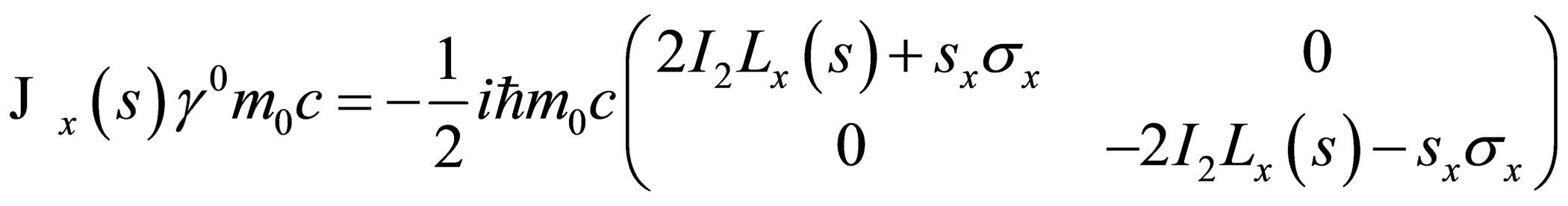 , (A.6)
, (A.6)
and:
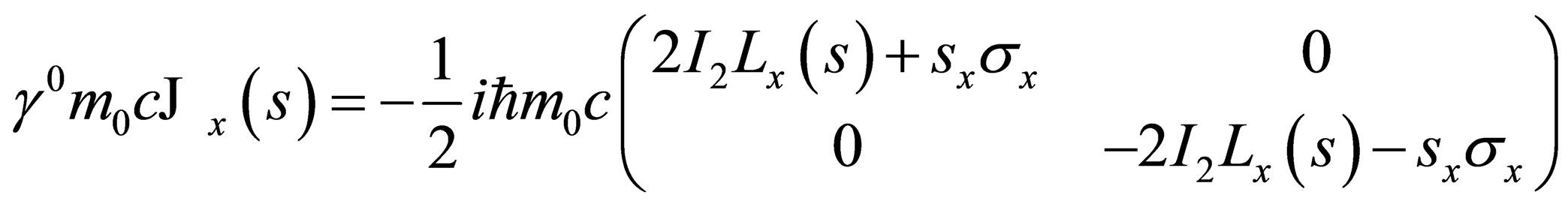 . (A.7)
. (A.7)
Now, subtracting (A.7) from (A.6), one obtains the desired result, namely . We are now left with demonstrating that
. We are now left with demonstrating that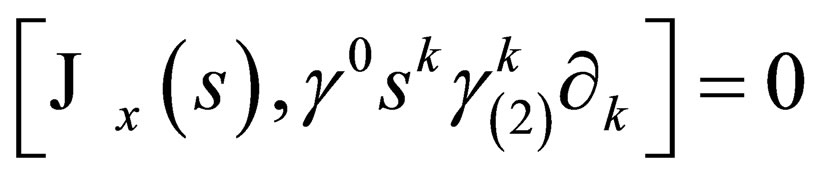 .
.
Clearly, upon correct algebraic operations, one can verify that:
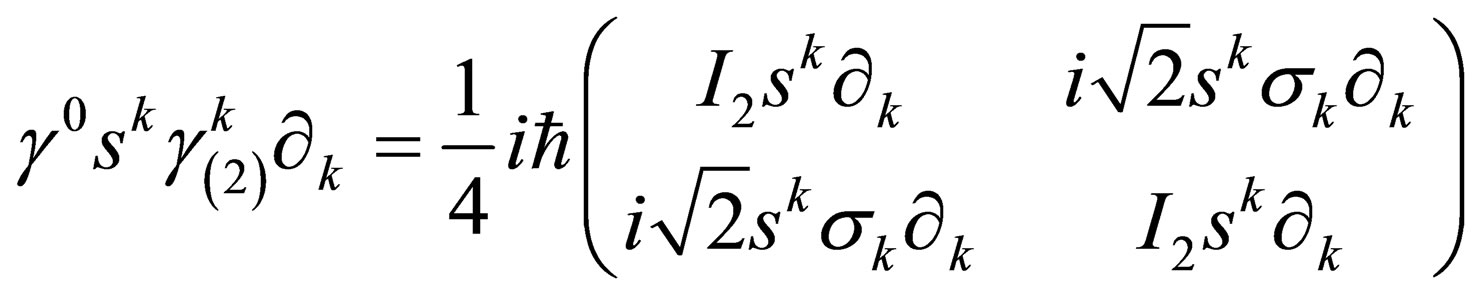 (A.8)
(A.8)
so that  is such that:
is such that:
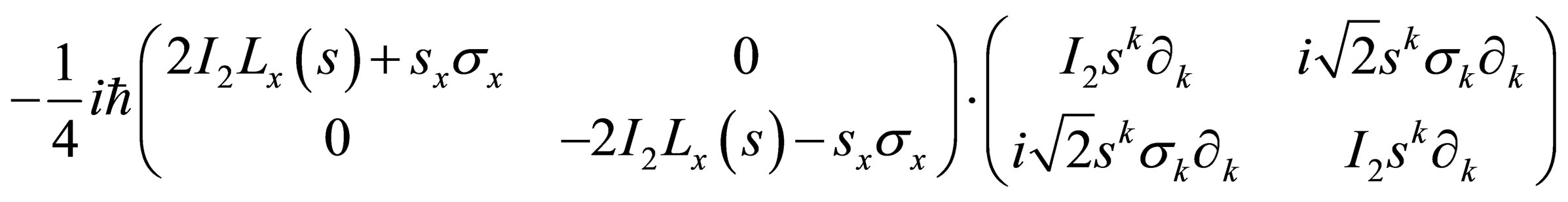 , (A.9)
, (A.9)
which is equal to:
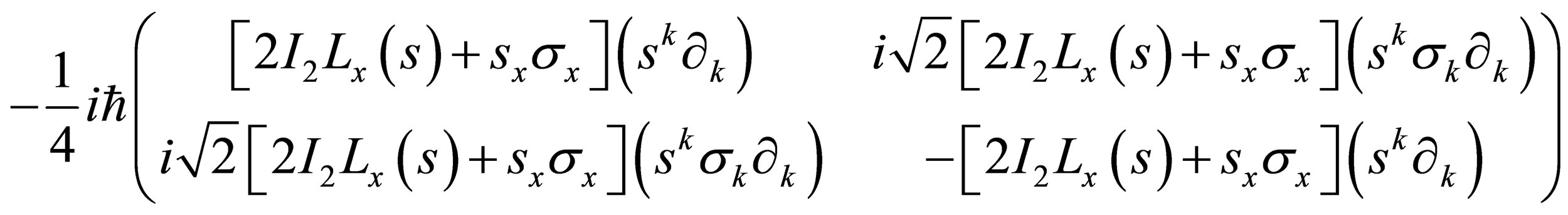 , (A.10)
, (A.10)
so that 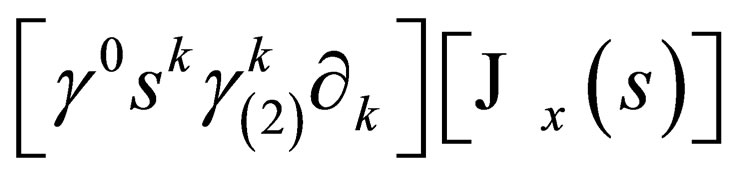 is such that:
is such that:
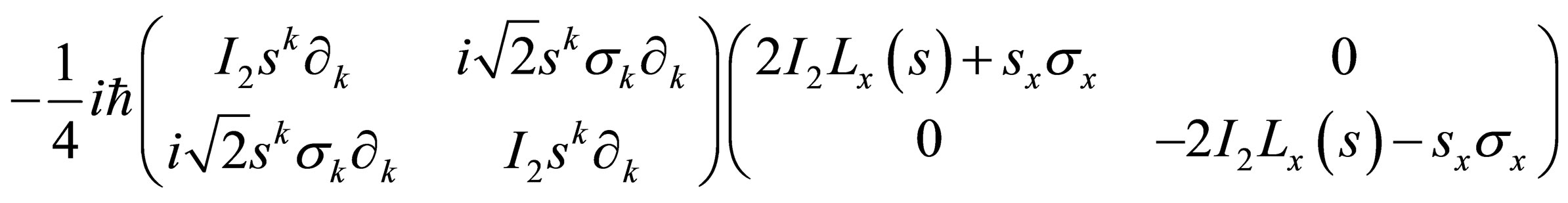 , (A.11)
, (A.11)
which invariably implies that:
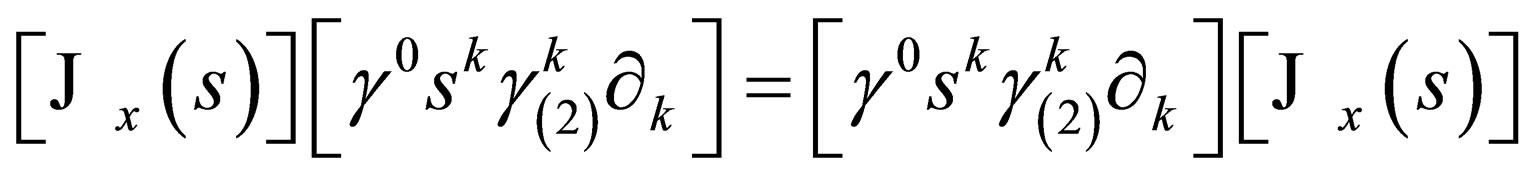 hence we arrive at our desired result, namely,
hence we arrive at our desired result, namely,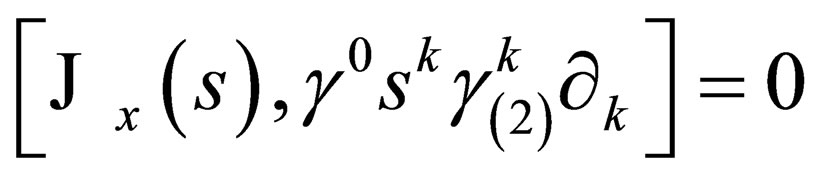 . Hence, according to our earlier arguments, it follows that the main result
. Hence, according to our earlier arguments, it follows that the main result
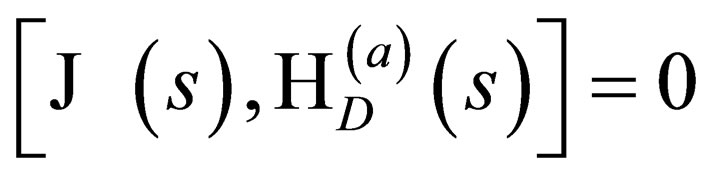 for-all
for-all 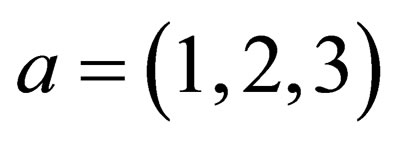 and for-all
and for-all
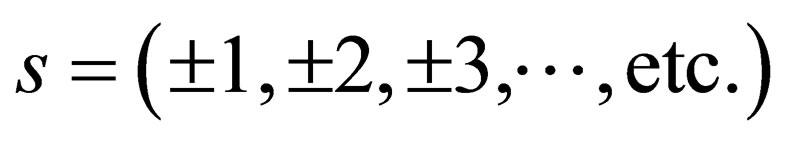 is thus attained.
is thus attained.
NOTES
1NB: This modified Einstein energy-momentum relation (1.1) leads to a Lorentz invariant modified Dirac equation.
2In Equation (1.8) above, the term 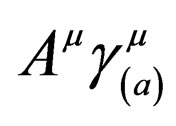 must be treated as a single object with one index
must be treated as a single object with one index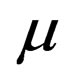 . This is what this object is. One can set
. This is what this object is. One can set . The problem with this setting is that we need to have to object
. The problem with this setting is that we need to have to object 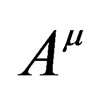 and
and  clearly visible in the equation.
clearly visible in the equation.
3There is a difference between Lorentz invariance and Lorentz covariance. In most cases as in the present, Lorentz invariance is used to mean Lorentz covariance. We are not going to go onto explaining what is the difference between the two. We sincerely believe that our target readership knows this and if they do not, they have access to consult any good textbook that deals with the theory of relativity (special/general). The usual Dirac equation is Lorentz covariant and not Lorentz invariant—this needs to be stated categorically clear. We have chosen to use the term Lorentz invariance instead of Lorentz covariance because the term Lorentz invariance is what is usually used. In-order that we are on the same level of understanding with the general reader, we do not have to deviate from the standard terminology.

