Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28568,10 pages DOI:10.4236/jmp.2013.43042
Numerical Study of the Threshold Intensity Dependence on Wavelength in Laser Spark Ignition of Molecular Hydrogen Combustion
1Department of Physics, Girl’s Faculty of Science, King Abdul-Aziz University, Jeddah, KSA
2Physics Department, Faculty of Science, Cairo University, Giza, Egypt
3National Institute of Laser Enhanced Science-Cairo University, El-Giza, Egypt
Email: galila@sci.cu.edu.eg, gamaly@yahoo.com
Received December 29, 2012; revised January 30, 2013; accepted February 10, 2013
Keywords: Laser Wavelength; Hydrogen Gas; Threshold Intensity; Electron Energy Distribution Function; Combustion; Spark Ignition
ABSTRACT
A numerical investigation of laser wavelength dependence on the threshold intensity of spark ignition in molecular hydrogen over a wide pressure range is presented. A modified electron cascade model (Gamal et al., 1993) is applied under the experimental conditions that carried out by Phuoc (2000) to determine the threshold intensity dependence on gas pressure for spark ignition in hydrogen combustion using two laser wavelengths namely; 1064 nm and 532 nm. The model involves the solution of the time dependent Boltzmann equation for the electron energy distribution function (EEDF) and a set of rate equations that describe the change of the formed excited molecules population. The model takes into account most of the physical processes that expected to occur in the interaction region. The results showed good agreement between the calculated thresholds for spark ignition and those measured ones for both wavelengths, where the threshold intensities corresponding to the short wavelength (532 nm) are found to be higher than those calculated for the longer one (1064 nm). This result indicates the depletion of the high density of low energy electrons generated through multi-photon ionization at the short wavelength via electron diffusion and vibrational excitation. The study of the EEDF and its parameters (viz, the temporal evolution of: the electron density, ionization rate electron mean energy…) revealed the important role played by each physical process to the spark ignition as a function of both laser wavelength and gas pressure. More over the study of the time variation of the EEDF explains the characteristics of the ignited spark at the two wavelengths for the tested pressure values.
1. Introduction
Several fundamental analytical methods as well as experimental studies have been initiated to elucidate the interactions associated with the phenomenon of laser spark ignition in a suitable gas. The generated high electron density could continue to absorb energy from the focused laser beam developing eventually what is called laser sustain plasma.
It is of critical importance to determine the laser conditions at which a spark is produced. A knowledge of these conditions is practically important not only for fundamentally understanding the ignition process, but also for the selection of lasers optics windows and beam delivery system for the design of practical laser to be used in the measurement for studying the laser spark ignition.
Although a considerable bodies of study on laser induced breakdown in gases have been reported (see for example [1-8]), the breakdown phenomenon of common combustion gases such as hydrogen has not been available. Because of the importance of such phenomenon, in various applications it attracted the attention of many researchers, in particular the mechanism that convert the laser energy to thrust energy or mechanical energy that could be approached via high power laser produced plasma (LPP) in a gas breakdown process [9-13].
Due to the high efficiency of the molecular hydrogen gas to convert the laser energy into thermal energy, researchers were interested to study this phenomenon in this gas owing to its importance as a thrust gas in rockets or space vehicles. Initially this phenomenon was studied using a CO2 laser radiation [14,15], later on studies are followed to measure the laser threshold intensity for plasma formation in this gas using lasers that operating with wavelengths in the UV, visible and IR regions over a wide range of the gas pressure. Among these studiesthat carried out by [6,16] during their study of antiStokes Raman scattering using two different focal length lenses to focus a 248 nm KrF laser beam into molecular hydrogen gas at a wide pressure range. They observed an optical breakdown at the beam waist of the focused pump beam which is found to be a major limiting factor when one attempts to increase the pump intensity. These measurements are investigated by [17]. In an another attempt in [5], Phuoc (2000) measured the threshold intensity of molecular hydrogen laser spark ignition using the fundamental and second harmonic of a Nd:Yag laser source at wavelengths 1064 nm and 532 nm respectively with pulse length 5.5 ns, over a gas pressure range extended from 150 torr to 3000 torr. This measurement showed that the threshold intensities corresponding to the shorter wavelength lie above those obtained for the longer one over the gas pressure range tested experimentally. This was attributed to the effect of the high rate of diffusion losses at the shorter laser wavelength. To find out the origin of this high threshold intensities corresponding to the shorter laser wavelength (532 nm), in this work we represents a numerical investigation of the measurements given in this experiment [5]. In doing so, a modified numerical electron cascade model [17,18] previously developed by [19] is applied to clarify the physical processes responsible for the laser spark ignition in molecular hydrogen as a function of both laser wavelength gas pressure. This model based on the solution of the time dependant Boltzmann equation for the Electron Energy Distribution Function (EEDF) together with a set of rate equations describing the rate of change of the excited states population formed through the interaction. The modified model takes into account the possible physical processes that might take place during the interaction to suit the molecular structure of the hydrogen gas among them rotational and vibrational excitation, diffusion losses, attachment, dissociation and recombination. In this model the effect of vibrational excitation is treated over two electron energy regimes; at the low electrons energy range (<3.0 eV) this process is taken as a loss term in the equation that represent the rate of electron energy gain from the laser field. For the higher energy electrons (>3.0 eV) however, the effect of this process is introduced in this equation as loss process in the inelastic collision terms. For realistic computational results this model takes into account the exact correlation between the electron energy and cross-sections or rate coefficients of each of the physical processes encountered in this analysis. The results of computations determined the threshold intensities as a function of the gas pressure the physical processes responsible for spark ignition and plasma formation are assigned through the study of the electron energy distribution function and its parameters.
2. Theoretical Formulation
2.1. Basic Equation
A detailed description of the model is given in [18,19]. Here we summarize only the outlines of the model where the electrons gain energy from the laser field through inverse Bremsstrahlung absorption, while their initial generation proceeds via multi-photon ionization process and grows during collisional ionization of ground state as well as photo-ionization and collisional ionization of the formed excited states.
In our computations the hydrogen molecule is treated as four level molecule which consists of: a ground state, two electronics excited states; the : state at 8.85 eV, and the
: state at 8.85 eV, and the 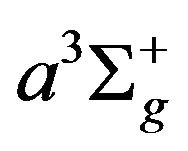 state at 12.0 eV, and the ionized state. The vibrational and rotational structures of the molecule are considered only for the ground
state at 12.0 eV, and the ionized state. The vibrational and rotational structures of the molecule are considered only for the ground  state.
state.
Therefore the model encounters the collisional and radiative processes given as: 1) electron inverse Bremsstrahlung absorption, 2) electron impact excitation of the 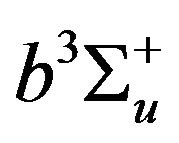 state, by electrons of energy ε > 8.85 eV, 3) electron impact excitation of the
state, by electrons of energy ε > 8.85 eV, 3) electron impact excitation of the 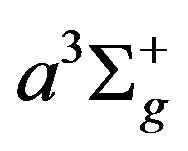 state, by electrons of energy ε > 12.0 eV, 4) electron impact excitation of the vibrationally excited states
state, by electrons of energy ε > 12.0 eV, 4) electron impact excitation of the vibrationally excited states  over the energy range 1.0 - 10.0 eV, 5) electron impact ionization of ground state molecule with electrons having energies ε > 15.43 eV, 6) collisional ionization from the lower excited state by electrons having energies ε > 15.43 - 8.85 eV, 7) collisional ionization from the higher excited state by electrons having energies ε > 15.43 - 12.0 eV, 8) photo-ionization of the lower excited
over the energy range 1.0 - 10.0 eV, 5) electron impact ionization of ground state molecule with electrons having energies ε > 15.43 eV, 6) collisional ionization from the lower excited state by electrons having energies ε > 15.43 - 8.85 eV, 7) collisional ionization from the higher excited state by electrons having energies ε > 15.43 - 12.0 eV, 8) photo-ionization of the lower excited  state, 9) photo-ionization of the higher excited
state, 9) photo-ionization of the higher excited 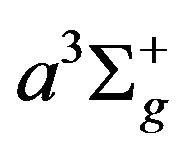 state, 10) rotational excitation of the ground state molecule, (this process is treated as an elastic loss mechanism), 11) dissociation of the excited molecules in the
state, 10) rotational excitation of the ground state molecule, (this process is treated as an elastic loss mechanism), 11) dissociation of the excited molecules in the 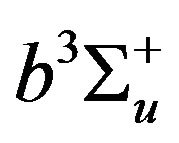 state, into two neutral fragments in the electronic ground state, 12) recombination losses and, 13) diffusion of electrons out of the focal volume.
state, into two neutral fragments in the electronic ground state, 12) recombination losses and, 13) diffusion of electrons out of the focal volume.
On the basis of these physical processes, the time evolution of the electron energy distribution function 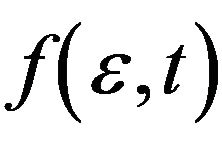 described by Boltzmann equation is written as
described by Boltzmann equation is written as
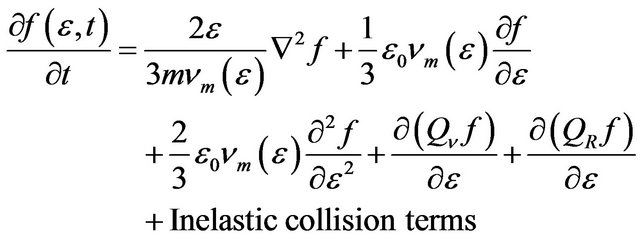 (1)
(1)
where 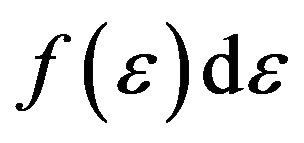 represents the number density of electrons with energies in the range between
represents the number density of electrons with energies in the range between 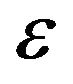 and
and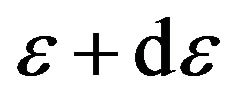 ,
,  is the average oscillatory energy of an electron in the laser field with an electric field amplitude E and angular frequency w,
is the average oscillatory energy of an electron in the laser field with an electric field amplitude E and angular frequency w,  is the momentum transfer collision frequency between an electron and a molecule, and Qv and QR represent the rates of transfer of energy from an electron of energy
is the momentum transfer collision frequency between an electron and a molecule, and Qv and QR represent the rates of transfer of energy from an electron of energy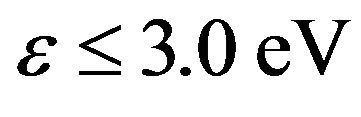 , to vibrational and rotational levels respectively.
, to vibrational and rotational levels respectively.
In this equation, the first term on the right-hand side represents the rate of electrons loss from the radiated volume due to diffusion. Here, we shall follow the custom to rewriting this by setting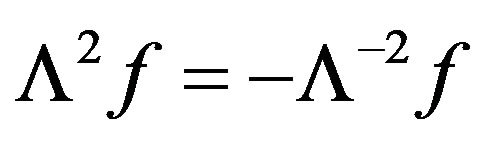 , where Λ is the characteristic diffusion length. This length characterizes the distance over which a particle should diffuse in order to be lost from the plasma. Following standard optical focal theory, the minimum focal volume is assumed to be cylindrical [20] of radius
, where Λ is the characteristic diffusion length. This length characterizes the distance over which a particle should diffuse in order to be lost from the plasma. Following standard optical focal theory, the minimum focal volume is assumed to be cylindrical [20] of radius 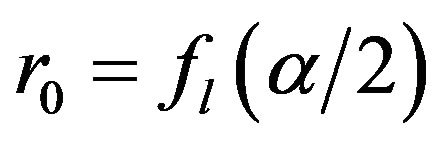 and axial length
and axial length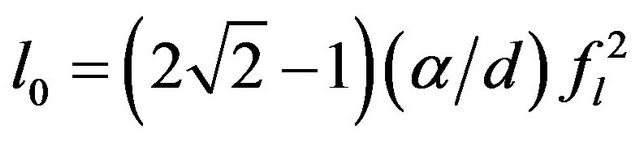 , where fl is the focal length of the lens, d is the diameter of the unfocused laser beam and α the corresponding beam divergence [21]. The second term expresses the electron energy gain; the third term is referred to diffusion of electrons along the energy axis, while the last two terms describe the elastic collision energy loss by electrons through vibrational and rotational excitation respectively. The inelastic collisional terms include generation of electrons with energy
, where fl is the focal length of the lens, d is the diameter of the unfocused laser beam and α the corresponding beam divergence [21]. The second term expresses the electron energy gain; the third term is referred to diffusion of electrons along the energy axis, while the last two terms describe the elastic collision energy loss by electrons through vibrational and rotational excitation respectively. The inelastic collisional terms include generation of electrons with energy 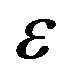 through ionization of ground and excited molecules as well as molecular excitation by electron impact. It also comprises the loss terms due to vibration excitation, molecular dissociation besides the electron loss processes through electron recombination. Under the experimental conditions considered in this analysis [5], superelastic collisions from the electronically and vibrationally excited states, as well as radiative recombination of the hydrogen molecule are neglected. Dissociative attachment from the vibrationally excited molecules
through ionization of ground and excited molecules as well as molecular excitation by electron impact. It also comprises the loss terms due to vibration excitation, molecular dissociation besides the electron loss processes through electron recombination. Under the experimental conditions considered in this analysis [5], superelastic collisions from the electronically and vibrationally excited states, as well as radiative recombination of the hydrogen molecule are neglected. Dissociative attachment from the vibrationally excited molecules 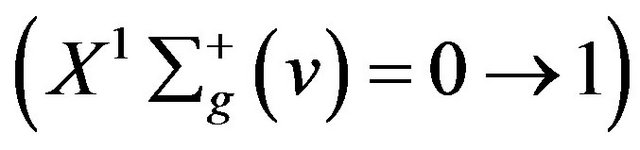 is also ignored. This process mainly depends on the high energy range of the vibrational states [15], which are not considered in our calculation.
is also ignored. This process mainly depends on the high energy range of the vibrational states [15], which are not considered in our calculation.
2.2. Cross Sections and Rate Coefficients
Empirical formulae for collisional cross sections are obtained using curve-fitting technique for the most recent experimental data published in literature by [22].
2.2.1. Cross Section for Momentum Transfer
The momentum transfer cross section was obtained as a function of the electron energy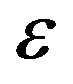 , using a least-squares fit for experimentally measured values given by [23] and is represented by
, using a least-squares fit for experimentally measured values given by [23] and is represented by
 (2)
(2)
2.2.2. Vibrational Cross Sections
In general, vibrational losses in hydrogen represent an important energy sink for electrons which cover a wide range of electron energies (1 eV < ε < 11 eV). Here, these losses are considered as being due to elastic collisions for electron energies ε < 3 eV, and as being due to inelastic collisions for electron energies in the range 3 eV < ε < 11 eV. Corresponding expressions for cross sections based on curve-fitting of experimental data given by [24,25] for the low and high energy ranges respectively are:
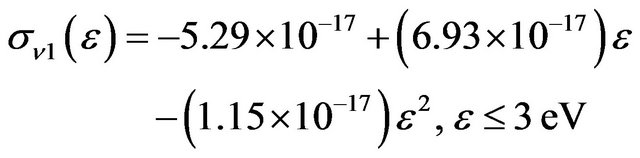 (3)
(3)
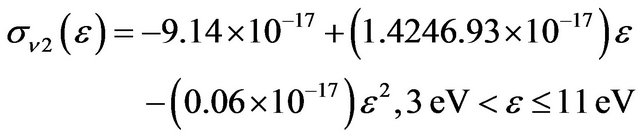 (4)
(4)
2.2.3. Cross Sections for Electronic Excitation
The obtained formulae for cross sections of the two excited electronic states considered here are represented by [22]
 (5)
(5)
 (6)
(6)
2.2.4. Ionization Cross Section of Ground State Molecules
The expression for the ionization cross section was derived from experimental measurements carried out by [26], and is given by:
 (7)
(7)
2.2.5. Stepwise Collisional Ionization Rate Coefficients
Owing to lack of experimental data, rate coefficients for collisional ionization of the two electronic excited states are obtained using an analytical formula given by [27] as:
 (8)
(8)
where k = 1, 2 indicate the two excited states and Ɛki is the energy difference between each of the excited states and the ionization limit, 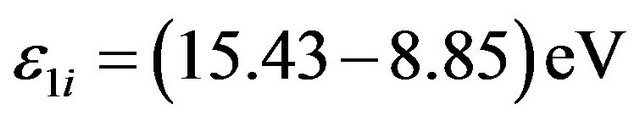 and
and  respectively.
respectively.
2.2.6. Photo-Ionization Coefficients of the Excited States
The photo-ionization coefficients of the excited states are estimated using a formula given by [28] as:
 (9)
(9)
where s is the photo-absorption cross section of a molecule, u is the frequency of the laser light and K is the number of photons absorbed by an excited molecule leading to its ionization . Table 1 shows the calculated values of the multi-photon absorption coefficient for the two wavelengths together with the excitation energies, the number of absorbed photons and the residual energy carried out by the free electron.
. Table 1 shows the calculated values of the multi-photon absorption coefficient for the two wavelengths together with the excitation energies, the number of absorbed photons and the residual energy carried out by the free electron.
2.2.7. Rotational Excitation Cross Section
As a function of the electron energy, the cross section for rotational excitations of the ground state molecule can be represented by the following expression, which is based on the experimental results of [23,25]:
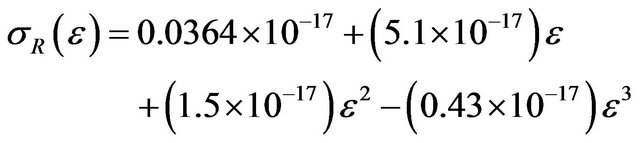 (10)
(10)
2.2.8. Dissociation Cross Section of the Electronically Excited Molecules
The expression of the dissociation cross section is obtained from the experimental data of [29] as:
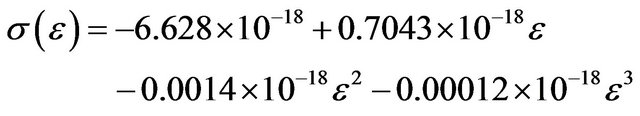 (11)
(11)
2.2.9. Recombination Rate Constant
The three body recombination rate constant as a function of the electron energy is taking from a relation given by [30] as:
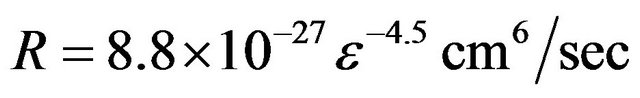 (12)
(12)
2.2.10. Electron Diffusion Rate
In this work the rate of diffusion losses is defined as:
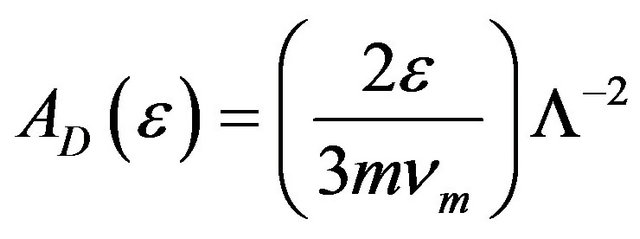 (13)
(13)
Here, the characteristic diffusion length Λ is considered to be energy independent. Adopting the experimenttal conditions considered in this analysis [5], where the beam mode of the laser pulse is taken to be close to Gaussian, so that the near focus may approximately be expressed in a cylindrical shape of radius r0 and length l0. Thus the characteristic diffusion length is written as,
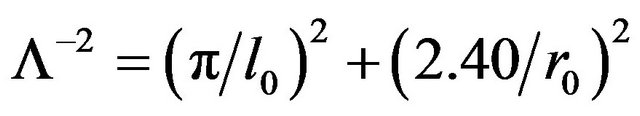 (14)
(14)
2.3. Method of Calculation
Equation (1) is solved numerically using a step-by-step integration method. The energy step-length Dɛ is chosen so that the complete energy distribution could be represented by about 25 equally spaced steps. This covers and exceeds the first ionization energy threshold of the molecular hydrogen (15.43 eV). The derivatives 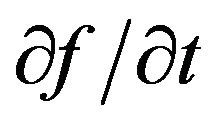 and
and 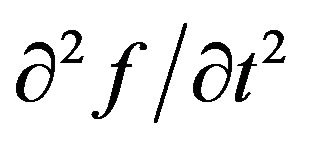 are evaluated using the finite difference technique. The inelastic collision terms (ionization and excitation as well as loss processes) could have been included as difference terms in Equation (1), but there are good reasons for treating them separately [19]. The temporal variation of the laser intensity in the focal volume is assumed to have a Gaussian distribution. The focal volume is determined using the geometric optics and is assumed to have a cylindrical shape. In these calculations the breakdown criteria is taken as the attainment of degree of fractional ionization d » 0.1% of the neutral gas molecules present in the focal volume.
are evaluated using the finite difference technique. The inelastic collision terms (ionization and excitation as well as loss processes) could have been included as difference terms in Equation (1), but there are good reasons for treating them separately [19]. The temporal variation of the laser intensity in the focal volume is assumed to have a Gaussian distribution. The focal volume is determined using the geometric optics and is assumed to have a cylindrical shape. In these calculations the breakdown criteria is taken as the attainment of degree of fractional ionization d » 0.1% of the neutral gas molecules present in the focal volume.
4. Results and Discussion
The modified electron cascade model is applied to investigate the experimental measurements that carried out by [5]. This was done by calculating the threshold intensity required to produce spark ignition in molecular hydrogen combustion corresponding to the experimental conditions of Phuoc where a Nd:YAG laser source operating at its fundamental and second harmonic with wavelengths 1064 nm and 532 nm respectively of pulse duration 5.5 ns is used to produce plasma in molecular hydrogen over a wide range of the gas pressure. Figure 1 show the calculated threshold irradiance for plasma generation as a function of gas pressure at wavelengths 1064 nm (solid curve) and 532 nm (dashed curve). For an easy compari
Table 1. The calculated values of the multi-photon ionization coefficient.

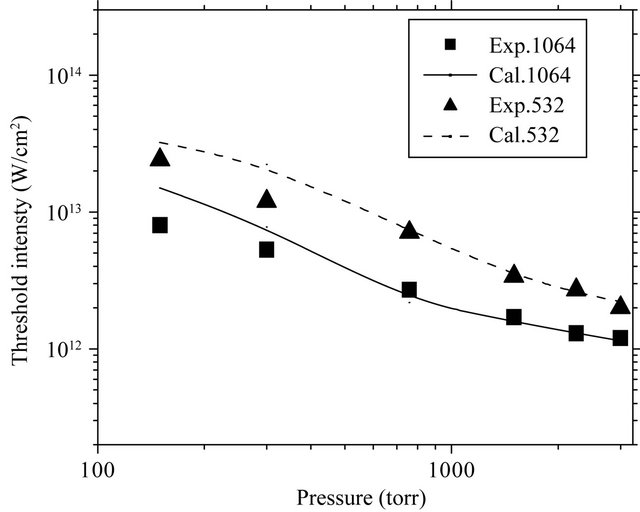
Figure 1. Comparison between the calculated threshold intensities and the measured ones as a function of gas pressure at wavelengths 1064 mm (solid curve) and 532 mm (dashed curve).
son the measured thresholds of [5] at the two laser wavelengths are also shown in this figure.
Reasonable agreement is obtained between the calculated and measured values for the two laser wavelengths with the thresholds obtained for the short wavelength 532 nm, lies above those obtained for the longer one 1064 nm. This result gives an evidence for the validity of the model to investigate the experimental measurements. This in turn encouraged us to carry out calculation of the EEDF to study the physical processes (responsible for spark ignition) dependence on the gas pressure for the two laser wavelengths. Figure 2 represents the EEDF calculated at the peak of the pulse 1) and at its end 2) for the two wavelengths 1064 nm (solid curves) and 532 nm (dashed curves), at three values of gas pressure namely; 150 torr (curve 1), 760 torr (curve 2) and 3000 torr (curve 3). These values are chosen deliberately since they are common in both laser wavelengths, and represent three different pressure regions.
From this figure it is noticed that the values of the calculated EEDF at the peak of the pulse are lower than those obtained at its end. Also a decrease of its values at 1.0 eV is observed only at higher pressures for the two considered wavelengths. This decrease reflects the effect of vibrational excitation with electrons having energies < 3.0 eV. Moreover the reduction of the EEDF at the low energy region indicates the high rate of inelastic collisional processes which acts to deplete electrons with high energies.
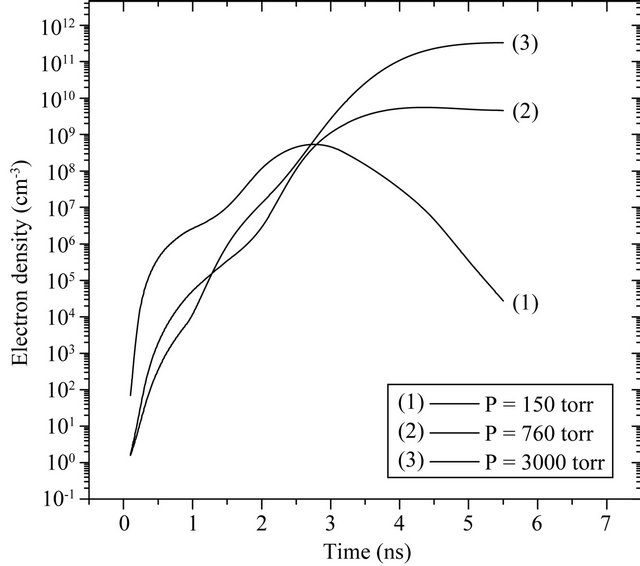
To study the physical process responsible for the source of the electron growth during the early stages of the laser pulse, Figure 3 represents the time evolution of the electron density obtained for the two laser wavelengths 1064 nm (a), 532 nm (b), at the gas pressures 150
 (a)
(a) (b)
(b)
Figure 2. The electron energy distribution function calculated at (a) the peak and (b) end of the laser pulse.
torr (curve 1), 760 torr (curve 2) and 3000 torr (curve 3).
It is shown from this figure that for the longer wavelength Figure 3(a) the growth of electrons start gradually up to the peak of the pulse for the whole the range, then after it increases much faster for the high pressure (curve 3). While for the low pressure its value decreases below the critical value of breakdown. This behavior indicates that for λ = 1064 nm the evolution of electrons proceeds
 (a)
(a) (b)
(b)
Figure 3. Time evolution of the electron density obtained for the two laser wavelengths. (a) λ = 1064 nm; (b) λ = 532 nm.
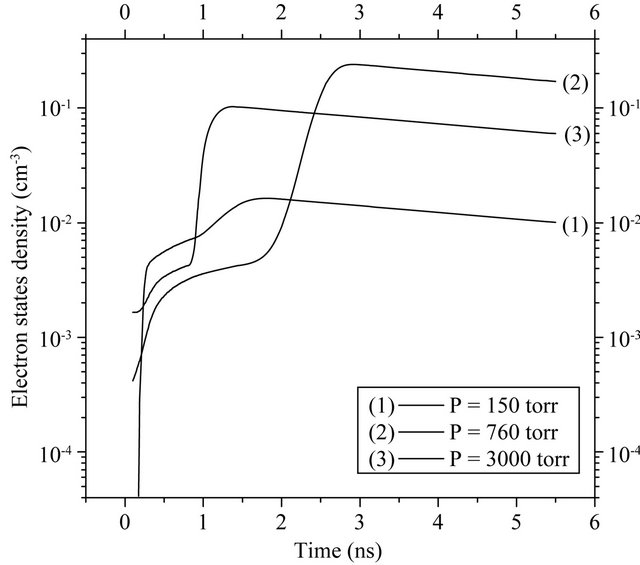
via collisional processes. Diffusion losses are effective only at the lower gas pressure region. At the shorter wavelength (λ = 532 nm), however, (Figure 3(b)) this later process is acting over the whole pressure range. This is shown from the low electron density observed during both the early stages as well as the descending part of the laser pulse. This high diffusion loss rate may be responsible for the depletion of the high electron density generated via multi-photon ionization of the formed excited molecules. This result is confirmed in Figure 4 which illustrates the time variation of the excited molecules population during the laser pulse at the three selected pressure values for the wavelengths (a) 1064 nm and (b) 532 nm.
 (a)
(a)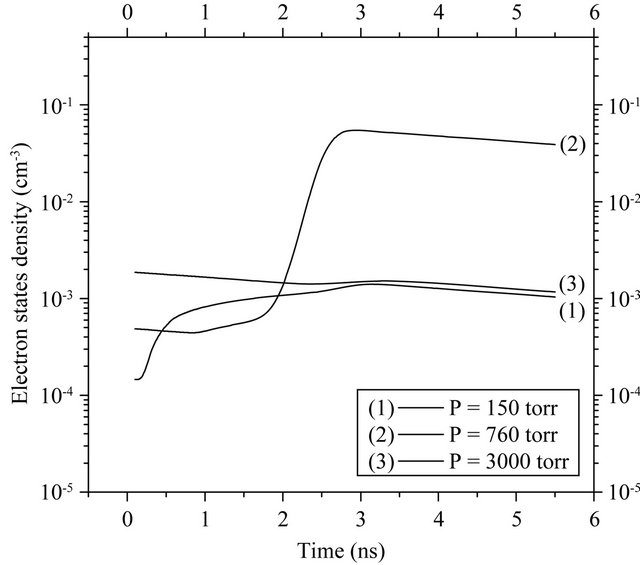 (b)
(b)
Figure 4. The time variation of the excited molecules population during the laser pulse. (a) λ = 1064 nm; (b) λ = 532 nm.
It is noticed here that the exhaustion of the excited molecules is more pronounced at the higher pressure value (curve 3) for the shorter wavelength (532 nm). At the longer wavelength (Figure 4(a)) however, the decrease of the excited molecular density is less effective even at the higher pressure as represented by curve (3). In addition at the atmospheric pressure the ionization of excited molecules are negligibly depleted so they do not contribute pronouncedly to the plasma generation as shown by curve (2) for the two wavelengths.
Figure 5 demonstrates the time variation of the electron mean energy calculated for the two laser wavelengths 1064 nm (a), 532 nm (b) at the three values of the gas pressure. This figure shows that the electron mean energy for both wavelengths almost show a flat top over the whole laser pulse. The high values observed at the low pressure for the 1064 nm (curve 1 in Figure 5(a)) indicates the low ionization rate at this pressure. Moreover the fast drop shown at the end of the pulse reflects the high rate of the diffusion loss process. It is also noticed her that the values of the electron mean energy increases as the gas pressure decrease. This confirms the less contribution of the inelastic collisions at low pressures.
In Figure 6 the time evolution of the ionization rate is represented for the same conditions. From this figure it is clear that at the low pressure value the ionization rate coincide for both wavelengths. It is noticed here that for
 (a)
(a)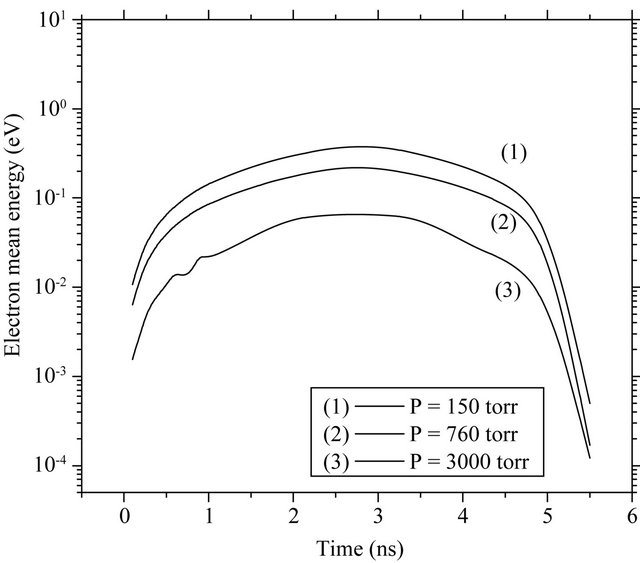 (b)
(b)
Figure 5. The electron mean energy calculated for the two laser wavelengths 1064 nm (a), 532 nm (b). (a) λ = 1064 nm; (b) λ = 532 nm.
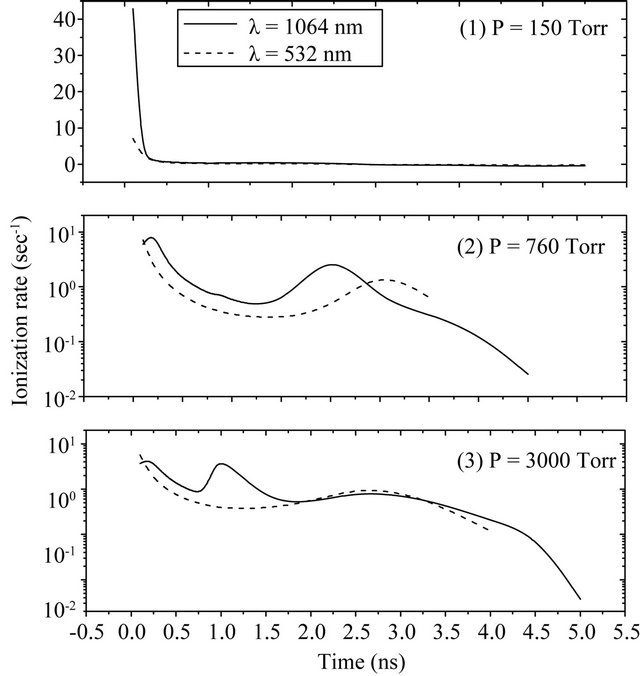
Figure 6. The time variation of the ionization rate calculated for laser wavelengths 1064 nm (a), 532 nm (b).
the shorter wavelength increasing the gas pressure results in a slight decreases of the ionization rate. This gives an evidence for the high competition of the diffusion and vibrational losses at this wavelength.
To assure this result, Figure 7 displays the calculated values of the time variation of the excitation rate at the considered gas pressure values for laser wavelengths 1064 nm (a), 532 nm (b). The study shown in this figure proved that at the low pressure region the excitation rate takes almost a constant value over the whole pulse duration. At the longer wavelength, this rate showed a noticeable peak coincides with that of the laser pulse at the atmospheric pressure. As the pressure increases this peak moves towards the early stages of the laser pulse. The appearance of such peak indicates the high rate of collisional processes at this wavelength. For the shorter wavelength (dashed curves) however, this rate remains almost at the same value for the high pressure range.
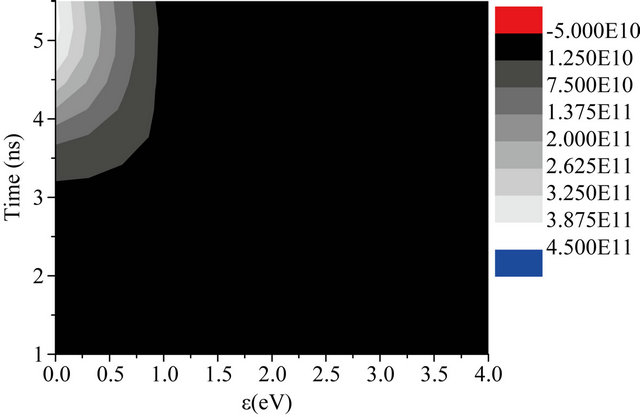
To find out the characteristics of the formed spark under the tested experimental conditions Figures 8-10 show the contour representation of the time evolution of the electron density corresponding to explicit electron energy range for the three values of gas pressures at the wavelengths (a) 1064 nm and (b) 532 nm. These figures examined precisely the time evolution and generation of the formed plasma as a function of both gas pressure and laser wavelength. It is clear from these figures that at low pressure (Figure 8) the plasma is mainly generated around the peak of the laser pulse. This behavior designates that at this pressure electrons are mainly produced through photoionization processes. As the gas pressure
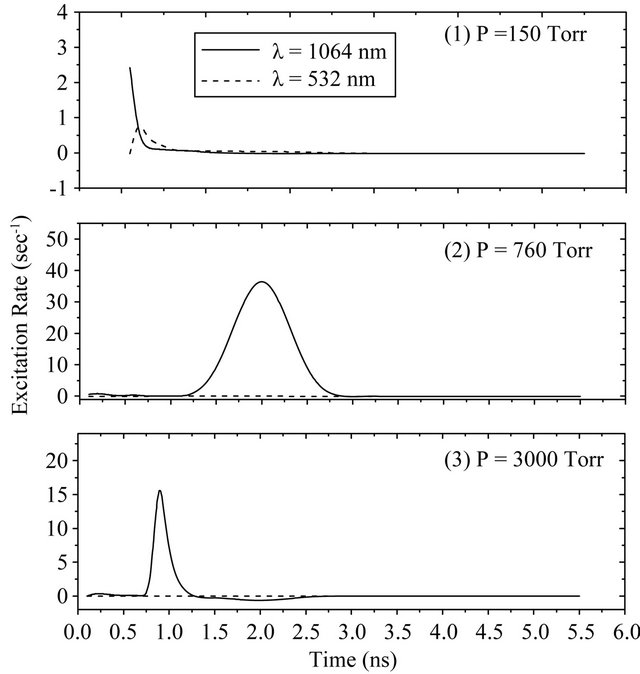
Figure 7. The excitation rate as function of time calculated at the considered gas pressure values for laser wavelengths 1064 nm (a), 532 nm (b).
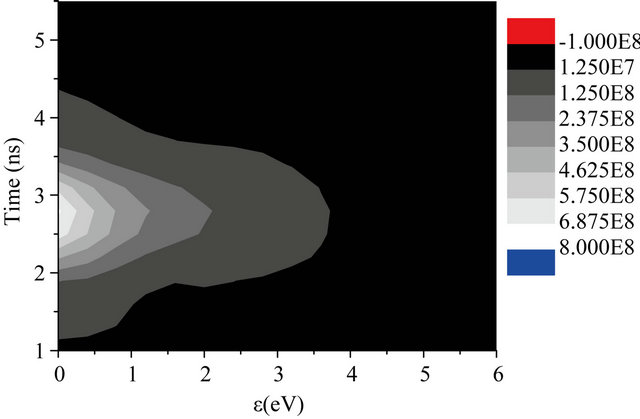 (a)
(a) (b)
(b)
Figure 8. Contour representation of the EEDF as function of time calculated at 150 torr for laser wavelengths 1064 nm (a), 532 nm (b). (a) λ = 1064 nm; (b) λ = 532 nm.
increases the plasma generation extends over a longer period during the descending part of the laser pulse. This indicates the important role played by collisional processes which are more effectives at high pressures. Moreover the size reduction of the formed plasma at the shorter wavelength shown in Figures 8, 9 and 10(b) gives an evidence for the high rate of energetic electron loss out of the focal volume through diffusion.
4. Conclusion
In the present work a modified electron cascade model is applied to investigate the experimental measurements that carried out by Phuoc (2000) [5] on hydrogen spark ignition using two laser wavelengths 1064 nm and 532 nm. In this experiment a Nd:YAG laser source operating at the two first harmonics with pulse duration 5.5 ns is used to produce spark ignition and combustion of molecular hydrogen over pressure range extended from 150 torr to 3000 torr. The calculations of the threshold intensity corresponding to the two laser wavelengths over the measured pressure range showed a reasonable agreement with the experimentally measured ones. This result confirmed the validity of the model, and in turn assured the
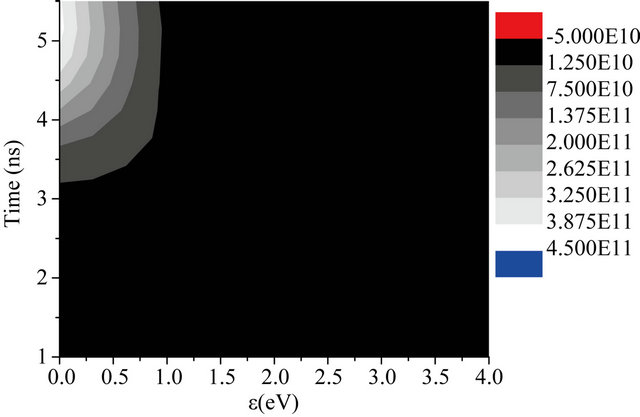 (a)
(a) (b)
(b)
Figure 10. The same as in Figure 8 but for pressure 3000 torr. (a) λ = 1064 nm; (b) λ = 532 nm.
assumed physical processes included into the model. Moreover the calculation of the EEDF as well as the time evolution of the electron density, electron mean energy and ionization and excitation rates, revealed the exact role played by low energy electrons through vibrational excitation and its competition with diffusion losses at the low pressure region for the wavelength 1064 nm and over the whole pressure range for the shorter wavelength 532 nm. The study of the time variation of the EEDF clarifies the exact period for spark ignition as well as its characteristics (size, electron density and temperature) as a function of both gas pressure and laser wavelength.
REFERENCES
- D. C. Smith and A. F. Haught, “Energy Loss Processes in Optical Frequency Gas Breakdown,” Physics Review Letters, Vol. 16, No. 24, 1966, pp. 1085-1088.
- D. E. Lencioni, “Laser Induced Air Breakdown for 1.06 mm Radiation,” Applied Physics Letters, Vol. 25, No. 1, 1974, pp. 15-17. doi:10.1063/1.1655259
- R. J. Dewhurst, J. Pert and G. J. S. A. Ramsden, “LaserInduced Breakdown in the Rare Gases Using Picosecond Nd:Glass Laser Pulses,” Journal of Physics B: Atomic and Molecular Physics, Vol. 7, No. 16, 1974, pp. 2281- 2290. doi:10.1088/0022-3700/7/16/025
- K. C. Byron and G. J. Pert, “Measurement of the Wavelength Dependence of the Threshold of Laser-Induced Gas Breakdown,” Journal of Physics D: Applied Physics, Vol. 12, No. 3, 1979, p. 409. doi:10.1088/0022-3727/12/3/010
- T. X. Phuoc, “Laser Spark Ignition: Experimental Determination of Laser-Induced Breakdown Thresholds of Combustion Gases,” Optics Communications, Vol. 175, No. 4-6, 2000, pp. 419-423. doi:10.1016/S0030-4018(00)00488-0
- T. Yagi and Y. Huo, “Laser-Induced Breakdown in H2 Gas at 248 nm,” Applied Optics, Vol. 35, No. 18, 1996, pp. 3183-3184. doi:10.1364/AO.35.003183
- S. Soubacq, P. Pignolet, E. Schall and J. Batina, “Investigation of a Gas Breakdown Process in a Lser-Plasma Experiment,” Journal of Physics D: Applied Physics, Vol. 37, No. 19, 2004, pp. 2686-2702. doi:10.1088/0022-3727/37/19/012
- J. J. Camacho, J. M. L. Poyato, L. Diaz and M. Santos, “Optical Emission Studies of Nitrogen Plasma Generated by IR CO2 Laser Pulses,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 40, No. 24, 2007, pp. 4573-4590. doi:10.1088/0953-4075/40/24/003
- N. H. Kemp, D. L. Rosen and H. H. Lenger, “Orbit-Raising and Maneuvering Propulsion: Research Status and Needs,” American Institute of Aeronautics and Astronautics, New York, 1984, pp. 73-94.
- D. Rosen, G. Weyl, N. Kemp and D. Ham, “Experimental and Theoretical Studies of Laser Propulsion Phenomenology,” Annual Technical Report, Physical Sciences Inc, Andover, 1984.
- A. Mertogul, D. Zerkle and H. Krier, “Investigation of CO2 Laser-Sustained Hydrogen Plasmas,” Journal of Propulsion and Power, Vol. 8, No. 5, 1992, pp. 1123-1125. doi:10.2514/3.23601
- G. Zeockler, M. Joseph, J. Green and P. Raitano, “A New Facility for Advanced Rocket Propulsion Research,” 29th AIAA, SAE, ASME and ASEE Joint Propulsion Conference and Exhibit, 28-30 June 1993, Monterey.
- T. Jordin Kare, “Laser Launch—The Second Wave,” AIP Conference proceedings of the First International Symposium on Beamed Energy Propulsion, Vol. 664, 2003, pp. 442-453.
- D. Keefer, R. Elkins, C. Peters and L. Jones, “Laser Thermal Propulsion,” Research Status and Needs, New York, 1983.
- C. Grose, M. Capitelli, M. Bacal, J. Bretagne and A. Lagana, “Progress in the Non-Equilibrium Vibrational Kinetics of Hydrogen in Magnetic Multicusp H− Ion Sources,” Chemical Physics, Vol. 117, No. 2, 1987, pp. 177-195. doi:10.1016/0301-0104(87)80120-9
- Y. Huo, K. Shimizu and T. Yagi, “Vacuum Ultraviolet Generation by Anti-Stokes Raman Scattering of KrF Laser Radiation in H2,” Journal of Applied Physics,Vol. 72, No. 8, 1992, pp. 3258-3263. doi:10.1063/1.351446
- Y. E. E.-D. Gamal, A. E. Khaled and M. A. Mahmoud, “Numerical Investigation of the Electron Dynamic Dependence on Gas Pressure in the Breakdown of Hydrogen by KrF Laser Radiation,” Optics & Laser Technology, Vol. 44, No. 7, 2012, pp. 2154-2160. doi:10.1016/j.optlastec.2012.03.009
- Y. E. E.-D. Gamal, M. S. Shafik and M. M. Khalil, “An Investigation of the Wavelength-Dependence of the Threshold Intensity of Laser Induced Breakdown of Molecular Hydrogen,” Journal of Physics D: Applied Physics, Vol. 26-40, 1993.
- C. Evans and Y. E. E.-D. Gamal, “Laser Induced Breakdown of Helium,” Journal of Physics D: Applied Physics, Vol. 13, 1980, pp. 1447-1458.
- A. D. MacDonald, “Microwave Breakdown in Gases,” Wiley, New York, 1966.
- N. Kroll and K. M. Watson, “Theoretical Study of Ionization of Air by Intense Laser Pulses,” Physical Review A, Vol. 5, No. 4, 1972, pp. 1883-1905. doi:10.1103/PhysRevA.5.1883
- G. Casanak, D. S. Cartwright, S. K. Sariavatava and S. Trajmar, “Electron Molecule Interactions and Their Applications,” Academic, New York, 1984,
- O. K. Gibson, “The Cross Sections for Rotational Excitation of H2 And D2 by Low Energy Electrons,” Australian Journal of Physics, Vol. 23, 1970, pp. 683-696.
- H. Earhart, L. Langhans, F. Linder and H. S. Taylor, “Resonance Scattering of Slow Electrons from H2 and CO Angular Distributions,” Physical Review, Vol. 173, No. 1, 1968, pp. 222-230. doi:10.1103/PhysRev.173.222
- F. Linder and H. Schmidt, “Experimental Study of Low Energy e-O2 Collision Processes,” Verlag der Zeitschrift für Naturforschung, Vol. 26, 1971, p. 1617.
- E. Rappd and P. Golden, “Total Cross Sections for Ionization and Attachment in Gases by Electron Impact. I. Positive Ionization,” Journal of Chemical Physics, Vol. 43, No. 5, 1965, pp. 1464-1479. doi:10.1063/1.1696957
- L. Vriens and A. Smeers, “Cross-Section and Rate Formulas for Electron-Impact Ionization, Excitation, Deexcitation, and Total Depopulation of Excited Atoms,” Physical Review, Vol. A22, No. 3, 1980, pp. 949-951. doi:10.1103/physreva.22.940
- C. G. Morgan “Laser-Induced Breakdown of Gases,” Reports on Progress in Physics, Vol. 38, No. 5, 1975, pp. 621-665. doi:10.1088/0034-4885/38/5/002
- M. J. Muumma and E. C. Zipf, “Dissociative Excitation of Vacuum Ultraviolet Emission Features by Electron Impact on Molecular Gases. I. H2 and O2,” Journal of Chemical Physics, Vol. 55, No. 4, 1971, pp. 1661-1669. doi:10.1063/1.1676294
- Yu. P. Raizer and Ya. B. Zel’dovich, “Physics of Shock Wave and High-Temperature Hydrodynamics Phenomena,” Academic Press, New York, 1966.


 (a)
(a) (b)
(b)