Journal of Modern Physics
Vol.3 No.2(2012), Article ID:17687,4 pages DOI:10.4236/jmp.2012.32020
A New Approach to the Ground State of Superfluid Fermi Gas near the Feshbach Resonance of d-Wave
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani62@yahoo.com
Received October 25, 2011; revised December 20, 2011; accepted January 8, 2012
Keywords: d-Wave Coupling; Superfluid; Gap Equation; Ground State
ABSTRACT
In this paper, the d-wave coupling near the Feshbach resonance is investigated. Furthermore, we investigate the analytic solution to the gap equation and the ground state at T = 0 through utilizing the Nozihres and Schmitt-Rink potential creating the two-body low-energy scattering amplitude, and minimizing energy. Necessarily, to obtain the ground state, the system energy must be minimized. With regards to the achieved energies, merely, μ0 or γ are variable; therefore, γ must be minimized to find the ground state. Moreover, considering the Fermi gas’s superfluidity at the temperature of T = 0, and by employing the potential model providing the two-body scattering amplitude, we investigate the analytic solution to the BCS problem for the d-wave coupling.
1. Introduction
We study and investigate the Fermi-gases pairing near the d-wave Feshbach resonance. Using Nozieres and SchmittRink potential that produces the two-body energy scattering amplitude, we have obtained an analytic solution of the gap equation and ground states by minimizing of energy at T = 0. Currently, there are considerable evidences for the formation of fermion pairs near Feshbach resonance [1,2]. The Feshbach resonance is a region where these fermion pairs strongly interact. Generally, the interaction in atomic gases is defined by a parameter called s-wave scattering length (a0). This quantity can be adjusted near the Feshbach resonance. The sign and size of a0 can be determined using an external magnetic field [3]. With regards to the scattering length a0, the atomic interactions in Feshbach resonance are divided into two domains. The domain a0 < 0 possesses the interaction of cooper pairs (BCS), and the domain a0 > 0 possesses the molecular interaction of fermion pairs (BEC or Bose-Einstein condensation) [4,5].
2. The Two-Body Scattering Amplitude According to the Scattering Matrix
The partial scattering amplitude of the  th wave (
th wave (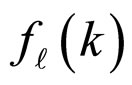 ) through scattering matrix
) through scattering matrix 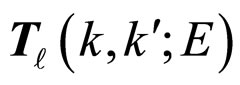 relates to the potential V(r) as the form below [6-13]:
relates to the potential V(r) as the form below [6-13]:
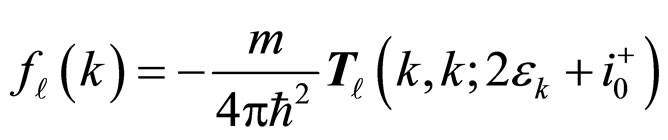 (1)
(1)
where 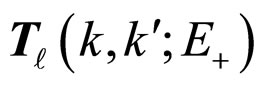 fulfills the following integral equation:
fulfills the following integral equation:
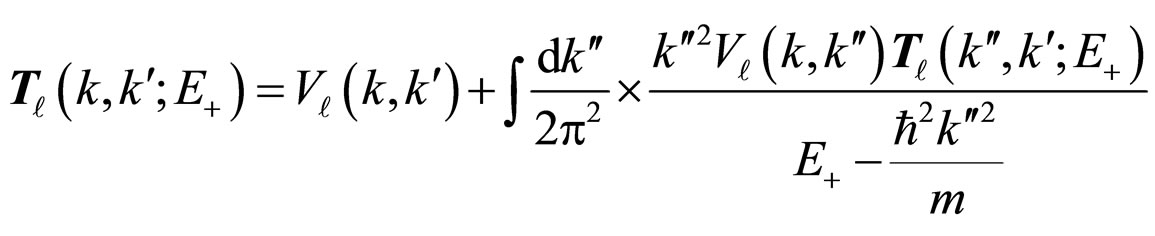 (2)
(2)
In order to obtain the scattering matrix, the expansion  is applied as follows [14]:
is applied as follows [14]:
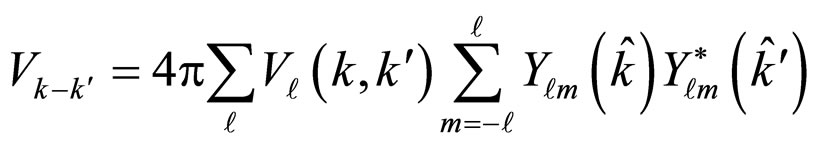 (3)
(3)
3. The Nozihres and Schmitt-Rink Potential
The Nozihres and Schmitt-Rink potential is used to avoid technical complexities [15]:
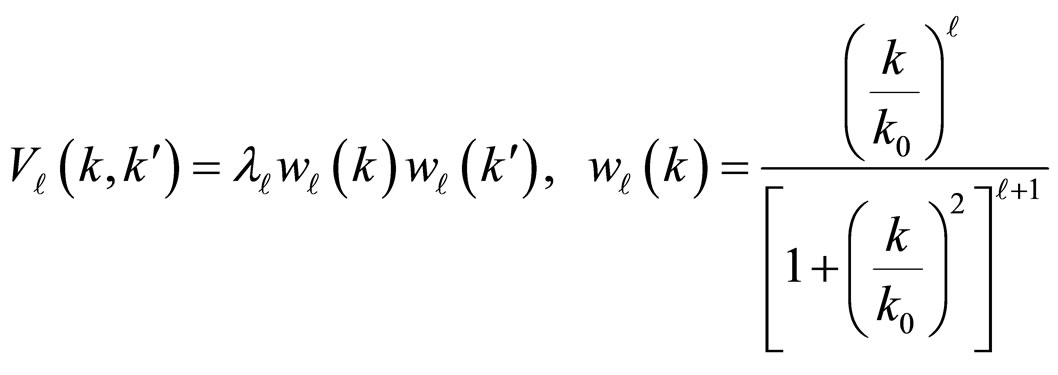 (4)
(4)
where 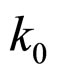 is the cut-off wave vector.
is the cut-off wave vector.
To achieve the scattering amplitude, the function  is defined as follows:
is defined as follows:
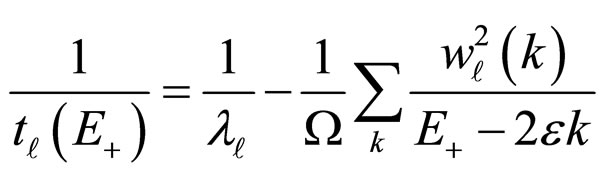 (5)
(5)
where 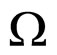 is the volume. Now, if we input the parameter below to Equation (5):
is the volume. Now, if we input the parameter below to Equation (5):
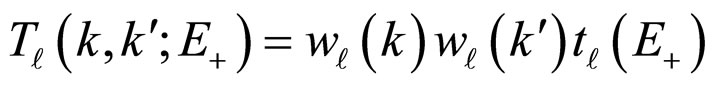 (6)
(6)
we achieve Equation (2). Also, Equation (5) is solved for . Through this method, we obtain
. Through this method, we obtain . By calculating the residues, the solution to Equation (5) is as the following form:
. By calculating the residues, the solution to Equation (5) is as the following form:
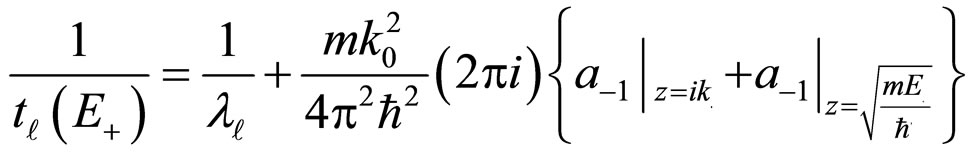 (7)
(7)
Finally, through employing Equations (1), (5), and (6), the amplitude of  equals:
equals:
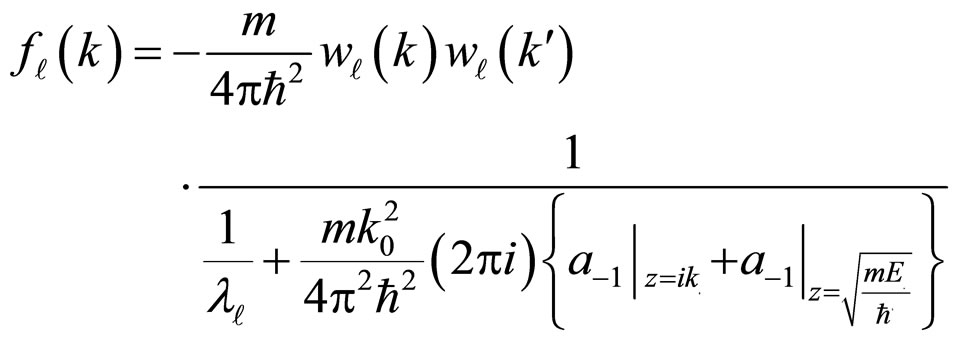 (8)
(8)
Therefore, the scattering amplitude for  at low energies is achieved as the form below:
at low energies is achieved as the form below:
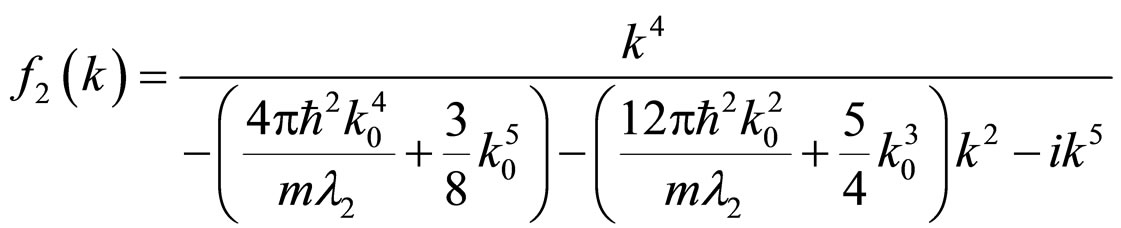 (9)
(9)
4. The Effective Range and Scattering Length for 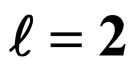
The partial two-body scattering amplitude of the 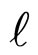 th wave at low energies is as follows [16]:
th wave at low energies is as follows [16]:
 (10)
(10)
where ,
, 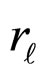 , and b are respectively the scattering amplitude, effective range, and potential range. The boundstate energy appears as a polar in the function
, and b are respectively the scattering amplitude, effective range, and potential range. The boundstate energy appears as a polar in the function 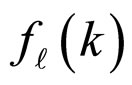 when k is the analytic continuation of pure imaginary axis [17- 19]. For
when k is the analytic continuation of pure imaginary axis [17- 19]. For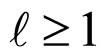 , the effective range in Equation (10) dominates the imaginary domain. Then, the bound-state energy equals [20-26]:
, the effective range in Equation (10) dominates the imaginary domain. Then, the bound-state energy equals [20-26]:
 (11)
(11)
Inputting 2 instead of 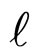 to Equation (10), and comparing it with Equation (9), we will have:
to Equation (10), and comparing it with Equation (9), we will have:
 (12)
(12)
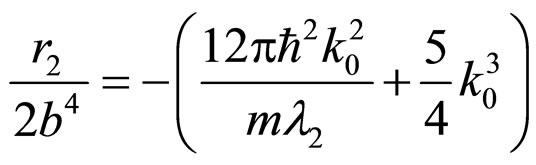 (13)
(13)
Removing  from the two above equations,
from the two above equations, 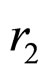 is achieved as the form below:
is achieved as the form below:
 (14)
(14)
On the other hand, in the Feshbach resonance,  inclines toward infinity [27], then:
inclines toward infinity [27], then:
 (15)
(15)
5. The System Energy and Energy Gap below the Transition Temperature
Through the BCS theory, the average energy and energy gap can be written as [28]:
 (16)
(16)
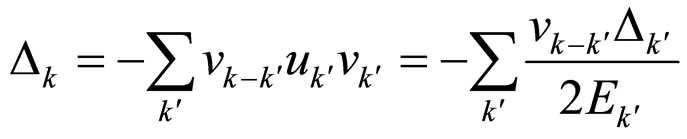 (17)
(17)
where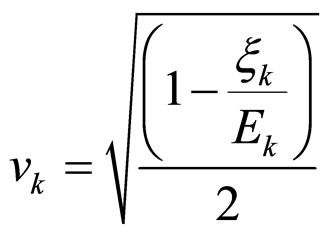 ,
,  ,
,  ,
, 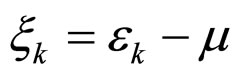 , Ω is the volume, and µ is the chemical potential. Applying the mentioned parameters, and inputting them to Equations (16) and (17), the system energy and energy gap are rewritten as follows:
, Ω is the volume, and µ is the chemical potential. Applying the mentioned parameters, and inputting them to Equations (16) and (17), the system energy and energy gap are rewritten as follows:
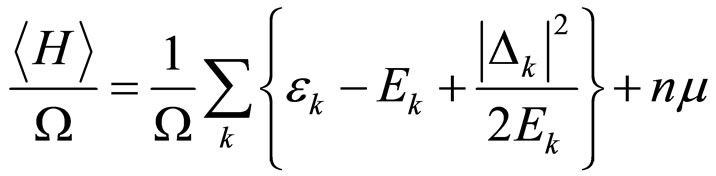 (18)
(18)
where n, the number of particles per volume unit, equals:
 (19)
(19)
 (20)
(20)
in which the multipliers of 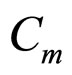 fulfills Equation (21):
fulfills Equation (21):
 (21)
(21)
Through utilizing Equations (20) and (21), we obtain:
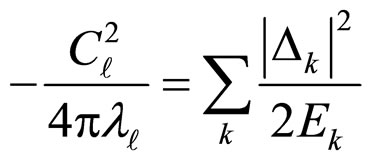 (22)
(22)
Under the transition temperature ( ),
), [29,30], and also considering that the gap is small, the system energy and n are written as follows:
[29,30], and also considering that the gap is small, the system energy and n are written as follows:
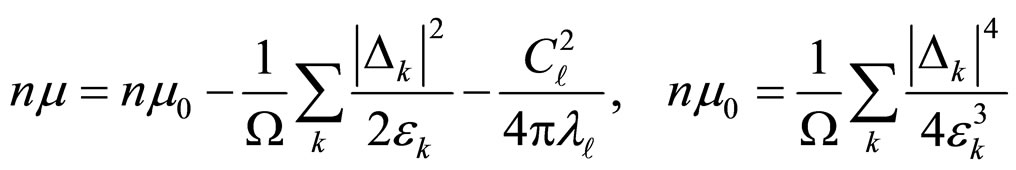 (23)
(23)
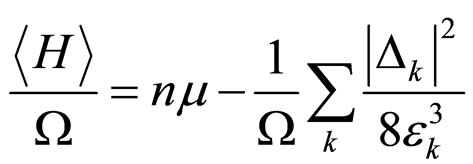 (24)
(24)
 (25)
(25)
On the other hand, the number of electrons under the Fermi level equals:
 (26)
(26)
Applying Equations (20) and (25), n for 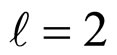 can be rewritten:
can be rewritten:
 (27)
(27)
Now, Equation (27) is input to Equation (15). Using Equation (26) and some calculations, we achieve:
 (28)
(28)
Utilizing Equations (11), (12), and (28):
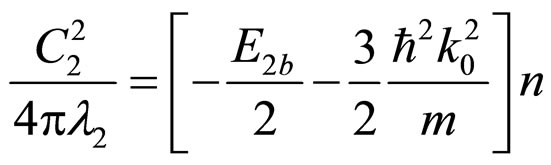 (29)
(29)
Through inserting Equation (29) into Equations (23) and (24):
 (30)
(30)
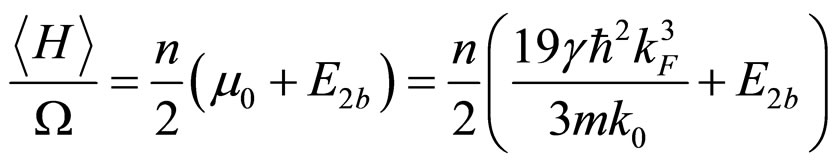 (31)
(31)
where , and the energy gap is transformed into the below form:
, and the energy gap is transformed into the below form:
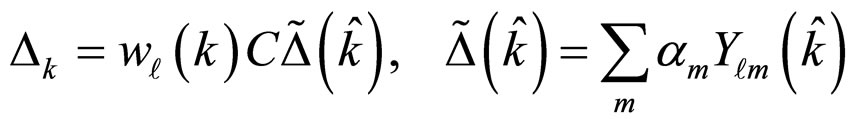 (32)
(32)
where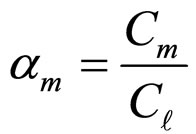 .
.
6. Results and Discussion
In this investigation and study, for the first time, we presented a novel work and obtained a new method and solution for calculating the ground state of superfluid Fermi gas near the Feshbach resonance of d-wave. The system energy must be minimized to obtain the ground state. If the achieved energies are considered, solely,  or
or 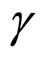 is variable; therefore,
is variable; therefore, 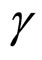 must be minimized to find the ground state. For this purpose, the Cartesian display of spherical harmonics is utilized, and
must be minimized to find the ground state. For this purpose, the Cartesian display of spherical harmonics is utilized, and  can be written as follows:
can be written as follows:
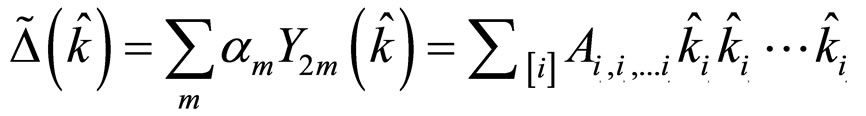 (33)
(33)
for :
:
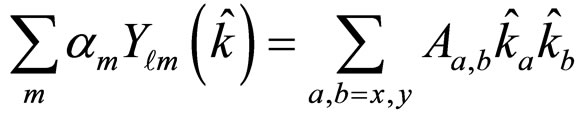 (34)
(34)
Through computing the energy gap expansion for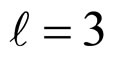 a general equation for
a general equation for 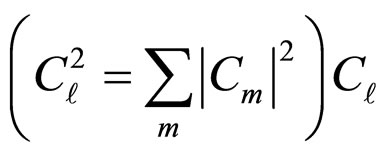 can also be obtained:
can also be obtained:
 (35)
(35)
which a more general equation for 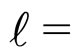 1, 2, and 3, can be written as follows:
1, 2, and 3, can be written as follows:
 (36)
(36)
However, we investigate single-particle excitations at T = 0 in the BCS-BEC crossover regime of a superfluid Fermi gas. We solve the Bogoliubov-de Gennes equations in a trap, including a tunable pairing interaction associated with a Feshbach resonance. We show that the single-particle energy gap Eg is dominated by the lowest-energy Andreev bound state localized at the surface of the gas.
7. Conclusions
In this paper, for the first time, we proposed a novel analytical approach toward the ground state of superfluid Fermi gas near the Feshbach resonance of d-wave. Also, the system energy and  for different
for different  s are achieved:
s are achieved:
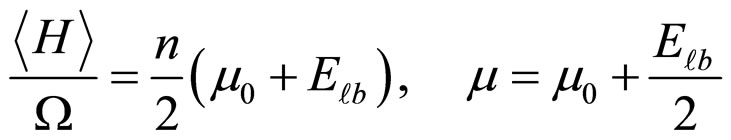 (37)
(37)
where 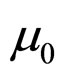 for various
for various  s are also different. The minimization of the system energy and ground state of superfluid Fermi gas for
s are also different. The minimization of the system energy and ground state of superfluid Fermi gas for 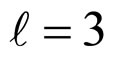 will be provided in another article.
will be provided in another article.
Since TrA = 0 and A is a symmetric matrix,
 . Therefore, the ground state has a random degeneracy; it means that the two below states are minimized.
. Therefore, the ground state has a random degeneracy; it means that the two below states are minimized.
 (38)
(38)
 (39)
(39)
8. Acknowledgement
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- M. W. Zwierlein, C. H. Schunck ,C. A. Stan, S. M. F. Raupach and W. Ketterle, “Formation Dynamics of a Fermion Pair Condensate,” Physical Review Letters, Vol. 94, 2005, pp. 180401-180404. doi:10.1103/PhysRevLett.94.180401
- M. W. Zwierlein, C. A. Stan, C. H. Schunck, S. M. F. Raupach, A. J. Kerman andW. Ketterle, “Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance,” Physical Review Letters, Vol. 92, No. 4, 2004, pp. 120403-120406. doi:10.1103/PhysRevLett.92.120403
- T. Bourdel, J. Cubizolles, L. Khaykovich, K. M. F. MagalhãesS. J. J. M. F. Kokkelmans, G. V. Shlyapnikov and C. Salomon, “Measurement of the Interaction Energy near a Feshbach Resonance in a 6Li Fermi Gas,” Physical Review Letters, Vol. 91, No. 2, 2003, Article ID 020402. doi:10.1103/PhysRevLett.91.020402
- C. A. Regal, M. Greiner, S. Giorgini, M. Holland and D. S. Jin, “Momentum Distribution of a Fermi Gas of Atoms in the BCS-BEC Crossover,” Physical Review Letters, Vol. 95, No. 25, 2005, Article ID 250404. doi:10.1103/PhysRevLett.95.250404
- C. A. Regal, M. Greiner and D. S. Jin, “Observation of Resonance Condensation of Fermionic Atom Pairs,” Physical Review Letters, Vol. 92, No. 4, 2004, Article ID 040 403.
- C. J. Pethick and H. Smith, “Relaxation and Collective Motion in Superconductors: A Two-Fluid Description,” Annals of Physics, Vol. 119, No. 1, 1979, pp. 133-169.
- C. J. Pethick, H. Smith and P. Bhattacharyya, “Transport Processes in Superfluid 3He-B at Low Temperatures,” Physical Review B, Vol. 15, No. 7, 1977, pp. 3384-3400. doi:10.1103/PhysRevB.15.3384
- C. J. Pethick and H. Smith, “Generation of Charge Imbalance in a Superconductor by a Temperature Gradient,” Physical Review Letters, Vol. 43, No. 9, 1979, pp. 640- 642. doi:10.1103/PhysRevLett.43.640
- C. J. Pethick and H. Smith, “Charge Imbalance in Nonequilibrium Superconductors,” Journal of Physics C: Solid State Physics, Vol. 13, No. 34, 1980, Article ID 6313. doi:10.1088/0022-3719/13/34/004
- C. J. Pethick, H. Smith and P. Bhattacharyya, “Viscosity and Thermal Conductivity of Superfluid 3He: Low-Temperature Limit,” Physical Review Letters, Vol. 34, No. 11, 1975, pp. 643-646. doi:10.1103/PhysRevLett.34.643
- C. J. Pethick and H. Smith, “Orbital Relaxation in Superfluid 3He near Tc,” Physical Review Letters, Vol. 37, No. 4, 1976, pp. 226-229. doi:10.1103/PhysRevLett.37.226
- C. J. Pethick, H. Smith and T. L. Ho, “Bose-Einstein Condensation in Dilute Gases,” Physics Today, Vol. 56, 2003, pp. 62-63. doi:10.1063/1.1595060
- C. J. Pethick, H. Smith and P. Bhattacharyya, “Exact Results for Transport Properties of Anisotropic Fermi Superfluids near the Transition Temperature,” Journal of Low Temperature Physics, Vol. 23, No. 1-2, 1976, pp. 225- 230. doi:10.1007/BF00117252
- V. P. Mineev and K. V. Samokhin, “Introduction to Unconventional Superconductivity,” CRC Press, 1999.
- P. Nozières and S. Schmitt-Rink, “Bose Condensation in an Attractive Fermion Gas: From Weak to Strong Coup- ling Superconductivity,” Journal of Low Temperature Physics, Vol. 59, 1985, pp. 195-211. doi:10.1007/BF00683774
- L. D. Landau and E. M. Lifshitz, “Quantum Mechanics,” Pergamon, Oxford, 1994.
- J. J. Sakurai, “Modern Quantum Mechanics,” Addison Wesley, Inc., Boston, 1994.
- J. J. Sakurai, “Advanced Quantum Mechanics,” Pearson Education India, New Delhi, 2006.
- A. Heidari, “Principles of Modern Relativistic Quantum Mechanics,” Karvar Company Press, Tehran, 2008.
- T. L. Ho and R. B. Diener, “The Condition for Universality at Resonance and Direct Measurement of Pair Wavefunctions Using rf Spectroscopy,” Condensed Matter, Other Condensed Matter, 2004, arXiv:cond-mat/0405174v2.
- T. L. Ho and R. B. Diener, “52Cr Spinor Condensate: A Biaxial or Uniaxial Spin Nematic,” Physical Review Letters, Vol. 96, 2006, pp. 190405-190408. doi:10.1103/PhysRevLett.96.190405
- T. L. Ho and R. B. Diener, “Fermion Superfluids of Nonzero Orbital Angular Momentum near Resonance,” Physical Review Letters, Vol. 94, No. 9, 2005, Article ID 090402. doi:10.1103/PhysRevLett.94.090402
- T. L. Ho and R. B. Diener, “Projecting Fermion Pair Condensates into Molecular Condensates,” Condensed Matter, Superconductivity, 2004, arXiv:cond-mat/0404517v1.
- T. L. Ho and R. B. Diener, “Fermions in Optical Lattices Swept across Feshbach Resonances,” Physical Review Letters, Vol. 96, 2006, Article ID 010402.
- T. L. Ho and R. B. Diener, “Quantum Spin Dynamics of Spin-1 Bose Gas,” Condensed Matter, Other Condensed Matter, 2006, arXiv:cond-mat/0608732v1.
- T. L. Ho and R. B. Diener, “Fermions in Optical Lattices across Feshbach Resonance,” Condensed Matter, Other Condensed Matter, 2005, arXiv:cond-mat/0507253v1.
- [27] M. E. Gehm, S. L. Hemmer, S. R. Granade, K. M. O’Hara and J. E. Thomas, “Mechanical Stability of a Strongly Interacting Fermi Gas of Atoms,” Physical Review A, Vol. 68, 2003, Article ID 011401(R). doi:10.1103/PhysRevA.68.011401
- P. G. De Gennes, “Superconductivity of Metals and Alloys,” W. A. Benjamin, Inc., New York, 1966.
- L. Pitaevski and S. Stringar, “Bose-Einstein Condensation,” Clarendon, Oxford University Press, Oxford, 2003.
- N. D. Mermin, “d-Wave Pairing near the Transition Temperature,” Physical Review A, Vol. 9, No. 2, 1974, pp. 868- 872. doi:10.1103/PhysRevA.9.868
NOTES
*Corresponding author.

