Journal of Modern Physics
Vol. 2 No. 12 (2011) , Article ID: 16502 , 7 pages DOI:10.4236/jmp.2011.212178
Influence of Characteristics of Substance on Parameters of Interaction of Photons High Energy with Free Electrons
Department of Physics, Samara State University, Samara, Russia
E-mail: volobuev@samaramail.ru
Received September 16, 2011; revised October 19, 2011; accepted November 12, 2011
Keywords: Photons, Electrons, Interaction, Not coherent scattering, Compton effect, Substance
ABSTRACT
Various variants of interaction of photons high energy with free electrons in substance are investigated. It is shown, that among these variants, in substance can be observed: absorption of a photon by electron, coherent and not coherent scattering of photons, a stop electron after interaction with a photon. Dependence of change of length of a wave of a photon after interaction with electron from parameters of substance and speed of movement electron is found.
1. Introduction
Interaction of photons and free electrons in substance it is problem known enough. One of results of such interaction, for example, is not coherent scattering. Compton effects or not coherent scattering of X-rays on electrons, poorly connected with a nucleus, at an irradiation of a paraffin surface, which was primarily observed by Compton, is well studied problem [1]. In a spectrum of scattered radiation he observed lower frequency, than frequency of falling radiation. Compton effects represent an example of the quantum nature of light since there is no classical analogue of this phenomenon which could be described Maxwell equations.
There are attempts to describe Compton effects on the basis of wave Doppler effects [2]. Thus electron it is primary considered as the mobile receiver of a wave, and then as a mobile source of a wave. However Compton criticized similar attempts [3]. We shall mark, that the scattering on motionless electron, that in strict mathematical sense it is Compton effects, in general it is not put down in the given model.
Rather detailed analysis of Compton effects is present in [4]. But the analysis [4] is directed on research of effective sections of interaction of electrons and photons. Besides the analysis of Compton effects is carried out in the assumption of is absence of influence of surrounding medium on process.
The purpose of the research is the analysis, first of all, not coherent shift of frequency of a photon and possible results, at interaction of a photon and free electron in substance, and also influence of characteristics of substance on the processes.
Let’s use the method applied in [5] at research of interaction of photons of electromagnetic radiation with binding electrons.
2. Laws of Interaction of a Photon with Free Electron
Let’s consider interaction moving electron with a photon, Figure 1. In all further transformations we believe, that the system of readout is connected to motionless nodes of a crystal lattice of substance.
The law of conservation of energy at interaction of a photon with moving electron we shall write down as:
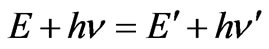 , (1)
, (1)
where Е and Е' is energy of electron before interaction with a photon, h is Planck’s constant, n and n'-the frequency of a photon before and after interaction with electron.
Impulse of a photon before interaction with electron is
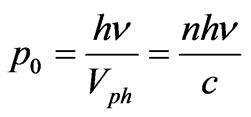 , where
, where  is a speed of a photon in substance,
is a speed of a photon in substance,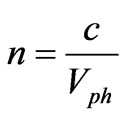 —an absolute index of refraction of substance, c—speed of light in vacuum.
—an absolute index of refraction of substance, c—speed of light in vacuum.
Hence, the formula (1) will be copied as:
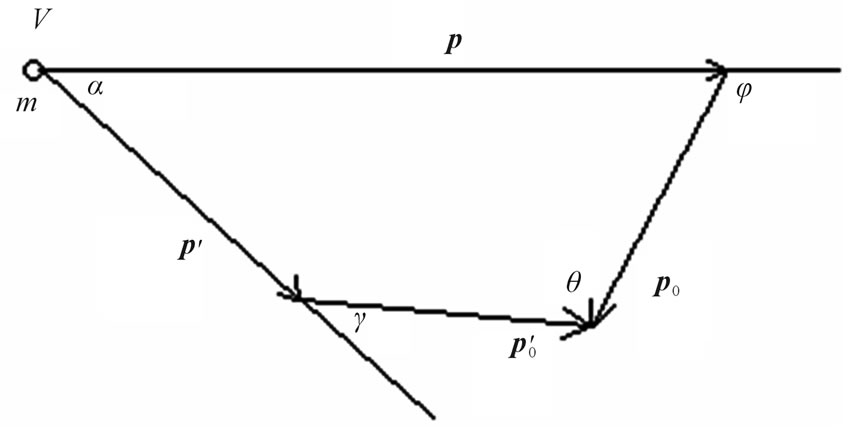
Figure 1. Direction of vectors of impulses of particles at interaction of a photon with free electron.
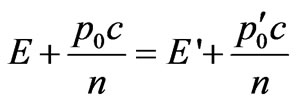 , (2)
, (2)
where  is an impulse of a photon after interaction with electron.
is an impulse of a photon after interaction with electron.
The law of preservation of an impulse before interaction, Figure 1, looks like:
 . (3)
. (3)
Let’s transform (3) to the scalar form:
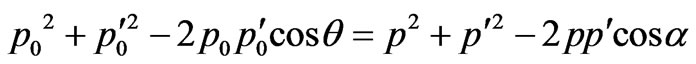 (4)
(4)
where a is an angle between directions of an electron impulse before interaction with a photon, q is an angle between impulses of falling and scattered photons.
Using connection between energy and speed of electron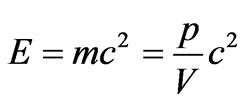 , where
, where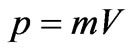 , sizes m and Vmass and speed of electron before interaction, we shall transform the Equation (1) to a kind:
, sizes m and Vmass and speed of electron before interaction, we shall transform the Equation (1) to a kind:
 . (5)
. (5)
In the formula (5)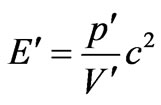 , and V' is electron’s speed after interaction with a photon.
, and V' is electron’s speed after interaction with a photon.
Let’s exclude from (4) and (5) value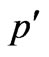 . Finding from (5) value
. Finding from (5) value 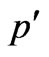 and inserting it in (4), we shall receive:
and inserting it in (4), we shall receive:
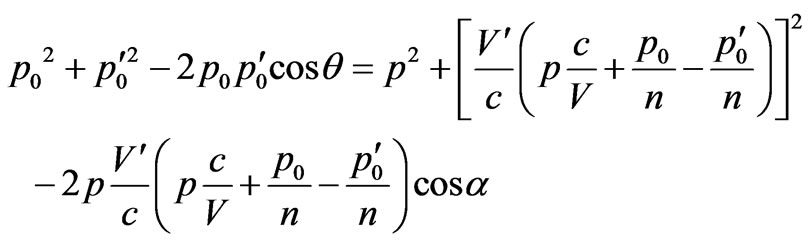 (6)
(6)
Let’s exclude from (6) electron’s speed V' after interaction with a photon. By definition of an impulse of a particle we have:
 , (7)
, (7)
where 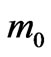 is a rest mass of electron.
is a rest mass of electron.
Inserting (7) into (5), we shall find:
 . (8)
. (8)
Solving (8) be relative V', we have:
 . (9)
. (9)
Inserting (9) into (6), we shall find:
 (10)
(10)
The law of preservation of an impulse (3) in the scalar form can be written down differently, than (4):
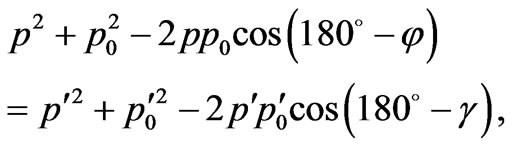 (11)
(11)
or:
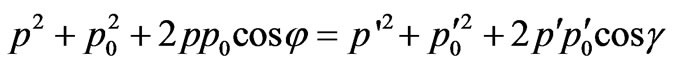 , (12)
, (12)
where j is an angle between directions of movement electron and a photon before interaction, g - is an angle between directions electron and a photon after interaction.
As well as in the previous case, inserting value 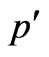 from (5) into (12), we have:
from (5) into (12), we have:
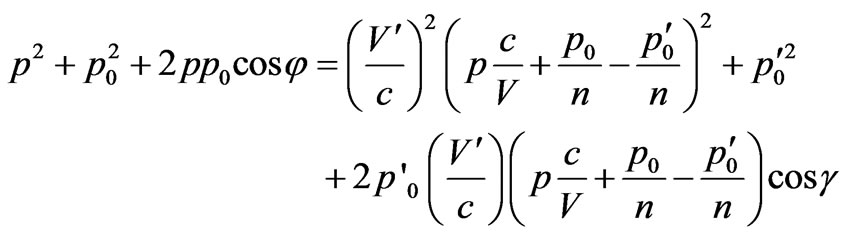 (13)
(13)
Further, using (9), we shall copy (13) as:
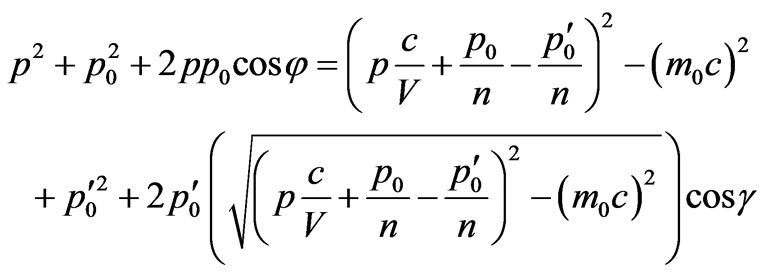 (14)
(14)
Let’s consider some special cases of transformation (10) and (14) which are not excessively cumbersome, and allow to lead the analysis of results obviously enough.
3. Absorption of a Photon by Moving Free Electron
Let’s we assume, that a photon falling on moving free electron, it is completely absorbed. Thus the condition 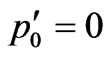 should satisfy. From (14) we find:
should satisfy. From (14) we find:
 . (15)
. (15)
Carrying out transformations, we shall receive:
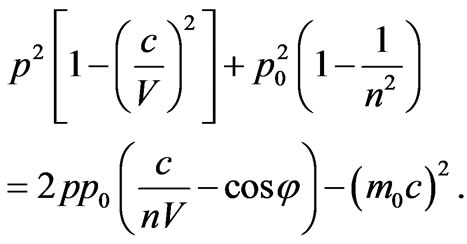 (16)
(16)
Using a formula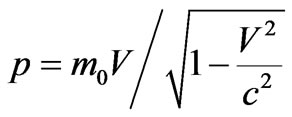 , we have:
, we have:
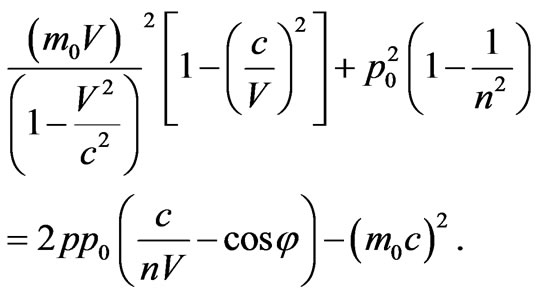 (17)
(17)
It is possible to see, that the first addend in the left part (17) is equal . Hence:
. Hence:
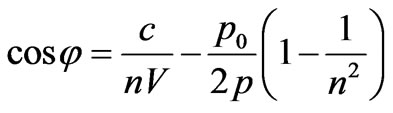 . (18)
. (18)
The received expression is analogue of the formula for an angle of the radiated photon, uniformly moving in medium electron in Vavilov’s—Cherenkov’s effect [6]. Difference is only in a sign a minus in the right part (18) that it is connected to change of a direction of a photon impulse .
.
From the formula (18) follows, that in vacuum, i.e. at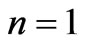 , free electron cannot to absorb a photon, since
, free electron cannot to absorb a photon, since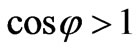 . But in substance, at a condition:
. But in substance, at a condition:
 , (19)
, (19)
such process is possible.
Let’s consider in more detail a condition of absorption of a photon by electron. We shall transform:
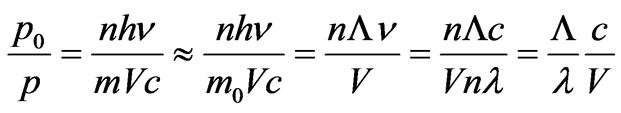 , (20)
, (20)
where size 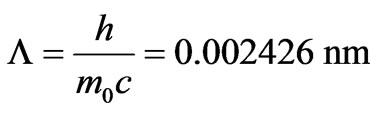 is Compton’s length of an electron wave. It is accepted also, that speed of electron is much less than speed of light in vacuum, so
is Compton’s length of an electron wave. It is accepted also, that speed of electron is much less than speed of light in vacuum, so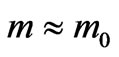 . Hence, the formula (19) becomes:
. Hence, the formula (19) becomes:
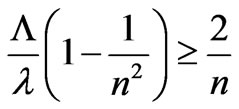 . (21)
. (21)
For 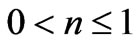 an inequality (19) and (21) it is not correct. If an index of refraction
an inequality (19) and (21) it is not correct. If an index of refraction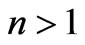 , we receive:
, we receive:
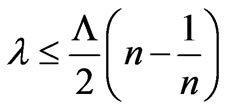 . (22)
. (22)
The formula (22) shows, that absorption of a photon, moving in substance with an index of refraction 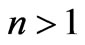 free electron it is possible, probably, only for X-ray radiation. And, the more a index of refraction, the bigger length of a wave can to absorb electron.
free electron it is possible, probably, only for X-ray radiation. And, the more a index of refraction, the bigger length of a wave can to absorb electron.
For lines of the substances resulted in [7], index of refraction for X-ray radiation is less unit, and it is very close to unit. The vacuum for X-ray radiation is in comparison with these substances optically is large dense medium. For X-ray radiation absorption of photons by electron according to (22) is impossible. However, there are no physical bases to deny existence of substances with a index of refraction to more unit for X-ray radiation. Free electrons in such substances could absorb photons of X-ray radiation.
4. Scattering of a Photons on Free Electron
1) Coherent scattering Coherent scattering of a photon on moving free electron arises, if the condition  is observed. The formula (5) will be transformed to a kind
is observed. The formula (5) will be transformed to a kind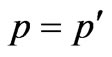 , i.e. electron changes only a direction of the movement. In this case the equation (4) have form:
, i.e. electron changes only a direction of the movement. In this case the equation (4) have form:
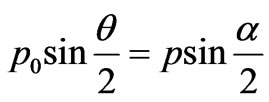 . (23)
. (23)
The Equation (12) results to a condition:
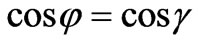 . (24)
. (24)
The condition (24) shows, there are 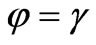 at coherent scattering. The given condition actually is the law of reflection of the photon, similar to the law of reflection of light from mirror interface of two media.
at coherent scattering. The given condition actually is the law of reflection of the photon, similar to the law of reflection of light from mirror interface of two media.
Formulas (23) and (24) also show, that at coherent scattering the quadrangle of impulses on Figure 1 to become symmetric, Figure 2.
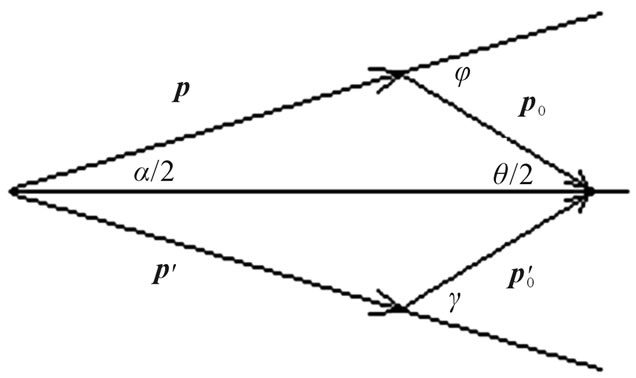
Figure 2. Direction of vectors of impulses of particles at coherent scattering of a photon on free electron.
2) Compton effect Parameters of Compton effect are provided that electron is motionless [6], i.e.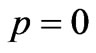 ,
, 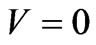 ,
,
 .
.
In this case the formula (10) becomes:
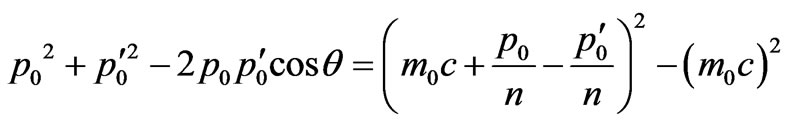 . (25)
. (25)
Carrying out the further transformations (25), we find:
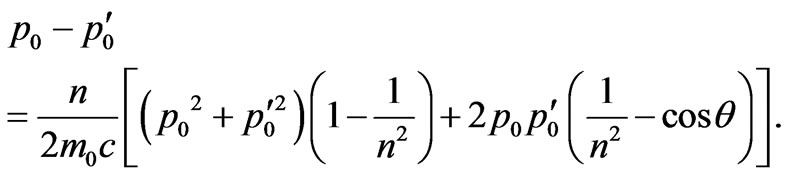 (26)
(26)
Adding and subtracting unit in brackets of last addend (26), we shall receive:
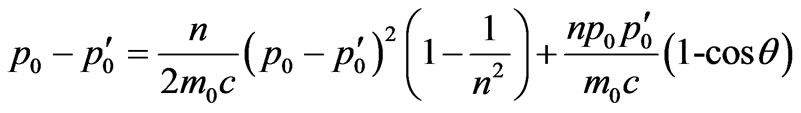 . (27)
. (27)
Let’s designate a difference of impulses falling and scattered photons on electron in vacuum [8]:
 . (28)
. (28)
Thus, the formula (27) can be written down as:
 , (29)
, (29)
where  a difference of impulses falling and scattered photons on electron in substance.
a difference of impulses falling and scattered photons on electron in substance.
Let’s designate dimensionless differences of photons impulses 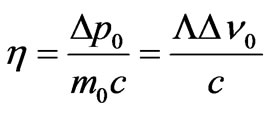 in substance and
in substance and
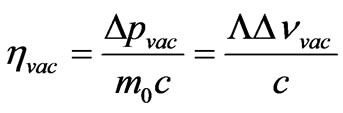 in vacuum. Values
in vacuum. Values 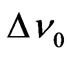 and
and
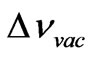 is change of frequency at scattering of a photon, accordingly, in substance and in vacuum.
is change of frequency at scattering of a photon, accordingly, in substance and in vacuum.
In new designations the equation (29) can be copied:
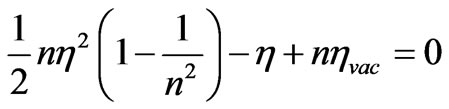 . (30)
. (30)
Solving a quadratic equation (30), we find:
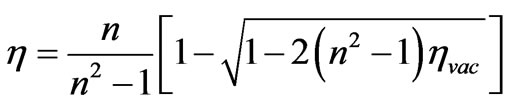 . (31)
. (31)
The sign plus before a root is unacceptable, since in this case differences of photons impulses in substance and in vacuum have a different directivity of change. As it will be from the further, to use in (31) expansion of a root as  is not informatively for the analysis of influence of characteristics of substance on not coherent scattering of a photon.
is not informatively for the analysis of influence of characteristics of substance on not coherent scattering of a photon.
Let’s find in an obvious form change of length of photons wave at their not coherent scattering. We shall transform values:
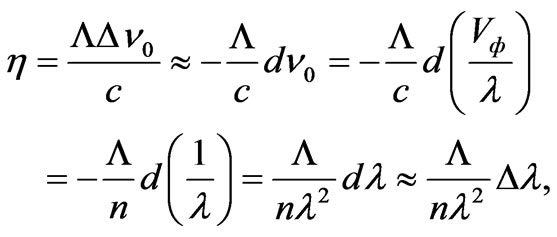 (32)
(32)
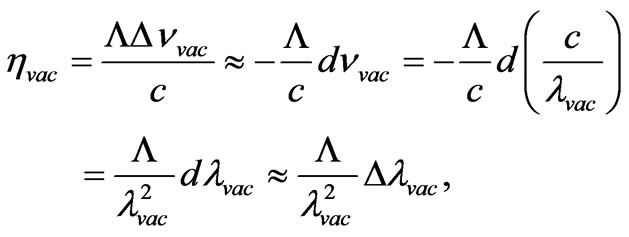 (33)
(33)
where l and  is a lengths of photons waves at it scattering on electrons in substance and in vacuum. Signs a minus are connected by that values
is a lengths of photons waves at it scattering on electrons in substance and in vacuum. Signs a minus are connected by that values  and
and 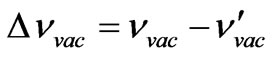 used positive. Besides it is designated
used positive. Besides it is designated 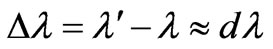 and
and 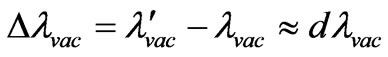 where dashes mean lengths of photons waves after interaction with electron.
where dashes mean lengths of photons waves after interaction with electron.
Using determination of an index of refraction as
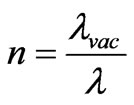 [7], we shall transform (33) to a form:
[7], we shall transform (33) to a form:
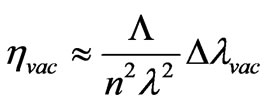 , (34)
, (34)
Inserting (32) and (34) into (31), we’ll find:
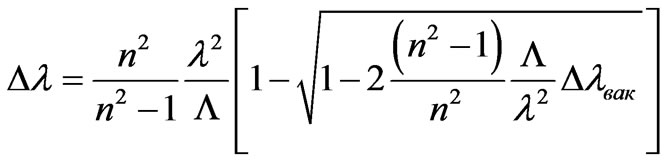 . (35)
. (35)
In expansion of a root in the formula (35) up to the first order we have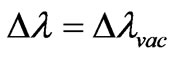 , therefore it is necessary to execute the expansion up to the second order
, therefore it is necessary to execute the expansion up to the second order
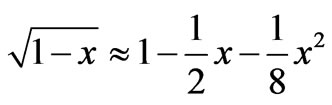 . In result we shall find:
. In result we shall find:
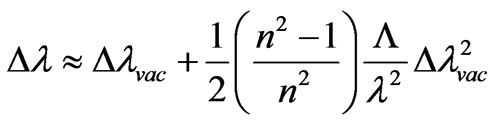 , (36)
, (36)
where , for example, [1].
, for example, [1].
Thus, in the second order of expansion (35) change of length of a wave at not coherent scattering depends from the length of a wave.
Let’s note, that in X-ray area of a spectrum of radiation an index of refraction is . Therefore, according to (36)
. Therefore, according to (36)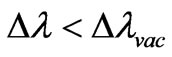 .
.
Let’s designate, following [7], unit decrement of an index of refraction . Then the formula (36) will be transformed to a form:
. Then the formula (36) will be transformed to a form:
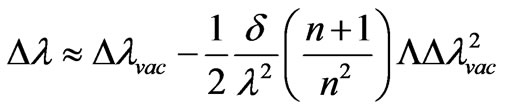 . (37)
. (37)
The index of refraction of substances in a X-ray range is close to unit [7], therefore the formula (37) can be copied as follows:
 . (38)
. (38)
The formula (38) shows, that in a X-ray range influence of substance on parameters of not coherent scattering is very insignificant and at practical calculations it is possible to use classical formula of Compton 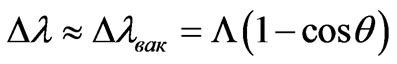 . The opportunity of use of Compton formula in substance mathematical is determined by that expansion (35) up to the first order parameters of substance is absent.
. The opportunity of use of Compton formula in substance mathematical is determined by that expansion (35) up to the first order parameters of substance is absent.
Proceeding from the classical theory of a Lorentz dispersion [7], we have in a X-ray range dependence
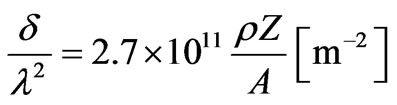 , where
, where 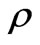 is density of substance in kg/m3, Z is charging number, A is mass number. Using
is density of substance in kg/m3, Z is charging number, A is mass number. Using , we find:
, we find:
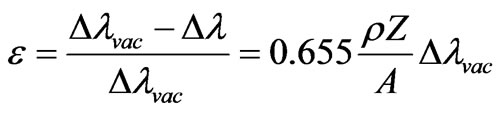 . (39)
. (39)
Relative change of shift of wave length e in substance in comparison with vacuum at not coherent scattering in a X-ray range of a spectrum of electromagnetic radiation is proportional to density of substance, its charging number and in inverse proportion to nuclear mass of substance. It also linearly depends from Compton’s shift of length of a wave in vacuum.
5. The Stop of Free Electron after Interaction with Photon
Let’s find conditions at which free electron after interaction with a photon in substance will be stop, i.e.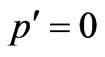 .
.
In this case the equation (5) gets a form:
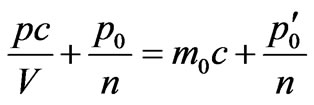 . (40)
. (40)
From the Equation (40) we’ll find:
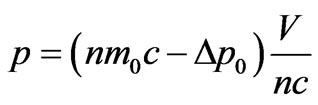 , (41)
, (41)
where, as before,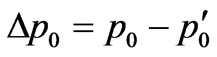 .
.
Formulas (4) and (12) change:
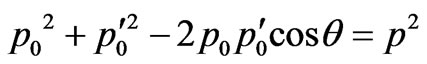 , (42)
, (42)
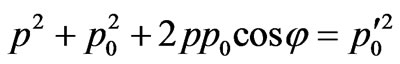 . (43)
. (43)
Using  the equation (43) it is possible to transform to a form:
the equation (43) it is possible to transform to a form:
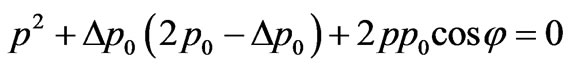 . (44)
. (44)
Solving in common (42) and (43) we shall find:
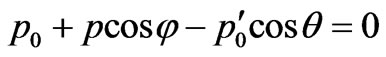 , (45)
, (45)
that is equivalent:
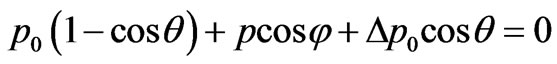 . (46)
. (46)
Finding from (46) value  and inserting it in (44), we have:
and inserting it in (44), we have:
 (47)
(47)
Transform (47), we’ll find:
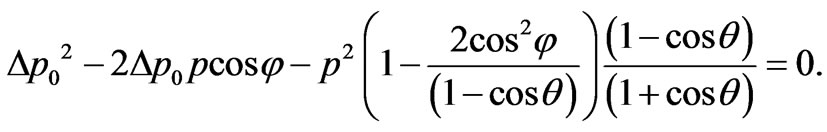 (48)
(48)
Solving a quadratic Equation (48), we find:
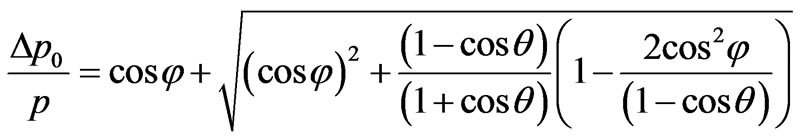 . (49)
. (49)
As it will be shown below, before a root it is necessary to take a sign plus.
After simple transformations of the formula (49), we shall find:
 . (50)
. (50)
The formula (50) shows, that at a head-on interaction of a photon and moving electron, i.e. at 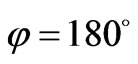 in case if electron after interaction stops, a direction of an scattered photon equiprobably in all directions. The sign plus before a root in the formula (49) is connected with geometrical interpretation of the formula (50), Figure 3.
in case if electron after interaction stops, a direction of an scattered photon equiprobably in all directions. The sign plus before a root in the formula (49) is connected with geometrical interpretation of the formula (50), Figure 3.
Let’s marked, that in case if electron after interaction with a photon does not stop, the formula (50) according to the similar simple geometrical analysis Figure 1, has more a general form:
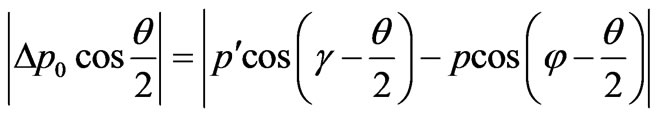 . (51)
. (51)
At use (41) formula (50) will be transformed to a form:
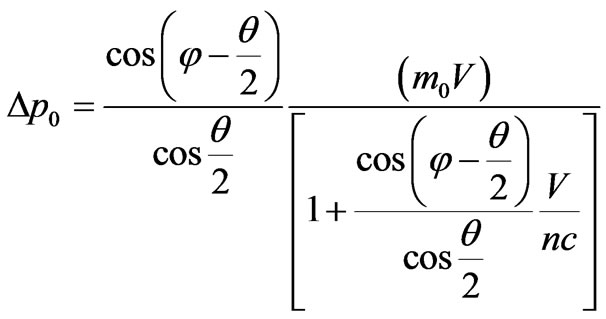 . (52)
. (52)
Similarly (32), we shall pass from change of an impulse of photons 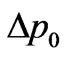 to the shift of lengths of waves:
to the shift of lengths of waves:
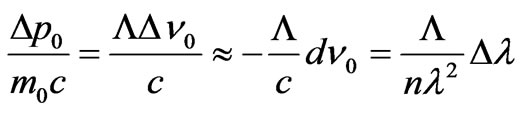 . (53)
. (53)
Hence, from (52) we shall find:
 . (54)
. (54)
The formula (54) is a special case of not coherent scattering when electron on which there is a scattering, after interaction with a photon stops. Energy of movement electron is transferred an scattered photon, therefore its frequency increases, and the length of a wave
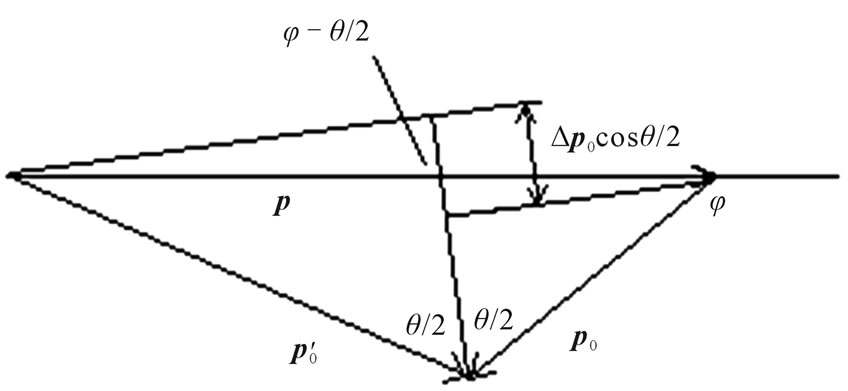
Figure 3. Geometrical interpretation of interaction of a photon with stopping electron.
decreases on value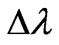 .
.
As considered the case when electron stops, an angle is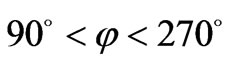 , Figure 3. Average value of angle j takes place in case of a head-on interaction of X-ray photon (
, Figure 3. Average value of angle j takes place in case of a head-on interaction of X-ray photon (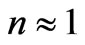 ) and electron, therefore further we shall be limited to this case. At
) and electron, therefore further we shall be limited to this case. At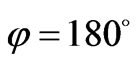 , we have:
, we have:
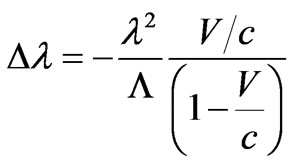 . (55)
. (55)
The sign a minus specifies on reduction of length of a wave after interaction of a photon with stopping electron.
Let’s note, that the formula (55), really, can lead to idea—describe Compton effect by Doppler’s shift of length of a wave [2]. However, dependence of shift of length of a wave from angle q in the formula (54) differs from its in [2] which, proceeding from Doppler effect is received as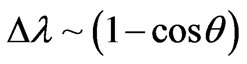 .
.
Change of shift of lengths of waves due to movement of electrons at not coherent scattering, taking into account (55), is equal:
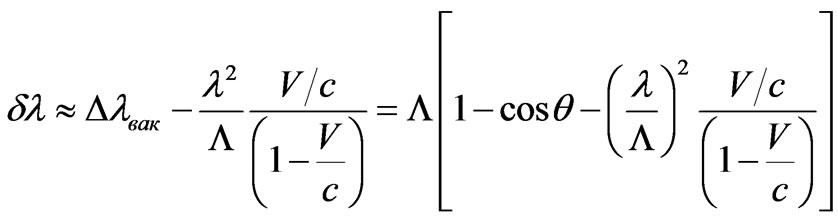 .(56)
.(56)
On Figure 4 the curve of dependence of shift 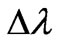 for not coherent line of scattered radiation from angle q [7] is shown. The experimental points received for carbon at length of a wave of radiation
for not coherent line of scattered radiation from angle q [7] is shown. The experimental points received for carbon at length of a wave of radiation 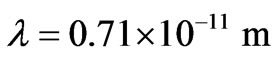 are shown also. From the analysis of curves follows, that at angle q close to 180˚ rather big reduction of shift
are shown also. From the analysis of curves follows, that at angle q close to 180˚ rather big reduction of shift 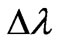 is observed. This reduction can be explained only by movement of electron, since from the formula (37) cannot get
is observed. This reduction can be explained only by movement of electron, since from the formula (37) cannot get
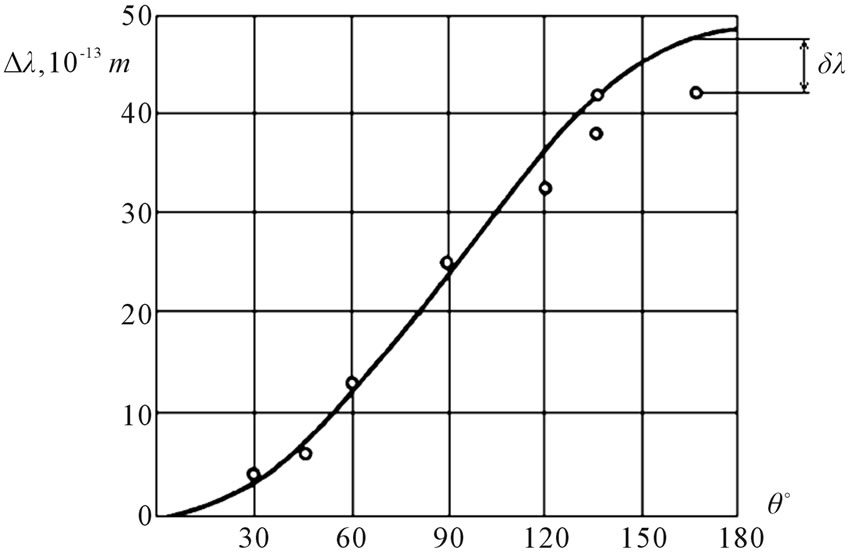
Figure 4. Experimental dependence of shift of not coherent line of scattered X-ray radiation from an angle of scattering of photons q. Continuous line is calculation under formula of Compton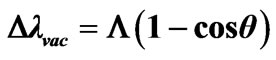 .
.
such big reduction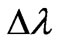 . Delay of movement of electron at interaction with a photon results to increase of energy of a scattered photon, i.e. reduction value
. Delay of movement of electron at interaction with a photon results to increase of energy of a scattered photon, i.e. reduction value 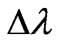 on size
on size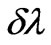 . The estimation which has been carried out under the formula (56) shows, that value
. The estimation which has been carried out under the formula (56) shows, that value 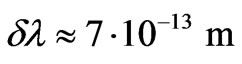 observable in experiment at an angle
observable in experiment at an angle 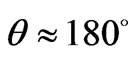 arises at initial speed of electron
arises at initial speed of electron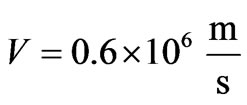 . This speed is close to speed to Fermi for electron which can be analogue of speed of thermal movement of electronic gas [9].
. This speed is close to speed to Fermi for electron which can be analogue of speed of thermal movement of electronic gas [9].
Calculation under the formula (56), obviously, has estimated character. First, there is thermal distribution Fermi-Dirac of speeds of electronic gas in substance, therefore photons are necessary for a stop of electrons must be various energy. Second, the head-on interaction of photons and electrons is enough rare. Thirdly, the stop of electron after interaction with a photon also is occurrence enough rare. In a general change of an impulse of a photon at not coherent scattering is determined by the law (51). Strictly speaking stop in electronic gas two electrons can only with various directions spin. It follows from a principle of veto of Pauli. Hence, there should be a statistical distribution of size  which is stochastic ways form of its numerical value. However, taking into account, that the head-on interaction of a photon and electron is observed, when angle j achieves average value 180˚ in considered process (
which is stochastic ways form of its numerical value. However, taking into account, that the head-on interaction of a photon and electron is observed, when angle j achieves average value 180˚ in considered process (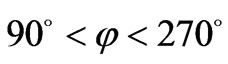 ), and also close to speed of electron under the formula (56) to speeds of Fermi, it is possible to assume that an estimation of size
), and also close to speed of electron under the formula (56) to speeds of Fermi, it is possible to assume that an estimation of size 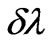 under this formula is allowable at angle q close to 180˚.
under this formula is allowable at angle q close to 180˚.
6. Conclusions
At interaction of a photon with free electron in substance various results are possible: absorption of a photon, coherent and not coherent scattering, a stop of electron.
Thus absorption of a photon in a X-ray range probably only in substance with an index of refraction is more than unit.
Change of length of a wave at not coherent scattering of X-ray radiation in substance in the second order depends from the length of a wave, as against not coherent scattering in vacuum. Influence of parameters of substance: density, charging and mass numbers on shift of lengths of waves of falling and scattered radiations very insignificantly.
Observable reduction of shift of lengths of waves at not coherent scattering can be explained only by movement of free electrons, interacting with photons. At a head-on interaction of a photon and moving electron in case electron after interaction stops, a direction of a scattered photon equiprobably in all directions.
REFERENCES
- E. H. Wichmann, “Quantum Physics,” Science, Moscow, 1977, p. 156.
- R. Kidd, J. Ardini and A. Anton, “Compton Effect as a Double Doppler Shift,” American Journal of Physics, Vol. 53, No.7, 1985, p. 641. doi:10.1119/1.14274
- A. H. Compton, “Secondary Radiations Produced by XRays,” The National Research Council of the National Academy of Sciences, Washington, DC, 1922, pp. 18-20.
- V. B. Berestetsky, E. M. Lifshits and L. P. Pitaevskij, “Quantum Electrodynamics,” Science, Vol. 4, 1989, p. 402.
- A. N. Volobuev and E. S. Petrov, “Angular Distribution of Photoelectrons during Irradiation of Metal Surface by Electromagnetic Wave,” Journal of Modern Physics, Vol. 2, No. 8, 2011, pp. 780-786. doi:10.4236/jmp.2011.28091
- V. G. Levich, “The Course of Theoretical Physics,” PhysMathGiz, Vol. 1, 1962, pp. 246-302.
- M. A. Blohin, “Physics of Roentgen Rays,” State Publishing House, Moscow, 1957, pp. 192-301.
- A. N. Matveev, “Nuclear Physics,” The Higher School, Moscow, 1989, p. 27.
- N. Ashcroft and N. Mermin, “Solid-State Physics,” Holt, Rinehart and Winston, New York, 1976, p. 49.

