Journal of Modern Physics
Vol.3 No.6(2012), Article ID:20095,4 pages DOI:10.4236/jmp.2012.36061
Positive Magnetoresistance in Hydrogenated Amorphous Alloys Silicon Nickel a-Si1–yNiy:H at Very Low Temperature with Magnetic Field
1Research Group ESNPS, Physics Department, Faculty of Sciences, University Ibn Zohr, Agadir, Morocco
2Laboratoire de Physique de la Matière Condensée, Département de Physique, Faculté des Sciences et Techniques de Mohammadia, Mohammedia, Morocco
3Laboratoire de Spectroscopie Hertzienne LSH, Université de LilleI, Villeneuve d’Ascq Cedex, France
Email: *kaaouachi21@yahoo.fr
Received September 12, 2011; revised September 30, 2011; accepted October 25, 2011
Keywords: Amorphous silicon-nickel alloys a-Si1–yNiy:H; Variable Range Hopping Conductivity; Metal insulator transition; positive magnetoresistance
ABSTRACT
We present results of an experimental study of magnetoresistance phenomenon in an amorphous silicon-nickel alloys a-Si1–yNiy:H (where y = 0.23) on the insulating side of the metal-insulator transition (MIT) in presence of magnetic field up to 4.5 T and at very low temperature. The electrical resistivity is found to follow the Efros-Shklovskii Variable Range Hopping regime (ES VRH) with T–1/2. This behaviour indicates the existence of the Coulomb gap (CG) near the Fermi level.
1. Introduction
In Variable Range Hopping (VRH) of the three dimensional disordered systems, like doped semiconductors, The resistivity ρ was shown by Mott [1,2] to behave like exp(T0/T)1/4. This dependence was obtained by optimizing the hopping probability and assuming a slowly varying Density of State (DOS) in the vicinity of the Fermi level.
On the contrary, Efros and Shklovskii (ES) [3,4] have predicted that range electron-electron interaction reduces the DOS at the Fermi level and creates a soft Coulomb Gap (CG), which takes the form , A is a constant and
, A is a constant and . The existence of the CG leads to the ES VRH regime of the resistivity, which behaves like exp(T0/T)1/2.
. The existence of the CG leads to the ES VRH regime of the resistivity, which behaves like exp(T0/T)1/2.
The VRH regime leads to the following temperature behaviour of resistivity:
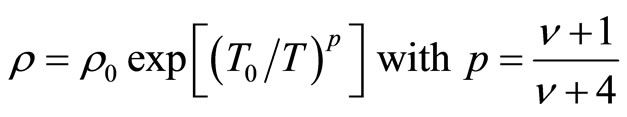 (1)
(1)
Equation (1) remains quite universal since when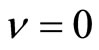 , the DOS is constant and p = 0.25 corresponding to the Mott regime. But when
, the DOS is constant and p = 0.25 corresponding to the Mott regime. But when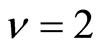 , the DOS varies in the vicinity of the Fermi level and p = 0.5. The experimental situation has been confusing for some times, with both values being observed. Mott VRH and ES VRH have been widely observed in many doped semiconductors [5-9].
, the DOS varies in the vicinity of the Fermi level and p = 0.5. The experimental situation has been confusing for some times, with both values being observed. Mott VRH and ES VRH have been widely observed in many doped semiconductors [5-9].
The metal-insulator transition in amorphous alloys has been an active field of experimental investigations over recent years, particularly in alloys of silicon and germanium [10-13].
Experimental results on resistivity in amorphous alloy a-Si0.77Ni0.23:H at low temperature and with magnetic field, have been analyzed in the insulating side of the metal-insulator transition (MIT). The positive magnetoresistance (PMR) measurements were obtained in the range of temperature 1 - 4.2 K and with magnetic field up to 4.5 T.
The sample was prepared by radio-frequency sputtering from silicon target. The substrate (Corning 7059 glass) was at room temperature during deposition and the sputtering gas was a 90% Ar and 10% H2. The hydrogen was added to saturate silicon dangling bonds that might caused by the disorder.
Film thickness which was about 1 µm, was measured to an accuracy of 0.1 µm using a Talysurf stylus. The amorphous nature was demonstrated by electron diffraction measurements in a transmission electron microscope.
The electrical resistivity was measured using standard four-terminal AC techniques.
In Figure 1, we plot the magnetoresistance (∆ρ/ρ0) versus magnetic field. We noticed that it is positive and increases when the temperature decreases. ρ0 is the resistivity at B = 0 T.
2. Theoretical Models of Positive Magnetoresistance in the VRH Regime
The theory, both for a constant density of states at the Fermi level and also for an arbitrary power-law dependence of N(EF), has been developed by Shklovskii and Efros [3] for weak magnetic field and by Tokumoto et al. [14] for high magnetic field. The criterion for the transition between low and high magnetic field regimes is given by:
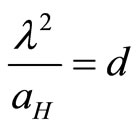 (2)
(2)
where d is the mean distance between impurities, 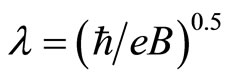 is the magnetic length, and
is the magnetic length, and 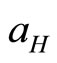 is the electron effective Bohr radius at zero magnetic field. The latter can be calculated using the formula
is the electron effective Bohr radius at zero magnetic field. The latter can be calculated using the formula 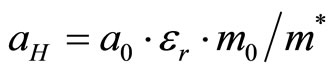 , where
, where 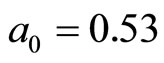 Å and
Å and  is the relative permittivity of the medium.
is the relative permittivity of the medium.
When 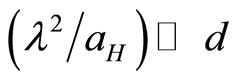 (low magnetic field), Shklovskii and Efros [3] give the following equation of positive magnetoresistance in VRH regime:
(low magnetic field), Shklovskii and Efros [3] give the following equation of positive magnetoresistance in VRH regime:
 (3)
(3)
where  is a constant depending on the form of the density of states and
is a constant depending on the form of the density of states and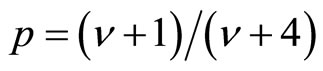 . The parameter
. The parameter
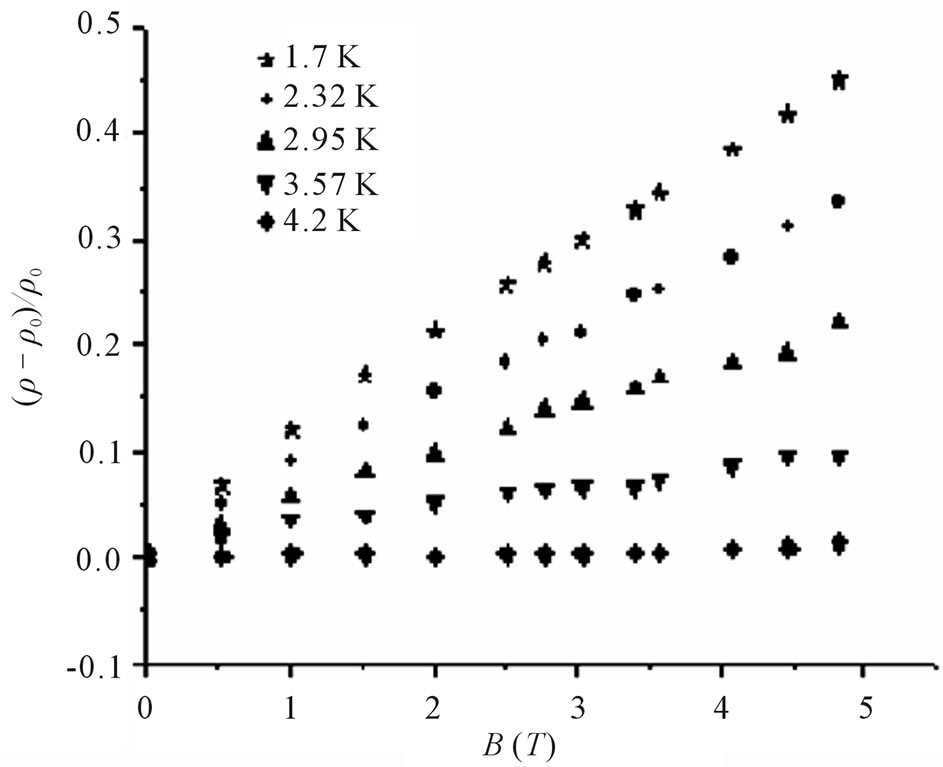
Figure 1. Positive magnetoresistance (∆ρ/ρ0) versus magnetic field B for several values of temperature.
ν is known to be equal to zero (i.e., p = 0.25) when the DOS  is constant near the Fermi level [1,2], whereas, ν = 2 when N(EF) varies, creating the Coulomb gap [3]. The parameter
is constant near the Fermi level [1,2], whereas, ν = 2 when N(EF) varies, creating the Coulomb gap [3]. The parameter 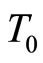 depends on N(EF) and on the localization length
depends on N(EF) and on the localization length  [13,15].
[13,15].
Equation (3) can be simplified as:
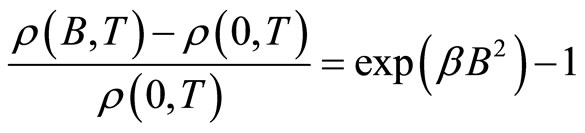 (4)
(4)
The parameter 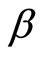 is dependent on the temperature in the VRH regime.
is dependent on the temperature in the VRH regime.
When 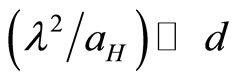 (high magnetic field), Tokumoto et al. [14] give a positive magnetoresistance expression, of the form:
(high magnetic field), Tokumoto et al. [14] give a positive magnetoresistance expression, of the form:
 (5)
(5)
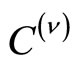 is also a constant depending on the form of the density of states, and
is also a constant depending on the form of the density of states, and 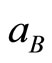 is equal to
is equal to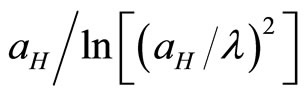 .
.
Equation (5) can be simplified to:
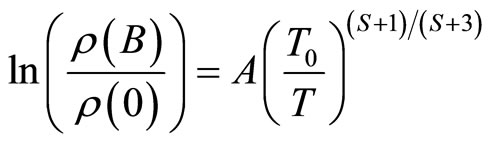 (6)
(6)
where 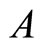 is a constant independent of
is a constant independent of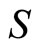 , but varying like B.
, but varying like B.
3. Results and Discussion
Taking 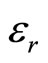 in vicinity of 14 [16],
in vicinity of 14 [16], 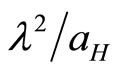 is found to be of order of
is found to be of order of  for B = Bmax = 4.5 T, Whereas the mean Ni-Ni distance
for B = Bmax = 4.5 T, Whereas the mean Ni-Ni distance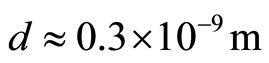 , so that
, so that  throughout the interval of magnetic field 0 - 4.5 T. Thus we can use Equation (3) to study the behaviour of the positive magnetoresistance.
throughout the interval of magnetic field 0 - 4.5 T. Thus we can use Equation (3) to study the behaviour of the positive magnetoresistance.
In Figure 2 we plot  against
against 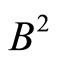 for different temperature. Straight lines with various slopes corresponding to different values of
for different temperature. Straight lines with various slopes corresponding to different values of 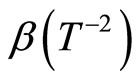 are observed.
are observed.
We have a satisfactory result, if using Equations (3) and (4) for the variation of  against ln(T). Indeed we obtain a straight line with a slope near the value
against ln(T). Indeed we obtain a straight line with a slope near the value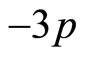 .
.
In Figure 3 we plot 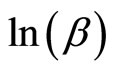 against
against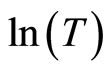 . We find a straight line with negative slope equal to −1.59. This value is to close to −1.5 and we can conclude that we have a ES VRH regime corresponding to
. We find a straight line with negative slope equal to −1.59. This value is to close to −1.5 and we can conclude that we have a ES VRH regime corresponding to 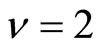 and
and  .
.
The VRH conduction depends essentially on the relative magnitude of the hopping energies of Mott ∆M, of ES ∆ES, and of CG ∆CG. Very close to the MIT, Iqbal et al. [17] showed that the CG becomes so narrow that the temperature range where the ES regime occurs cannot be reached and only the Mott regime is expected. The origin
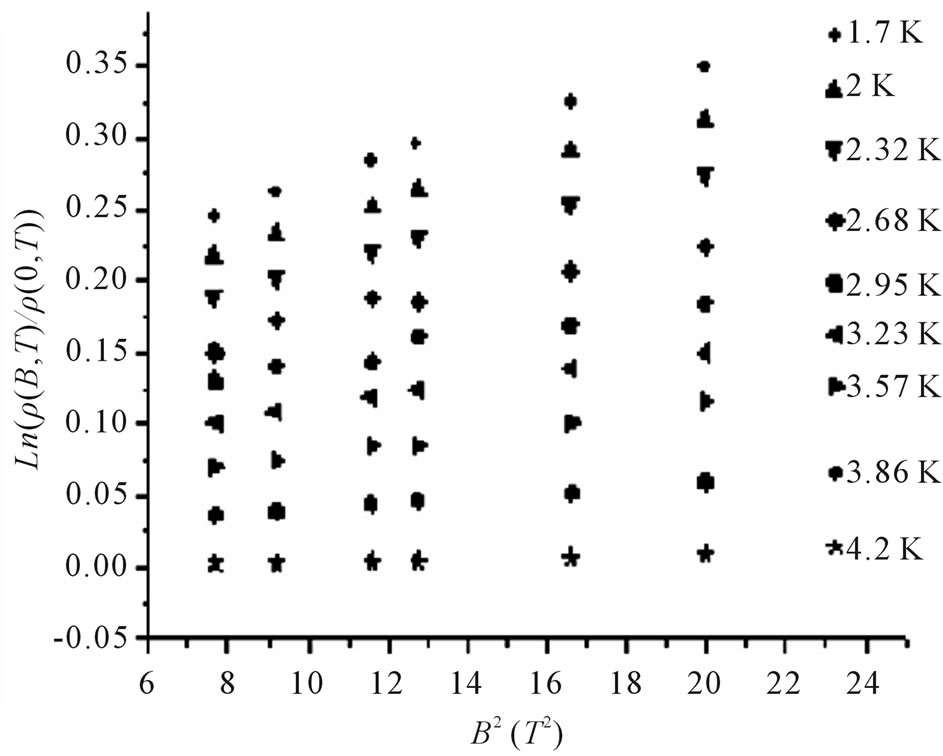
Figure 2. Variation of 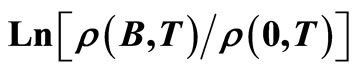 against B2 for several values of temperature.
against B2 for several values of temperature.
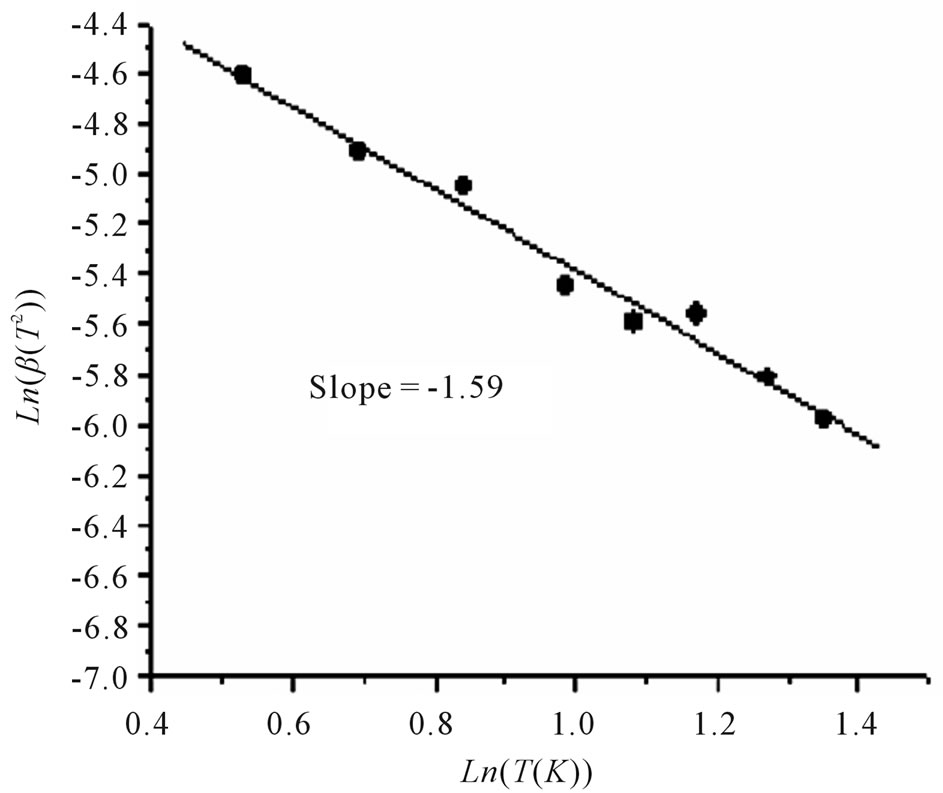
Figure 3.  in Equation (4) against
in Equation (4) against .
.
of the disagreement with our results is quite difficult to explain. Therefore, VRH theories should be developed in the systems that are situated near the MIT.
4. Conclusions
The study of the positive magnetoresistance behaviour can help us to assume an accurate imagination about the density of states in vicinity of the Fermi level by highlighting the VRH regime that governs the electron hopping.
At very low temperature (T < 4.2 K), the electrical conductivity of Si0.77Ni0.23:H shows Efros-Shklovskii VRH that corresponds to nonzero constant density of states at the Fermi level, and demonstrates a positive magnetoresistance at low magnetic field.
The electron-electron interactions still significant even if the Coulomb Gap is narrow near the MIT. No crossover from Efros-Shklovskii to Mott is observed.
5. Acknowledgements
We are grateful to Professor K. M. Abkemeier et al. for using their experimental results on a-Si1-yNiy:H in our investigations.
REFERENCES
- N. F. Mott, “Conduction in Glasses Containing Transition Metal Ions,’’ Journal of Non-Crystalline Solids, vol. 1, No. 1, 1968, pp. 1-17. doi:10.1016/0022-3093(68)90002-1
- Mott, N. F., “Metal-Insulator Transitions,” Taylor and Francis, London, 1974.
- B. I. Shklovskii and A. L. Efros, “Electronic Properties of Doped Semiconductors,” Springer, Berlin, 1984.
- L. Efros and B. I. Shklovskii, “Coulomb Gap and Low- Temperature Conductivity of Disordered Systems,” Journal of Physics C: Solid State Physics, vol. 8, No. 4, 1975, p. 49.
- A. El kaaouachi, A. Nafidi and G. Biskupski, “Positive and Negative Magnetoresistance on Both Sides of the Metal-Insulator Transition in Metallic N-Type InP,” Semiconductors Sciences and Technology, vol. 18, No. 2, 2003, pp. 69-74.
- R. Abdia, A. El kaaouachi, A. Nafidi and J. Himine, “Positive Magnetoresistance Behaviour in the Insulating Side of the Metal-Insulator Transition in CdSe,” Physica B: Condensed Matter, vol. 373, No. 1, 2006, pp. 96-99. doi:10.1016/j.physb.2005.11.096
- A. El kaaouachi, R. Abdia and A. Nafidi, “Positive Magnetoresistance in the Variable Range Hopping Regime in CdSe, Physica E: Low-Dimensional Systems and Nanostructures,’’ Physica E: Low-dimensional Systems and Nanostructures, vol. 32, No. 1-2, 2006, pp. 419- 421.
- R. Abdia, A. El kaaouachi, A. Nafidi, G. Biskupski and J. Hemine, “Variable Range Hopping Conductivity and Negative Magnetoresistance in N-Type InP Semiconductor,” Journal of Solid State Electronics, Vol. 53, No. 5, 2009, pp. 469-472. doi:10.1016/j.sse.2009.02.002
- A. El kaaouachi, R. Abdia, A. Nafidi and G. Biskupski, “Crossover Phenomenon for Variable Range Hopping Conduction and Positive Magnetoresistance in Insulating N-Type InP,’’ Journal of Annales de Chimie Sciences des Matériaux France, Vol. 33, No. 4, 2008, pp. 357-364.
- A. Mobius, “The Metal-Semiconductor Transition in Amorphous Si1−xCrx Films: Phenomenological Model for the Metallic Region,” Zeitschrift Für Physik B Condensed Matter, Vol. 80, No. 2, 1990, pp. 213-223. doi:10.1007/BF01357505
- R. Rosenbaum, A. Heines, A. Palevski, M. Karpovski, A. Gladkikh, M. Pilosof, A. J. Daneshvar, M. R Graham, T. Wright, J. T. Nicholls, C. J. Adkins, M. Witcomb, V. Prozesky, W. Przybylowicz and R. Pretorius, “Metallic Transport Properties of Amorphous Nickel Silicon Films,” Journal of Physics: Condensed Matter, vol. 9, No. 25, 1997, pp. 5395-5411. doi:10.1088/0953-8984/9/25/008
- A. Heinrich, H. Vinzelberg, D. Elefant and C. Gladun, “Conductivity and Agnetoconductivity of Amorphous CrxGe1−x near the Metal-Insulator Transition,” Journal of Non-Crystalline Solids, Vol. 164-166, 1993, pp. 513-516. doi:10.1016/0022-3093(93)90602-T
- S. Yoshizumi, T. H. Geballe, M. Kunchur and W. L. McLean, “Magnetoresistance of amorphous MoxGe1−x near the Metal-Insulator Transition,” Physical Review B, vol. 37, No. 12, 1988, pp. 7094-7097. doi:10.1103/PhysRevB.37.7094
- H. Tokumoto, R. Mansfield and M. J. Lea, “Correlation Effects in Variable-Range Hopping Conduction in NType Indium Antimonide below l K,” Philosophical Magazine Part B, vol. 46, No. 2, 1982, pp. 93-113. doi:10.1080/13642818208246427
- P. Youzou Zang, O. Dai, M. Levy and M. P. Sarachik, “Probind the Colomb Gap in Insulating N-Type CdSe” Physical Review Letters, vol. 64, No. 22, 1990, pp. 2687- 2690. doi:10.1103/PhysRevLett.64.2687
- S. C. Baliss, R. Assal, E. A, Davis and T. West, “OJDOS Evidence for a Semiconductor-to-Metal Transition in a-Si1-yNiy:H,” Journal of Physics: Condensed Matter, vol. 3, No. 7, 1991, pp. 793-800. doi:10.1088/0953-8984/3/7/004
- M. Iqbal, J. Galibert, J. Léotin, S. Askenazy, S. Waffenschmidt and J. Wosnitza, “Coulomb Gap Shrinkage in Compensated Si:(P,B) in High Magnetic Fields,” Physica B: Condensed Matter, vol. 246-247, 1998, pp. 282-285. doi:10.1016/S0921-4526(97)00916-2
NOTES
*Corresponding author.

