ABSTRACT

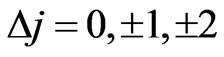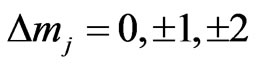Spin dependent selection rules for photonic transitions in hydrogen-like atoms is derived by using the solution of Dirac equation for hydrogen-like atoms. It is shown that photonic transitions occur when [while]. By applying the spin dependent selection rules, we can explain the observed (6 s7 s) transition in Cesium (Cs) atom.

1. Introduction

Applications of hydrogen-like atoms in technology are more than the hydrogen atom itself. Accurate determination of the excited-state properties of atomic and molecular systems, such as fine and hyperfine coupling constants, oscillator strengths play important roles for testing the high-precision atomic theory and quantum mechanics. The aim of the present study is to find spin dependent selection rules for photonic transitions in hydrogen-like atoms. We first derive the spin dependent eigenstates of the hydrogen-like atoms then find a more accurate correspondence between these eigenstates. So far in literature the states have been denoted by the quantum numbers (n, l, j) [1] but not by the quantum numbers (n, l, m_j). In this way, we distinguish the states in the Zeeman sense including the quantum number, m_j. By using the Fermi-Golden rule, we calculate the non-zero matrix elements and then develop the spin dependent selection rules for the photonic transitions in the hydrogen-like atoms. We show that photonic transitions occur when and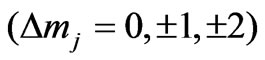. By applying the spin dependent selection rules, we can explain the observed 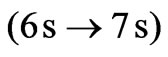transition in Cesium (Cs) atom. The outline of the present study is as follows. In Section 2 we give a short summary of the Dirac hydrogen atom and then extend it to the hydrogen-like atoms. In Section 3 we develop the spin dependent transition rates for Dirac hydrogen-like atoms. In Section 4 we give the explanation of the (6 s - 7 s) transition of Cs in terms of the spin dependent selection rules. In Section 5 we give the conclusions.

2. The Dirac Hydrogen Atom

To find the eigenvalue of the Dirac hydrogen-like atom, we will begin with the Dirac Hamiltonian of the hydrogen atom [2-4]:

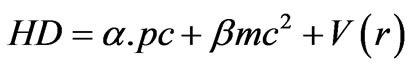(1)

where is the Coulomb potential, m is the mass of an electron, c is the velocity of light, 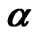and 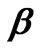are the standard Dirac matrices in the Dirac representation:

(2)

Here the 1's and 0's stand for 2 × 2 unit and zero matrices respectively and the 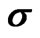is the standard vector composed of the three Pauli matrices. Since the Hamiltonian is invariant under rotations, we look for simultaneous eigenfunctions of H_D, |J|², and J_z, where

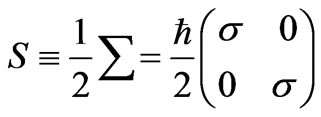(3a)

and J_z = L_z + S_z or m_j = m + m_s(3b)

We remark that the spin operator is diagonal in terms of 2 × 2 Pauli spin matrices; therefore the angular part should be precisely that of the Pauli two-component theory. Defining

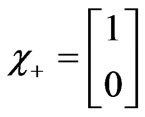and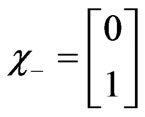

the spin dependent wave functions can be written as [5]:

(4a)

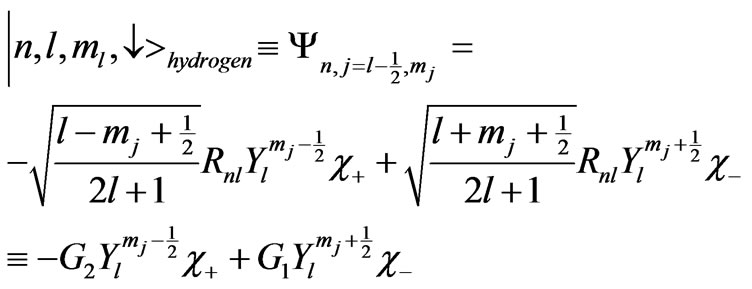(4b)

where 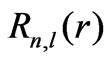is the radial wave function, are the spherical harmonics. Further in Equation (4a), 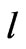can be replaced by (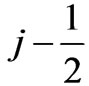) (spin-up case);and in Equation(4b), 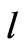can be replaced by 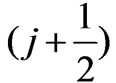(spin-down case). In a hydro-gen-like atom the potential 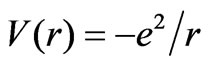is replaced by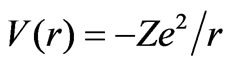, where Z is the atomic number. So the spin dependent eigenfunctions for hydrogen-like atoms are written as:

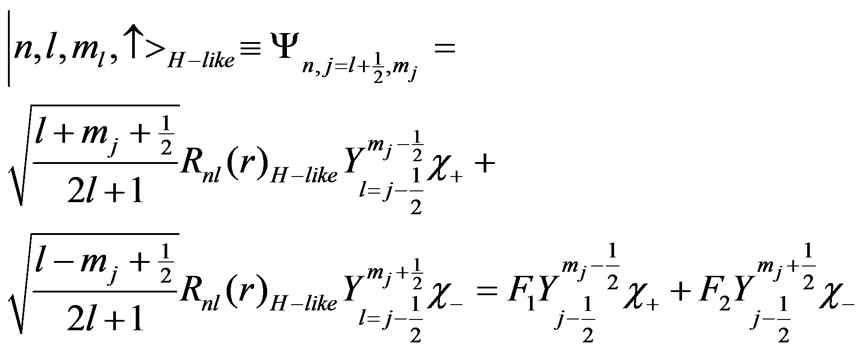(5a)

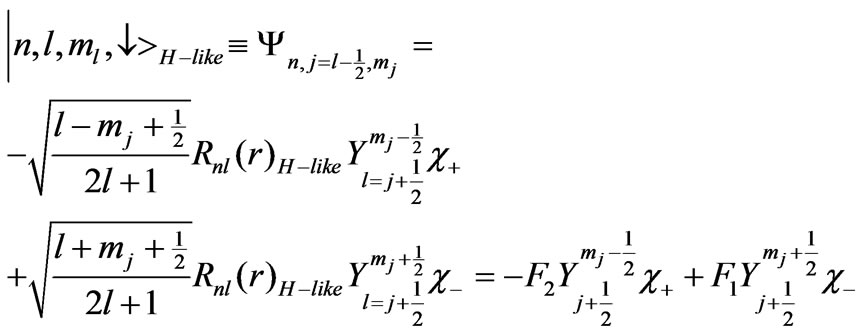(5b)

where

(5c)

Here 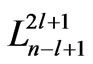are the Laguerre polynomials and 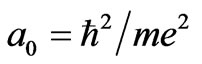is the Bohr radius.

3. Developing Spin Dependent Transition Rates for Photonic Transitions in Dirac Hydrogen-Like Atoms

To develop the spin dependent selection rules for hydrogen-like atoms, we need to consider energy shifts coming from the electric field E and the magnetic field B separately. When the atom is subject to an external electric and magnetic field, it will have interactions through the Hamiltonians: and.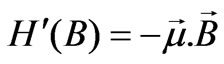

However, the electric and the magnetic field of a photon are not independent fields and they are related to each other with the same vector potential 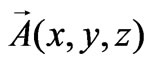which obeys the Coulomb gauge condition (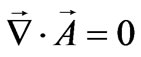). In this case the electric and the magnetic field vectors are given by:

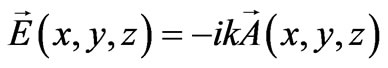(6a)

and

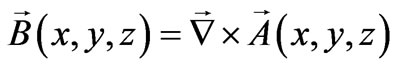(6b)

where 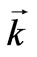is the wave vector of the photon.

In general the effect of the vector potential 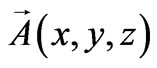on electron is considered through the canonical momentum that produces an interaction potential 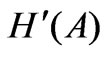which has the linear and the quadratic terms [6]:

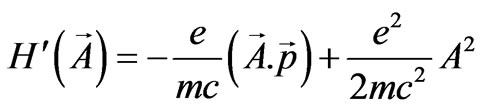(7)

where is the linear momentum of the electron.

We will see that to develop the selection rules for photonic transitions, the Hamiltonian 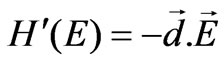will be adequate and the Hamiltonian 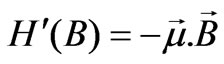will not produce anything new.

Let us first start with the effect of the electric field. In Dirac notations, if at t = 0 the electron is at an initial state

| i > º

given by Equation (5a) and Equation (5b), then at t > 0, because of the interaction with H', there will be a non-zero transition rate to some other states

| f >

which will be called the final states. According to the Golden rule, the transition probability will be proportional to the square of the matrix element of H' between the initial and the final states: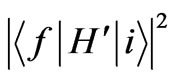. To calculate the matrix element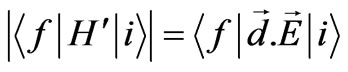, we follow a similar way as followed by Saglam et al. [5]. Namely we will consider two different cases: a) The polarization of the electric field is in x-y plane (along the xor the y-axis) b) The polarization of the electric field is in z-direction. Since the dipole moment vector 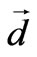is equal to (), for the case a), we calculate the matrix elements of the quantities x ± iy= rsinq exp(±if) and for the case b) we calculate the matrix elements of the quantity: rcos q. For the case a) we can write:

.

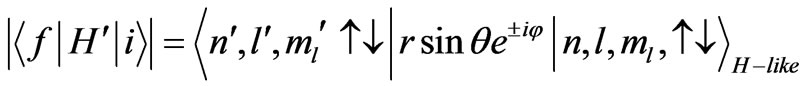
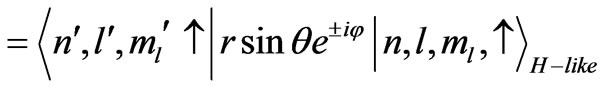
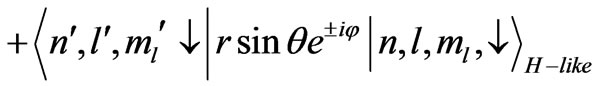
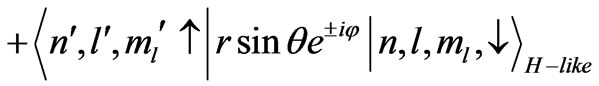
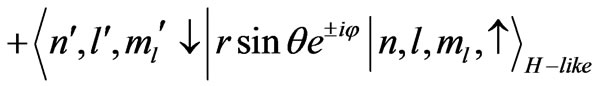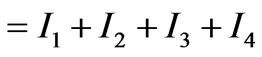(8)

Substitution of Equation (5a) in 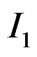we obtain:

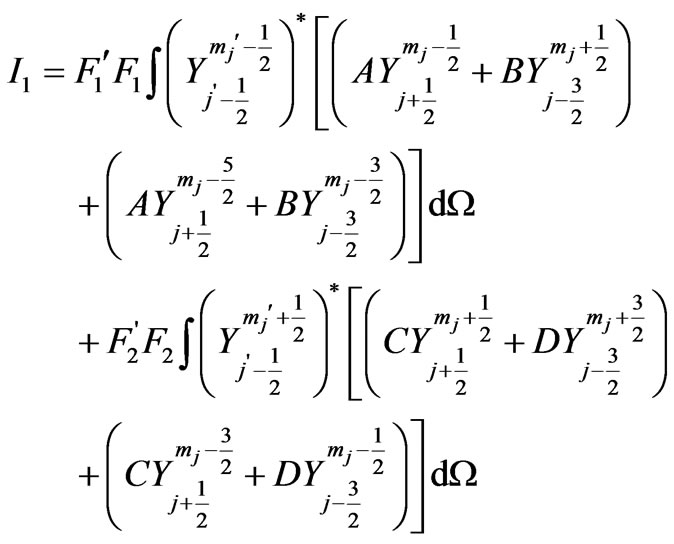(9)

which will be non-zero for:

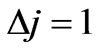; (10a)

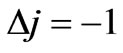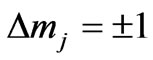; (10b)

To evaluate the integral (9) we have used the relation:

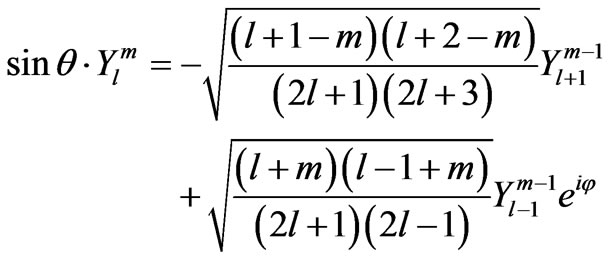(11)

Next substituting Equation (5b) in we obtain:

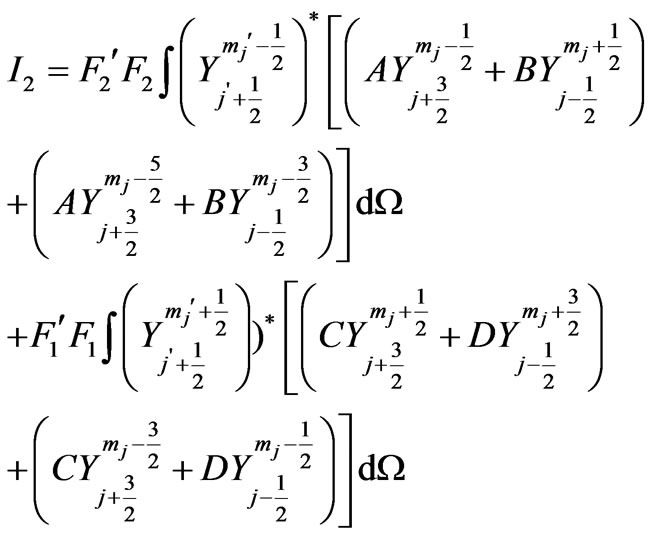(12)

which will be non-zero for:

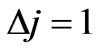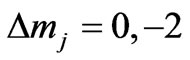; (13a)

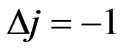; (13b)

where we have used Equation (11) again.

Similarly substitution of Equations (5a) and (5b) in 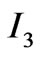we obtain:

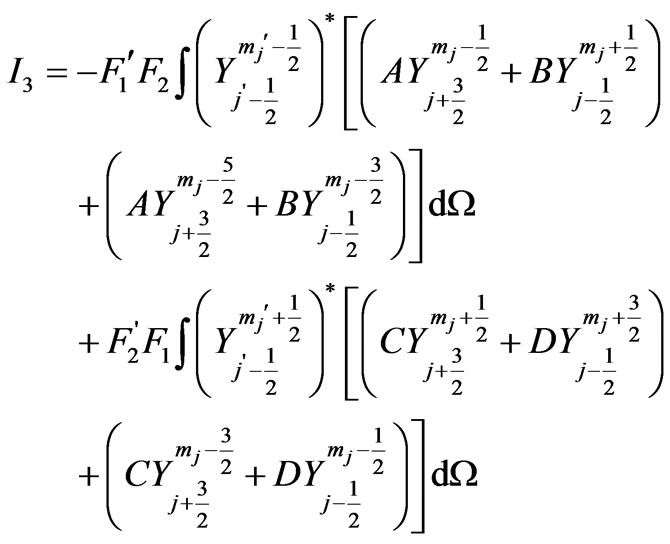(14)

which will be non-zero for

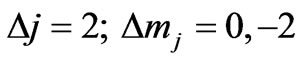(15a)

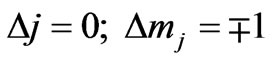(15b)

Similarly substitution of Equations (5a) and (5b) in we obtain:

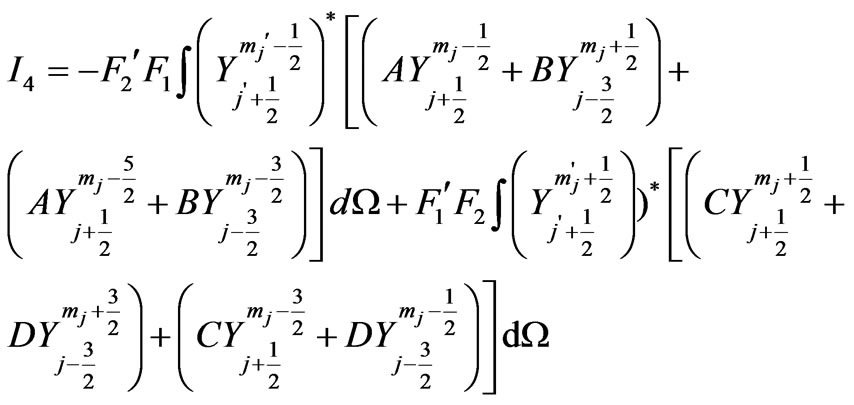(16)

which will be non-zero for

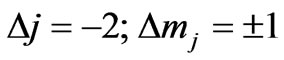
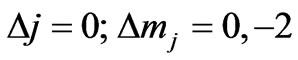(17)

Next we consider the case (b):

+

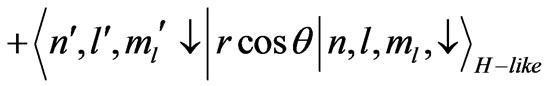
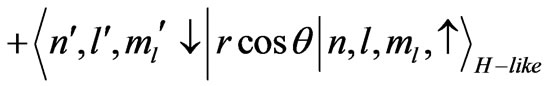
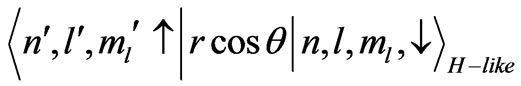
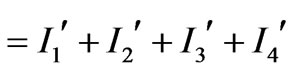(18)

Substitution of Equation (5a) in 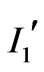we obtain:

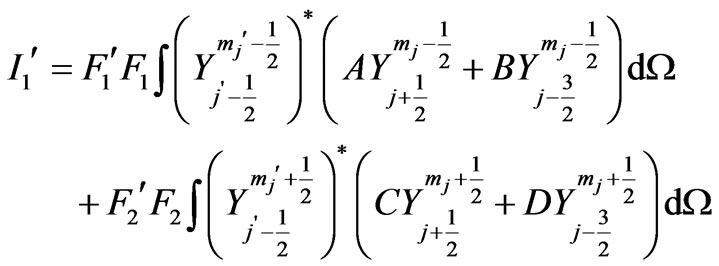(19)

which will be non-zero for

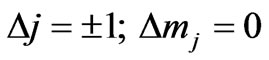(20)

where we used the relations:

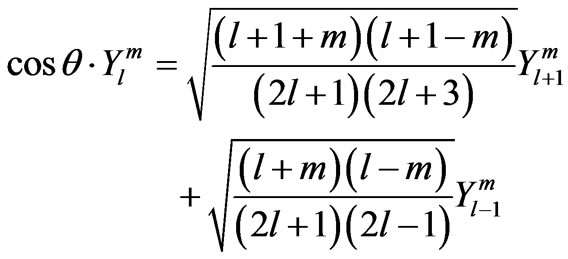(21)

Similarly substitution of Equation (5b) in 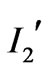we obtain:

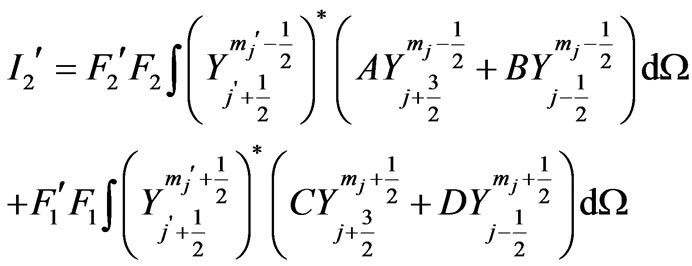(22)

which will be non-zero for

(23)

Substitution of Equations (5a) and (5b) in we obtain:

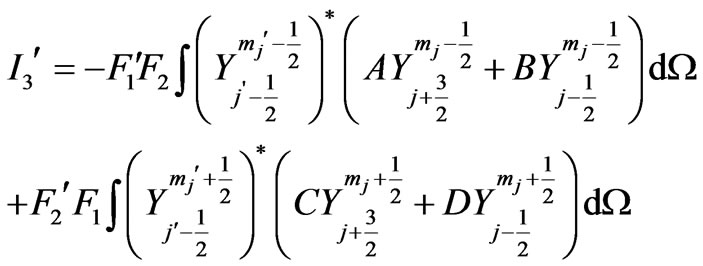(24)

which will be non-zero for

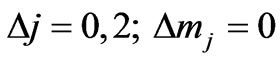(25)

Similarly substitution of Equations (5a) and (5b) in 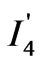we obtain:

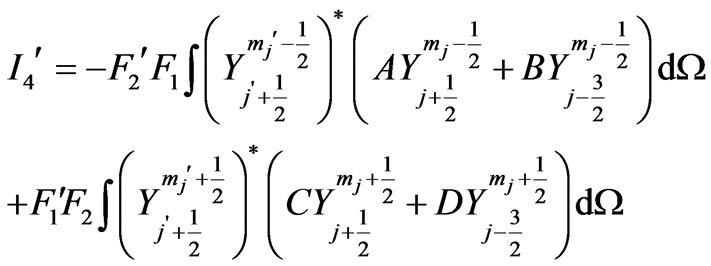(26)

which will be non-zero for 

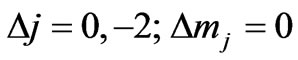. (27)

So far we have considered the effect of the electric dipole transitions. If we want to add the effect of the magnetic field, we must take as the perturbing potential. To calculate the matrix element 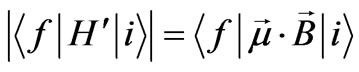 , we will follow a similar way as we did above. Namely we will consider two different cases: a) The polarization of the magnetic field is in x-y plane (along the xor the y-axis) b) The polarization of the magnetic field is in z-direction. The only difference is that the magnetic moment vector 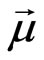will be proportional t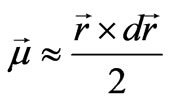o (), so 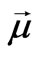will be perpendicular to the vector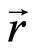. Therefore for the case a) we calculate the matrix elements of the quantity rcos q  and for the case b) we calculate the matrix elements of the quantity x ± iy= rsinq exp(±if ). That means for the case a) we will calculate the matrix elements 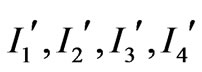given in Equation (18) and for the case b) we will calculate the matrix elements 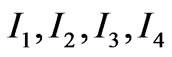given in Equation (8). Therefore the selection rules of the magnetic dipole transitions will be the same as the selection rules for the electric dipole transitions. Combining the results of the Equations (10), (13), (15), (17), (20), (23), (25) and (27), we write the selection rules for a photonic transitions in Hydrogen-like atoms:

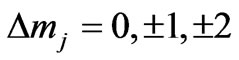
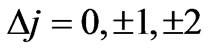(28)

4. Application of the Spin Dependent

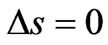Selection Rules to () Transition in Cs According to the conventional selection rules (and) which are derived from the Schrödinger equation in the same way as in Section 3, a transition such as 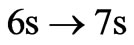is not allowed ( because this is a transition (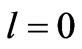) in which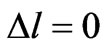, so it does not meet the condition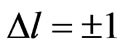). But 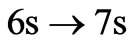transition in Cs atom has been already observed [7-9]. However, the present spin dependent selection rules allow the transition: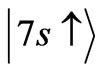 in Cs atom. 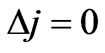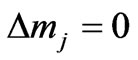Because here we have and which are allowed by the present spin dependent selection rules given in Equation (28). To prove the above transition in detail, let us assume that the outer electron of the Cs atom is initially at the state 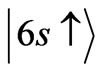=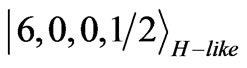. From Equation (5a) we write:

(29)

where A is the normalization constant. When it is excited to the 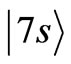state, the possible final states are:

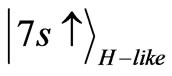and.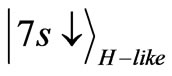

From Equations (5a) and (5b) these states are:

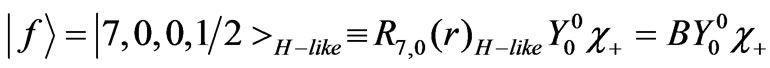(30a)

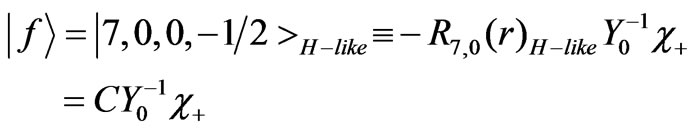(30b)

where B, and C are the normalization constants. Substituting the wave functions from Equation (29) and Equations (30a)-(30b) in Equations (8) and (18) we find:

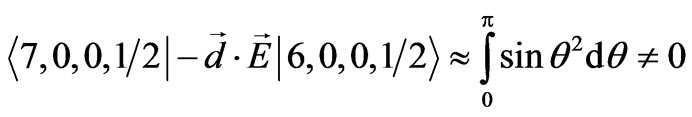(31)

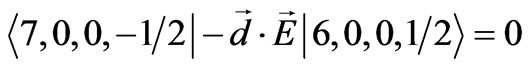(32)

Therefore the non-zero matrix element in Equation (31) gives us a non-transition between the states 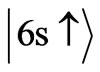and 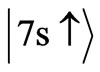which is  also allowed by the present spin dependent selection rules given in Equation (28) (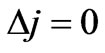and).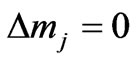

5. Conclusions

We have derived the spin dependent selection rules for photonic transitions in hydrogen-like atoms by using the solution of Dirac equation for hydrogen-like atoms. It is shown that photonic transitions occur when [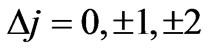while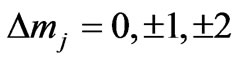]. By applying the present spin dependent selection rules we can explain the observed (6 s7 s) transition in Cesium (Cs) atom [7,8]. Because in the (6s7s) transition in Cesium (Cs) atom we have [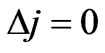while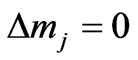] which is an allowed transition according to the present selection rules given in Equation (28). The present result is believed to be helpful for a deeper understanding of the photonic transitions and the spectrum of Cs atom [1]. A detailed study will be presented in the future.

REFERENCES