Journal of Modern Physics
Vol.2 No.1(2011), Article ID:3763,4 pages DOI:10.4236/jmp.2011.21003
On the Hardening of the Spectrum of High-Energy Particles Formed in Heavy-Ion Collisions Considered within the Framework of the Hydrodynamic Approach
1Petersburg State Transport University, St. Petersburg, Russia
2Saint-Petersburg State University, St. Petersburg, Russia
E-mail: dyachenko_a@mail.ru
Received November 23, 2010; revised December 26, 2010; accepted December 26, 2010
Keywords: Hardening of The Spectrum, High-Energy Particles, Heavy-Ion, Hydrodynamics, hot spot, Fermi-Liquid, Freeze-Out Density, Skyrme-Type Interaction, Double Differential Cross-Section, Time Evolution, Evaporation
ABSTRACT
The emission of high-energy particles in 16O + 197Au collisions at energy 20 MeV / nucleon is considered within the framework of the time evolution of a hot spot taking into account the hydrodynamic compression and expansion stages. In addition, the evaporation of the particles that are formed in the early (hot) stage of the evolution of the hot spot is included in the calculation of the spectrum. This leads to a hardening of the particle spectrum in its high-energy part, which is in agreement with experimental data.
1. Introduction
Since the launch of the LHC (Large Hadron Collider) and the work in the RHIC (Relativistic Heavy Ion Collider) there has been a sharply increased interest in the signature of the quark-gluon plasma, which can be successfully described within the framework of relativistic hydrodynamics (to which many papers, including ours, are dedicated [1-3]). This approach has the advantage of describing the yield of secondary particles by a rough description of the dynamics of the heavy-ions collisions and using the macroscopic equations of motion in the calculation of a one-particle distribution function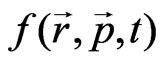 .
.
The same applies to low-energy heavy-ion collisions. The potential of the hot spot model was shown in [4,5], which originates from the work of Bethe in 1938 [6], for describing the non-equilibrium components of the spectrum of emitted particles. In [5], the evolution of a hot spot is considered within the framework of the hydrodynamic approach, including a stage of compression, expansion, and spreading when the critical density of the expanding nuclear system is attained. The spectrum of emitted particles was calculated by the distribution function 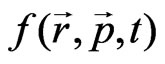
 in the final stage of evolution of the system. In the present work, we take into consideration the emission of particles at early stages of the evolution of a hot spot. This leads to the hardening of the spectrum of protons, which is in accordance with experimental data.
in the final stage of evolution of the system. In the present work, we take into consideration the emission of particles at early stages of the evolution of a hot spot. This leads to the hardening of the spectrum of protons, which is in accordance with experimental data.
2. Model for Calculation
The equation of state of an excited nuclear system depends on the degree of equilibrium in the system. Considering the nuclear system within the Fermi-liquid theory, Bertsch [7] found the relaxation time  to the state of local thermodynamic equilibrium.
to the state of local thermodynamic equilibrium.
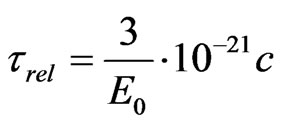 (1)
(1)
where 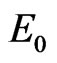 is the initial collision energy in MeV per nucleon. Comparing
is the initial collision energy in MeV per nucleon. Comparing 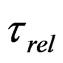 and
and the characteristic time of the collision process,
the characteristic time of the collision process,  , given by
, given by  (where
(where  is the characteristic longitudinal dimension of the resulting system and
is the characteristic longitudinal dimension of the resulting system and 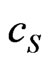 is the velocity of sound in nuclear matter), we can conclude that, for energies 10-20 MeV per nucleon,
is the velocity of sound in nuclear matter), we can conclude that, for energies 10-20 MeV per nucleon, 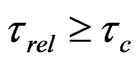 and the most appropriate equation of state is the equation of state with an anisotropic pressure tensor. With increasing collision energy, these estimates show that
and the most appropriate equation of state is the equation of state with an anisotropic pressure tensor. With increasing collision energy, these estimates show that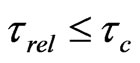
 , allowing local thermodynamic equilibrium and the applicability of hydrodynamics with an isotropic pressure tensor. The calculation of the hydrodynamic evolution of a hot spot that is formed in heavy-ion collisions is described in [5].
, allowing local thermodynamic equilibrium and the applicability of hydrodynamics with an isotropic pressure tensor. The calculation of the hydrodynamic evolution of a hot spot that is formed in heavy-ion collisions is described in [5].
The equation of state determining the dependence of the pressure 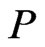 and energy density
and energy density 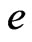 on the density
on the density 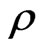 is a sum of kinetic terms and interaction terms,
is a sum of kinetic terms and interaction terms, 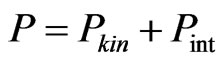 and
and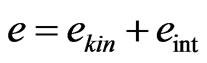 . The contribution of the interaction terms (we chose the Skyrme-type interaction) to the pressure and energy density are
. The contribution of the interaction terms (we chose the Skyrme-type interaction) to the pressure and energy density are
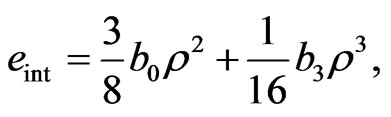
 (2)
(2)
where 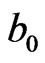 and
and 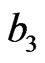 are effective interaction parameters. We assume that nucleons move in a self-consistent potential
are effective interaction parameters. We assume that nucleons move in a self-consistent potential
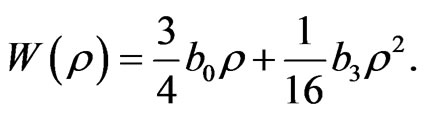 (3)
(3)
The form of the kinetic terms depends on the relaxation rate of the excited nuclear system. The longitudinal component of the anisotropic pressure tensor can be written as follows:
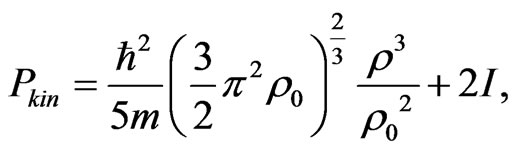
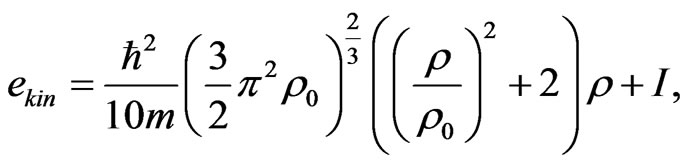 (4)
(4)
where 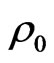 is the equilibrium density,
is the equilibrium density,  is the nucleon mass,
is the nucleon mass, 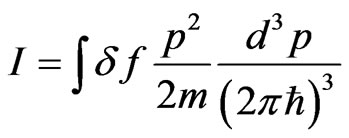 is the effective thermal energy density. For the isotropic pressure
is the effective thermal energy density. For the isotropic pressure
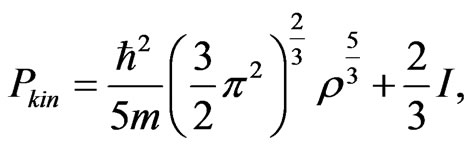
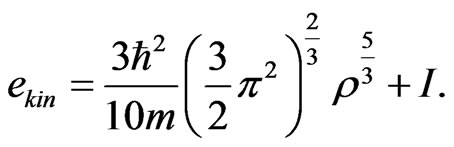 (5)
(5)
After the stages of compression and expansion, the nuclear system reaches a critical density,
 , determined only by the parameters of effective interaction from the
, determined only by the parameters of effective interaction from the
condition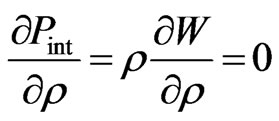 . In this condition,
. In this condition, 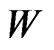 is
is the self-consistent potential and
the self-consistent potential and 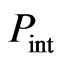 is the pressure term determined by the effective interaction. Therefore,
is the pressure term determined by the effective interaction. Therefore, 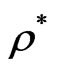
is given by
 .
.
The double differential cross-section of the formation of secondary particles (protons) is given by
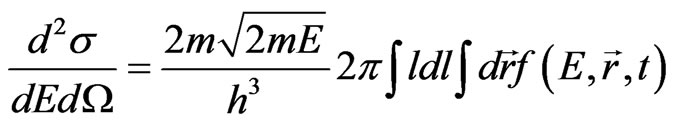 (6)
(6)
where  is the impact parameter, and the distribution function
is the impact parameter, and the distribution function 
 for nucleons, taking into account the motion of the medium, has the Fermi form
for nucleons, taking into account the motion of the medium, has the Fermi form
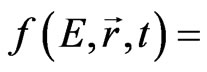
 . (7)
. (7)
Here, 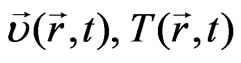 are, respectively, the velocity and temperature fields, obtained from the solutions of the hydrodynamic equations in a system of colliding nuclei with equal velocities,
are, respectively, the velocity and temperature fields, obtained from the solutions of the hydrodynamic equations in a system of colliding nuclei with equal velocities, 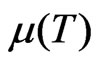 is the chemical potential,
is the chemical potential, 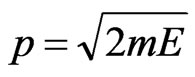 is
is the momentum, and
the momentum, and 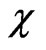 is
is the energy shift arising from including a surface term in the nucleon binding energy. The distribution function (7) in expression (6) was determined at time
the energy shift arising from including a surface term in the nucleon binding energy. The distribution function (7) in expression (6) was determined at time
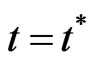 , corresponding to the achievement of the critical density
, corresponding to the achievement of the critical density 
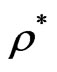 of the system. The evaporation of particles at early times
of the system. The evaporation of particles at early times 

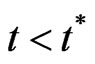 gives an additional contribution to the cross section (6)
gives an additional contribution to the cross section (6)
 . (8)
. (8)
Here, expression (7) can be used for 
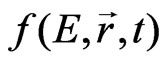 if we take into account the fact that the emitted nucleons have to overcome the attraction of the self-consistent nuclear potential. Expression (8) is obtained from the equation for the total derivative of the distribution function
if we take into account the fact that the emitted nucleons have to overcome the attraction of the self-consistent nuclear potential. Expression (8) is obtained from the equation for the total derivative of the distribution function 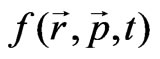

 ,. (9)
,. (9)
where
 ,
, 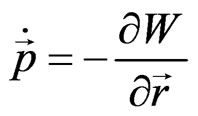 , after the transformation of the volume integral to a surface integral over the surface
, after the transformation of the volume integral to a surface integral over the surface 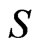 of the forming hot spot
of the forming hot spot :
:
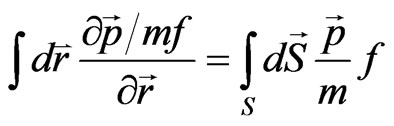 .
.
In the relaxation approximation given in [7]
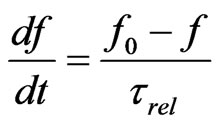 where
where  is
is the equilibrium distribution function. The equilibrium distribution function (7) is included in expression (8), since the relaxation factor
the equilibrium distribution function. The equilibrium distribution function (7) is included in expression (8), since the relaxation factor
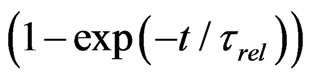 determining the degree of equilibrium of the system is close to 1 for collision times
determining the degree of equilibrium of the system is close to 1 for collision times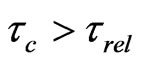
 . The first term in (9) leads to expression (6) after integration over time from t = 0, when there is no emission of nucleons, to
. The first term in (9) leads to expression (6) after integration over time from t = 0, when there is no emission of nucleons, to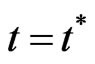 , when the system reaches the critical density
, when the system reaches the critical density .
. The last term in (9) can be neglected, since
The last term in (9) can be neglected, since 
 if a Gaussian surface passing through the border of the nucleus is chosen. Expression (8) for the double differential cross section is similar to the formula used in [8]. The contribution to the differential cross section determined by expression (8) is essential in the tails of the energy spectrum, as it is determined by the temperature at the early stages of the evolution of a system of higher temperature.
if a Gaussian surface passing through the border of the nucleus is chosen. Expression (8) for the double differential cross section is similar to the formula used in [8]. The contribution to the differential cross section determined by expression (8) is essential in the tails of the energy spectrum, as it is determined by the temperature at the early stages of the evolution of a system of higher temperature.
3. Results and Discussions
The calculation of proton production cross sections was carried out according with Skyrme’s interaction parameters equal to 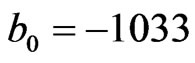 MeV fm3,
MeV fm3, 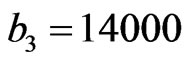 MeV fm6. The chosen parametrization of effective forces corresponds to realistic values of compression module
MeV fm6. The chosen parametrization of effective forces corresponds to realistic values of compression module  MeV and the normal density
MeV and the normal density 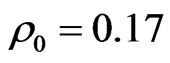 fm-3. The calculated mean temperature
fm-3. The calculated mean temperature 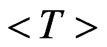 of the area of the critical density
of the area of the critical density 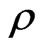 * from which the secondary particles are emitted was analysed in dependence on the value of critical density and on the bombarding energy [9]. The calculations of the mean temperature coincide with the result of [10] and correspond to the weak dependence on the
* from which the secondary particles are emitted was analysed in dependence on the value of critical density and on the bombarding energy [9]. The calculations of the mean temperature coincide with the result of [10] and correspond to the weak dependence on the 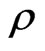 * value.
* value.
The comparison of the double differential cross sections of emission of protons, determined by the sum of expressions (6) and (8) for the reaction 16O + 197Au at 315 MeV, improves the agreement between calculated and experimental data (spectra of protons emitted at angles of 20, 40, 60, and 80º [11]).
In Figure 1, the spectrum calculated using formula (6) is compared with experimental data from [11]. In Figure 2, the spectrum calculated as the sum of the components determined by (6) and (8) is compared with the same experimental data from [11].
The critical density 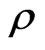 *, or, in other words, the freeze-out density is a free parameter of the model in some studies, using the hydrodynamic approach. This allows to increase freeze-out temperature on 30% by increase the critical density on 20%. This can be seen from Fig. 1, where
*, or, in other words, the freeze-out density is a free parameter of the model in some studies, using the hydrodynamic approach. This allows to increase freeze-out temperature on 30% by increase the critical density on 20%. This can be seen from Fig. 1, where  6.3 MeV and from Figure 2, where
6.3 MeV and from Figure 2, where 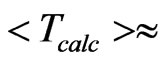 8 MeV. In the present approach,
8 MeV. In the present approach, 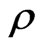 * is not a free parameter and defined by the parameters of effective interaction
* is not a free parameter and defined by the parameters of effective interaction  and
and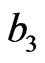 . Inclusion of the particle evaporation at the early stage of hydrodynamic approach allows to obtain the agreement between the
. Inclusion of the particle evaporation at the early stage of hydrodynamic approach allows to obtain the agreement between the
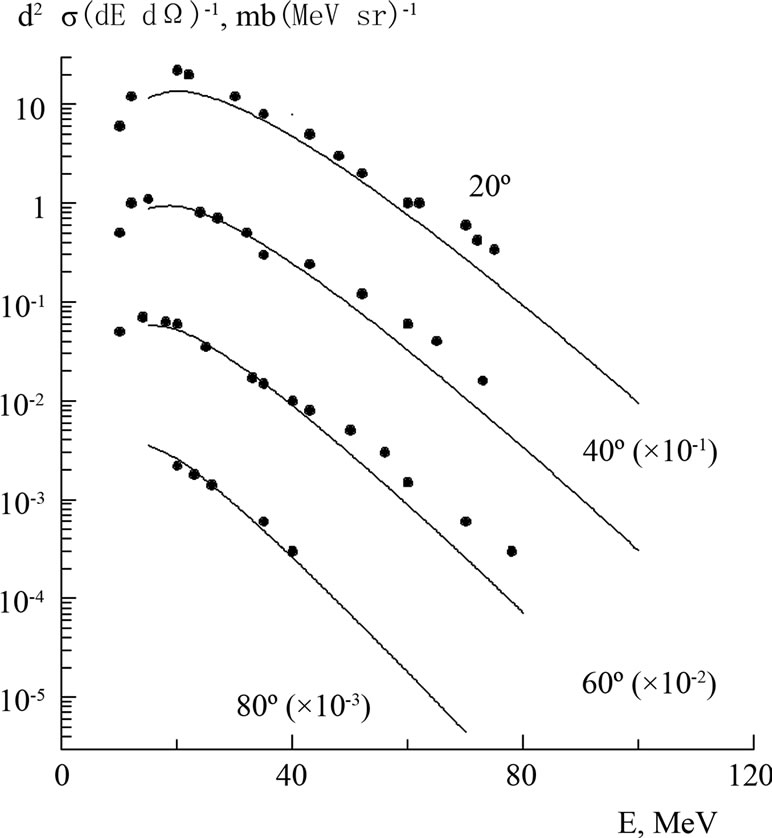
Figure 1. Comparison of the double differential cross sections of protons emitted in the 16O + 197Au reaction (315 MeV) at angles of 20, 40, 60, and 80º calculated according to expression (6) (solid lines) with the experimental data from [11] (circles).
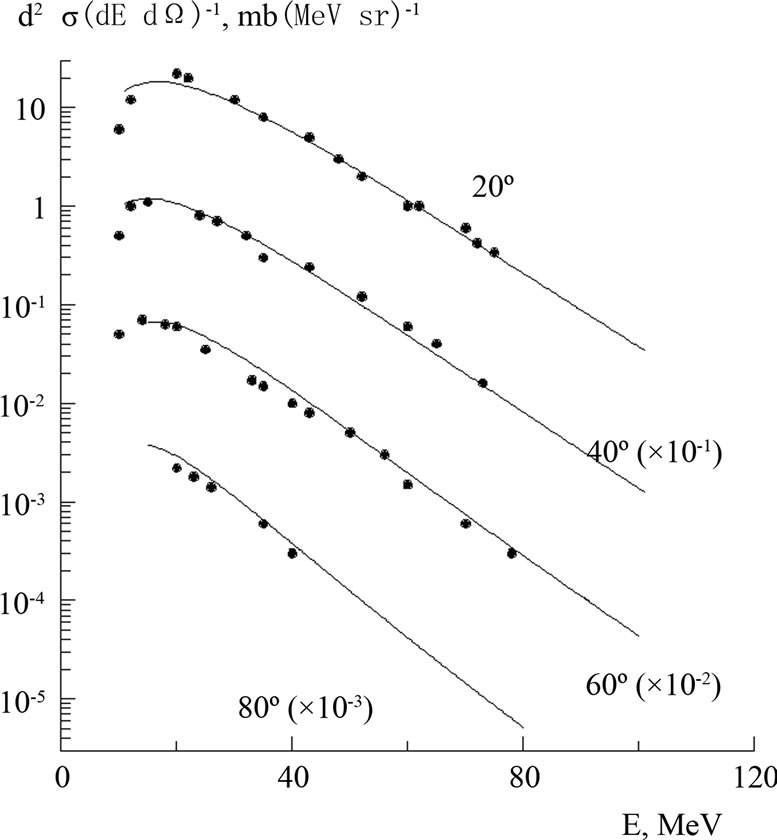
Figure 2. Comparison of the double differential cross sections of protons emitted in the 16O +197 Au reaction (315 MeV) at angles of 20, 40, 60, and 80º determined by the sum of expressions given by equations (6) and (8) (solid lines) with the experimental data from [11] (circles).
experimental data and theoretical calculation in the absence of free parameters.
4. Conclusion
Thus, the emission of high-energy particles in 16O + 197Au collisions at energy 315 MeV was considered within the framework of the time evolution of a hot spot taking into account the hydrodynamic compression and expansion stages. It can be seen that taking into consideration the evaporation of particles in the early stage of the evolution of a hot spot leads to a hardening of the spectrum of the emitted secondary particles and improves the agreement with the experimental data. It is important that all characteristics of the secondary particles spectra are calculated unambiguously in this model. The same approach can be used to relativistic energies.
REFERENCES
- H. Petersen, J. Steinheimer, G. Burau, M. Bleicher and H. Stöсker, “Fully Integrated Transport Approach to Heavy ion Reactions with Hydrodynamic Stage,” Physical Review, vol. C78, no. 4, 2008, p. 044901.
- A. T. D’yachenko and O. V. Lozhkin, “Possible Evidence of Non-hadronic Degrees of Freedom in the Spectra of Kaons Produced in Relativistic Nucleus-Nucleus Collisions, ” Bulletin of the Russian Academy of Sciences: Physics, vol. 70, no. 5, 2006, pp. 711-714.
- A. T. D’yachenko and O. V. Lozhkin, “Kaon and Pion Spectra in Relativistic and Ultrarelativistic Nucleus-Nucleus Collisions,” Bulletin of the Russian Academy of Sciences: Physics, vol. 71, no. 6, June 2007, pp. 880-883. doi:10.3103/S1062873807060251
- O. V. Bochkarev and A. A. Korsheninnikov, “Nonequilibrium Processes in the Emission of Neutrons from the Reactions with Ions of Helium, lithium-6 and Carbon. Analysis of Experimental Data,” Preprint of I. V. Kurchatov Institute of Atomic Energy, Moscow, 1983.
- A. T. D’yachenko, “The Fast Particles Spectrum in Fluid Dynamic Model of Heavy Ion Collisions,” Physics of Atomic Nuclei, vol. 57, no. 11, November 1994, pp. 1930-1936.
- H. A. Bethe, “Possible Deviation from the Evaporation Model of Nuclear Reaction,” Physical Review, vol. 53, no. 8, April 1938, p. 675.
- G. Bertsch, “The Collision Integral in Nuclear Matter at Zero Temperature,” Zeitschrift für Physik, vol. A289, no. 1, December 1978, pp. 103-105.
- J. P. Bondorf , J. N. De, J. Fai, A. O. T. Karvinen, B. Jakobsson and J. Randrup, “Promptly Emitted Particles in Nuclear Collisions,” Nuclear Physics, vol. A333, no. 2, January 1980, pp. 285-301.
- A.T. D’yachenko, “Subthreshold K meson and Antiproton Production in the Nucleus-Nucleus Collisions within the Framework of the Fluid Dynamics Approach,” Journal of Physics G: Nuclear and Particle Physics, vol. 26, no. 6, June 2000, pp. 861-869. doi:10.1088/0954-3899/26/6/309
- H. Stöcker and W. Greiner, “High Energy Heavy Ion Collisions-Probing the Equation of State of Highly Excited Hadronic Matter,” Physics Reports, vol. 137, no. 5, May 1986, pp. 277-392. doi:10.1016/0370-1573(86)90131-6
- T. J. M. Symons, P. Doll, M. Bini, D. L. Hendrie, J. Mahoney, G. Mantzouranis, D. K. Scott, K. Van Bibber, Y. P. Viyogi, H. H. Wieman and C. K. Gelbke, “High Energy Proton Emission in Reaction Induced by 315 MeV 16O ions,” Physics Letters, vol. B94, no. 2, July 1980, pp. 131-134.

