Applied Mathematics
Vol.09 No.05(2018), Article ID:84855,16 pages
10.4236/am.2018.95036
Global Dynamic Analysis of a Vector-Borne Plant Disease Model with Discontinuous Treatment
Hengmin Lv1*, Lizhi Fei1,2, Zhen Yuan1, Fumin Zhang3
1Department of Basic Course Education, Ji’an College, Ji’an, China
2College of Mathematics, Sichuan University, Chengdu, China
3Key Laboratory of Jiangxi Province for Numerical Simulation and Emulation Techniques, Gannan Normal University, Ganzhou, China
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 2, 2018; Accepted: May 25, 2018; Published: May 28, 2018
ABSTRACT
This paper proposes a vector-borne plant disease model with discontinuous treatment strategies. Constructing Lyapunov function and applying non-smooth theory to analyze discontinuous differential equations, the basic reproductive number is proved, which determines whether the plant disease will be extinct or not. If , the existence and global stability of disease-free equilibrium is established; If , there exists a unique endemic equilibrium which is globally stable. The numerical simulations are provided to verify our theoretical results, which indicate that after infective individuals reach some level, strengthening treatment measures is proved to be beneficial in controlling disease transmission.
Keywords:
Vector-Borne, Plant Disease Model, Basic Reproduction Number, Discontinuous Treatment

1. Introduction
The plants play an important role in our lives, as most of our daily food, clothing and building materials come from plants. With the change of environment, there are outbreaks of plant diseases, which seriously affect the health of plants and people’s life, such as huanglongbing [1] , Blackleg [2] . We know that plant diseases have been responsible for the death and suffering of millions of people and countless animals [3] . Controlling the outbreak and spread of plant diseases has become the common goal of scientists. Available control measures include biological, cultural, and chemical methods [4] . Chemical control is a quite effective method, but the residues of chemical drugs have a direct negative impact on environment and thus are not encouraged. To effectively control plant disease and to reduce the harm to environment, it is crucial to understand disease transmission dynamics.
The prevention and control of plant infectious diseases is of vital importance in agricultural production [5] . To work with the plant disease, we first understand how they spread. There are many ways that plant viruses interact with the vectors; this transmission works in the following way. The vectors consume sap from an infected host through their stylet. When the infected vector contacts a healthy plant, some virus particles leave the vector and invade the plant [6] . So the vector-borne is a very important part of the transmission of plant diseases.
Treatment plays a very important role to control the spread of diseases. In recent years, many researchers [7] [8] [9] [10] have studied some mathematical models incorporating treatment. For example, in [11] , Wang and Ruan studied an epidemic model, and provide the limited resources for the treatment of patients. In [12] , Wang proposed constant treatment, which simulates a limited capacity for treatment. In practice, when the number of infectives is large, the constant treatment is suitable for hypothesis of model. Recently, discontinuous treatment strategies are proposed by [13] [14] . The results show that discontinuous treatment strategies would be accord with real condition. Applying this discontinuous treatment strategy makes the mathematical model a discontinuous system. At the same time, some non-smooth analysis techniques [15] are used for this system.
In [16] , Shi and Zhao presented a vector-borne plant disease model, but they do not studied treatment to the infected plant host. Treating infected plant is a quite effective method which to control the outbreak of the plant disease. Although continuous treatment is an effective method, the outbreak of the plant disease is periodic, and continuing treatment can be a huge waste of resources. In order to be realistic, we built a vector-borne plant disease model with discontinuous treatment.
The paper is organized as follows. In the next section, we will construct the model and introduce the rational assumptions for model. In Section 3, positivity of the solution for the model will be clearly discussed. We obtain the existence of possible equilibria, the basic reproductive number, and the stability of equilibria in Section 4. In Section 5 and Section 6, we summarize our main results and main results are numerically simulated.
2. Model and Preliminaries
To construct the model, the following assumptions are being made by Shi et al. in [16] .
(A1) The total of the insect vector population is divided into X and Y, which denotes the densities of the susceptible vector and infective vector at time t, respectively. The total of the plant host population is divided into S, I, and R, which represents the numbers of the susceptible, infective, and recovered host plant population at time t, respectively. At the same time, we assume that the number of plants in one area is fixed. The total number of plants is a positive constant. In fact, when a plant has died, it would be replaced by a new plant to keep the total number of plants. Further, we assume that those new plants are susceptible, i.e., we chose the birth rate of susceptible plant host as .
(A2) The susceptible plants can be infected not only by the infected insect vectors but also by the infected plants.
(A3) A susceptible vector can be infected only by an infected plant host, and after it is infected, it will hold the virus for the rest of its life. Further, there is no vertical infection being considered.
(A4) The replenishment rate of insect vectors is a positive constant, and all of the new born vectors are susceptible.
According to the principle of the compartmental model, consider the following model with discontinuous treatment:
(2.1)
Here the dimensionless variables and parameters (with parameter values) are given in Table 1.
The function represents the treatment rate. satisfies the following assumptions. Obviously, the treatment rate should be nondecreasing as the number of infectious individuals is increasing. The following assumption will be needed throughout the paper.
(H1) is nondecreasing and has at most a finite number of jump discontinuities in every compact interval. No loss of generality, we always assume that is continuous at , otherwise we define to be . Here denotes the right limit of as .
By adding the fourth and fifth equations of system (2.1), we get
(2.2)
where . From Equation (2.2), we easily get as
Note that . Since the variable R and X does not appear in the first two equations of model (2.1), meanwhile, let’s substitute X for in
the fifth equation. We only need to study the first two equations and the fifth
Table 1. Dimensionless variables and parameters (with illustrative parameter values) in system (2.1).
equation of model (2.1), thereby lowering the order of the system to be studied, i.e.
(2.3)
where . Obviously,
(2.4)
is the positively invariant set for system (2.3).
According to the definition of solutions for differential equations with discontinuous right-hand sides in [15] [17] , is called a solution with initial condition
(2.5)
of model (2.3) on , if it is absolutely continuous on any compact subinterval of , and almost everywhere on (abbreviated to a.e. on ) satisfies the following differential inclusion:
(2.6)
where . Here, and denote the left limit and the right limit of the function at I, respectively.
From (H1), it is clear that the set map
(2.7)
is an upper semi-continuous set-valued map with non-empty compact convex values. By the measurable selection theorem [15] , if is a solution of model (2.3) on , then there is a measurable function such that
(2.8)
3. Positivity
In this section, we will prove the positive of the solution to the initial condition of the model (2.3) with positive initial value. First, we will prove the following theorem.
Theorem 3.1. Suppose that assumption (H1) holds and let be the solution with initial condition (2.5) of model (2.3) on . Then is nonnegative on .
Proof: By the definition of a solution of (2.3) in the sense of Filippov, must be a solution to differential inclusion (2.6). From the first equation of (2.6), we have
(3.1)
for all .
Based on the previous hypothesis of (H1), we have and is continuous at . Combining the continuity of at , it may be concluded that there exists a positive constant such that is continuous as . On this account, when the differential inclusion (2.6) becomes the following system of differential equations:
(3.2)
We divide this into four cases to discuss the positivity of the solutions for (2.6).
1) .
From (3.2), we see that for all .
2) .
By the continuity of at and , we conclude and for all . If it is not true, then we can set
(3.3)
If , then from for , we have . This is a contradiction.
If , then there is a such that and on . Therefore, the second equation of (3.2) implies
(3.4)
We have
(3.5)
This is also a contradiction. Hence, and are positive for all . The same conclusion can be reached for the following two cases.
3) .
4) . This completes the proof.
4. The Equilibria and Their Stability
In this section, we will discuss the existence of equilibria of system (2.3). First, we prove the existence of endemic equilibrium.
Let is a constant solution of (2.3), where satisfies the following system:
(4.1)
Since , there always exists a disease-free equilibrium of the model (2.3), where . Next, we consider that the existence of an endemic equilibrium of the model (2.3).
It follows from the first and third equations of (4.1), we conclude that
(4.2)
Substituting (4.2) into the second inclusion of (4.1), we have the follows
(4.3)
where
Denote
(4.4)
and let
(4.5)
We next claim that is the basic reproductive number for the model (2.3) which will determine the existence of an endemic equilibrium.
Theorem 4.1. Suppose that assumption (H1) holds. If , then there only exists a disease-free equilibrium . If , then there exists a unique positive endemic equilibrium except .
Proof: By , we get . Since is nonincreasing on I and is nondecreasing on I. For this reason, the inclusion (4.3) is only valid at . Hence, the model (2.3) has a unique disease-free equilibrium as long as .
From (4.4), we have the following
(4.6)
where
If , then , and the Equation (4.6) has a unique positive root I, where
(4.7)
If
, then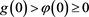 . Meanwhile, the inequality
. Meanwhile, the inequality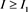 , it implies
, it implies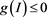 . Therefore, the set
. Therefore, the set
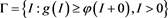 (4.8)
(4.8)
is bounded and non-empty. We can write

It follows easily that
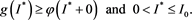 (4.9)
(4.9)
We claim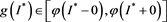 . Assumption, contrary to our claim, that
. Assumption, contrary to our claim, that
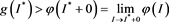
From (H1), there exists a 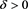 such that
such that
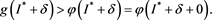 (4.10)
(4.10)
This contradicts the definition of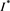 . Thus, we have
. Thus, we have 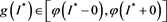 . That is to say,
. That is to say, 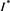 is a positive solution of the inclusion (4.3). We proceed to show that
is a positive solution of the inclusion (4.3). We proceed to show that 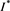 is the only one positive solution of the inclusion (4.3). If the inclusion (4.3) has another positive solution
is the only one positive solution of the inclusion (4.3). If the inclusion (4.3) has another positive solution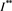 , then there must exist two numbers
, then there must exist two numbers
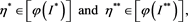 (4.11)
(4.11)
which satisfy
 (4.12)
(4.12)
and

Subtracting (4.13) from (4.12) gives

which implies

This is a contradiction. Hence, 

Next, we prove the global stability of the disease-free equilibrium and the endemic equilibrium. We do this in several steps. We first investigate the local properties of the equilibria of system (2.3).
Theorem 4.2. Assume (H1) holds. The disease-free equilibrium 


Proof: We analyze the stability of the disease-free equilibrium by investigating the eigenvalues of the Jacobian matrix of model (2.3) at

Thus, the characteristic equation at the disease-free equilibrium 

It is easy to see that one of the roots with respect to 



From (4.18) and Routh-Hurwitz criteria [18] , it is easily seen that both the real parts of 







We have shown that there exists a positive endemic equilibrium if and only if 
Theorem 4.3. Suppose that assumption (H1) holds. If

Proof: The Jacobian matrix of (2.3) at the endemic equilibrium 

Replacing




The characteristic equation of 

where
Since 


Then
Hence, all of the Routh-Hurwitz criteria are satisfied. Thus it follows that the endemic equilibrium 

Next, we will prove global stability of the disease-free equilibrium and endemic equilibrium of (2.3). We need to use the LaSalle-type invariance principle for the differential inclusion (Theorem 3 in [19] ) to prove their global stability.
Let

Set

and
For any


Hence,

When


It shows that 
Furthermore, when

When




Hence, the largest weakly invariant subset of 

When

From the first equation of (4.23) and x = 0, it may be concluded that




Next, we demonstrate the global stability of the endemic equilibrium 
Theorem 4.4. Suppose that assumption (H1) holds. If

Proof: Let

Write
and

For any


Hence

The monotonicity of 



If




Therefore, 

5. Numerical Simulation
To make our analysis more intuitive, some numerical simulations of solutions of the model (2.6) is provided which to illustrate the influence of insect vector and discontinuous treatment on the spread of plant disease. We apparent a treatment function satisfying (H1) as follows:

where


To better illustrate the effects of non-continuous healing on the spread of plant disease, the following parameters are derived from [16] . Let












If we fixed all parameter values as follows:












Figure 1. Stability of disease-free equilibrium. The parameters are fixed as follows:












6. Discussion
As for the plant infectious disease model, our main object is to investigate the effect of the insect vector and discontinuous treatment function on the dynamics of spreading the plant disease. We calculated the basic reproduction number


In this paper, we studied the existence, local stability and global stability of the disease-free equilibrium and endemic equilibrium of the system (2.3) in detail. By building a suitable Lyapunov function, and the Jacobian matrix method,
Figure 2. Stability of endemic equilibrium. The parameters are fixed as follows:








employing Routh-Hurwitz criteria and LaSalle-type invariance principle, the main results as shown in Theorems 4.2, 4.3 and 4.4 have been derived. Our main results indicate that if


Acknowledgements
The research have been supported by The Natural Science Foundation of China (11561004), the Science and Technology research project of Jiangxi Provincial Education Department (171373, 171374, GJJ170815), The bidding project of Gannan Normal University (16zb02).
Cite this paper
Lv, H.M., Fei, L.Z., Yuan, Z. and Zhang, F.M. (2018) Global Dynamic Analysis of a Vector-Borne Plant Disease Model with Discontinuous Treatment. Applied Mathematics, 9, 496-511. https://doi.org/10.4236/am.2018.95036
References
- 1. Lee, J.A., Halbert, S.E., Dawson, W.O., et al. (2015) Asymptomatic Spread of Huanglongbing and Implications for Disease Control. Proceedings of the National Academy of Sciences, 112, 7605-7610. https://doi.org/10.1073/pnas.1508253112
- 2. Smith, A.B., Beeck, C.P., Cowling, W.A., et al. (2013) A Bivariate Mixed Model Approach for the Analysis of Plant Survival Data. Euphytica, 190, 371-383. https://doi.org/10.1007/s10681-012-0791-0
- 3. Xia, L., Gao, S., Zou, Q., et al. (2013) Analysis of a Nonautonomous Plant Disease Model with Latent Period. Applied Mathematics and Computation, 223, 147-159. https://doi.org/10.1016/j.amc.2013.08.011
- 4. Wang, J., Zhang, F., Wang, L., et al. (2016) Equilibrium, Pseudoequilibrium and Sliding-Mode Heteroclinic Orbit in a Filippov-Type Plant Disease Model. Nonlinear Analysis: Real World Applications, 31, 308-324. https://doi.org/10.1016/j.nonrwa.2016.01.017
- 5. Zhao, W., Li, J., Zhang, T., et al. (2017) Persistence and Ergodicity of Plant Disease Model with Markov Conversion and Impulsive Toxicant Input. Communications in Nonlinear Science and Numerical Simulation, 48, 70-84. https://doi.org/10.1016/j.cnsns.2016.12.020
- 6. Jackson, M. and Chen-Charpentier, B.M. (2016) Modeling Plant Virus Propagation with Delays. Journal of Computational and Applied Mathematics, 2016, 1-14.
- 7. Xue, Y. and Wang, J. (2012) Backward Bifurcation of an Epidemic Model with Infectious Force in Infected and Immune Period and Treatment. Abstract and Applied Analysis, 2012, Article ID: 647853. https://doi.org/10.1155/2012/647853
- 8. Hussaini, N. and Winter, M. (2010) Travelling Waves for an Epidemic Model with Non-Smooth Treatment Rates. Journal of Statistical Mechanics, 11, Article ID: 11019. https://doi.org/10.1088/1742-5468/2010/11/P11019
- 9. Brauer, F. (2008) Epidemic Models with Heterogeneous Mixing and Treatment. Bulletin of Mathematical Biology, 70, 1869-1885. https://doi.org/10.1007/s11538-008-9326-1
- 10. Hu, Z., Liu, S. and Wang, H. (2008) Backward Bifurcation of an Epidemic Model with Standard Incidence Rate and Treatment Rate. Nonlinear Analysis: Real World Applications, 9, 2302-2312. https://doi.org/10.1016/j.nonrwa.2007.08.009
- 11. Wang, W. and Ruan, S. (2004) Bifurcations in an Epidemic Model with Constant Removal Rate of the Infectives. Journal of Mathematical Analysis and Applications, 291, 775-793. https://doi.org/10.1016/j.jmaa.2003.11.043
- 12. Wang, W. (2006) Backward Bifurcation of an Epidemic Model with Treatment. Mathematical Biosciences, 201, 58-71. https://doi.org/10.1016/j.mbs.2005.12.022
- 13. Guo, Z. Huang, L. and Zou, X. (2012) Impact of Discontinuous Treatments on Disease Dynamics in an SIR Epidemic Model. Mathematical Biosciences and Engineering, 9, 97-110. https://doi.org/10.3934/mbe.2012.9.97
- 14. Zhang, T., Kang, R., Wang, K. and Liu, J. (2015) Global Dynamics of an SEIR Epidemic Model with Discontinuous Treatment. Advances in Difference Equations, 361, 1-16.
- 15. Huang, L., Guo, Z. and Wang, J. (2011) Theory and Applications of Differential Equations with Discontinuous Righthand Sides. Science Press, Beijing. (In Chinese)
- 16. Shi, R., Zhao, H. and Tang, S. (2014) Global Dynamic Analysis of a Vector-Borne Plant Disease Model. Advances in Difference Equations, 59, 1-16. https://doi.org/10.1186/1687-1847-2014-59
- 17. Filippov, A.F. (1988) Differential Equations with Discontinuous Righthand Sides. Mathematics and Its Applications (Soviet Series). Kluwer Academic, Boston. https://doi.org/10.1007/978-94-015-7793-9
- 18. Ma, Z. and Zhou, C. (2016) Methods of Qualitative and Stability of Ordinary Differential Equations. Science Press, Beijing. (In Chinese)
- 19. Baciotti, A. and Ceragioli, F. (1999) Stability and Stabilization of Discontinuous Systems and Non-Smooth Lyapunov Function. ESAIM: Control, Optimisation and Calculus of Variations, 4, 361-376. https://doi.org/10.1051/cocv:1999113












