Applied Mathematics
Vol.07 No.12(2016), Article ID:68983,6 pages
10.4236/am.2016.712114
The Effect of Variations in Ionic Conductance Values on the Dynamics of a Mathematical Model of Non-Spiking A-Type Horizontal Cells in the Rabbit Retina
Takaaki Shirahata
Institute of Neuroscience and Kagawa School of Pharmaceutical Sciences, Tokushima Bunri University, Sanuki, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2016; accepted 22 July 2016; published 25 July 2016
ABSTRACT
A previous study proposed a mathematical model of A-type horizontal cells in the rabbit retina. This model, which was constructed based on the Hodgkin-Huxley model, was described by a system of nonlinear ordinary differential equations. The model contained five types of voltage-depen- dent ionic conductances: sodium, calcium, delayed rectifier potassium, transient outward potassium, and anomalous rectifier potassium conductances. The previous study indicated that when the delayed rectifier potassium conductance had a small value, depolarizing stimulation could change the dynamic state of the model from a hyperpolarized steady state to a depolarized steady state. However, how this change was affected by variations in the ionic conductance values was not clarified in detail in the previous study. To clarify this issue, in the present study, we performed numerical simulation analysis of the model and revealed the differences among the five types of ionic conductances.
Keywords:
Mathematical Model, Numerical Simulation, A-Type Horizontal Cell, Ionic Conductance

1. Introduction
A-type horizontal cells in the rabbit retina are classified into two types: one type can generate repetitive spiking [1] , and the other cannot [2] . Mathematical modeling studies of these cells based on the Hodgkin-Huxley model have been reported (e.g., simulations of the spiking [2] [3] and nonspiking cells [2] ). Each of the mathematical models of the spiking and non-spiking cells is described by a system of nonlinear ordinary differential equations (ODEs), and contains five types of voltage-dependent ionic conductances: sodium, calcium, delayed rectifier potassium, transient outward potassium, and anomalous rectifier potassium conductances. However, the only difference between the mathematical models of the spiking and non-spiking cells is that the former takes a larger value of the delayed rectifier potassium conductance than the latter. In particular, a study by Aoyama et al. focused on the relationship between the dynamics of the non-spiking cell model and ionic conductances [2] . Although this study investigated the effect of a decrease in the sodium, calcium, and transient outward potassium conductances on the dynamics of the non-spiking cell model, it did not examine the effect of a decrease in other ionic conductances such as the anomalous rectifier potassium conductance. It also did not investigate the effect of an increase in the five types of ionic conductances. Detailed analysis of membrane conductance is very important [4] , and so it is necessary to systematically investigate the effect of not only a decrease but also an increase in the five types of ionic conductances on the dynamics of the non-spiking cell model. This systematic investigation will contribute to a detailed understanding of the characteristics of the ionic conductances of this model. Therefore, the present study performed numerical simulation to evaluate the effect of variations in the five types of ionic conductances on the dynamics of the non-spiking cell model.
2. Materials and Methods
The present study performed numerical simulations of a mathematical model of a rabbit A-type retinal horizontal cell that does not generate repetitive spiking (the non-spiking cell model), which was developed previously [2] . The model is described by a system of nonlinear ODEs, which consist of eight state variables: the membrane potential of the horizontal cell [V (mV)] and seven gating variables of ionic currents (mNa, hNa, mCa, mKv, hKv, mA, and hA). The time evolution of these state variables is described as follows:
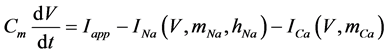
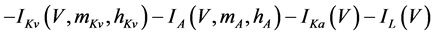 (1)
(1)
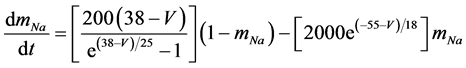 (2)
(2)
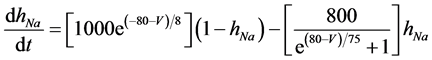 (3)
(3)
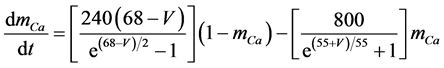 (4)
(4)
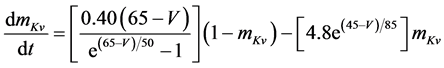 (5)
(5)
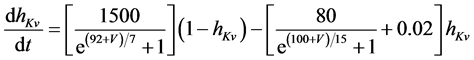 (6)
(6)
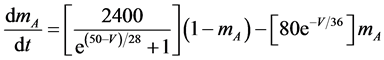 (7)
(7)
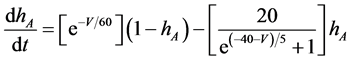 (8)
(8)
where Cm (=0.106 nF) is the membrane capacitance, Iapp is the externally injected current of constant amplitude, INa (V, mNa, hNa), ICa (V, mCa), IKv (V, mKv, hKv), IA (V, mA, hA), IKa (V), and IL (V) are the sodium, calcium, delayed rectifier potassium, transient outward potassium, anomalous rectifier potassium, and leakage currents, respectively, which are defined in the Equations (9)-(14) below.
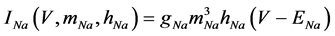 (9)
(9)
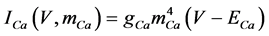 (10)
(10)
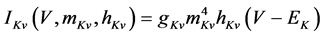 (11)
(11)
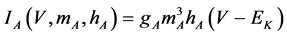 (12)
(12)
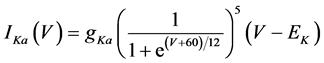 (13)
(13)
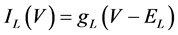 (14)
(14)
where gNa, gCa, gKv, gA, gKa, and gL (=0.5 nS) are the maximal conductances of INa (V, mNa, hNa), ICa (V, mCa), IKv (V, mKv, hKv), IA (V, mA, hA), IKa (V), and IL (V), respectively, ENa (=55 mV), ECa (=12.9log[2000/30] mV), EK (=−80 mV), and EL (=−80 mV) are the reversal potentials of INa (V, mNa, hNa), ICa (V, mCa), three types of potassium currents [i.e., IKv (V, mKv, hKv), IA (V, mA, hA), and IKa(V)], and IL (V), respectively. Refer to reference [2] for detailed explanations of the equations.
The free and open-source software Scilab (http://www.scilab.org/) was used to numerically solve the above ODEs (initial conditions: V = −80 mV, mNa = 0.026, hNa = 0.922, mCa = 0.059, mKv = 0.139, hKv = 0.932, mA = 0.030, and hA = 0.998). The total simulation time was 10 s in all the simulations. The values of the following system parameters were varied: Iapp, gNa, gCa, gKv, gA, and gKa. Iapp between 0.5 and 10 s was varied from 13 to 19 pA at an interval of 1 pA, while Iapp between 0.0 and 0.5 s was fixed to be zero. Default values of gNa, gCa, gKv, gA, and gKa were 2.4, 9.0, 4.5, 15.0, and 4.5 nS, respectively. Each ofgNa, gCa, gKv, gA, and gKa was varied to 50 or 150% of each default value.
3. Results
The previous study investigated the responses of the non-spiking cell model to depolarizing stimulations of different conditions [2] . In particular, the model does not show a positive potential in response to a stimulation of 10 pA, but does show one in response to a stimulation of 25 pA [2] . Based on these results, the present study first investigated in detail the responses of the model to depolarizing stimulations with amplitudes between these two values. In particular, the present study focused on the responses to stimulations between 13 and 19 pA under conditions in which all the ionic conductances were set to be default values. When the amplitudes were 13 and 14 pA, the model slightly depolarized, but it maintained a hyperpolarized steady state (i.e., it did not reach a positive potential) (Figure 1). In contrast, when the amplitudes were 15 pA or more, the model depolarized and finally reached a depolarized steady state (i.e., it did reach a positive potential) (Figure 1). In addition, the larger the amplitude, the faster the membrane potential reached a positive potential. Based on these results, the present study defined that the stimulation threshold for the induction of a positive potential was 15 pA.
The present study next investigated how variations in each ionic conductance value changed the stimulation threshold in order to reveal the relationship between the ionic conductances and the dynamics of the model. Figure 2 shows the influence of variations in the ionic conductance values on the dynamics of the model. Under conditions in which gNa was 50% of the default value with the other conductance values being default values, the model showed a hyperpolarized steady state in response to stimulations from 13 to 15 pA, but showed a depolarized steady state in response to stimulations from 16 to 19 pA. Therefore, the stimulation threshold for the induction of the positive potential was 16 Pa at 50% gNa. Similarly, the thresholds under different gNa conditions were calculated: the threshold at 100% gNa and 150% gNa was 15 pA. The thresholds under conditions in which the other ionic conductance values were varied were also calculated in a similar manner. The threshold was 19 pA at 50% gCa, 15 pA at 100% gCa, and 14 pA at 150% gCa. The threshold was 15 pA at 50% gKv, 15 pA at 100% gKv, and 16 pA at 150% gKv. The threshold was 15 pA at 50% gA, 15 pA at 100% gA, and 16 pA at 150% gA. The threshold was 15 pA at 50% gKa, 15 pA at 100% gKa, and 17 pA at 150% gKa.
4. Discussion
The present study performed numerical simulation of a mathematical model of a non-spiking A-type horizontal
Figure 1. Time courses of the membrane potential of the model. The responses of the model to the stimulation of various amplitudes (from 13 to 19 pA) are superimposed. The stimulation was applied between 0.5 and 10 s, but not between 0 and 0.5 s.
Figure 2. The dependence of the dynamical states of the model on Iapp and gx (x = Na, Ca, Kv, A, and Ka). ○ indicates a hyperpolarized steady state, whereas ● indicates a depolarized steady state.
cell in the rabbit retina, and revealed the sensitivity of the stimulation threshold for the transition from a hyperpolarized steady state to a depolarized steady state to variations in ionic conductance values. A previous study investigated the effect of variations in ionic conductance values on the dynamics of the model [2] . However, this study was limited to the analyses of the effect of the elimination of the sodium and calcium conductances and the effect of a decrease in the transient outward potassium conductance [2] . Therefore, the study did not reveal the effect of variations in other ionic conductances such as the anomalous rectifier potassium conductance. Moreover, the previous study did not reveal the effect of an increase in the ionic conductances. To overcome these limitations, the present study not only decreased but also increased all the voltage-dependent ionic conductances, and revealed these effects on the model. Increases in gNa and gCa induced a decrease in the stimulation threshold, whereas increases in gKv, gA, and gKa induced an increase in the stimulation threshold (Figure 2). In addition, the sensitivity of the stimulation threshold to variations in the ionic conductance values was in the order of gCa > gKa > gNa = gKv = gA. In particular, the present study revealed that the influence of gKa on the stimulation threshold was the largest among the three types of potassium conductances (i.e., gKv, gA, and gKa). This is an important finding, which has not been reported previously.
Analyses of mathematical models of other retinal cells based on the Hodgkin-Huxley model have been performed previously (e.g., in a retinal ganglion cell model [5] and a retinal amacrine cell model [6] ). However, in contrast to the nonspiking cell model of the present study, these studies focused on a repetitive spiking behavior observed in ganglion [5] and amacrine [6] cells.
Previous studies of other neuron models have reported the relationship between the stimulation threshold and ionic conductances (e.g., a vibrissa motoneuron model [7] , an electrosensory neuron model [8] , and a medial vestibular nucleus neuron (mVNn) model [9] ). In particular, although the vibrissa motoneuron and electrosensory neuron models do not include calcium conductance, the mVNn model does. A previous study of the mVNn model [9] illustrated that (1) calcium conductance influences the dynamical states of the mVNn model linearly, and (2) an increase in calcium conductance increases the stimulation threshold for the transition to a more excitable state (i.e., the transition from a hyperpolarized steady state to a repetitive spiking state). In contrast, the present study (Figure 2) showed that (1) calcium conductance influenced the dynamical states of the nonspiking horizontal cell model nonlinearly, and (2) an increase in calcium conductance decreased the stimulation threshold for the transition to a more excitable state (i.e., the transition from a hyperpolarized steady state to a depolarized steady state).
5. Conclusion
The present study performed numerical simulation of a model of a nonspiking A-type horizontal cell in the rabbit retina to reveal the effect of variations in ionic conductances on the dynamics of the model. In particular, the present study revealed that (1) the calcium conductance affected the dynamical states of the model highly nonlinearly, and (2) the anomalous rectifier potassium conductance had the largest influence on the changes in the stimulation threshold among the three types of potassium conductances. Neither of these details has been reported previously. The present study contributes to a more detailed understanding of the characteristics of the ionic conductances of the model.
Acknowledgements
The author would like to thank Enago (www.enago.jp) for their review of the English language.
Cite this paper
Takaaki Shirahata, (2016) The Effect of Variations in Ionic Conductance Values on the Dynamics of a Mathematical Model of Non-Spiking A-Type Horizontal Cells in the Rabbit Retina. Applied Mathematics,07,1297-1302. doi: 10.4236/am.2016.712114
References
- 1. Blanco, R., Vaquero, C.F. and de la Villa, P. (1996) Action Potentials in Axonless Horizontal Cells Isolated from the Rabbit Retina. Neuroscience Letters, 203, 57-60.
http://dx.doi.org/10.1016/0304-3940(95)12263-X - 2. Aoyama, T., Kamiyama, Y., Usui, S., Blanco, R., Vaquero, C.F. and de la Villa, P. (2000) Ionic Current Model of Rabbit Retinal Horizontal Cell. Neuroscience Research, 37, 141-151.
http://dx.doi.org/10.1016/S0168-0102(00)00111-5 - 3. Shirahata, T. (2008) Simulation of Rabbit A-Type Retinal Horizontal Cell That Generates Repetitive Action Potentials. Neuroscience Letters, 439, 116-118.
http://dx.doi.org/10.1016/j.neulet.2008.04.087 - 4. Ashrafuzzaman, M. and Tuszynski, J. (2012) Membrane Biophysics. Springer, Heidelberg, 26.
- 5. Fohlmeister, J.F., Cohen, E.D. and Newman, E.A. (2010) Mechanisms and Distribution of Ion Channels in Retinal Ganglion Cells: Using Temperature as an Independent Variable. Journal of Neurophysiology, 103, 1357-1374.
http://dx.doi.org/10.1152/jn.00123.2009 - 6. Cembrowski, M.S., Logan, S.M., Tian, M., Jia, L., Li, W., Kath, W.L., Riecke, H. and Singer, J.H. (2012) The Mechanisms of Repetitive Spike Generation in an Axonless Retinal Interneuron. Cell Reports, 1, 155-166.
http://dx.doi.org/10.1016/j.celrep.2011.12.006 - 7. Golomb, D. (2014) Mechanism and Function of Mixed-Mode Oscillations in Vibrissa Motoneurons. PLoS ONE, 9, e109205.
http://dx.doi.org/10.1371/journal.pone.0109205 - 8. Shirahata, T. (2016) The Relationship of Sodium and Potassium Conductances with Dynamic States of a Mathematical Model of Electrosensory Pyramidal Neurons. Applied Mathematics, 7, 819-823.
http://dx.doi.org/10.4236/am.2016.79072 - 9. Shirahata, T. (2016) The Effect of Variations in Ionic Conductance Values on the Suppression of Repetitive Spiking in a Mathematical Model of Type-A Medial Vestibular Nucleus Neurons. Applied Mathematics, 7, 1134-1139.
http://dx.doi.org/10.4236/am.2016.710101



