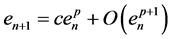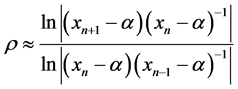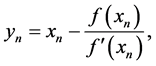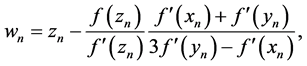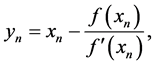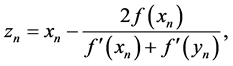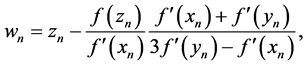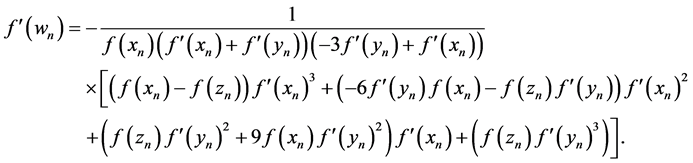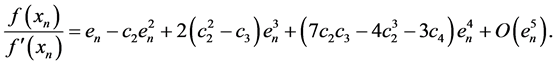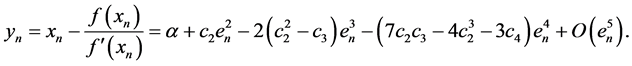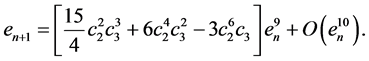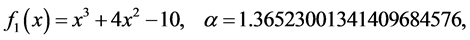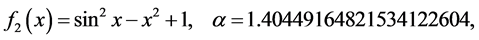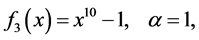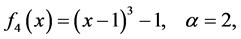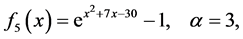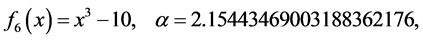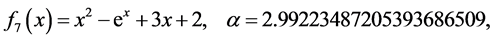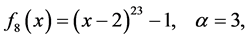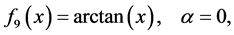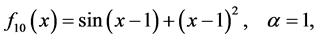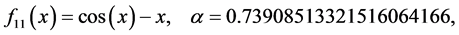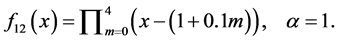Applied Mathematics
Vol.07 No.06(2016), Article ID:64928,9 pages
10.4236/am.2016.76043
A New Approach for Solving Nonlinear Equations by Using of Integer Nonlinear Programming
Armin Ghane-Kanafi, Sohrab Kordrostami
Department of Mathematics, Lahijan Branch, Islamic Azad University, Lahijan, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 January 2016; accepted 21 March 2016; published 24 March 2016
ABSTRACT
One of the most important issues in numerical calculations is finding simple roots of nonlinear equations. This topic is one of the oldest challenges in science and engineering. Many important problems in engineering, to achieve the result need to solve a nonlinear equation. Thus, the formulation of a recursive relationship with high order of convergence and low time complexity is very important. This paper provides a modification to the Weerakoon-Fernando and Parhi-Gupta methods. It is shown that, in each iterate, the improved method requires three evaluations of the function and two evaluations of the first derivatives of function. The proposed with the Kou et al., Neta, Parhi-Gupta, Thukral and Mir et al. methods have been applied to a collection of 12 test problem. The results show that proposed approach significantly reduces the number of function calls when compared to the above methods. The numerical examples show that the proposed method is more efficiency than other methods in this class, such as sixth-order method of Parhi-Gupta or eighth-order method of Mir et al. and Thukral. We show that the order of convergence the proposed method is 9 and also, the modified method has the efficiency of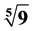 .
.
Keywords:
Newton Method, Nonlinear Equations, Convergence Theorem, Efficiency Index

1. Introduction
In the real world, many of the complex problems after simplification lead to solving nonlinear problems. Find an approximation of the simple roots of the equations is one of the important problems on this issue. The rapid development of technology has led to different of algorithms. Over time, many algorithms have been developed. In this state, one of the ways for comparison of different algorithms is finding of complexity of time and index efficiency of algorithms. MAPLE software is one of the powerful algebraic systems from Maplesoft company, such that in this article it has been used for the calculation. The boundary value problems appearing in kinetic theory of gases, elasticity and other applied areas are reduced to solve these equations. Many optimization problems also lead such equations. Hence, one of the most important problems in numerical analysis is to find a simple root a of a nonlinear equation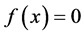 , where
, where  for an open interval
for an open interval  is a scalar function. In this study, in order to find a, we should start with an initial approximation
is a scalar function. In this study, in order to find a, we should start with an initial approximation 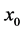 which is near to the root and generates successive iterates
which is near to the root and generates successive iterates 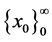 converging to simple root a of nonlinear equation
converging to simple root a of nonlinear equation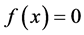 . In all iteration, the improved method requires three evaluations of the function and two evaluations of the first order derivatives of function. Therefore, the modified method has the efficiency index
. In all iteration, the improved method requires three evaluations of the function and two evaluations of the first order derivatives of function. Therefore, the modified method has the efficiency index . The numerical examples show that, the proposed method has more efficient with respect to the Newton method and other methods in this class. The effectiveness of the modified ninth-order method will be examined by approximation the simple root of a given non-linear equation. The suggested method is comparable to the sixth-order methods [1] [2] ; also the eighth-order methods [3] and [4] .
. The numerical examples show that, the proposed method has more efficient with respect to the Newton method and other methods in this class. The effectiveness of the modified ninth-order method will be examined by approximation the simple root of a given non-linear equation. The suggested method is comparable to the sixth-order methods [1] [2] ; also the eighth-order methods [3] and [4] .
In the reminder, we proceed as follows: In Section 2, we recall the basic concepts. The proposed method is described in Section 3. In Section 4, the convergence analysis is carried out to establish the ninth-order of convergence of our method. In Section 5, as is shown in the numerical examples, this method is more efficient than Newton method and other methods of lower or same order. We conclude with some remarks on the presented approaches in Section 6.
2. Several Basic Definitions
Our goal is to find the value of x that satisfies the following equation.
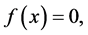 (1)
(1)
where 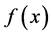 is a nonlinear equation. The value of x that satisfies (1) is called a root of
is a nonlinear equation. The value of x that satisfies (1) is called a root of 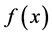 and denoted by a. Therefore, the procedure used of to find x is called root-finding. Let a is a simple root of Equation (1) and
and denoted by a. Therefore, the procedure used of to find x is called root-finding. Let a is a simple root of Equation (1) and 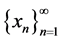 is a real sequence.
is a real sequence.
Definition 1. See [5] : The sequence 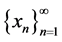 is said to converge to a if
is said to converge to a if
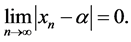
Furthermore, if there exists positive constant c and p such that:
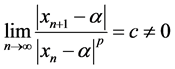
we say that 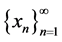
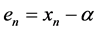
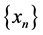
is called the error equation. The value of p is called the order of convergence of method, see [6] .
Definition 2. Let a be a root of the function f and suppose that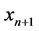
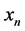
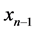
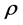
3. New Proposed Scheme
The new method is based on [2] method. With a simple manipulation, and a new approach to get the following equations.
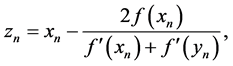
and
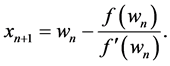
This is four-step method. It is not necessary to compute the first-order derivative at the point 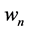
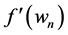
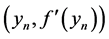
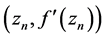
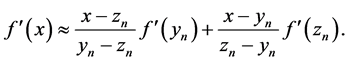
Therefore,
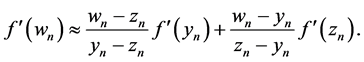
Now using Equations (2), we have:
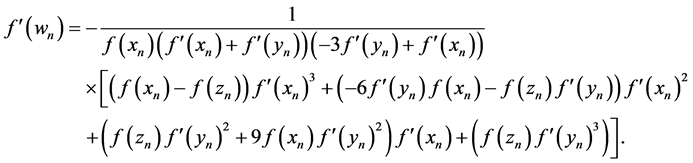
Substituting the relation of (6) into the relation (3), in this case, we obtain the following formula:
where,
Obviously this method requires evaluations of three function f and two derivatives
4. Convergence Analysis
To determine order of convergence of proposed method, we must be solving integer nonlinear programming as follow:
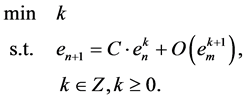
where C is a special coefficient of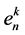
Theorem 1. Let 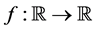
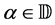
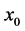
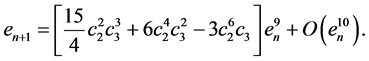
where 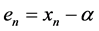
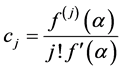
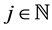
Proof. Let 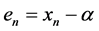
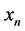
and
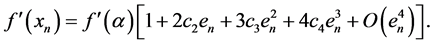
Quotient relations (9) and (10), gives the following results:
Thus we have
Taylor expansion of the function 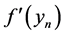
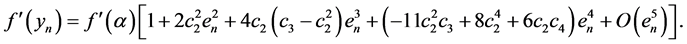
Substituting (9), (10) and (11) into the zn section of the Equation (2), we have:
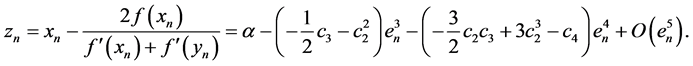
Furthermore, the Taylor expansion of 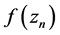
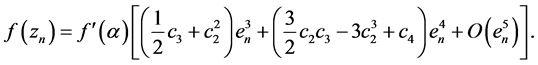
Since from (10), (12) and (13) we get:
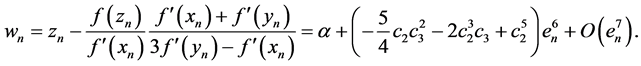
Again, using the Taylor expansion of function 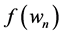
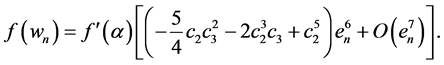
Taylor expansion of the function 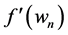
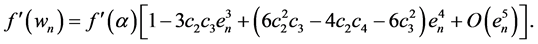
In this case, using the above result (i.e (15), (16) and (14)) and corresponding to the relation (3), we get:
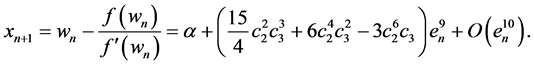
Therefore, we have:
Thus, the ninth order of convergence of the method is established.
Numerical Examples
In order to demonstrate the performance, accuracy and effectiveness of the proposed ninth-order method, we take 12 special nonlinear equation test problems from [2] [7] and [8] . We compare the proposed method with Wang-Liu’s third-order method [8] , Weerakoon-Fernando and Parhi-Gupta’s sixth-order methods [1] [2] and Kou et al. and Neta’s eight-order methods as [3] and [4] , respectively. The computing results displayed in Tables 1-5. In every problem we try to seek an approximation 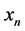
Table 1. Comparison of result of proposed method (PM) with Kou and Li (KL) method.
Table 2. Comparison of result of proposed method (PM) with Parhi and Gupta (PG) method.
Table 3. Comparison of result of proposed method (PM) with Neta (NM) method.
Table 4. Comparison of result of proposed method (PM) with Thaukral (TM) method.
Table 5. Comparison of result of proposed method (PM) with Mir (MM) method.
iteration. In this paper, the stoping criterion is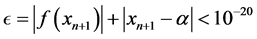
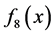
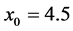
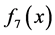
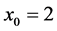
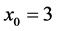
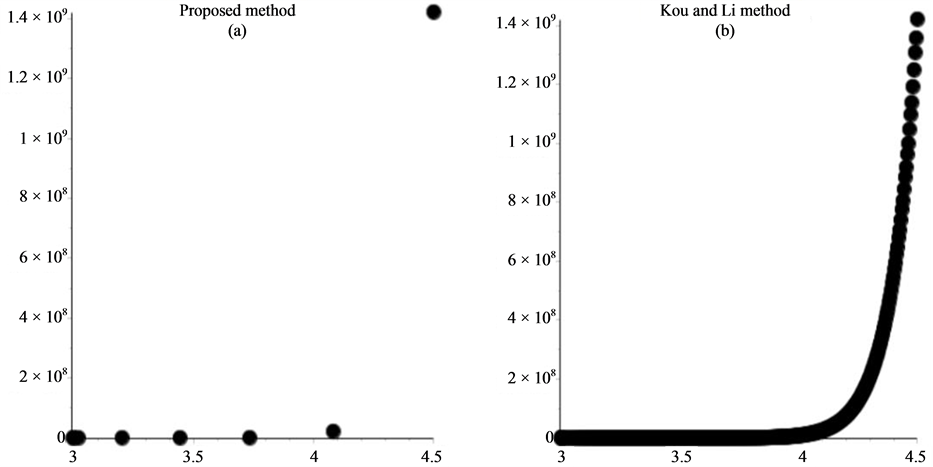
The test functions are listed as follows:
Figure 1. A comparison of the rate of convergence of the proposed method and Kou et al. method for function 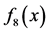
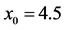
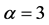
One can easily see from Tables 1-5 that our method behaves either similarly or better then the compared methods. The results show that the new method has advantages over the Kou et al. [8] method and the eight-order method as Thukral [4] method. Also, the new method have iteration stabilities to the original iteration value and behave either similarly or better than the methods compared. All numerical results are in accordance with the theory and the basic advantage of the variants of Newton’s method based on means or integration methods that they do not require the computation of second- or higher-order derivatives although they are of ninth order.
5. Conclusion
In numerical analysis, many methods produce sequences of real numbers, for example the iterative schemes for solving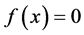
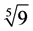
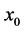
Cite this paper
ArminGhane-Kanafi,SohrabKordrostami, (2016) A New Approach for Solving Nonlinear Equations by Using of Integer Nonlinear Programming. Applied Mathematics,07,473-481. doi: 10.4236/am.2016.76043
References
- 1. Neta, B. (1979) A Sixth-Order Family of Methods for Nonlinear Equations. International Journal of Computer Mathematics, 7, 157-161.
http://dx.doi.org/10.1080/00207167908803166 - 2. Parhi, S.K. and Gupta, D.K. (2008) A Sixth Order Method for Nonlinear Equations. Applied Mathematics and Computation, 203, 50-55.
http://dx.doi.org/10.1016/j.amc.2008.03.037 - 3. Mir, N.A., Rafiq, N. and Akram, S. (2009) An Efficient Three-Step Iterative Method for Non-Linear Equations. International Journal of Mathematical Analysis, 3, 1989-1996.
- 4. Thukral, R. (2010) A New Eighth-Order Iterative Method for Solving Nonlinear Equations. Applied Mathematics and Computation, 217, 222-229.
http://dx.doi.org/10.1016/j.amc.2010.05.048 - 5. Wait, R. (1979) The Numerical Solution of Algebraic Equations.
- 6. Weerakoon, S. and Fernando, T.G.I. (2000) A Variant of Newton’s Method with Accelerated Third-Order Convergence. Applied Mathematics Letters, 13, 87-93.
http://dx.doi.org/10.1016/S0893-9659(00)00100-2 - 7. Wang, X. and Liu, X.P. (2009) Two New Families of Sixth-Order Methods for Solving Non-Linear Equations. Applied Mathematics and Computation, 213, 73-78.
http://dx.doi.org/10.1016/j.amc.2009.03.007 - 8. Kou, J.S., Li, Y.T. and Wang, X.H. (2006) A Medication of Newton Method with Third-Order Convergence. Applied Mathematics and Computation, 181, 1106-1111.
http://dx.doi.org/10.1016/j.amc.2006.01.076
NOTES
1Since the proposed method in this paper is the revised and generalized form of the Newton method, it consist of common problems in New- ton method such as proper selection of initial point. In order to solve this problem we can use a number of repetitions of ever-convergence methods as Bisection or False-position.