Applied Mathematics
Vol.06 No.14(2015), Article ID:62143,8 pages
10.4236/am.2015.614197
Reflected BSDEs Driven by Lévy Processes and Countable Brownian Motions
Jean-Marc Owo
UFR de Mathématiques et Informatique, Université Félix H. Boigny, Abidjan, Côte d’Ivoire
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2015; accepted 20 December 2015; published 23 December 2015
ABSTRACT
A new class of reflected backward stochastic differential equations (RBSDEs) driven by Teugels martingales associated with Lévy process and Countable Brownian Motions are investigated. Via approximation, the existence and uniqueness of solution to this kind of RBSDEs are obtained.
Keywords:
Backward Doubly Stochastic Differential Equations, Lévy Processes, Teugels Martingales, Countable Brownian Motions

1. Introduction
Recently, Y. Ren [1] proved via the Snell envelope and the fixed point theorem, the existence and uniqueness of a solution for the following RBDSDEs driven by a Lévy process and a extra Brownian motion with Lipschitz coefficients, where the obstacle process is right continuous with left limits (càdlàg):
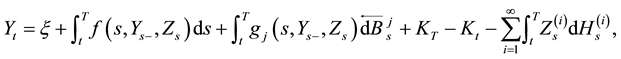
where the 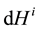 is a forward semi-martingale Itô integrals (see He et al. [2] ) and the
is a forward semi-martingale Itô integrals (see He et al. [2] ) and the 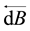 is a backward Itô integral.
is a backward Itô integral.
Note that, in all the previous works, the equations are driven by finite Brownian motions. In their recent work, Pengju Duan et al. [3] introduced firstly the reflected BDSDEs driven by countable extra Brownian motions:
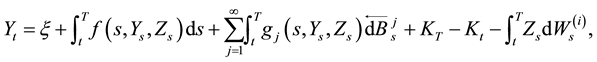 (1.1)
(1.1)
where the dW is the standard forward stochastic Itô integral and the 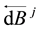 is the backward stochastic Itô integral. Under the global Lipschitz continuity conditions on the coefficients f and g, they proved via Snell envelope and fixed point theorem, the existence and uniqueness of the solution for RBDSDEs (1.1). Next, J.-M. Owo [4] relaxed the Lipschitz continuity condition on the coefficient f to a continuity with sub linear growth condition and derive the existence of minimal and maximal solutions to RBSDEs (1.1).
is the backward stochastic Itô integral. Under the global Lipschitz continuity conditions on the coefficients f and g, they proved via Snell envelope and fixed point theorem, the existence and uniqueness of the solution for RBDSDEs (1.1). Next, J.-M. Owo [4] relaxed the Lipschitz continuity condition on the coefficient f to a continuity with sub linear growth condition and derive the existence of minimal and maximal solutions to RBSDEs (1.1).
Motivated by [1] [3] [4] , in this paper, we mainly consider the following RBDSDEs driven by a Lévy process and countable Brownian motions, in which the obstacle process is right continuous with left limits (càdlàg):
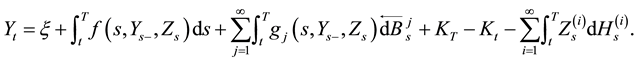 (1.2)
(1.2)
The paper is devoted to prove the existence and uniqueness of a solution for RBSDEs driven by a Lévy process and countable Brownian motions.
The paper is organized as follows. In section 2, we give some preliminaries and notations. In section 3, we establish the main results.
2. Preliminaries and Notations
Throughout this paper, T is a positive constant and  is a probability space on which,
is a probability space on which,  are mutual independent one-dimensional standard Brownian motions and
are mutual independent one-dimensional standard Brownian motions and  be a
be a  -valued pure jump Lévy process of the form
-valued pure jump Lévy process of the form  independent of
independent of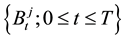 , which correspond to a standard Lévy
, which correspond to a standard Lévy
measure 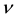 satisfying
satisfying 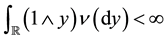 and
and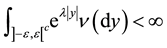 , for every
, for every 

Let 


where for any process


Note that 

collection 
Let us introduce some spaces:
・ 





・ 


・ 





・ 






・ 

We will denote by 



In the sequel, for ease of notation, we set
Furthermore, we denote by 

where 






In [5] , Nualart and Schoutens proved that the coefficients 






Definition 2.1. A solution of a (1.2) is a triplet of 

1)
2)
3) K is a continuous and increasing process with 
Throughout the paper, we let the coefficients 



(H1) for all


(H2) for all 

where




(H3)



(H4) S is a real-valued, càdàg process such that 



with

stopping times (see He et al. [2] ).
3. The Main Results
We first establish the existence and uniqueness result for RBSDEs driven by finite Brownian motions and a Lévy process:

For any
Lemma 3.2. Assume (H1) - (H4). Then, there exists a unique solution 
Proof. For







respectively by 








Now, we are ready to establish the main result of this paper which is the following theorem.
Theorem 3.3. Under assumptions (H1)-(H4), there exists a unique solution 
Proof. (Existence.) By Lemma 3.1, for any



The idea consists to study the convergence of the sequence

where 

From assumption (H2) and Young’s inequality, for any 
Using again Young inequality, we have for any
Since
we have, for any
Therefore,
Consequently,
We choose 


Applying Gronwall’s inequality, we get
Therefore, we have the existence of a constant 
which by Burkhölder-Davis-Gundy’s inequality provides
Now, we show that 



Applying Itô’s formula to

Taking expectation in both side of (3.5) and noting that

Using again Young’s inequality, assumption (H2) and the estimates (3.3), we obtain,
where
Therefore, by Gronwall’s inequality, we have
which, by Burkholder-Davis-Gundy inequality provides
Well, from assumptions (H1)-(H2), we have
Consequently, we get,

Moreover, from (3.4) together with Hölder’s and Burkholder-Davis-Gundy’s inequalities, we have
which, together with assumption (H2) and (3.7), provides

Consequently, 



Now, let us show that the process 
Also, by Burkhölder-Davis-Gundy’s inequality, we get
and
Now, from (H1)-(H2) and the fact that
which implies that
Moreover,
Therefore,
On the other hand, from the result of Saisho [6] (see p. 465), we have
Finally, passing to the limit in (3.2), we conclude that 
(Uniqueness.) Let 

Applying Itô’s formula to

Taking expectation in both side of (3.10) and noting that

Using again Young’s inequality 
Choosing




On the other hand, since,
we have

Cite this paper
Jean-MarcOwo, (2015) Reflected BSDEs Driven by Lévy Processes and Countable Brownian Motions. Applied Mathematics,06,2240-2247. doi: 10.4236/am.2015.614197
References
- 1. Ren, Y. (2010) Reflected Backward Doubly Stochastic Differential Equations Driven by a Lévy Process. C. R. Acad. Sci. Paris, Ser. I, 348, 439-444.
- 2. Yan, J., He, S. and Wang, J. (1995) Semimartingale and Stochastic Analysis. Scientific Press, Beijing,
- 3. Duan, P.J., Ren, M. and Fei, S.L. (2013) Reflected Backward Stochastic Differential Equations Driven by Countable Brownian Motions. Journal of Applied Mathematics, 2013, Article ID: 729636.
- 4. Owo, J.-M. (2015) Reflected Backward Stochastic Differential Equations Driven by Countable Brownian Motions with Continuous Coefficients. Electronic Communications in Probability, 20, 1-11.
http://dx.doi.org/10.1214/ECP.v20-3771 - 5. Nualart, D. and Schoutens, W. (2001) Backward Stochastic Differential Equations and Feynman-Kac Formula for Lévy Processes with Applications in Finance. Bernoulli, 7, 761-776.
http://dx.doi.org/10.2307/3318541 - 6. Saisho, Y. (1987) SDE for Multidimensional Domains with Reflecting Boundary. Probability Theory and Related Fields, 74, 455-477.
http://dx.doi.org/10.1007/BF00699100






































