Applied Mathematics
Vol.06 No.03(2015), Article ID:54504,9 pages
10.4236/am.2015.63044
Boundary Layer Stagnation-Point Slip Flow and Heat Transfer towards a Shrinking/Stretching Cylinder over a Permeable Surface
Nor Azian Aini Mat1, Norihan Md. Arifin2*, Roslinda Nazar3, Norfifah Bachok4
1Faculty of Science and Mathematics, Universiti Pendidikan Sultan Idris, Perak, Malaysia
2Institute for Mathematical Research, Universiti Putra Malaysia, Selangor, Malaysia
3School of Mathematical Sciences, Universiti Kebangsaan Malaysia, Selangor, Malaysia
4Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, Selangor, Malaysia
Email: *norihanarifin@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 February 2015; accepted 4 March 2015; published 10 March 2015
ABSTRACT
In this paper, the boundary layer stagnation-point slip flow and heat transfer towards a shrinking/stretching cylinder over a permeable surface is considered. The governing equations are first transformed into a system of non-dimensional equations via the non-dimensional variables, and then into self-similar ordinary differential equations before they are solved numerically using the shooting method. Numerical results are obtained for the skin friction coefficient and the local Nusselt number as well as the velocity and temperature profiles for some values of the governing parameters, namely the velocity slip parameter , the thermal slip parameter
, the thermal slip parameter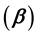 , the curvature parameter
, the curvature parameter 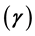 and the velocity ratio parameter
and the velocity ratio parameter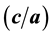 . The physical quantities of interest are the skin friction coefficient and the local Nusselt number measured by
. The physical quantities of interest are the skin friction coefficient and the local Nusselt number measured by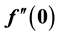 and
and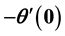 , respectively. The numerical results show that the velocity slip parameter
, respectively. The numerical results show that the velocity slip parameter 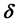 increases the heat transfer rate at the surface, while the thermal slip parameter
increases the heat transfer rate at the surface, while the thermal slip parameter 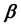 decreases it. On the other hand, increasing the velocity slip parameter
decreases it. On the other hand, increasing the velocity slip parameter 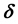 causes the decrease in the flow velocity. Further, it is found that the solutions for a shrinking cylinder
causes the decrease in the flow velocity. Further, it is found that the solutions for a shrinking cylinder 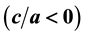 are non-unique with dual solutions, which is different from a stretching cylinder
are non-unique with dual solutions, which is different from a stretching cylinder  case. Finally, it is also found that the values of
case. Finally, it is also found that the values of 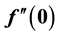 and
and  increase as the curvature parameter
increase as the curvature parameter 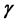 increases.
increases.
Keywords:
Boundary Layer, Heat Transfer, Numerical Solution, Shrinking/Stretching Cylinder, Slip Flow, Stagnation-Point, Suction/Injection

1. Introduction
The problem of flow and heat transfer induced by continuous shrinking or stretching surfaces has received considerable attention in recent years because it is an important type of flow occurring in many engineering disciplines. The stagnation point flow problems have been extensively studied by several authors. The problem of flow due to a shrinking or stretching sheet has been later extended to many flow situations. Crane [1] was the first studied the steady boundary layer flow of a viscous fluid due to a linearly stretching surface. Later, Chiam [2] extended the works of Crane [1] to stagnation-point flow over a stretching sheet. Wang [3] first investigated the stagnation-point flow towards a shrinking sheet for both two-dimensional and axiymmetric cases. He found that problem have the dual solutions as well as unique solution for a specific values of the ratio of shrinking.
The problem of unsteady stagnation-point flow of a viscous and incompressible fluid by considering both the stretching and shrinking sheet situations have been investigated by Fan et al. [4] . On the other hand, Bachok et al. [5] discussed the effect of melting on boundary layer stagnation-point flow towards a stretching or shrinking sheet. Ahmad et al. [6] investigated the behaviour of the steady boundary layer flow and heat transfer of a micropolar fluid near the stagnation point on a stretching vertical surface with prescribed skin friction. Lok et al. [7] studied the steady axisymmetric stagnation point flow of a viscous and incompressible fluid over a shrinking circular cylinder with mass transfer (suction). Bhattacharyya et al. [8] analyzed the effects of partial slip on the steady boundary layer stagnation-point flow of an incompressible fluid and heat transfer towards a shrinking sheet. This investigation explores the conditions of the non-existence, existence, uniqueness and duality of the solutions of self-similar equations numerically. They also studied the same case but under the condition of unsteady-state towards a stretching. Stagnation-point flow and heat transfer over an exponentially shrinking sheet was analyzed by Bhattacharyya and Vajravelu [9] . They obtained dual solutions for the velocity and the temperature fields and also they observed that their boundary layers are thinner for the first solution.
Therefore, the present investigation deals with the effects of partial slip on the boundary layer stagnation- point flow and heat transfer towards a shrinking/stretching cylinder over a permeable surface.
2. Problem Formulation
Consider the steady stagnation-point flow towards a horizontal linearly stretching/shrinking cylinder with radius 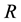 placed in an incompressible viscous fluid of constant temperature
placed in an incompressible viscous fluid of constant temperature . Using boundary layer approximation, the equations of motion and temperature distribution may be written in usual notations as below
. Using boundary layer approximation, the equations of motion and temperature distribution may be written in usual notations as below



where 







The appropriate boundary conditions for the velocity components with partial slip condition at the wall and for the temperature are given by


where 











Next, we introduce the transformation as follows:

where 




of suction and injection, we have consider that 
where 





subject to the boundary conditions (5) and (6) which become

where 


and 


The main physical quantities of interest are the value of











3. Results and Discussion
Equations (8) and (9) with the boundary conditions (10) are solved numerically using the shooting method. Table 1 shows the variations of 






Table 1. Variations of 





pared the present results obtained with those of Bhattacharyya et al. [8] for 























increasing

















Figure 5 shows the variations of 

































Figure 9 and Figure 10 represent the variations of 










similar as 
















field boundary conditions asymptotically. Further, these figures also support the existence of dual nature of the solutions as presented in the earlier figures where the boundary layer thickness for the first solution is smaller than that of the second solution.
Figure 1. Variations of 






Figure 2. Variations of 






Figure 3. Variations of 






Figure 4. Variations of 






Figure 5. Variations of 






Figure 6. Variations of 






Figure 7. Variations of 






Figure 8. Variations of 






Figure 9. Variations of 






Figure 10. Variations of 






Figure 11. Velocity profiles 






Figure 12. Temperature profiles 






Figure 13. Velocity profiles 






Table 2. Variations of 






Figure 14. Temperature profiles 






4. Conclusion
The study of boundary layer stagnation-point slip flow and heat transfer towards a shrinking/stretching cylinder over a permeable surface has been investigated numerically using the shooting method. Comparisons of the present results with those of Bhattacharyya et al. [8] are in excellent agreement. The velocity slip parameter 






Acknowledgements
The authors gratefully acknowledged the financial support received in the form of a FRGS research grant from the Ministry of Education, Malaysia.
Cite this paper
Nor Azian AiniMat,Norihan Md.Arifin,RoslindaNazar,NorfifahBachok, (2015) Boundary Layer Stagnation-Point Slip Flow and Heat Transfer towards a Shrinking/Stretching Cylinder over a Permeable Surface. Applied Mathematics,06,466-475. doi: 10.4236/am.2015.63044
References
- 1. Crane, L.J. (1970) Flow Past a Stretching Plate. ZAMP, 21, 645-647.
http://dx.doi.org/10.1007/BF01587695 - 2. Chiam, T.C. (1994) Stagnation-Point Flow towards a Stretching Plate. Journal of Physical Society of Japan, 63, 2443-2444.
http://dx.doi.org/10.1143/JPSJ.63.2443 - 3. Wang, C.Y. (2008) Stagnation Flow towards a Shrinking Sheet. International Journal of Non-Linear Mechanics, 43, 377-382.
http://dx.doi.org/10.1016/j.ijnonlinmec.2007.12.021 - 4. Fan, T., Xu, H. and Pop, I. (2010) Unsteady Stagnation Flow and Heat Transfer towards a Shrinking Sheet. International Communications in Heat and Mass Transfer, 37, 1440-1446.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2010.08.002 - 5. Bachok, N., Ishak, A. and Pop, I. (2010) Melting Heat Transfer in Boundary Layer Stagnation-Point Flow towards a Stretching/Shrinking Sheet. Physics Letters A, 374, 4075-4079.
http://dx.doi.org/10.1016/j.physleta.2010.08.032 - 6. Ahmad, K., Nazar, R. and Pop, I. (2011) Boundary Layer Flow and Heat Transfer of a Micropolar Fluid near The Stagnation Point on a Stretching Vertical Surface with Presribed Skin Friction. International Journal of Minerals, Metallurgy and Materials, 18, 502-507.
http://dx.doi.org/10.1007/s12613-011-0469-y - 7. Lok, Y.Y., Ishak, A. and Pop, I. (2011) MHD Stagnation Point Flow with Suction towards a Shrinking Sheet. Sains Malaysiana, 40, 1179-1186.
- 8. Bhattacharyya, K., Mukhopadhyay, S. and Layek, G.C. (2011) Slip Effects on Boundary Layer Stagnation-Point Flow and Heat Transfer towards a Shrinking Sheet. International Journal of Heat and Mass Transfer, 54, 308-331.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.09.041 - 9. Bhattacharyya, K. and Vajravelu, K. (2012) Stagnation-Point Flow and Heat Transfer over an Exponentially Shrinking Sheet. Communications in Nonlinear Science and Numerical Simulation, 17, 2728-2734.
NOTES
*Corresponding author.


















