Received 9 January 2015; accepted 27 January 2015; published 3 February 2015

ABSTRACT

In this paper, a tri-dimensional filter method for nonlinear programming was proposed. We add a parameter into the traditional filter for relaxing the criterion of iterates. The global convergent properties of the proposed algorithm are proved under some appropriate conditions.

Keywords:

Tri-Dimensional, NCP Function, Global Convergence, QP-Free

1. Introduction

This paper is concerned with finding a solution of a Nonlinear Programming (NLP) problem, as following

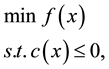(1)

where, 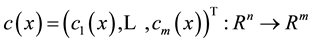are second-order continuously differentiable. The Lagrangian function associated with problem (1) is the function

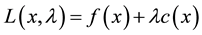
where is the multiplier vector. For simplicity, we denote the column vector as. A point is called a Karush-Kuhn-Tucker (KKT) point if it satisfies the following conditions:

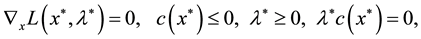(2)

we also say that is a KKT point of problem (1) if there exists a 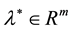such that 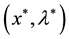satisfied (2).

Traditionally, this question has been answered by using penalty function. But it is difficult to find a suitable penalty parameter. In order to avoid the pitfalls of penalty function, Nonlinear programming problems (NLP) filter methods were first proposed by Fletcher in a plenary talk at the SIAM Optimization Conference in Victoria in May 1996; the methods are described in [1] . And soon, Global convergence proof of filter method was given in [2] . Because of good global convergence and numerical results, filter methods have quickly become popular in other areas such as nonsmooth optimization, nonlinear equations and so on [3] [4] .

Motivated by the ideas of filter methods above, a tri-dimensional filter method for nonliner programming was proposed as acceptance criterion to judge whether to accept a trial step in our algorithm. We have following advantages:

1) By enhancing the flexibility of filter, motivated by [5] , we increase a dimension by introducing a parameter to relax the criterion of iterates.

2) The Maratos effect that makes good progress toward the solution may be rejected and has been avoided by using tri-dimensional filter method as acceptance criterion.

3) Tri-dimensional filter method can make full use of the information we get along the algorithm process.

This paper is divided into 4 sections. The next section introduces the concept of a Modified tri-dimensional filter and the NCP function. In Section 3, an algorithm of line search filter is given. The global convergence properties are proved in the last section.

2. Preliminaries

2.1. NCP Function

The method that based on the Fischer-Burmeister NCP function are efficient, both theoretical results and computational experience. The Fischer-Burmeister function has a very simple structure

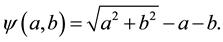
We know that: is continuously differentiable everywhere except at the origin, but it is strongly semismooth at the origin. i.e. if 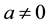or, then is continuously differentiable at, and

if and, then the generalized Jacobian of at is

Let

We denote, where

Clearly, the KKT optimality conditions (2) can be equivalently reformulated as the nonsmooth equations.

If, then is continuously differentiable at. In this case, we have

where is the ith column of the unit matrix, its ith element is 1, and other elements are 0.

If, then is strongly semismooth and directionally differentiable at. We have

and

We may reformulated the KKT (at point) conditions as a system of equations.

where and are the multiplier vectors,

.

Replace the violation constrained function in filter F of Fletcher and Leyffer method, we use the

violation constrained function.

If, let

otherwise we denote

Let

where H^k is a positive matrix which may be modified by BFGS update. or denotes the diagonal matrix whose j diagonal element is or respectively.

Definition 1.1 [1] A pair is said to dominate another pair if and only if both and.

Definition 1.2 [1] A filter is a list of pairs such that no pair dominates any other. A point is said to be acceptable for inclusion in the filter if it is not dominated by any point in the filter.

Definition 1.3 NCP pair and NCP functions [6] We call a pair to be an NCP pair if, and a function is called an NCP function if if and only if is an NCP pair.

Denote in the following context. It is straightforward to see that the constraint (1) is equivalent to the following equation:.

2.2. Tri-Dimensional Filter

A two dimensional filter is often used in traditional filter method, some information about convergent like the positions of iterates are neglected. Therefore, we aim to enhance its flexibility of filter. Motivated by [5] , we adopt in which a parameter is used to relax the criterion of iterates. We denote the filter by for each iteration k. Flexible exact penalty function is introduced to promote convergence refer to [7] . Given a prescribed interval, penalty parameter can be chosen as any number from it and it is extends classical penalty function methods. We generalized the idea to filter which we called Tri-dimensional filter. Different from the original two dimensional filter, we increase a dimension by introducing a parameter.

We use pairs to constitute the elements of filter, where is a non-negative parameter. Our strategy for setting depends on the region in space to which moves into. Figure 1 is Distinct regions defined by the current iterate.

If moves into region I, which is defined as

We say that the algorithm does not make good improvement since we do not want to accept points with larger constraint violation. Thus, we try to impose stricter acceptance criterion. Meanwhile, we do not permit larger than. In our algorithm, we increase in the following way

(3)

If s_k moved into region P which is defined as

We say that the algorithm makes good improvement since it reduces not only the constraint violation, but also the penalty function value. So, we may loosen the acceptance criterion to wish more improvement. Here, we achieve this goal by reducing by setting

4)

In our algorithm, the trial step s_k is accepted by filter if

(5)

For all. The parameter is a constant close to 1 which sets an “envelope” around the border of the dominated part of the -space in which the trial step is rejected. And also in the filter if

(6)

then we say is dominated by.

3. Description of the Algorithm

In this section we hope that the Lagrange multiplier will converge to the Lagrange multiplier at the solution. From the KKT system of (1), a good estimate of the Lagrange multiplier is the least square solution of, namely. In our algorithm, is updated only after a trial step is accepted, and is set componentwise as

(7)

Now, we consider how to update the penalty parameter. Let be a solution of (1) at which the LICQ is

satisfied, and the second order sufficient conditions are satisfied. Then when is the strict local

minimizer of penalty function. So we force the condition at each iteration:.

And also, since the penalty term aims to reduce the constraint violation we double the penalty parameter if the constraint violation could not reduce by half, that is

To summarize, we update the penalty parameter in the following formula:

(8)

The improved algorithm is presented as following.

Algorithm

Step 0. Initialization: Give a starting point, , and a initial positive definite matrix, ,. compute.

Step 1. Terimination test. If then returing x_k as a solution and stop.

Step 2. Computation of the search direction. compute and by solving the following linear system in:

(9)

where.

If, then stop otherwise, compute by solving the following linear system in:

(10)

where and.

Step3. Liner search with filter

If then let and, otherwise if then let and, otherwise de- note and

(11)

and let

Step 4. Acceptance criterion of the trial step

Let, evalute; If is accepted by filter, and go to step 5;, and; go to step 2.

Step 5. Paramenters update

Update by (7); Update by (8); Update by (3) or (4); go to step 1.

4. The Convergence Properties

To present a proof of global convergence of algorithm, in this section, we always assume that the following conditions hold.

A1 The level set is bounded, and for sufficiently large k,

A2 are twice Lipschitz continuously differentiable, and for all

where is the Lipschitz constant.

A3 is positive definite and there exist positive numbers and such that

for all and all.

Lemma 1. If then and are nonsingular.

Proof. If for some, where, then we have

(12)

and

(13)

From the definition of and, we know that and for all j. So, diag is nonsingular. We have

(14)

Putting (14) into (12), we have

The fact that is positive semidefinite implies, and then by

(14). is nonsingular. And if is an accumulation point of, , and. If then is nonsingular. This lemma holds.

The lemma 2 hold (see [8] Lemma 2)

Lemma 2. If, then. and is KKT point of problem (NLP).

Lemma 3. Consider an infinite sequence iterations on which entered into filter, where

and is bounded below. It follows that.

Proof. Suppose the theorem is not true, then exists an and an infinitely members of index set K such that either and for any. then we obtain that, or is monotonically decreasing, then lemma 5.1 implies. So, the lemma holds.

The following lemma 4 - 5 hold (see [9] )

Lemma 4.

Lemma 5. If is an accumulation point of then, and is the solution of:

and.

Theorem 1. If is an accumulation point of then is a KKT point of Problem (NLP).

It is obviously to prove the conclusion holds according to the above lemmas.

Acknowledgements

We thank the Editor and the referee for their comments. This work is supported by the National Natural Science Foundation of China (No. 11101115), the Natural Science Foundation of Hebei Province (No. 2014201033) and the Science and Technology project of Hebei province (No. 13214715).

References