Received 21 November 2014; accepted 19 June 2015; published 23 June 2015

ABSTRACT

In this paper, an approximate analytical method to solve the non-linear differential equations in an immobilized enzyme film is presented. Analytical expressions for concentrations of substrate and product have been derived for all values of dimensionless parameter. Dimensionless numbers that can be used to study the effects of enzyme loading, enzymatic gel thickness, and oxidation/ reduction kinetics at the electrode in biosensor/biofuel cell performance were identified. Using the dimensionless numbers identified in this paper, and the plots representing the effects of these dimensionless numbers on concentrations and current in biosensor/biofuel cell are discussed. Analytical results are compared with simulation results and satisfactory agreement is noted.

Keywords:

Michaelis-Menten Kinetics, Biofuel and Biosensor, Homotopy Perturbation Method, Immobilized Enzyme Systems

1. Introduction

Biosensors and biofuel cells are commonly used for industrial, environmental and medical applications. However there are no clear guidelines for the design of electrochemical biosensors or biofuel cells employing immobilized enzymes that will produce a targeted linear range, limit of detection and sensitivity. Such guidelines can be provided using analytical simulation tools that assess sensor feasibility prior to extensive development.

Biosensors and biofuel cell face increasing demand for selective and sensitive detection of different molecules for industrial, environmental and clinical applications [1] -[4] . There are many affordable alternatives to laboratory techniques that require trained personnel, expensive equipment and possibly delayed response time. Electrochemical biosensors and biofuel cell especially desirable for use in field applications because of their compact design, ease of manufacture, real time response, sensitivity and selectivity [3] -[6] . They are used in many applications ranging from glucose detection to detection of neurotoxic agents [1] [6] [7] . Here we focus on biosensors and biofuel cell that employ immobilized enzymes and the electrochemical detection of the enzymatic reaction. Some important parameters that affect these goals are listed and include transport of the substrate and the product through the immobilized enzyme layer, oxidation/reduction kinetics at the electrode, enzyme activity and loading and operating conditions such as pH and temperature. Of these parameters optimizing the enzyme loading and activity has been a major challenge and it depends primarily on the enzyme immobilization method. Different methods such as chemical modification of the electrode surface, entrapment in a membrane and physical absorption are commonly used to create enzyme layers on electrodes [8] .

A mathematical model considering reaction and diffusion processes in biofuel cell or biosensor, contains a system of non-linear partial differential equations. Numerical and analytical solutions to the reaction-diffusion equations have been presented for different cases by many authors [9] -[14] . Analytical solutions are available for limiting cases, whereas numerical solutions were used to determine and optimize a wide range of experimental parameters [15] . Many of the earlier studies have focused on optimizing glucose biosensors where the enzyme was entrapped in a redox hydrogel [16] [17] . Simple Michaelis-Menten kinetics was used to model the enzyme kinetics, and first order kinetics between the mediator and the electrode were assumed [9] [17] . The effects of experimental parameters on the response at steady state and during a transient were studied [12] . Especially the behavior of the glucose sensor in the diffusion limited regime was analyzed since this leads to an extended linear range [16] [18] . Substrate and product inhibition in an enzyme with first order reaction kinetics [19] , diffusion through a semi-permeable outer membrane [20] [21] and data analysis to determine kinetic constants and enzyme activity [22] were also studied by different groups.

Sachin [23] used a finite difference method for electrochemical biosensors with an immobilized enzyme layer. Sachin described the general criteria using Michaelis-Menten rate equation and effect of gel thickness on the response of this biosensor. To our knowledge no rigorous analytical solutions for non-steady-state concentration and current have been reported. In this paper, we have derived the analytical expressions of concentration and current using a new approach of Homotopy perturbation method [24] -[27] . The result of the Equations (2)-(3) in immobilized enzyme system is relevant because its solution describes important applications such as biosensors, bioreactors, and biofuel cells, among others.

2. Mathematical Formulation of the Problem

The chemical reactions in the layer are

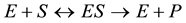(1)

where E refers to the enzyme, S is the substrate, ES is a transitory complex assumed to be at a steady concentration, and P is the product. The schematic of the system modeled in this study is shown in Figure 1. An aqueous drop containing substrate (S) is placed on the electrode with an immobilized enzyme layer. As the substrate diffuses through the enzyme layer it reacts with the enzyme to form the product (P). The product then diffuses through the layer, and if it is electroactive, is oxidized or reduced at the electrode. When modeling this system, we used Michaelis-Menten equation to describe the kinetics within the enzyme layer and coupled it with Fick’s law to describe the diffusion of the substrate and product as shown in Equations (2)-(3):

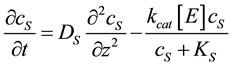(2)

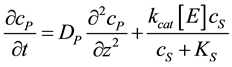(3)

where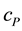, , 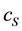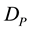and represent the concentrations and diffusion coefficients of the product and the substrate, respectively. 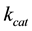is the catalytic rate constant in the Michaelis-Menten mechanism, [E] is enzyme loading, and 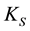is Michaelis constant for the substrate. In the above equations the initial and boundary conditions are given by

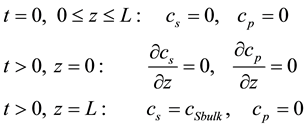(4)

where z is the distance from the electrode surface and L is the enzyme layer thickness.

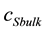represents the concentration of substrate in bulk solution. Current i occurring at the electrode surface due to reduction or oxidation of P is given by

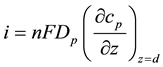(5)

Equations (2)-(3) were made dimensionless using the following dimensionless parameters:

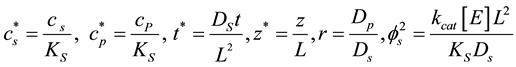(6)

The Equations (2)-(3) in dimensionless form becomes as follows:

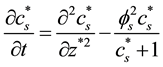(7)

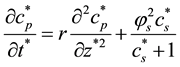(8)

From the Equation (4), the initial and boundary conditions in dimensionless form are given by

(9)

Dimensionless current density becomes

(10)

3. General Analytical Expression of Concentration of Substrate and Product under Non-Steady State Condition Using Homotopy Perturbation Method (HPM)

In recent days, HPM is often employed to solve several analytical problems. In addition, several groups demonstrated the efficiency and suitability of the HPM for solving nonlinear equations in electrochemical problems [28] -[31] . He et al. [24] , used HPM to solve the Lighthill equation, the Duffing equation [25] and the Blasius equation [26] . HPM has also been used to solve non-linear boundary value problems [27] , integral equation [32] -[34] , Klein-Gordon and Sine-Gordon equations [35] , Emden-Flower type equations [36] and several other problems. Laplace transform and Homotopy perturbation method are used to solve the non-linear differential Equations (7)-(8) (Appendix A). The analytical expressions of non-steady state concentrations are as follows:

(11)

(12)

where, (13)

Using (10) and (12), the current is given by

(14)

When (steady state), the above equation becomes

(15)

4. Discussion

Equations (11) (12) and (14) are the new and simple analytical expressions of concentrations of substrate, product and current respectively. To show the efficiency of our non-steady-state result, it is compared with numerical solution in Figure 2 & Figure 3. Satisfactory agreement is noted. The SCILAB/MATLAB program is also given in Appendix B. Figure 2 shows the time-dependent normalized concentration profiles for the substrate in the enzyme membrane. Figures 2(a)-(c) show dimensionless concentration versus the dimensionless

distance. The concentration of substrate depends upon the dimensionless parameter “a”. The dimensionless parameter “a” depends upon and. When Thiele modulus is small, the kinetics dominate and the uptake of the substrate are kinetically controlled. From Figure 2(a), it is evident that the value of the substrate concentration decreases when the Thiele modulus increases or Figure 2(b) illustrates that, when t increases, the concentration of the substrate decreases. It is obvious from Figure 2(c) that when initial substrate concentration increases, the concentration of substrate also decreases.

The normalized concentration of the product for various values of Thiele modulus, time t and ratio of diffusion coefficient is plotted in Figures 3(a)-(c). From the Figure 3(a) & Figure 3(b), it is inferred that the normalized concentration product increases with the decrease in the value of and time t. The product concentration is increases when the ratio of diffusion coefficient decreases as shown in Figure 3(c).

The value of current i increases slightly when the Thiele modulus increases or electrode thickness increases as shown in Figure 4(a). From Figure 4(b), it is inferred that the ratio of diffusion coefficient r increases the current density is decreases. The current density increases as initial substrate concentration

decreases.

5. Estimation of Kinetic Parameters

The current is dependent upon the parameters Thiele module and initial substrate concentration. When, (or) Equation (15) can be written as

(16)

Substituting the value of and in the above equation, we get

(17)

The plot of versus gives the slope and intercept

as shown in Figure 5. From these plots, we can obtain the value of kinetic parameters.

6. Conclusion

The theoretical behavior of biofuel cell/biosensor was analyzed. The coupled time dependent non-steady state non-linear diffusion equations in biosensor or biofuel cell have been solved analytically and numerically. These analytical results will be used in determining the kinetic characteristics of the biofuel cell or biosensor. The analytical expressions for substrate, product concentration and transient current response are obtained using the method of Laplace transformation and HPM. A good agreement with numerical simulation data is noticed. Concentration of substrate, product and current depends upon Thiele modulus and initial concentration of substrate which is discussed in this communication. Evaluation of kinetic parametr from the response of the steady-state current is also completely discussed. The theoretical model presented here can be used for the optimization of the design of the biosensor.

Acknowledgements

This work is supported by the Department of Science and Technology (DST) (No. SB/SI/PC-50/2012), Government of India. The authors are thankful to Shri. S. Natanagopal, Secretary, The Madura College Board and Dr. R. Murali, Principal, Mr. S. Muthukumar, Head of the Department, Department of Mathematics, The Madura College (Autonomous), Madurai, Tamilnadu, India for their constant encouragement.

References

Nomenclature

Appendix A

Solution of Equations (7) and (8) Using Complex Inversion Formula

In this appendix we indicate how Equations (11) and (12) are derived, by solving a differential equation of second order with constant coefficients by using new homotopy approach and Laplace transform in Equations (7) and (8), and the boundary conditions. The obtained solution of the Equation (7) as

(A1)

In this appendix we indicate how Equation (A1) may be inverted using the complex inversion formula. If represents the Laplace transform of a function, then according to the complex inversion formula we can state that

(A2)

where the integration in Equation (A2) is to be performed along a line in the complex plane where. The real number is chosen such that lies to the right of all the singularities, but is otherwise assumed to be arbitrary. In practice, the integral is evaluated by considering the contour integral presented on the right-hand side of Equation (A2), which is then evaluated using the so-called Bromwich contour. The contour integral is then evaluated using the residue theorem which states for any analytic function

(A3)

where the residues are computed at the poles of the function. Hence from Equation (A3), we note that

(A4)

From the theory of complex variables we can show that the residue of a function at a simple pole at is given by

(A5)

Hence in order to invert Equation (A1), we need to evaluate

The poles are obtained from. Hence there is a simple pole at and there are infinitely many poles given by the solution of the equation and

so where

Hence we note that

(A6)

The first residue in Equation (A6) is given by

(A7)

The second residue in Equation (A6) is given by

(A8)

where is defined as in Equation (13). Here we used and. From (A6), (A7) and (A8) we conclude that

(A9)

Similarly we can invert Equation (8) by using complex inversion formula.

Appendix B

Scilab/Matlab Program to Find the Numerical Solution of Equations (7) and (8)

function see5

m =0;

x =linspace(0,1);

t=linspace(0,5);

sol=pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);

u1 = sol(:,:,1);

u2 = sol(:,:,2);

%figure

%plot(x,u1(end,:))

%title('u1(x,t)')

%xlabel('Distance x')

%ylabel('time ')

%------------------------------------------------------------------

figure

plot(x,u2(end,:))

title('u2(x,t)')

xlabel('Distance x')

ylabel('u2(x,2)')

%------------------------------------------------------------------

function [c,f,s] = pdex4pde(x,t,u,DuDx)

r=1;

c =[1;r];

f =[1;1].*DuDx;

e =0.5;

F=(e^2)*u(1)/(1+u(1));

s=[-F,F];

% --------------------------------------------------------------

function u0 = pdex4ic(x)

u0 =[0;0];

% --------------------------------------------------------------

function [pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t)

pl = [0;0];

ql = [1;1];

pr = [ur(1)-1;ur(2)-0];

qr = [0;0];