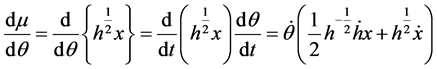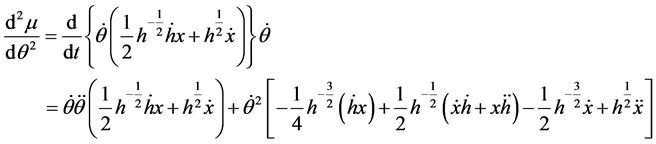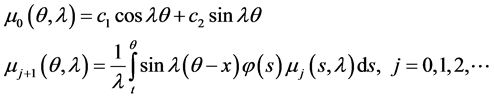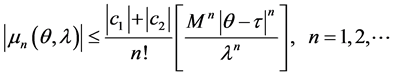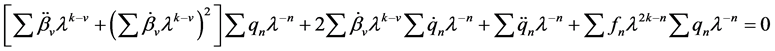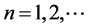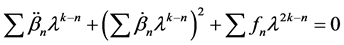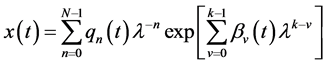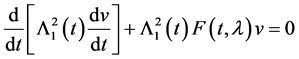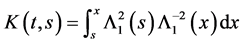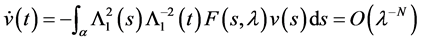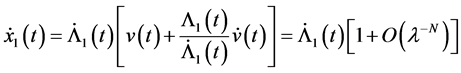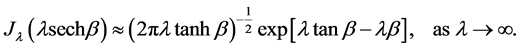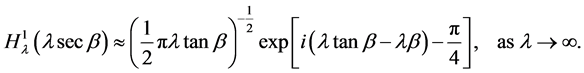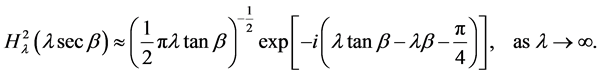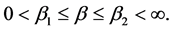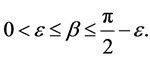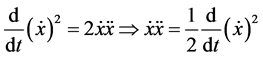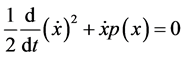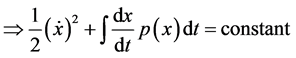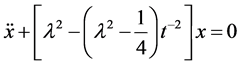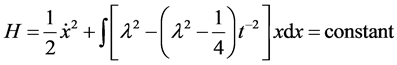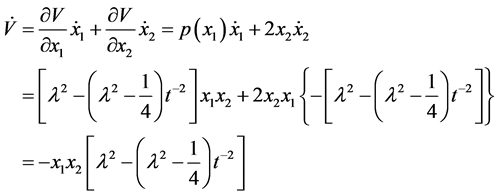Applied Mathematics
Vol.07 No.03(2016), Article ID:63808,10 pages
10.4236/am.2016.73018
A Note on Differential Equation with a Large Parameter
S. O. Maliki, R. N. Okereke
Department of Mathematics Michael Okpara, University of Agriculture, Umudike, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 October 2015; accepted 22 February 2016; published 25 February 2016
ABSTRACT
We present here asymptotic solutions of equations of the type , where
, where 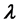 is a large parameter. The Bessel differential equation
is a large parameter. The Bessel differential equation 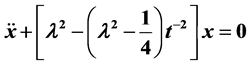 is considered as a typical example of the above and the solutions are provided as
is considered as a typical example of the above and the solutions are provided as . Furthermore, the behaviour of the solutions as well as the stability of the Bessel ode is investigated numerically as the parameter grows indefinitely.
. Furthermore, the behaviour of the solutions as well as the stability of the Bessel ode is investigated numerically as the parameter grows indefinitely.
Keywords:
ODE, Asymptotic Solutions, Bessel Differential Equation, Stability, MathCAD Solution

1. Introduction
The theory of ordinary homogeneous linear differential equations of the second order, containing a large parameter, is well established [1] - [4] . The aim of this paper is to investigate detailed analytical solutions of equations of the form;
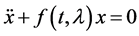 (1.1)
(1.1)
where  is
is  and
and 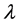 is a real parameter. We shall investigate the behaviour of solutions of this differential equation, and the stability of the origin as
is a real parameter. We shall investigate the behaviour of solutions of this differential equation, and the stability of the origin as . Without loss of generality, we take
. Without loss of generality, we take 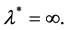 First, we make the following remarks:
First, we make the following remarks:
a) Any second order linear ODE of the form; 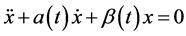 can be reduced to
can be reduced to 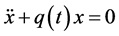 by a suitable transformation.
by a suitable transformation.
b) Furthermore, any equation of the form 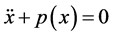 is conservative. We shall demonstrate this shortly. This will help us in our asymptotic stability analysis.
is conservative. We shall demonstrate this shortly. This will help us in our asymptotic stability analysis.
c) In Equation (1.1) if we take;  then, we have the well known Sturm-Liouville problem;
then, we have the well known Sturm-Liouville problem;
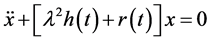 (1.2)
(1.2)
where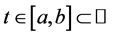
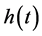
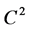
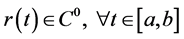
Introducing the new variables;

If we suppress the variable t for the moment, it then follows that;
Therefore
Since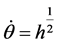
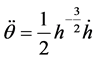
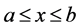
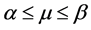
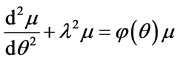
where
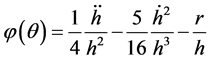
is a continuous function of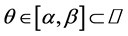
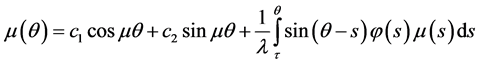
where 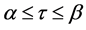
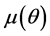
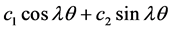
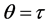
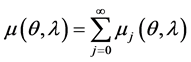
where;
Assuming that the function 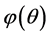
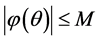
In the case of a finite interval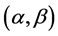
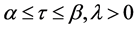
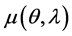
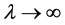

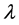
2. Formal Solutions
Let us now consider the general ode;

If 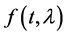

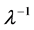
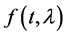

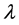
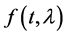
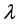

In (2.1), we shall assume that 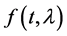
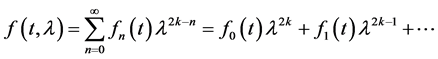
where the 
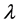
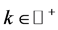
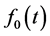

Substituting (2.3) into (2.1), with the convention that 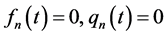
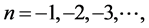
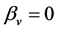
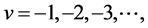
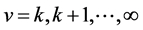
Picking out the coefficients of 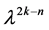
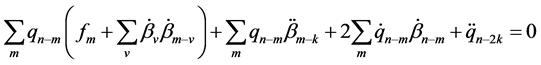
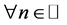
This first condition arises when 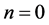
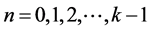
It then follows that;
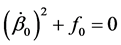

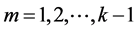
Consequent upon these relations, we may restrict our summation to 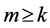
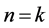
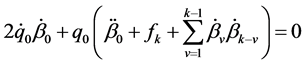
and when we replace n by 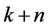
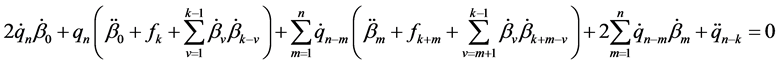
It is now obvious that Equation (2.3) satisfies (2.1), provided that 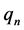
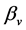
In these equations, empty sums (i.e. those with upper limit
we may choose a branch of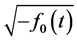
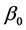

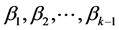
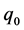

stant multiple of 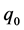
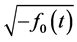
3. Another Formal Solution
A second type of formal solution is given by
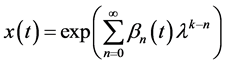
Substituting (2.9) into (2.1) we get;
Equating coefficients of
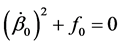
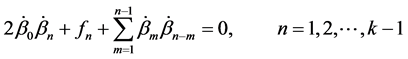
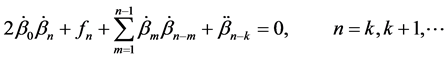
There are two linearly independent formal solutions of this type. The obvious connection between these two types of formal solutions can be seen from the fact that equations (2.10) and (2.11) are identical with (2.5) and
(2.6), and 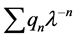
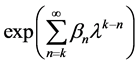
3.1. Remark
In the foregoing, we have assumed that 
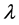

3.2. Asymptotic Solutions
We shall now demonstrate that under certain assumptions, the differential Equation (2.1) possesses a fundamental system of solutions which are represented asymptotically by the formal solutions obtained in preceding section. It actually does not matter whether we compare solution of (2.1) with
where the 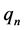

where the 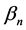
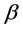
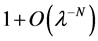
We now fix a positive integer N, and set;
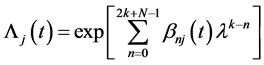
with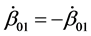


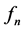
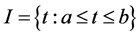
3.3. Theorem
Let S and I be as defined above then for each fixed 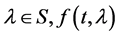
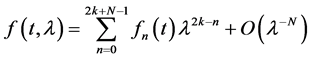
Uniformly in t and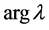
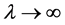
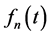

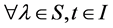
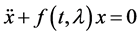
possesses a fundamental system of solutions, 
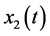
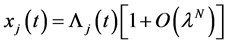
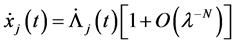
Proof
Top establish the existence and asymptotic property of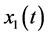
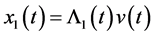
in Equation (3.4) to get
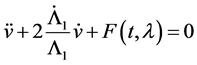
where
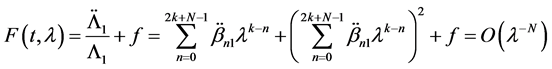
uniformly in t and 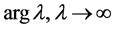
By two successive integrations, and a suitable choice of the constants of integration, we obtain;

where
Since 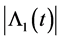
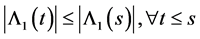
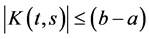
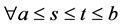
The existence of 
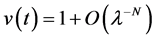
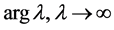
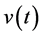
and
This proves (3.5) for
4. Application
The methods of the last two sections can be applied to prove the asymptotic formulae for the Bessel functions [1] , viz;
1)
2)
3)
Equation (1) holds for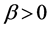
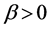
Equations (2) and (3) hold for 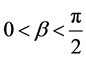

We observe that the functions; 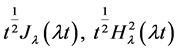
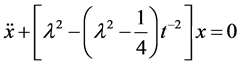
This equation is of the form (3.4) with 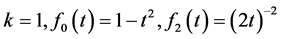

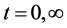

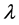
5. Stability Analysis
In Section 1.0, we claimed that any equation of the form 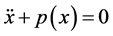
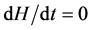
Let us begin by multiplying the equation 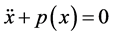
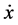
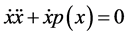
Observing that
Hence (3.11) becomes
Thus, the required Hamiltonian is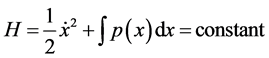
The Bessel differential equation
can be recast in vector form as
Clearly the origin (0, 0) is the only critical point and the corresponding Hamiltonian is;
We use the above Hamiltonian to construct a Lyapunov function given by;
with 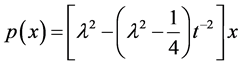
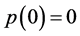

Thus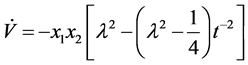
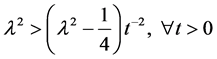
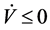
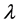
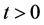
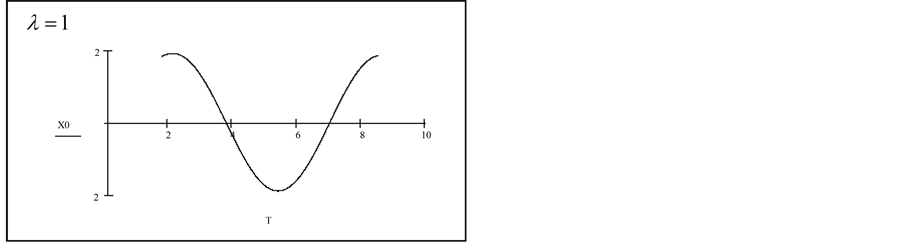
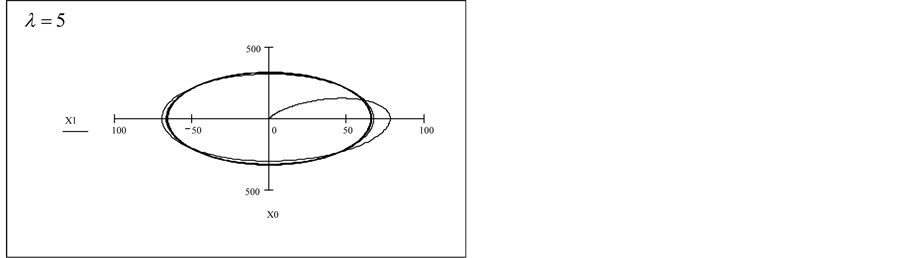
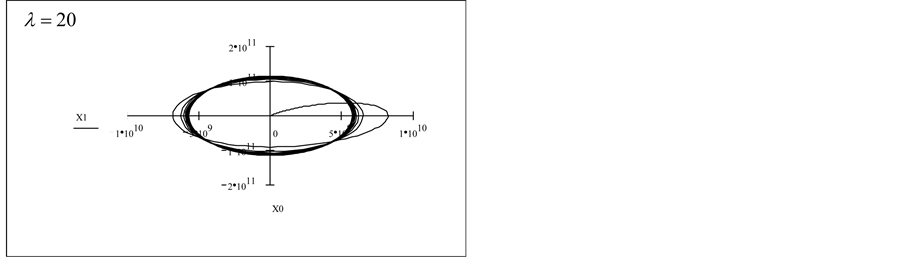
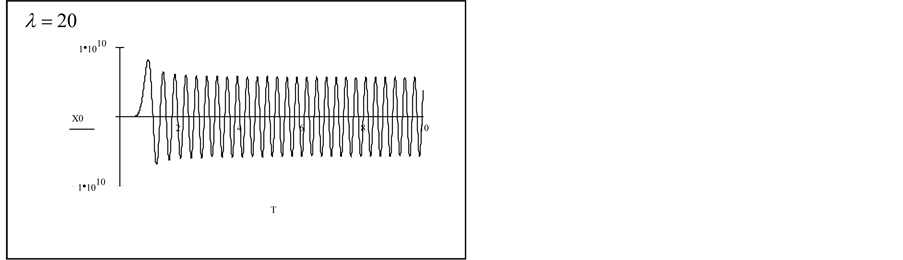
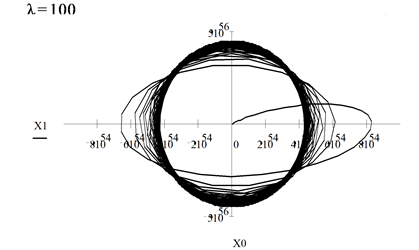
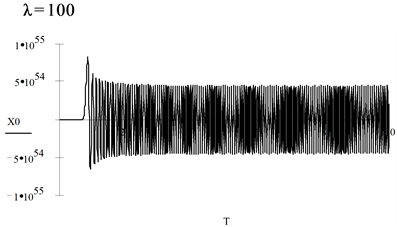
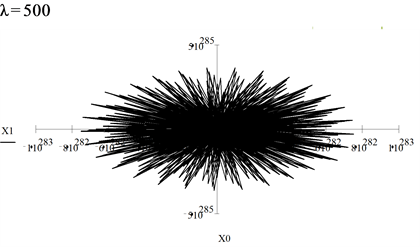
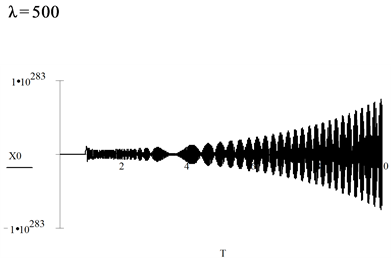
6. Numerical Investigation of Asymptotic Solutions
In what follows, we employ the Runge-Kutta algorithm provided by MathCAD [5] software to obtain a numerical solution for large values of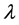
6.1. MathCAD Runge-Kutta Algorithm
We define the following for the MathCAD algorithm.
t0: = 0.2 t1: = 10 Solution interval endpoint
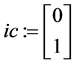
N: = 1500 Number of solution values on [t0, t1]
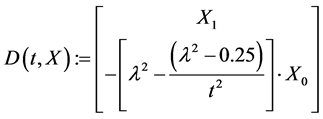
S: = rkfixed (ic, t0, t1, N, D) Runge-Kutta algorithm.
T: = S<0> Independent variable values.
X0: = S<1> First solution function values.
X1: = S<2> Second solution function values.
Remark: X0 represents solution values x satisfying the Bessel ODE, while X1 represents the derivative of X0 i.e.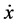
6.2. Simulations
Figure 1. Section of solution matrix S.
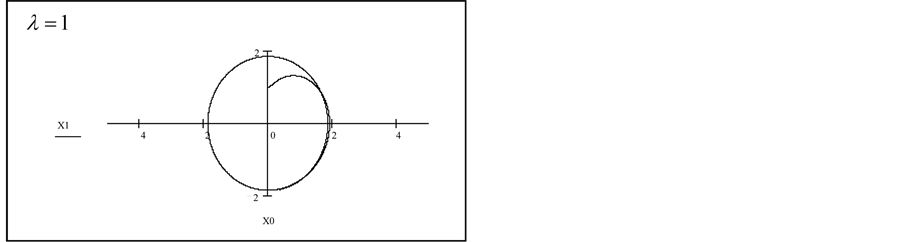
6.3. Observations
For 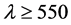
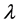


6.4. Conclusion
In this work, we have studied asymptotic solutions of equations of the type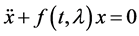

Bessel differential equation 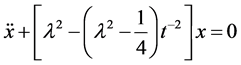
the stability of the origin is investigated numerically as the parameter grows indefinitely.
Cite this paper
S. O. Maliki,R. N. Okereke, (2016) A Note on Differential Equation with a Large Parameter. Applied Mathematics,07,183-192. doi: 10.4236/am.2016.73018
References
- 1. Olver, F.W.J. (1997) Asymptotics and Special Functions. Academic Press, New York. Reprinted by AK Peters, Wellesley.
- 2. Shkil, M.I. (1971) Asymptotic Methods in Differential Equations. Vyshcha Shkola, Kyiv, 228 p.
- 3. Territin, Kh.L. (1957) Asymptotic Expansion of Solutions to System of Ordinary Differential Equations Containing Parameter. Matematika: Sb. per., 1, 29-59.
- 4. Tikhonov, A. (1948) On Dependence of Solutions of Differential Equations on Small Parameter. Mat. Sb., 28, 193-204.
- 5. MathSoft, Inc. (1997) MathCAD 7 User’s Guide.
http://www.mathsoft.com