Applied Mathematics
Vol.05 No.20(2014), Article ID:51586,6 pages
10.4236/am.2014.520304
Symmetry Reduction and Explicit Solutions of the (2 + 1)-Dimensional DLW Equation
Zhengyi Ma1,2, Jinxi Fei1, Yuanming Chen1
1Department of Mathematics, Zhejiang Lishui University, Lishui, China
2Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai, China
Email: ma-zhengyi@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 August 2014; revised 25 September 2014; accepted 18 October 2014
ABSTRACT
Utilizing the Clarkson-Kruskal direct method, the symmetry of the (2 + 1)-dimensional dispersive long wave equation is derived. From which, through solving the characteristic equations, four types of the explicit reduction solutions that related the hyperbolic tangent function are obtained. Finally, several soliton excitations are depicted from one of the solutions.
Keywords:
dispersive long Wave Equation, symmetry Reduction, Explicit solution,soliton Excitation

1. Introduction
Soliton theory, one of the typical topics in nonlinear science, has been widely applied in optics of nonlinear media, photonics, plasmas, mean-field theory of Bose-Einstein condensates, condensed matter physics, and many other fields. For describing these nonlinear physical phenomena, the study of symmetry is a very important approach, especially in the integrable nonlinear partial differential equations (NPDEs) for the sake of the existence of symmetries in infinity. Traditionally, there are three powerful methods to find the symmetry structure of the NPDEs, that is, the Lie group method of infinitesimal transformations, the nonclassical Lie group method and the Clarkson and Kruskal (CK) direct method [1] - [5] . Among them, the classical Lie symmetries of the partial differential equations (PDEs) can be obtained through the Lie group method of infinitesimal transformations. Using the basic prolongation method and the infinitesimal criterion of invariance, one can find some particular Lie point symmetries group of the NPDEs.
In Section 2 of this paper, a (2 + 1)-dimensional dispersive long wave (DLW) equation is taken to illustrate the symmetry reduction related the CK direct method. Section 3 is a direct result which the explicit reduction solutions are solved and the soliton excitations are depicted. Section 4 is the conclusion.
2. Symmetry Structure through the Direct Approach
In the following of this paper, we fucus on the (2 + 1)-dimensional dispersive long wave (DLW) equation
 (1)
(1)
The system was first derived by Boiti et al. as a compatibility for a weak Lax pair [6] . In Ref. [7] , Paquin and Winternitz showed that the symmetry algebra of Equation (1) is infinite-dimensional and a Kac-Moody-Virasoro structure. The more general symmetry algebra,  symmetry algebra, was given in Ref. [8] . In Ref. [9] , Lou gave out nine types of two dimensional similarity reductions and thirteen types of ordinary differential equation reductions. In Ref. [10] , Lou showed that Equation (1) has no Painléve property, though the system is Lax or 1ST integrable. Abundant propagating localized excitations were also derived by Lou [11] [12] with the help of Painlvé-Bäcklund transformation and a multilinear variable separation approach. With the aid of a projective Riccati equation approach and by introducing appropriate lower-dimensional localized patterns, abundant coherent soliton excitations, that is, solitons, chaos and fractals were derived by ours [13] - [15] .
symmetry algebra, was given in Ref. [8] . In Ref. [9] , Lou gave out nine types of two dimensional similarity reductions and thirteen types of ordinary differential equation reductions. In Ref. [10] , Lou showed that Equation (1) has no Painléve property, though the system is Lax or 1ST integrable. Abundant propagating localized excitations were also derived by Lou [11] [12] with the help of Painlvé-Bäcklund transformation and a multilinear variable separation approach. With the aid of a projective Riccati equation approach and by introducing appropriate lower-dimensional localized patterns, abundant coherent soliton excitations, that is, solitons, chaos and fractals were derived by ours [13] - [15] .
According to the Clarkson and Kruskal (CK) direct method [4] [5] , we first seek the similarity reduction of Equation (1) in the form of
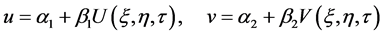 (2)
(2)
where ,
, 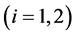
 and
and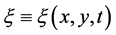 ,
,  ,
, 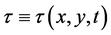 are all
are all
differentiable functions to be determined, 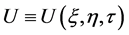 ,
, 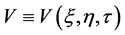 satisfy the following DLW equation
satisfy the following DLW equation
as Equation (1)
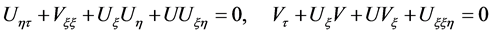 (3)
(3)
The result of the symbolic computation, one can deduce
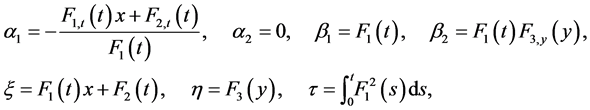 (4)
(4)
where 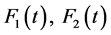 and
and  are arbitrary functions of their own variables.
are arbitrary functions of their own variables.
Utilizing the variable separation solution of Equation (3) which derived in Refs. [13] [14]
 (5)
(5)
the similarity solution of Equation (1) can be written

where 



Second, under the transformation

with the infinitesimal parameter


then Equation (2) can reduce to



The equivalent vector expression of the above symmetry is

When taking

from Equation (13), the following six operators are obtained

Hence, we obtain the commutator table listed in Table 1 with the 
according to the commutator operators
3. Reduction Solutions
Solving the following characteristic equations

with




1) Taking 

where
2) Taking 
Table 1. Lie Bracket.

where
3) Taking 
Equations (16)

4) Taking 

As we all know, to derive soliton structures of a explicit solution is a meaningful task fo a nonlinear physical
equation. Now, when taking 

dromion-like structure, is found if the constants







The solitoff is another special type of coherernt structure for a nonlinear equation, where the wave fields
decays exponentially in all directions except for a preferred direction [16] . For the field
structure can also be constructed. Figure 2(a) shows a two-solitoff solution when taking the constants






Figure 1. (a) A dromion structure of the solution (17) when taking the constants 





Figure 2. (a) A two-solitoff soliton of the solution (17) when taking the constants




function

solitons is depicted (Figure 2(b)).
4. Summary and Conclusion
In summary, we have obtained the symmetry reduction with the aid of the CK direct method and some explicit solutions through solving the characteristic equations of the (2 + 1)-dimensional DLW equation. These obtained solutions contain several free functions of variables 

Acknowledgements
The authors are grateful to Profs Lou S. Y. and Chen Y. and Drs Xin X. P. and Hu X. X. for their helpful suggestions and fruitful discussion.
Funding
Supported by the Natural Science Foundation of Zhejiang Province, China under Grant Nos. LY14A010005 and LQ13A010013.
Cite this paper
Zhengyi Ma,Jinxi Fei,Yuanming Chen, (2014) Symmetry Reduction and Explicit Solutions of the (2 + 1)-Dimensional DLW Equation. Applied Mathematics,05,3264-3269. doi: 10.4236/am.2014.520304
References
- 1. Bluman, G.W. and Cole, J.D. (1974) Similarity Methods for Differential Equations. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-1-4612-6394-4 - 2. Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-1-4757-4307-4 - 3. Olver, P.J. (1993) Applications of Lie Groups to Differential Equations. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-4350-2 - 4. Clarkson, P.A. and Kruskal, M.D. (1989) New Similarity Reductions of the Boussinesq Equation. Journal of Mathematical Physics, 30, 2201-2213.
http://dx.doi.org/10.1063/1.528613 - 5. Clarkson, P.A. and Mansfield, E.L. (1994) Algorithms for the Nonclassical Method of Symmetry Reductions. SIAM Journal on Applied Mathematics, 54, 1693-1719.
http://dx.doi.org/10.1137/S0036139993251846 - 6. Boiti, M., Leon, J.J.P. and Pempinelli, F. (1987) Integrable Two-Dimensional Generalisation of the Sine and Sinh- Gordon Equations. Inverse Problems, 3, 37-50.
http://dx.doi.org/10.1088/0266-5611/3/1/009 - 7. Paquin, G. and Winternitz, P. (1990) Group Theoretical Analysis of Dispersive Long Wave Equations in Two Space Dimensions. Physica D, 46, 122-138.
http://dx.doi.org/10.1016/0167-2789(90)90115-6 - 8. Lou, S.Y. (1994) Symmetries and Algebras of the Integrable Dispersive Long Wave Equations in 2+1-Dimensional Spaces. Journal of Physics A: Mathematical and General, 27, 3235-3243.
http://dx.doi.org/10.1088/0305-4470/27/9/033 - 9. Lou, S.Y. (1995) Similarity Solutions of Dispersive Long Wave Equations in Two Space Dimensions. Mathematical Methods in the Applied Sciences, 18, 789-802.
http://dx.doi.org/10.1002/mma.1670181004 - 10. Lou, S.Y. (1993) Painlevé Test for the Integrable Dispersive Long Wave Equations in Two Space Dimensions. Physics Letters A, 176, 96-100.
http://dx.doi.org/10.1016/0375-9601(93)90322-Q - 11. Tang, X.Y. and Lou, S.Y. (2003) Extended Multilinear Variable Separation Approach and Multivalued Localized Excitations for Some (2 + 1)-Dimensional Integrable Systems. Journal of Mathematical Physics, 44, 4000-4025.
http://dx.doi.org/10.1063/1.1598619 - 12. Tang, X.Y., Lou, S.Y. and Zhang, Y. (2002) Localized Exicitations in (2 + 1)-Dimensional Systems. Physical Review E, 66, Article ID: 046601.
http://dx.doi.org/10.1103/PhysRevE.66.046601 - 13. Ma, Z.Y., Liu, Y.L., Lu, Z.M. and Zheng, C.L. (2006) Solitons and Waves in (2 + 1)-Dimensional Dispersive Long-Wave Equation. Communications in Theoretical Physics, 46, 799-803.
http://dx.doi.org/10.1088/0253-6102/46/5/006 - 14. Ma, Z.Y. and Hu, Y.H. (2007) Solitons, Chaos and Fractals in the (2 + 1)-Dimensional Dispersive Long Wave Equation. Chaos, Solitons & Fractals, 34, 1667-1676.
http://dx.doi.org/10.1016/j.chaos.2006.04.073 - 15. Ma, Z.Y. (2007) The Projective Riccati Equation Expansion Method and Variable Separation Solutions for the Nonlinear Physical Differential Equation in Physics. Chinese Physics B, 16, 1848-1854.
http://dx.doi.org/10.1088/1009-1963/16/7/007 - 16. Ruan, H.Y. (2001) Study of Solitons Interaction in Integrable Models. Acta Physica Sinica, 50, 369-376.




