Received 4 September 2014; revised 26 September 2014; accepted 6 October 2014

ABSTRACT

Let G be a locally compact group, H a closed amenable subgroup and u an element of the Herz Figà-Talamanca algebra of H with compact support, we prove the existence of an extension of u to G, with a good control of the norm and of the support of the extension.

Keywords:

Convolution Operators, Locally Compact Groups, Abstract Harmonic Analysis, Amenable Groups

1. Introduction

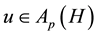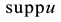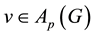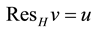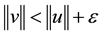Let G be a locally compact group and H a closed subgroup, this paper is concerned with the problem of extending coefficients of the regular representation of H to G. Suppose H normal in G. In 1973 [1] C. Herz proved that for with compact support, for every and for every U neighborhood of in G there is with, and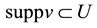. In this work we want to treat the case of non normal subgroups. We succeed assuming that the subgroup H is amenable (Theorem 5). C. Fiorillo obtained [2] already this result assuming however the unimodularity of G and of H. But the AN part of the Iwasawa decomposition of was out of reach. Even for G amenable our result is new: the case of the non-normal copy of 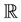in the 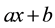-group was also out of reach.

Without control of norm and support of the extension, the theorem has been obtained in 1972 by McMullen [3] . With control of the norm, but not considering the supports, the statement is due Herz [1] (see also [4] ).

2. A Property of Amenable Subgroups

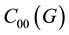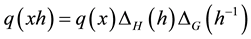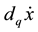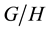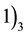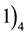We denote by the set of all complex valued continuous functions on G with compact support. We choose a positive continuous function q on G such that, left invariant measures on G and H and a measure on as in Chapter 8 of [5] . The following Lemma will be used in the proof of our main result. See below the steps and of the proof of Lemma 2.

Lemma 1 Let be a locally compact group, a closed amenable subgroup, a compact subset of, a neighborhood of in and. Then there is such that, and

Proof. Let be a compact neighborhood of in with, and By the Proposition 2.1 of [6] (p. 463), there is such that, and such that for every. For every we have

where Consequently

3. Approximation Theorem for Convolution Operators Supported by Subgroups

We refer to [7] for and the canonical map of into (Section p. 101). We denote by the Banach space of all bounded operators of.

We define a family of linear maps of into where is an arbitrary closed

subgroup of. We precise that is the involution of and that for, and we have.

Definition 1. Let be a locally compact group, an arbitrary closed subgroup, and. For we set for

.

Then and where. If then and is contained in [8] .

Lemma 2. Let be a locally compact group, a closed amenable subgroup, , , and an open neighborhood of in. Then there is with, , and such that

for every and every.

Proof. Let with for every. There is a compact

symmetric neighborhood of in with and such that for every. There is open neighborhood of in such that and

are both smaller than for every and for every. We can choose with, for every and such that.

Let be a symmetric compact neighborhood of in contained in with

for every and such that

for every and for every (for and we denote by the function defined on by).

We put, and where is the canonical map of onto.

By the preceding Lemma there is with and such that

is smaller than

and also smaller than

for every. We finally put , and.

1) For every and every we have

.

We show at first that

From

we obtain indeed

.

For every we have

.

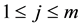
We have

.

But for every

and therefore

consequently

For every we have

As above

taking in account that we obtain

.

Proof of Using and one obtains an estimate for. We finish then the proof of 1) using.

2) For every and every we have

By the Corollary 6 of section 7.2 p.112 of [7]

Consequently

But by definition of for every we have

3) End of the proof of Lemma 2. We are now able to define the functions and of the Lemma and. Using and we get

Clearly and. It remains to show that. We have

But for

hence and similarly, we finally get.

Theorem 3 Let be a locally compact group, a closed amenable subgroup, , a sequence of, a sequence of, and an open neighborhood of in. Suppose that

the series converges. Then there is with, ,

and such that

for every

Proof. We choose with

1) There is with , and such that

for every.

There are and sequences of with

and

for every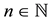. From the convergence of follows the existence of such that

By Lemma 2 there is with, ,

and such that

for every and every. Consequently

2) End of the proof of Theorem 3. It suffices to put and to obtain and

4. The Main Result

Definition 2 Let be a locally compact group, an arbitrary closed subgroup, and For we put

where and are sequences of such that converges and such that

.

Then is a linear map of into, for and one has

, and [8] .

Corollary 4 Let be a locally compact group, a closed amenable subgroup, , , and a neighborhood of in. Then there are with

, and.

Proof. There are sequences of such that converges and such that

. Let be an open neighborhood of in such that. By Theorem 3 there

is with, , and such that

for every.

Consider an arbitrary with. From

and

we get and therefore

The following theorem is the main result of the paper.

Theorem 5 Let be a locally compact group, a closed amenable subgroup, , , and a neighborhood of in. Then there is with and

Proof. This proof is identical with the one of Proposition ii) p. 115 of [1] . Let be an open neighborhood of in such that the closure of in is compact and contained in. Using the Corollary 4 we show by induction the existence of a sequence of and of a sequence of such that, , , ,

and The function satisfies all the requirements.

Cite this paper

AntoineDerighetti, (2014) Amenability and the Extension Property. Applied Mathematics,05,2945-2951. doi: 10.4236/am.2014.519279

References