Applied Mathematics
Vol.5 No.14(2014), Article
ID:48161,7
pages
DOI:10.4236/am.2014.514207
The Construction of Pairwise Additive Minimal BIB Designs with Asymptotic Results
Kazuki Matsubara1, Sanpei Kageyama2
1Graduate School of Science, Hiroshima University, Higashi-Hiroshima, Japan
2Hiroshima Institute of Technology, Hiroshima, Japan
Email: d122307@hiroshima-u.ac.jp, s.kageyama.4b@it-hiroshima.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 21 April 2014; revised 28 May 2014; accepted 12 June 2014
Abstract
An asymptotic existence of balanced incomplete block (BIB) designs and pairwise balanced designs (PBD) has been discussed in [1] -[3] . On the other hand, the existence of additive BIB designs and pairwise additive BIB designs with ![]() and
and ![]() has been discussed with direct and recursive constructions in [4] -[8] . In this paper, an asymptotic existence of pairwise additive BIB designs is proved by use of Wilson’s theorem on PBD, and also for some
has been discussed with direct and recursive constructions in [4] -[8] . In this paper, an asymptotic existence of pairwise additive BIB designs is proved by use of Wilson’s theorem on PBD, and also for some ![]() and
and ![]() the exact existence of
the exact existence of ![]() pairwise additive BIB designs with block size
pairwise additive BIB designs with block size ![]() and
and ![]() is discussed.
is discussed.
Keywords:Incidence Matrix, Pairwise Balanced Design (PBD), Balanced Incomplete Block Design (BIBD), Additive BIB Design, Pairwise Additive BIB Design, Wilson’s Theorem

1. Introduction
A pairwise balanced design (PBD) of order  with block sizes in a set
with block sizes in a set ![]() is a system
is a system![]() , where
, where ![]() is a finite set (the point set) of cardinality
is a finite set (the point set) of cardinality  and
and ![]() is a family of subsets (blocks) of
is a family of subsets (blocks) of ![]() such that 1) if
such that 1) if![]() , then
, then ![]() and 2) every pair of distinct elements of
and 2) every pair of distinct elements of ![]() occurs in
occurs in ![]() blocks of
blocks of ![]() [9] . This is denoted by
[9] . This is denoted by![]() . When
. When![]() , a
, a  is especially called a balanced incomplete block (BIB) design, where
is especially called a balanced incomplete block (BIB) design, where![]() , each block contains
, each block contains 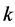 different points and each point appears in
different points and each point appears in 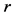 different blocks [10] . This is denoted by
different blocks [10] . This is denoted by ![]() or
or![]() . It is well known that necessary conditions for the existence of a
. It is well known that necessary conditions for the existence of a ![]() are
are
 . (1.1)
. (1.1)
Let 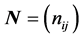 be the
be the  incidence matrix of a BIB design, where
incidence matrix of a BIB design, where ![]() or 0 for all
or 0 for all ![]() and
and![]() , according as the i-th point occurs in the j-th block or otherwise. Hence the incidence matrix
, according as the i-th point occurs in the j-th block or otherwise. Hence the incidence matrix ![]() satisfies the conditions: 1)
satisfies the conditions: 1) 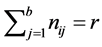 for all
for all![]() , 2)
, 2) 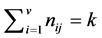 for all
for all![]() , 3)
, 3) 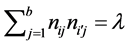 for all
for all![]() .
.
Let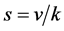 , where
, where 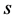 need not be an integer unlike other parameters. Further let
need not be an integer unlike other parameters. Further let![]() . A set of
. A set of ![]()
![]() is called
is called ![]() pairwise additive BIB designs if
pairwise additive BIB designs if ![]() corresponding incidence matrices
corresponding incidence matrices 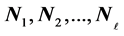 of the BIB design satisfy that
of the BIB design satisfy that ![]() is the incidence matrix of a BIBD(
is the incidence matrix of a BIBD(
![]() ) for any distinct
) for any distinct![]() . When
. When![]() , this is especially called additive BIB designs [6] [7] .
, this is especially called additive BIB designs [6] [7] .
It is clear by the definition that the existence of ![]() pairwise additive
pairwise additive ![]() implies the existence of
implies the existence of ![]() pairwise additive
pairwise additive ![]() for any
for any![]() . Hence, for given parameters
. Hence, for given parameters![]() , the larger
, the larger ![]() is, the more difficult a construction problem of
is, the more difficult a construction problem of ![]() pairwise additive BIB designs is.
pairwise additive BIB designs is.
In pairwise additive![]() , since a sum of any two incidence matrices yields a BIB design, it is seen [7] that
, since a sum of any two incidence matrices yields a BIB design, it is seen [7] that
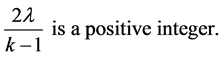 (1.2)
(1.2)
It follows from (1.2) that the existence of ![]() pairwise additive
pairwise additive ![]() implies
implies

Pairwise additive ![]() are said to be minimal if
are said to be minimal if ![]() or
or 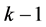 according as
according as 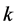 is odd or even.
is odd or even.
Some classes of ![]() pairwise additive
pairwise additive ![]() are constructed in [4] -[8] . It is clear by the definition that
are constructed in [4] -[8] . It is clear by the definition that . The purpose of this paper is to show that, for a given odd prime power
. The purpose of this paper is to show that, for a given odd prime power 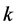 and a given positive integer
and a given positive integer![]() , the necessary conditions (1.1) for the existence of
, the necessary conditions (1.1) for the existence of ![]() pairwise additive minimal
pairwise additive minimal  are asymptotically sufficient on
are asymptotically sufficient on![]() . In particular, for the existence of
. In particular, for the existence of ![]() pairwise additive minimal
pairwise additive minimal![]() , (1.1) is asymptotically sufficient, i.e., there are
, (1.1) is asymptotically sufficient, i.e., there are ![]() pairwise additive minimal
pairwise additive minimal ![]() for sufficiently larger
for sufficiently larger![]() , even if
, even if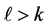 . Furthermore, as the exact existence, it is shown that there are 2 pairwise additive
. Furthermore, as the exact existence, it is shown that there are 2 pairwise additive ![]() for any positive integer
for any positive integer ![]() except possibly for 12 values.
except possibly for 12 values.
2. 
The existence of ![]() is reviewed along with necessary and asymptotically sufficient conditions.
is reviewed along with necessary and asymptotically sufficient conditions.
Let ![]() be a set of positive integers and
be a set of positive integers and
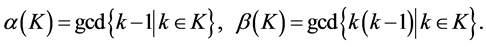
Necessary conditions for the existence of a ![]() are known as follows.
are known as follows.
Lemma 2.1 [2] Necessary conditions for the existence of a ![]() are
are
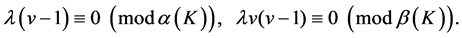 (2.1)
(2.1)
Wilson [3] proved the asymptotic existence as Theorem 2.2 below shows.
Theorem 2.2 The necessary conditions (2.1) for the existence of a ![]() are asymptotically sufficient.
are asymptotically sufficient.
For any set ![]() of positive integers and any positive integer
of positive integers and any positive integer![]() , let
, let ![]() denote the smallest integer such that there are
denote the smallest integer such that there are ![]() for every integer
for every integer 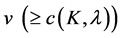 satisfying (2.1). Then Theorem 2.2 states the existence of
satisfying (2.1). Then Theorem 2.2 states the existence of![]() . On the other hand, some explicit bound for
. On the other hand, some explicit bound for ![]() was provided as follows.
was provided as follows.
Lemma 2.3 [11] There are 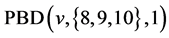 for all positive integers
for all positive integers![]() .
.
Especially, for a set ![]() being a set of prime powers of form
being a set of prime powers of form![]() ,
,  is shown as follows.
is shown as follows.
Lemma 2.4 ([12] Theorem 19.69) Let ![]() be a set of prime powers of form
be a set of prime powers of form ![]() with a positive integer
with a positive integer![]() . Then there are
. Then there are 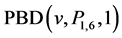 for all positive integers
for all positive integers![]() , except possibly for
, except possibly for ![]()
![]() .
.
3. Construction by 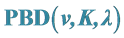
In this section, a method of constructing pairwise additive BIB designs through ![]() is provided.
is provided.
The following simple method is useful to construct pairwise additive BIB designs.
Lemma 3.1 The existence of a ![]() and
and ![]() pairwise additive
pairwise additive ![]() for any
for any 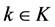 implies the existence of
implies the existence of ![]() pairwise additive
pairwise additive![]() .
.
Proof. Let ![]() be the
be the ![]() and
and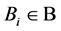 ,
,![]() . On the set
. On the set![]() , let a block set
, let a block set ![]() with all block size
with all block size ![]() be formed by the
be formed by the ![]() pairwise additive
pairwise additive ![]() for each
for each![]() . Then it follows that the
. Then it follows that the
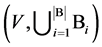 is the required BIB design.
is the required BIB design. 
For example, Lemma 3.1 yields the following.
Theorem 3.2 There are 4 pairwise additive ![]() for any integer
for any integer![]() .
.
Proof. It follows from the fact ([4] [6] ) that there are additive![]() , 4 pairwise additive
, 4 pairwise additive ![]() and additive
and additive![]() . Hence Lemmas 2.3 and 3.1 can yield the required designs.
. Hence Lemmas 2.3 and 3.1 can yield the required designs. 
As the next case of block sizes, 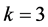 is considered. A concept of
is considered. A concept of ![]() pairwise additive
pairwise additive ![]() has been discussed as a compatibly nested minimal partition in [12] , which shows the existence of pairwise additive
has been discussed as a compatibly nested minimal partition in [12] , which shows the existence of pairwise additive ![]() as follows.
as follows.
Lemma 3.3 ([12] ; Theorem 22.12) Let ![]() be an odd prime power for a positive integer
be an odd prime power for a positive integer![]() . Then there are
. Then there are ![]() pairwise additive
pairwise additive![]() .
.
Lemmas 2.4, 3.1 and 3.3 can produce the following.
Theorem 3.4 ([12] ; Theorem 22.13) There are 2 pairwise additive ![]() for all positive integers
for all positive integers![]() , except possibly for
, except possibly for 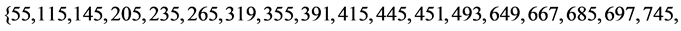
![]()
 .
.
Theorem 3.4 will be improved as in Theorem 6.7.
4. Some Class of Pairwise Additive 
In this section, a necessary condition for the existence of pairwise additive 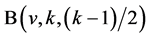 being minimal is provided and then some classes of
being minimal is provided and then some classes of ![]() pairwise additive
pairwise additive 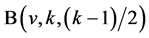 and (
and (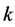 pairwise) additive
pairwise) additive 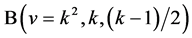 are constructed.
are constructed.
Now (1.1) implies that necessary conditions for the existence of pairwise additive 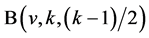 are
are
![]()
Furthermore, the following is given.
Theorem 4.1 When  is an odd prime power, necessary conditions for the existence of pairwise additive
is an odd prime power, necessary conditions for the existence of pairwise additive 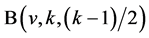 are
are
![]() (4.1)
(4.1)
Proof. Since ![]() and
and![]() , when
, when 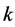 is an odd prime power, it is shown that either
is an odd prime power, it is shown that either ![]() or
or![]() . Hence
. Hence ![]() implies
implies![]() .
. 
When  is an odd prime power, a class of pairwise additive
is an odd prime power, a class of pairwise additive  is obtained as follows. This observation shows a generalization of Lemma 3.3.
is obtained as follows. This observation shows a generalization of Lemma 3.3.
Theorem 4.2 Let both 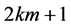 and
and  be odd prime powers for a positive integer
be odd prime powers for a positive integer![]() . Then there are
. Then there are 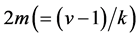 pairwise additive
pairwise additive .
.
Proof. It can be shown that a development of the following initial blocks on ![]() yields incidence matrices
yields incidence matrices  of the required BIB design:
of the required BIB design:

where ![]() is a primitive element of
is a primitive element of ![]() and
and![]() .
. 
Furthermore, the following is known to be provided by recursive constructions with affine resolvable BIB designs. This result will be used in the next section.
Theorem 4.3 [7] Let 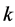 be an odd prime power. Then there are additive
be an odd prime power. Then there are additive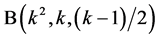 .
.
Especially, when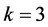 , the further result is known.
, the further result is known.
Theorem 4.4 [8] There are additive B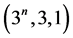 for any positive integer
for any positive integer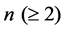 .
.
5. Asymptotic Existence of Pairwise Additive Minimal 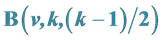
In this section, when 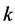 is an odd prime power, an asymptotic existence of pairwise additive
is an odd prime power, an asymptotic existence of pairwise additive 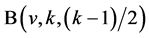 is discussed, and it is shown that the necessary conditions (4.1) for the existence of
is discussed, and it is shown that the necessary conditions (4.1) for the existence of ![]() pairwise additive
pairwise additive 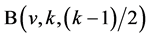 are asymptotically sufficient for a given positive integer
are asymptotically sufficient for a given positive integer![]() .
.
Dirichlet’s theorem on primes is useful for the present discussion.
Theorem 5.1 (Dirichlet) If![]() , then a set of integers of the following form
, then a set of integers of the following form
![]()
contains infinitely many primes.
Now Theorem 5.1 yields the following.
Lemma 5.2 [13] For any positive even integer![]() , there are primes
, there are primes ![]() and
and ![]() for which
for which ![]() and
and .
.
In the proof of Lemma 5.2 (i.e., Lemma 3.4 in [13] ), primes ![]() and
and ![]() are obtained by using Theorem 5.1. Thus Lemma 5.2 implies the existence of sufficiently large primes
are obtained by using Theorem 5.1. Thus Lemma 5.2 implies the existence of sufficiently large primes ![]() and
and ![]() as follows.
as follows.
Lemma 5.3 For a given odd prime power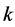 , there are primes
, there are primes ![]() and
and ![]() such that (a)
such that (a)![]() , (b)
, (b)
![]() , (c)
, (c) ![]() and (d)
and (d) ![]() for
for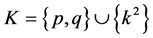 .
.
Proof. Let 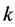 be an odd prime power. Then, for an even integer
be an odd prime power. Then, for an even integer![]() , Lemma 5.2 provides primes
, Lemma 5.2 provides primes ![]() and
and
![]() such that (a)
such that (a)![]() , (b)
, (b) ![]() and
and . Hence it is seen that
. Hence it is seen that![]() ,
, 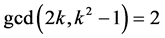 and
and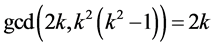 .
.
Now let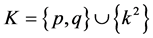 . Then
. Then

which imply (c) and (d). 
Thus one of the main results of this paper is now obtained through conditions (a), (b), (c) and (d) given in Lemma 5.3.
Theorem 5.4 For a given odd prime power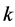 , (4.1) is a necessary and asymptotically sufficient condition for the existence of
, (4.1) is a necessary and asymptotically sufficient condition for the existence of 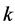 pairwise additive B
pairwise additive B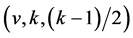 .
.
Proof (sufficiency). Let ![]() and
and ![]() be primes as in Lemma 5.3 with
be primes as in Lemma 5.3 with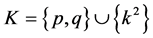 . Then conditions (c) and (d) show that there are
. Then conditions (c) and (d) show that there are ![]() for sufficiently large
for sufficiently large  satisfying (4.1), on account of Theorem 2.2. Conditions (a) and (b) show that there are
satisfying (4.1), on account of Theorem 2.2. Conditions (a) and (b) show that there are ![]() pairwise additive
pairwise additive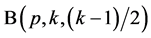 ,
, ![]() pairwise additive
pairwise additive  and additive
and additive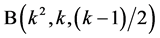 , on account of Theorems 4.2 and 4.3. Hence the required designs can be obtained on account of Lemma 3.1.
, on account of Theorems 4.2 and 4.3. Hence the required designs can be obtained on account of Lemma 3.1. 
Unfortunately, by use of Theorem 5.4 we cannot show the existence of ![]() pairwise additive
pairwise additive  for
for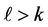 , since an additive
, since an additive 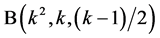 means
means 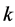 pairwise additive
pairwise additive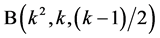 .
.
Next, for a given odd prime power  and a given positive integer
and a given positive integer![]() , even if
, even if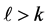 , the existence of
, the existence of ![]()
pairwise additive 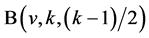 is discussed for sufficiently large
is discussed for sufficiently large![]() .
.
Lemma 5.5 For a given odd prime power 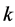 and a given positive integer
and a given positive integer![]() , there are primes
, there are primes ![]() and
and ![]() such that (a)
such that (a) , (b)
, (b) ![]() and (c)
and (c)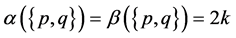 .
.
Proof. Let 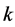 be an odd prime power and
be an odd prime power and ![]() be a positive integer. Then, for a positive integer
be a positive integer. Then, for a positive integer![]() , Lemma 5.2 provides primes p and q such that (a) p > q >
, Lemma 5.2 provides primes p and q such that (a) p > q >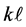 , (b)
, (b) ![]() and
and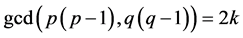 . Hence it is seen that
. Hence it is seen that ![]() and (c) holds.
and (c) holds. 
Thus the following result is obtained through conditions (a), (b) and (c) as in Lemma 5.5.
Theorem 5.6 For a given odd prime power 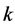 and a given positive integer
and a given positive integer![]() , there are
, there are ![]() pairwise additive
pairwise additive  for sufficiently large
for sufficiently large![]() .
.
Proof. Let ![]() and
and ![]() be primes as in Lemma 5.5. Then it follows from (c) that there are
be primes as in Lemma 5.5. Then it follows from (c) that there are 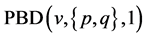
for sufficiently large![]() , on account of Theorem 2.2. Also Theorem 4.2 along with conditions (a) and (b) shows that there are
, on account of Theorem 2.2. Also Theorem 4.2 along with conditions (a) and (b) shows that there are ![]() pairwise additive
pairwise additive 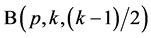 and
and ![]() pairwise additive
pairwise additive . Thus the required designs are obtained on account of Lemma 3.1.
. Thus the required designs are obtained on account of Lemma 3.1. 
6. Pairwise Additive 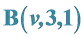
In this section, the existence of pairwise additive ![]() is discussed. At first it is shown that there are
is discussed. At first it is shown that there are ![]() pairwise additive
pairwise additive ![]() for sufficiently large
for sufficiently large![]() , even if
, even if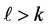 . Furthermore, the exact existence of 2 pairwise additive
. Furthermore, the exact existence of 2 pairwise additive ![]() with
with ![]() is discussed by providing direct and recursive constructions of pairwise additive
is discussed by providing direct and recursive constructions of pairwise additive![]() . Finally, it is shown that there are 2 pairwise additive
. Finally, it is shown that there are 2 pairwise additive ![]() for any
for any ![]() except possibly for 12 values.
except possibly for 12 values.
Three classes of pairwise additive ![]() are given as in Lemma 3.3 and Theorems 3.4 and 4.4. For
are given as in Lemma 3.3 and Theorems 3.4 and 4.4. For![]() , 15 is the smallest value of
, 15 is the smallest value of 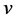 for which the existence of 2 pairwise additive
for which the existence of 2 pairwise additive ![]() is unknown in literature. Hence at first this case is individually considered here.
is unknown in literature. Hence at first this case is individually considered here.
Lemma 6.1 There are 2 pairwise additive![]() .
.
Proof. It can be shown that a development of the following initial blocks on 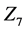 with the index being fixed yields incidence matrices
with the index being fixed yields incidence matrices 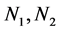 of the required BIB design:
of the required BIB design:

with 15 elements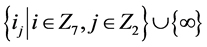 . Here, in general
. Here, in general![]() .
. 
Now, ![]() pairwise additive
pairwise additive ![]() with sufficiently large
with sufficiently large ![]() are obtained as follows. This shows an extension of Theorem 5.4 with
are obtained as follows. This shows an extension of Theorem 5.4 with .
.
Theorem 6.2 For a given positive integer![]() , even if
, even if![]() , there are
, there are ![]() pairwise additive
pairwise additive ![]() with sufficiently large
with sufficiently large![]() .
.
Proof. Let 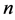 be a positive integer satisfying
be a positive integer satisfying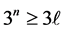 . Then (
. Then (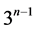 pairwise) additive
pairwise) additive  are constructed by Theorem 4.4, and there are primes
are constructed by Theorem 4.4, and there are primes ![]() and
and ![]() such that
such that![]() ,
, ![]() and
and
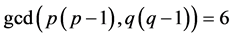 , on account of Lemma 5.2. Furthermore, since
, on account of Lemma 5.2. Furthermore, since ![]() and
and ![]() with
with , there are
, there are 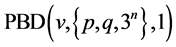 for sufficiently large
for sufficiently large![]() , on account of Theorem 2.2. Hence
, on account of Theorem 2.2. Hence ![]() pairwise additive
pairwise additive ![]() for sufficiently large
for sufficiently large ![]() can be constructed by Lemma 3.1 with
can be constructed by Lemma 3.1 with ![]() pairwise additive
pairwise additive![]() ,
, ![]() pairwise additive
pairwise additive ![]()
and additive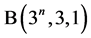 .
. 
Next, some recursive constructions of pairwise additive ![]() are provided. A combinatorial structure is here introduced. A transversal design, denoted by TD
are provided. A combinatorial structure is here introduced. A transversal design, denoted by TD![]() , is a triple
, is a triple ![]() such that 1)
such that 1) ![]() is a set of
is a set of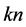 elements, 2)
elements, 2) 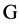 is a partition of
is a partition of ![]() into
into 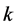 classes (groups), each of size
classes (groups), each of size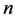 , 3)
, 3) ![]() is a family of k-subsets (blocks) of
is a family of k-subsets (blocks) of![]() , 4) every unordered pair of elements from the same group is not contained in any block, and 5) every unordered pair of elements from other groups is contained in exactly
, 4) every unordered pair of elements from the same group is not contained in any block, and 5) every unordered pair of elements from other groups is contained in exactly ![]() blocks. When
blocks. When![]() , we simply write
, we simply write![]() , where
, where 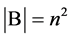 [14] .
[14] .
Since it is known [14] that the existence of a ![]() is equivalent to the existence of
is equivalent to the existence of  mutually orthogonal latin squares of order
mutually orthogonal latin squares of order , the following result can be obtained, when
, the following result can be obtained, when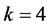 .
.
Lemma 6.3 [14] There exists a ![]() for all
for all ![]() except for
except for ![]() and possibly for
and possibly for![]() .
.
A method of construction is presented, similarly to a recursive construction given in [4] , by use of![]() .
.
Theorem 6.4 The existence of ![]() pairwise additive
pairwise additive![]() ,
, ![]() pairwise additive
pairwise additive ![]() and a
and a ![]() implies the existence of
implies the existence of ![]() pairwise additive
pairwise additive![]() .
.
Proof. Let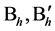 ,
,  , be block sets of
, be block sets of ![]() pairwise additive
pairwise additive ![]() and
and ![]() pairwise additive
pairwise additive
![]() respectively as
respectively as
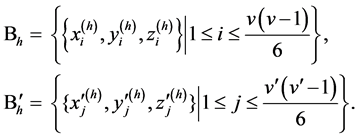
and let![]() ,
,  and
and![]() , denote an element which occurs in both the m-th block of a
, denote an element which occurs in both the m-th block of a![]() and the n-th group. Then it can be shown that the following
and the n-th group. Then it can be shown that the following ![]() incidence matrices yield the required
incidence matrices yield the required ![]() pairwise additive BIB designs with
pairwise additive BIB designs with 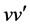 elements denoted by
elements denoted by ![]() for
for ![]() and
and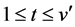 :
:

where ![]() and
and .
. 
Another recursive method is presented.
Theorem 6.5 The existence of ![]() pairwise additive
pairwise additive![]() ,
, ![]() pairwise additive
pairwise additive ![]() and a
and a ![]() implies the existence of
implies the existence of ![]() pairwise additive
pairwise additive![]() .
.
Proof. Let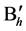 ,
, 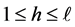 , be a block set similarly to the proof of Theorem 6.4 and let
, be a block set similarly to the proof of Theorem 6.4 and let ,
, 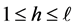 , be a block set of
, be a block set of ![]() pairwise additive
pairwise additive![]() , where
, where

with ![]() elements
elements 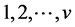 and
and![]() . Also let
. Also let![]() ,
,  and
and![]() , denote an element which occurs in both the m-th block of a
, denote an element which occurs in both the m-th block of a ![]() and the n-th group. Then the following
and the n-th group. Then the following ![]() incidence matrices can yield the required
incidence matrices can yield the required ![]() pairwise additive BIB designs with
pairwise additive BIB designs with 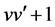 elements denoted by
elements denoted by ![]() for
for ![]() and
and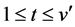 , and
, and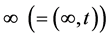 :
:
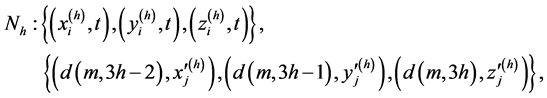
where ![]() and
and .
. 
Now 2 pairwise additive ![]() are more obtained.
are more obtained.
Lemma 6.6 There are 2 pairwise additive ![]() for
for![]() .
.
Proof. For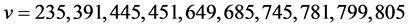 , Theorem 6.5 with
, Theorem 6.5 with
![]()
provides the required BIB designs respectively, because 2 pairwise additive ![]() and 2 pairwise additive
and 2 pairwise additive ![]() are obtained by use of Theorems 3.4 and 4.4 and Lemma 6.1, and a
are obtained by use of Theorems 3.4 and 4.4 and Lemma 6.1, and a ![]() is also obtained by Lemma 6.3.
is also obtained by Lemma 6.3. 
Hence on account of Lemma 6.6, the following result can be obtained. This improves Theorem 3.4.
Theorem 6.7 There are 2 pairwise additive ![]() for any positive integer
for any positive integer![]() , except possibly for
, except possibly for![]() .
.
Unfortunately, we cannot clear such 12 values displayed in Theorem 6.7. Furthermore, the existence of 2 pairwise additive ![]() has not been known except for
has not been known except for ![]() being
being ![]() and 15 in Theorem 4.4 and Lemma 6.1.
and 15 in Theorem 4.4 and Lemma 6.1.
Remark. Since Theorem 4.2 can be valid for a given odd integer , Theorem 5.6 is extended for a given odd integer
, Theorem 5.6 is extended for a given odd integer . On the other hand, when
. On the other hand, when 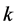 is an even prime power, an asymptotic existence of pairwise additive minimal
is an even prime power, an asymptotic existence of pairwise additive minimal  is proved by some methods similar to Theorems 4.2, 4.3, 5.4 and 5.6. In particular, for
is proved by some methods similar to Theorems 4.2, 4.3, 5.4 and 5.6. In particular, for![]() , the complete existence of
, the complete existence of ![]() pairwise additive
pairwise additive ![]() has been shown in [4] [5] . However, in general, the exact existence of
has been shown in [4] [5] . However, in general, the exact existence of ![]() pairwise additive minimal
pairwise additive minimal ![]() with (1.1) could not be shown in this paper.
with (1.1) could not be shown in this paper.
References
- Wilson, R.M. (1972) An Existence Theory for Pairwise Balanced Designs I. Journal of Combinatorial Theory, Series A, 13, 220-245. http://dx.doi.org/10.1016/0097-3165(72)90028-3
- Wilson, R.M. (1972) An Existence Theory for Pairwise Balanced Designs II. Journal of Combinatorial Theory, Series A, 13, 246-273. http://dx.doi.org/10.1016/0097-3165(72)90029-5
- Wilson, R.M. (1975) An Existence Theory for Pairwise Balanced Designs III. Journal of Combinatorial Theory, Series A, 18, 71-79. http://dx.doi.org/10.1016/0097-3165(75)90067-9
- Matsubara, K. and Kageyama, S. (2013) The Existence of Two Pairwise Additive for any . Journal of Statistical Theory and Practice, 7, 783-790. http://dx.doi.org/10.1080/15598608.2013.783742
- Matsubara, K. and Kageyama, S. (to be Published) The Existence of 3 Pairwise Additive for Any . Journal of Combinatorial Mathematics and Combinatorial Computing.
- Matsubara, K., Sawa, M., Matsumoto, D., Kiyama, H. and Kageyama, S. (2006) An Addition Structure on Incidence Matrices of a BIB Design. Ars Combinatoria, 78, 113-122.
- Sawa, M., Matsubara, K., Matsumoto, D., Kiyama, H. and Kageyama, S. (2007) The Spectrum of Additive BIB Designs. Journal of Combinatorial Designs, 15, 235-254. http://dx.doi.org/10.1002/jcd.20147
- Sawa, M., Kageyama, S. and Jimbo, M. (2008) Compatibility of BIB Designs. Statistics and Applications, 6, 73-89.
- Mullin, R.C. and Gronau, H.D.O.F. (2007) PBDs and GDDs: The Basics. In: Colbourn, C.J. and Dinitz, J.H., Eds., The CRC Handbook of Combinatorial Designs, 2nd Edition, CRC Press, Boca Raton, 160-193.
- Raghavarao, D. (1988) Constructions and Combinatorial Problems in Design of Experiments. Dover, New York.
- Colbourn, C.J. and Ling, A.C.H. (1997) Pairwise Balanced Designs with Block Sizes 8, 9 and 10. Journal of Combinatorial Theory, Series A, 77, 228-245. http://dx.doi.org/10.1006/jcta.1997.2742
- Colbourn, C.J. and Rosa, A. (1999) Triple Systems. Oxford Press, New York, 404-406.
- Granville, A. (1988) Nested Steiner n-Cycle Systems and Perpendicular Arrays. Journal of Combinatorial Mathematics and Combinatorial Computing, 3, 163-167.
- Abel, R.J.R., Colbourn, C.J. and Dinitz, J.H. (2007) Mutually Orthogonal Latin Square. In: Colbourn, C.J. and Dinitz, J.H., Eds., The CRC Handbook of Combinatorial Designs, 2nd Edition, CRC Press, Boca Raton, 160-193.

