Applied Mathematics
Vol.5 No.3(2014), Article ID:42643,5 pages DOI:10.4236/am.2014.53035
G-Function Solutions for Schrödinger Equation in Cylindrical Coordinates System
1Nuclear Science Research School, NSTRI, Tehran, Iran
2School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Selangor, Malaysia
Email: apishkoo@gmail.com, maslina@ukm.my
Received October 29, 2013; revised November 29, 2013; accepted December 6, 2013
ABSTRACT
In this paper, the Schrödinger equation is solved by Modified separation of variables (MSV) method suggested by Pishkoo and Darus. Using this method, Meijer’s G-function solutions are derived in cylindrical coordinate system for quantum particle in cylindrical can. All elementary functions and most of the special functions which are the solution of extensive problems in physics and engineering are special cases of Meijer’s G-functions.
Keywords:Meijer’s G-Function; Partial Differential Equation; Modified Separation of Variables; Schrödinger Equation
1. Introduction
Perhaps, Cornelis Simon Meijer (1936) was the first to introduce the G-function in mathematics. This very general function intended to include most of the known special functions as particular cases; and for a long time, many studies have been done involving this type of functions. These functions have a lot of practical applications in the fields of mathematical physics, theoretical physics, mathematical analysis, etc.
Meijer’s G-functions are defined as Mellin-Barnes contour integrals which have been in existence for over 60 years [1-5]. Meijer’s G-function satisfies the linear ordinary differential equation (LODE) of the generalised hypergeometric type whose order is equal to  [6-8]. This fact triggered us to verify the equality conditions between Meijer’s G-function’s LODE and some partial differential equations governing physical phenomena. In physics, we have many ordinary and partial differential equations, in which their solutions are elementary functions, special functions or a combination of both of them. Thus, Meijer’s G-functions can be the solution for many physical problems if the equality requirement between Meijer’s G-function’s LODE and those differential equations are verified. As such, we seek to deduce the solution of physical problems explicitly in terms of Meijer’s G-functions.
[6-8]. This fact triggered us to verify the equality conditions between Meijer’s G-function’s LODE and some partial differential equations governing physical phenomena. In physics, we have many ordinary and partial differential equations, in which their solutions are elementary functions, special functions or a combination of both of them. Thus, Meijer’s G-functions can be the solution for many physical problems if the equality requirement between Meijer’s G-function’s LODE and those differential equations are verified. As such, we seek to deduce the solution of physical problems explicitly in terms of Meijer’s G-functions.
Our previous works had focused on the introduction of the Modified separation of variables method (MSV), and applying it to solve partial differential equation related to the Reaction-Diffusion process [9], Laplace’s diffusion and Schrödinger equations [10-12] which led to representing its solution in terms of Meijer’s Gfunctions. The Cartesian coordinate system is used to derive their solutions. However, in this paper, we obtain G-function solutions for the same problem related to Schrödinger equation, solved by “separation of variables (SV)” in [13], by using modified separation of variables (MSV) method and cylindrical coordinates system as follows.
2. Meijer’s G-Function
We begin with the definition of Meijer’s G-function as the following:
Definition 1 A definition of the Meijer’s G-function is given by the following path integral in the complex plane, called Mellin-Barnes type integral:
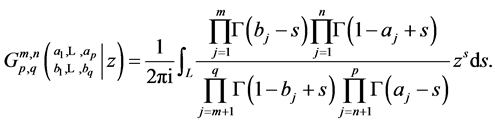 (1.1)
(1.1)
Here, the integers 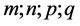 are called “orders” of the G-function, or the components of the order
are called “orders” of the G-function, or the components of the order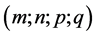 ;
; 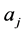 and
and  are called “parameters” and in general, they are complex numbers. The definition holds under the following assumptions:
are called “parameters” and in general, they are complex numbers. The definition holds under the following assumptions: 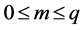 and
and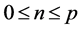 , where
, where  and
and 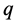 are integer numbers. Subtracting parameters
are integer numbers. Subtracting parameters 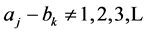 for
for  and
and  imply that no pole of any
imply that no pole of any 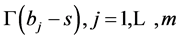 coincides with any pole of any
coincides with any pole of any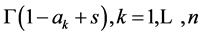 .
.
Exercise 1 Using (1.1), wo obtain the follows ![]() see [14]
see [14]
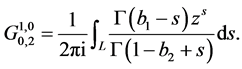 (1.2)
(1.2)
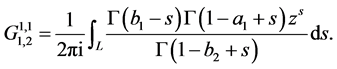 (1.3)
(1.3)
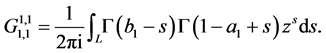 (1.4)
(1.4)
The Meijer’s G-function 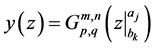 satisfies the linear ordinary differential equation of the generalised hypergeometric type
satisfies the linear ordinary differential equation of the generalised hypergeometric type
 (1.5)
(1.5)
whose order is equal to .
.
Choosing appropriate values for 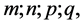 orders of G-functions, Equation (1.5) can be changed to complex first and second order linear differential equations. The following section discusses the properties of the solutions of complex first and second order differential equations, and then studies the properties of coefficient functions of these differential equations in the complex plane.
orders of G-functions, Equation (1.5) can be changed to complex first and second order linear differential equations. The following section discusses the properties of the solutions of complex first and second order differential equations, and then studies the properties of coefficient functions of these differential equations in the complex plane.
We start with using Modified separation of variables method (MSV) in cylindrical coordinates system as follows:
3. The G-Function Solutions for the Schrödinger Equation
When the geometry of the boundaries is cylindrical, the appropriate coordinate system is the cylindrical one. Separation of variables leads to ODEs in which certain constants (eigenvalues) appear. Different choices of signs for these constants can lead to different functional forms of the general solution. Thus general form of the solution is indeterminate. However, once the boundary conditions are imposed, the unique solutions will emerge regardless of the initial functional form of the solutions. Writing  as a product of three functions,
as a product of three functions, 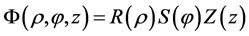 and a separation of variables transforms Laplace’s equation,
and a separation of variables transforms Laplace’s equation, ![]() , into three ODEs:
, into three ODEs:
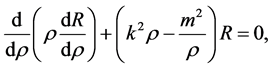
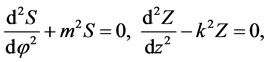
where in anticipation of the correct BCs, we have written the constants as 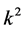 and
and 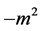 with
with 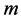 an integer.
an integer.
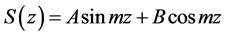
is a combination of two independent solutions deduced by “separation of variables method” or
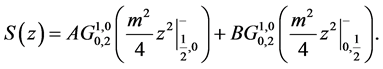
is a combination of two independent solutions deduced by “modified separation of variables method”. Similarly
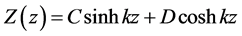
is a combination of two independent solutions deduced by “separation of variables method” or
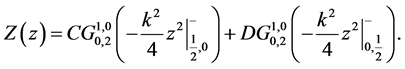
is a combination of two independent solutions deduced by “modified separation of variables method”.
1) For , (1.5) reduces to
, (1.5) reduces to

By changing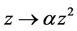 , we have
, we have

By multiplying both sides of the equation by −4, we have
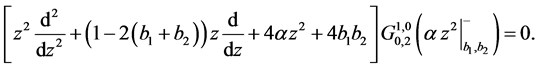
On the other hand, let Bessel equation
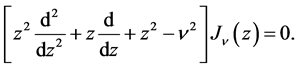
The conditions for equivalence or these two differential equations are
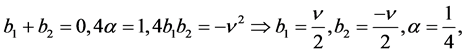
and its solutions is

4. Quantum Particle in a Cylindrical Can
Exercise 2 Considering a quantum particle in a cylindrical can, for an atomic particle of mass μ confined in a cylindrical can of length L and radius a, the relevant Schrödinger equation is
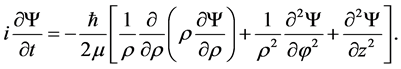
Let us solve this equation subject to the BCs that 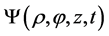 vanishes at the sides of the can by using MSV method.
vanishes at the sides of the can by using MSV method.
Here is the steps: A separation of variables,
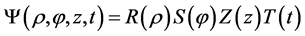 leads to the following ODEs:
leads to the following ODEs:
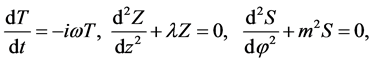 (1.6)
(1.6)
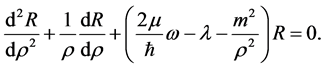 (1.7)
(1.7)
The second DE, the  equation, along with its BCs, constitutes an S-L system with G-function solutions.
equation, along with its BCs, constitutes an S-L system with G-function solutions.
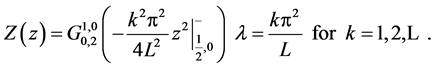
Since the extra condition of periodicity is usually imposed on the potential for variable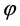 , the third DE, in terms of Meijer’s G-functions, has the general solution.
, the third DE, in terms of Meijer’s G-functions, has the general solution.
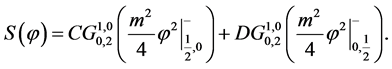
If we let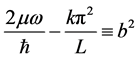 , then the solution of the last equation that is well-behaved is at
, then the solution of the last equation that is well-behaved is at 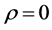 and is
and is  From the last BC, R(a) = 0, we obtain the quantisation condition
From the last BC, R(a) = 0, we obtain the quantisation condition 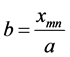 for
for 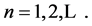
Then, the energy eigenvalues are

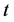 component: for
component: for , (1.5) is reduced to:
, (1.5) is reduced to:
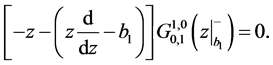
On the other hand,  with changing variable
with changing variable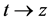 .
.
The condition for the equivalence of these two differential equations is given by the solution of t-component. Thus, the general solution can be written as
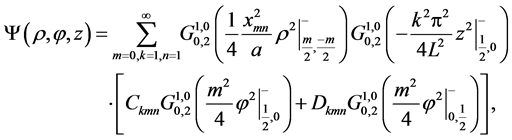 (1.8)
(1.8)
& 
REFERENCES
- V. Kiryakova, “Generalized Fractional Calculus and Applications, Vol. 301,” Chapman & Hall/CRC London, 1994.
- L. Andrews, “Special Functions for Engineers and Applied Mathematicians,” Macmillan, 1985.
- Y. Luck, “The Special Functions and Their Approximations, Complex Variables,” Academic Press, New York, 1969.
- R. Askey, “Meijer G-Function,” Cambridge University Press, Cambridge, 2010.
- A. Klimyik, “Meijer G-Function,” Springer, Berlin, 2001.
- A. Erdelyi, W. Magnus, F. Oberhettinger and F. Tricomi, “Higher Transcendental Functions,” McGraw-Hill, New York, 1953.
- A. Prudnikov, I. Brychkov and O. Marichev, “Integrals and Series: Some More Special Functions,” Gordon & Breach, Philadelphia, 1992.
- A. Kilbas, H. Srivastava and J. Trujillo, “Theory and Applications of Fractional Differential Equations,” Elsevier Amsterdam, 2006.
- A. Pishkoo and M. Darus, “Meijer’s G-Functions (MGFs) in Microand Nanostructures,” Journal of Computational and Theoretical Nanoscience, Vol. 10, No. 10, 2013, pp. 2478-2483. http://dx.doi.org/10.1166/jctn.2013.3234
- A. Pishkoo and M. Darus, “Some Applications of Meijer G-Functions as Solutions of Differential Equations in Physical Models,” Journal of Mathematical Physics, Analysis, Geometry, Vol. 3, No. 9, 2013, pp. 379-391.
- A. Pishkoo and M. Darus, “Meijer’s G-Functions as the Solution of Schrodinger Equation” Proceeding of the 43rd Iranian Mathematics Conference University of Tabriz, Tabriz, 27-30 August 2012.
- A. Pishkoo and M. Darus, “G-Function Solutions for Diffusion and Laplace’s Equations,” Journal of Advances in Mathematics, Vol. 4, No. 1, 2013, pp. 359-365.
- S. Hassani, “Mathematical Physics: A Modern Introduction to Its Foundations,” Springer, New York, 1998.
- A. Pishkoo and M. Darus, “Fractional Differintegral Transformations of Univalent Meijer’s G-Functions,” Journal of Inequalities and Applications, Vol. 2012, 2012, p. 36. http://dx.doi.org/10.1186/1029-242X-2012-36

