Applied Mathematics
Vol.4 No.10B(2013), Article ID:37456,7 pages DOI:10.4236/am.2013.410A2003
FEM Approach for Transient Heat Transfer in Human Eye
Department of Natural Sciences (Mathematics), School of Science, Kathmandu University, Kavre, Nepal
Email: *gokulkc2@gmail.com
Copyright © 2013 Gokul K. C. et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 7, 2013; revised September 7, 2013; accepted September 14, 2013
Keywords: Human Eye; Bio-Heat Transfer; FEM; Numerical Simulations
ABSTRACT
In this paper, a bio-heat transfer model of temperature distribution in human eye is discussed using appropriate boundary conditions for cornea and sclera. Variational finite element method with Crank-Nicolson scheme is used to calculate the transient temperature distribution in normal human eye. The temperature with and without the effect of blood perfusion and metabolism on retina is simulated and compared for various ambient temperatures, evaporation rates and lens thermal conductivities. The obtained results are compared with experimental results and past results found in literatures. The results show that the steady state corneal temperature is achieved in around 31 and 45 minute of exposure at ambient temperatures 10˚C and 50˚C respectively. Steady state eye temperature is achieved earlier at higher evaporation rate. Similar result is achieved for higher lens thermal conductivity and also for lower ambient temperature.
1. Introduction
In a human body the internal body temperature almost remains constant despite the fluctuation of environmental temperatures up to certain limits. The main organ that keeps core temperature constant is dermal part [1]. There is no skin layer to keep the core temperature constant in case of human eye. The skin layer (eyelid) covers eye surface (cornea) for 3 seconds in a minute (in an average). But for 57 seconds in a minute,ocular surface (cornea) has to manage thermal stress of an environment. The human eye is relatively a small and complex organ, consists of several sub domains with different material properties and having complex geometry.
The calculation of the temperature distribution in human eye when it is heated or cooled is an important aspect of the development of infrared and radiofrequency safety guidelines and for hyperthermia and thermo-therapy treatments of various ocular diseases [2]. The severity of the physiological effect produced by small temperature increases can cause eyesight to worsen. Actually, a small temperature increase in the eye of 3˚C - 5˚C leads to induce cataracts formation [3]. Some researchers believe that thermal effect can induce cataracts; other believes that it is the result of other biological and genetic issues. One of the early theory suggested that heat exchanges within the anterior eye caused the cataract. Verhoeff and Bell argued that cataract formed on the posterior surface of the lens because the anterior surface was cooled by circulation of the aqueous humor and so the cornea was air cooled [4]. Investigation in Germany showed that the cataracts were due to the raised temperature induced indirectly through heat absorbed by the iris, where a rich blood supply would be consistent with a high degree of heating. At the same time Salil noticed the rise in cataracts one year after a very hot, dry summer in Iowa, highlighting likely environmental causes of cataracts [4].
Due to convective heat transport of the blood vessels; the blood picks up energy from hot areas and deposits this at cooler area or vice versa. The difficulty of modeling in the eye is due to the impact of blood flow on the heat transfer; however, incorporating the impact of blood flow in heat transport calculation is very important [2]. The temperature inside the human body depends on the degree of temperature, duration of exposure and the environmental conditions which cause heat gain/loss from tissues [1]. Hence, blood flow and time are the main factors that affect temperature distribution in human eye.
Lagendijk [5] used a finite difference method to calculate the temperature distribution in human and rabbit eyes during hyperthermia treatment. The heat transport from the sclera to the surrounding anatomy is described by a single heat transfer coefficient which includes the impact of blood flow in choroid and sclera. Scott [6] utilized finite element method to obtain the temperature profile based on heat conduction using various heat transfer coefficients given by Lagendijk. Amara [7] presented a numerical thermal model of laser-ocular media interaction. Ng and Ooi [8] studied the effect of aqueous humor hydrodynamics on heat transfer within human eye by neglecting blood perfusion and metabolism. They neglected the effects because they assumed that perfusion in iris/cilliary is sufficient to maintain their temperature at 37˚C. Li et al. [9] studied the bio-heat transfer in the human eye, neglecting the effect of perfusion and metabolism, using 3D alpha finite element method. They assumed the contribution due to perfusion and metabolism is very small because they occur only on small part in the human eye. Cvetkovic et al. [10] developed a thermal model and studied effects of pulsed laser in human eye. Narasimhan et al. [11] developed transient model to study heat transfer in human eye undergoing laser surgery. Flyckt et al. [2] studied the impact of choroidal blood flow and scleral convection heat transfer coefficient in human eye.
All the previously developed models have neglected the effects of blood perfusion and metabolism on retina/iris/cilliary body. The significance of blood perfusion and metabolism on the temperature distribution in the eye is debatable, since they take place only on retina, choroid, iris and cilliary body, which constitute very small part of human eye. The blood flow in the iris/sclera part plays significant role to adjust eye temperature with the rest of the body [3]. In [8] it is clearly mentioned that “Due to lack of literature data, the perfusion term is neglected. The effect of this assumption on the accuracy of the model however remaining unknown”. The retina has perhaps the highest oxygen consumption rate (metabolism) of any tissue in the body [12]. Hence it is necessary to investigate the effects of blood perfusion and metabolism in order to obtain a more accurate result. The objective of this paper is to determine the transient temperature distribution in human eye. Hence, this model provides the results for transient temperature distribution including the effect of blood perfusion and metabolism.
2. Model Formulation
The eye is assumed a perfectly bonded solid structure with each component homogeneous. The eye is considered having six major components: cornea, aqueous humor, lens, vitreous humor, retina, and sclera. As sketched on Figure 1, the thickness of cornea, aqueous humor, lens, vitreous humor, retina and sclera have been considered as 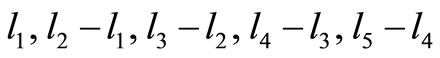 and
and 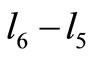 respectively. Similarly,
respectively. Similarly, 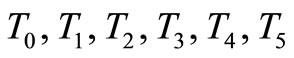 and
and 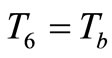 (body core temperature) are the nodal temperatures at a distances
(body core temperature) are the nodal temperatures at a distances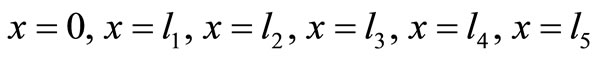 and
and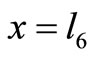 .
.
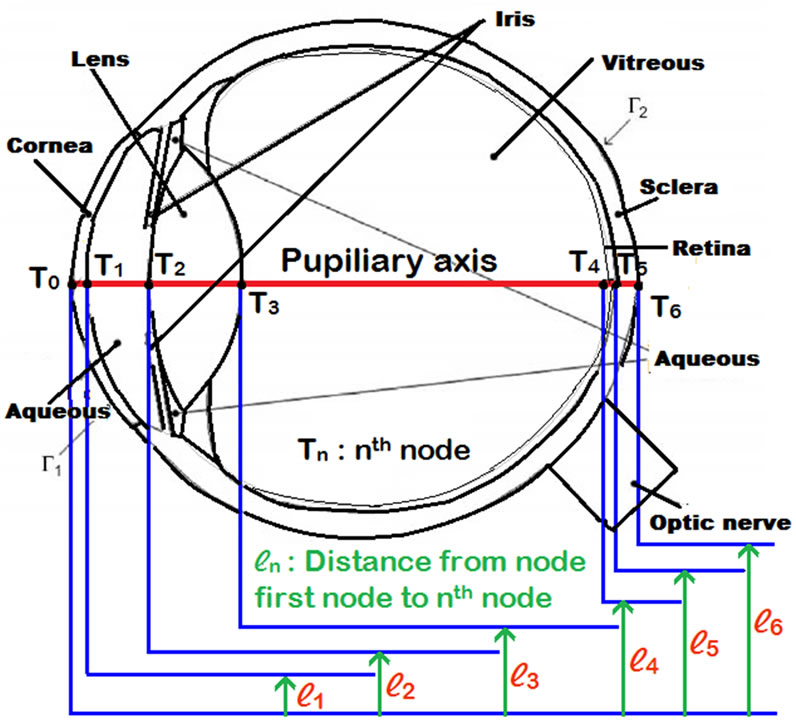
Figure 1. Finite element sketch of human eye.
A one dimensional finite element human eye model has been developed to simulate its thermal unsteady state conditions. The governing differential equation used for heat flow in the human eye due to Pennes [13] is given by:
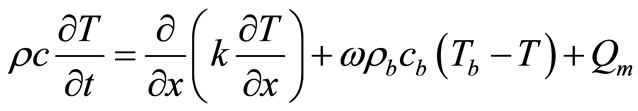 (1)
(1)
where, ρ = tissue density (kg/m3), c = tissue specific heat (J/kg˚C), ρb = blood density (kg/m3), cb = blood specific heat (J/kg˚C), k = tissue thermal conductivity (W/m˚C), ω = volumetric blood perfusion rate per unit volume (s−1), Tb = blood temperature (˚C), T = tissue temperature (˚C), t = time (s), Qm = heat generation due to metabolism (W/m3).
The three terms on the right-hand side of bio-heat Equation (1) are blood conduction, blood perfusion, and metabolism. In this model, the effect of blood perfusion and metabolism is analyzed only on retina.
Boundary conditions for the system can be defined as follows [9,14]:
1) In the back of the eye, heat is transferred from blood via ophthalmic vessels to the sclera:
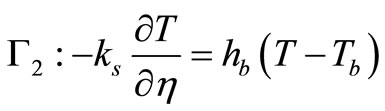 (2)
(2)
where 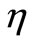 is the normal direction to the surface boundary, ks is the thermal conductivity of sclera, hb is the heat transfer coefficient between blood and eye (W/m2 ˚C), and Tb is blood temperature (˚C).
is the normal direction to the surface boundary, ks is the thermal conductivity of sclera, hb is the heat transfer coefficient between blood and eye (W/m2 ˚C), and Tb is blood temperature (˚C).
2) At the cornea, heat loss from the eye occurs through convection, radiation, and tear evaporation:
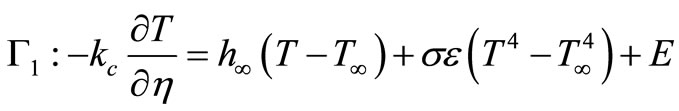 (3)
(3)
where h¥ represents the convection heat transfer coefficient between the cornea and ambient environment (W/m2 ˚C), T¥ is the ambient room temperature (˚C), σ is the Stefan Boltzmann constant (5.67 × 10−8 W/m2˚C4), ε is the emissivity of the cornea, and E is evaporative heat loss (W/m2).
The nonlinear radiation term in the boundary condition (3) is treated by using simple iterative procedure as follows:
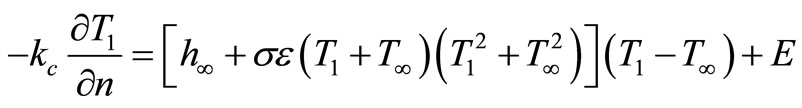 (4)
(4)
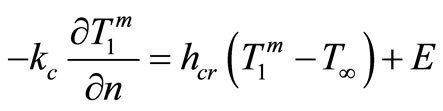 (5)
(5)
where,
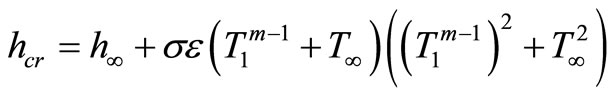 (6)
(6)
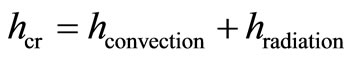
where 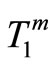 are temperature sequences for
are temperature sequences for 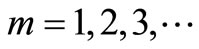 and
and 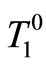 represents an initial guess of temperature.
represents an initial guess of temperature.
The iteration is completed when the convergent condition is satisfied:
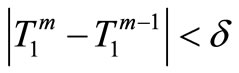 (7)
(7)
where 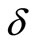 is iteration tolerance.
is iteration tolerance.
The inner body core temperature Tb is assumed to be 37˚C. Therefore, the initial boundary condition is
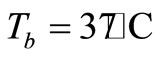 (8)
(8)
The partial differential Equation (1) together with boundary conditions (2) and (5) in one dimensional variational form is:
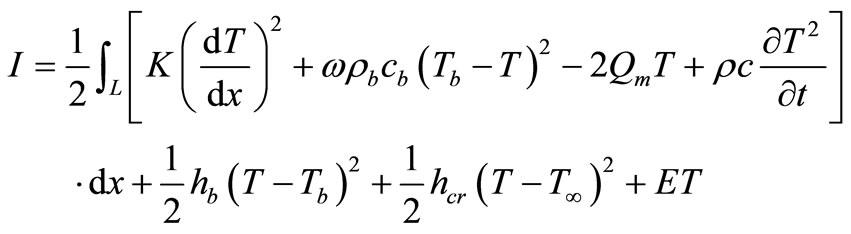 (9)
(9)
We write I separately for the six layers in the following equation:
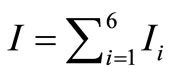 (10)
(10)
Further, to optimize I, we differentiate I partially with respect to Ti and equating to zero, we get,
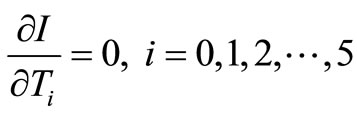 (11)
(11)
The system of Equations (11) can be written in matrix form
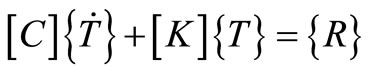 (12)
(12)
where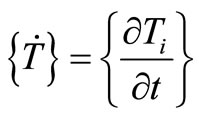 ,
, 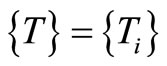 and
and 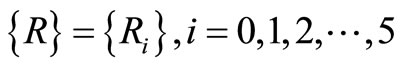 are
are 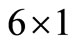 vectors and [C] and [K] are
vectors and [C] and [K] are 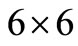 matrices called capacity and conductivity matrices respectively.
matrices called capacity and conductivity matrices respectively.
Now we apply Crank-Nicolson method to solve the system (12) with respect to time, we get the following relation
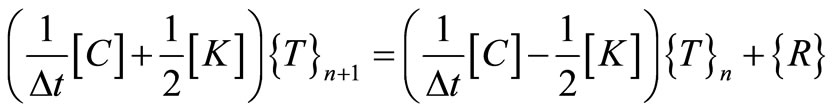 (13)
(13)
where 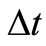 is time interval.
is time interval.
The temperature increases from outer surface of cornea towards eye core when ambient temperature is less than 37˚C and vice versa. Hence, we consider the temperature increases/decreases in linear order towards body core with regard to thickness. For initial nodal temperatures 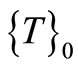 at time
at time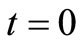 , we assume the following initial condition
, we assume the following initial condition
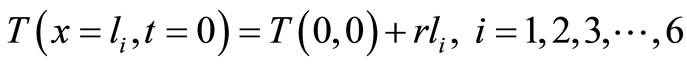 (14)
(14)
where 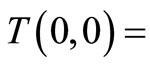 20˚C and
20˚C and 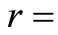 constant to be determined. The Equation (13) is repeatedly solved to get the required nodal temperatures.
constant to be determined. The Equation (13) is repeatedly solved to get the required nodal temperatures.
3. Results and Discussion
To solve equation (13), the following values of parameters are considered [14]: 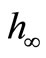 = 10 W/m2 ˚C, hb = 65 W/m2 ˚C, rb = 1060 Kg/m3, cb = 3594 J/Kg ˚C, K1 = 0.580 W/m ˚C, K2 = 0.578 W/m ˚C, K3 = 0.4 W/m ˚C, K4 = 0.603 W/m ˚C, K5 = 0.565 W/m ˚C, K6 = 1.0042 W/m ˚C, l1 = 0.0005 m, l2 = 0.00354 m, l3 = 0.00754 m, l4 = 0.02355 m, l5 = 0.02405 m, l6 = 0.02510 m, w = 0.012 s−1, Qm = 1000 W/m3,
= 10 W/m2 ˚C, hb = 65 W/m2 ˚C, rb = 1060 Kg/m3, cb = 3594 J/Kg ˚C, K1 = 0.580 W/m ˚C, K2 = 0.578 W/m ˚C, K3 = 0.4 W/m ˚C, K4 = 0.603 W/m ˚C, K5 = 0.565 W/m ˚C, K6 = 1.0042 W/m ˚C, l1 = 0.0005 m, l2 = 0.00354 m, l3 = 0.00754 m, l4 = 0.02355 m, l5 = 0.02405 m, l6 = 0.02510 m, w = 0.012 s−1, Qm = 1000 W/m3, 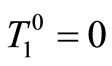 , and
, and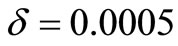 .
.
The numerical calculation for unsteady state temperature distribution is carried out for different parts of human eye with and without taking blood perfusion and metabolism on the retina. The effects of different ambient temperatures, tear evaporation rates and lens thermal conductivities are studied and compared. The results obtained are compared with experimental and other results found in literatures. The overall thermal behavior of human eye is observed for 3600 seconds using one second time step size.
3.1. Effect of Blood Perfusion and Metabolism
The transient temperature distribution of several parts of human eye for 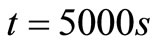 is presented in Figures 2 and 3 below. The parameter values
is presented in Figures 2 and 3 below. The parameter values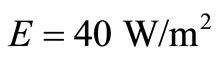 , K3 = 0.4 W/m ˚C and
, K3 = 0.4 W/m ˚C and 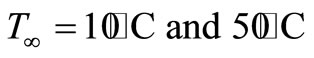 respectively are used for analysis.
respectively are used for analysis.
It can be seen from Figures 2 and 3 that the anterior and posterior part of cornea, aqueous and lens temperatures begin to stabilize around 1870 seconds (approximately 31.17 minutes) and 2740 seconds(approximately 45.67 minutes) respectively. In human eye, heat gain occurs through conduction, perfusion, metabolism, blinking, tear flow, evaporation, and convection but heat loss occurs only through conduction, evaporation, convection and radiation. More factors are involved in heating eye components than cooling. Hence, eye is more vulnerable when it is exposed to high temperatures (high ambient temperatures, hyperthermia treatment, laser surgery etc.) than low (low ambient temperatures, cryosurgery treatment etc). The temperature difference obtained between anterior and posterior parts of cornea are 2.2˚C and 0.65˚C respectively at 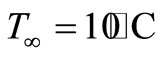 and T∞ = 50˚C. As well the temperature differences between anterior and posterior parts of lens are 0.2˚C and 0.05˚C.
and T∞ = 50˚C. As well the temperature differences between anterior and posterior parts of lens are 0.2˚C and 0.05˚C.
The corneal temperature distribution with and without blood perfusion and metabolism in retina at T∞ = 10˚C and T∞ = 50˚C are shown in Figures 4 and 5 below.
It can be observed from Figures 4 and 5 that when corneal surface temperature is attained steady state in both cases, the temperature differences with and without blood perfusion and metabolism obtained are 0.23˚C and
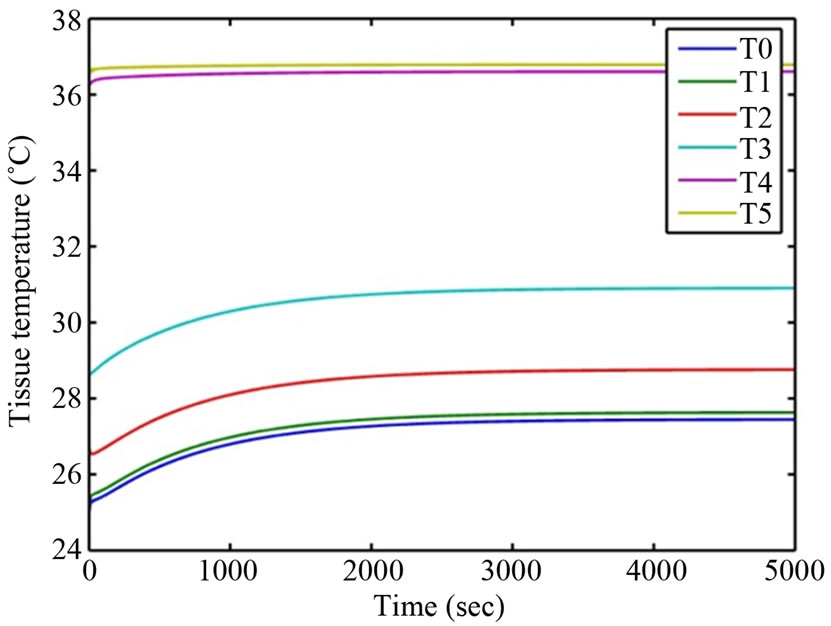
Figure 2. Temperature variation at T∞ = 10˚C.
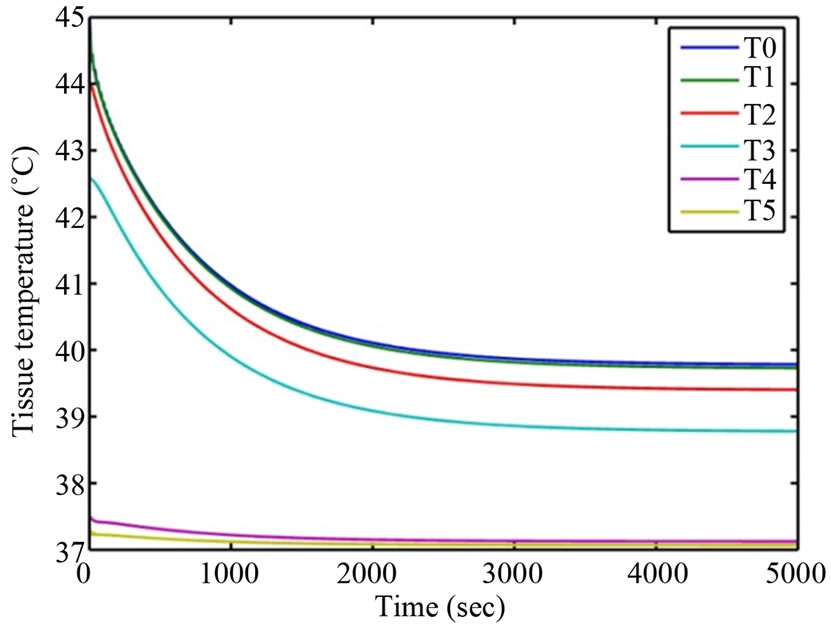
Figure 3. Temperature variation at T∞ = 50˚C.
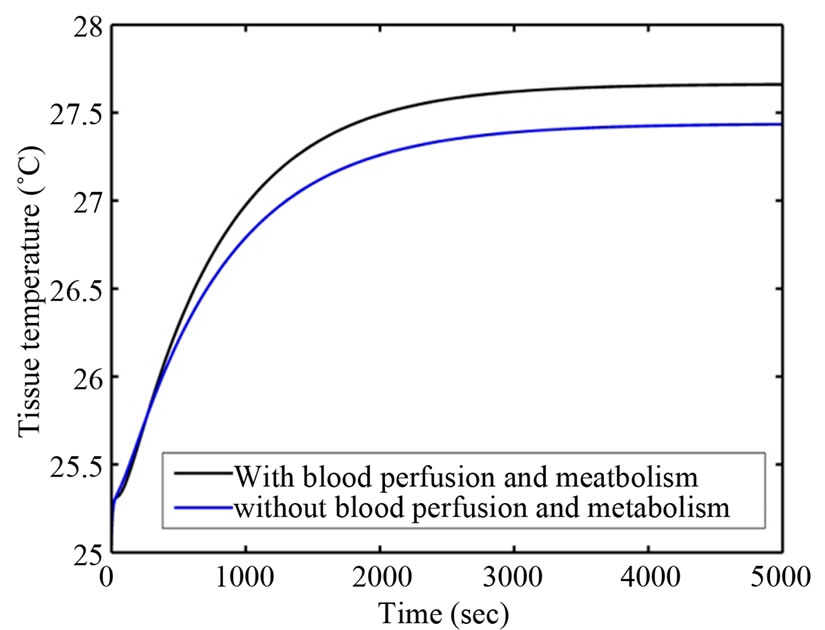
Figure 4. Temperature variation at T∞ = 10˚C.
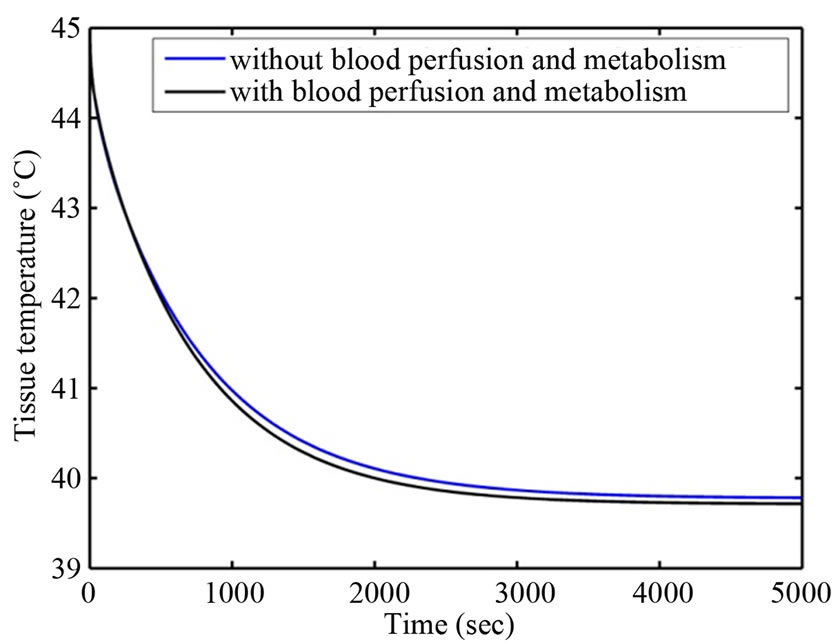
Figure 5. Temperature variation at T∞ = 50˚C.
0.06˚C respectively. Steady state corneal surface temperature is reached earlier in case of having blood perfusion and metabolism in retina. Accordingly, steady state corneal surface temperature is reached earlier at T∞ = 10˚C compared to that at T∞ = 50˚C. This is due to better heating mechanism than cooling in eye.
For further investigation, we now put the effect with blood perfusion and metabolism as Case I and without them as Case II.
3.2. Effect of Tear Evaporation
The corneal surface contains a three-layered structure—a mucoid layer, a thick aqueous layer and thin oily layer. The function of oily layer is to prevent evaporation of tear from the corneal surface. When the oily layer is destroyed, the evaporation rate increases dramatically [15]. Four sets of data values for E equals 20 W/m2, 40 W/m2, 100 W/m2, 180 W/m2 are used in this investigation. The temperature variations for different evaporation rates at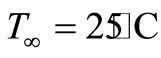 ,
, 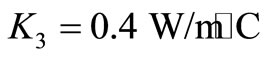 are shown in Figures 6 and 7.
are shown in Figures 6 and 7.
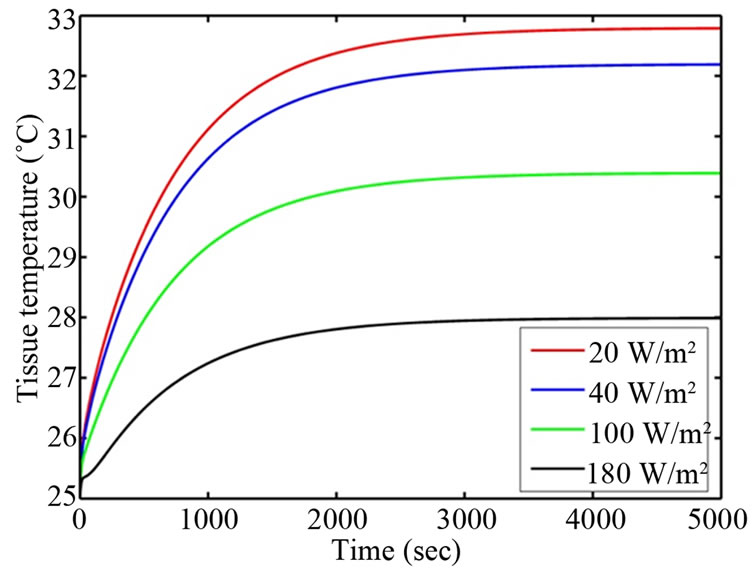
Figure 6. Corneal surface temperature for different evaporation rates (Case I).
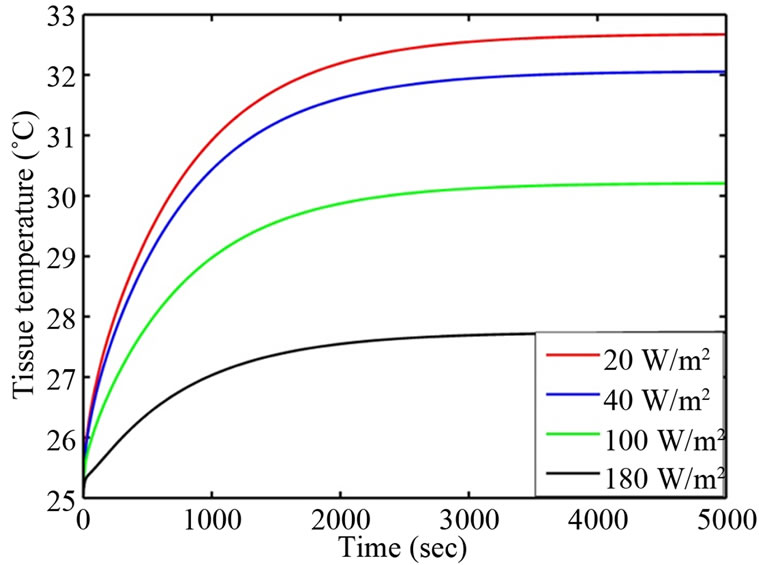
Figure 7. Corneal surface temperature for different evaporation rates (Case II).
For different evaporation rates of 20 W/m2, 40 W/m2, 100 W/m2, 180 W/m2, the corneal surface temperature differences between Case I and Case II are obtained as 0.10˚C, 0.12˚C, 0.18˚C, and 0.27˚C respectively. The differences show that when evaporation rate increases the nodal temperature decreases in both cases but decreasing rate is slow in Case I than Case II. It means, steady state corneal surface temperature is reached earlier in Case I than Case II. This is due to the effect of perfusion and metabolism on retina. The corneal surface temperature is dropped in by 4.78˚C and 4.95˚C in Cases I and II respectively, when evaporation rate is reached from 20 W/m2 to 180 W/m2. Also, steady state corneal temperature is achieved earlier at E = 180 W/m2 than at 20 W/m2. The sudden decrease in corneal temperature at E = 180 W/m2 increases the temperature difference between cornea and aqueous. It is because the greater the temperature difference between two surfaces, the faster is the rate of transfer of thermal energy. Hence steady state corneal temperature is reached earlier at higher evaporation rate.
3.3. Effect of Ambient Temperatures
Heat losses occur due to convection, radiation and tear evaporation at cornea. This loss is strongly related to ambient temperature. In addition, ambient temperature is one of the factors affecting the amount of tear in the eyes [9]. Four sets of ambient temperatures 10˚C, 25˚C, 40˚C, and 50˚C are considered for analysis. The numerical results are presented in Figures 8 and 9.
It can be seen from Figures 8 and 9 that, increase in ambient temperature from 10˚C to 50˚C increases corneal temperature from 27.69˚C to 39.69˚C in Case I and from 27.41˚C to 39.78˚C in Case II. It shows that increase in ambient temperature increases eye temperatures lower in case I compared to Case II and vice versa. This is due to the cooling effect of perfusion at retina. Also, the steady state corneal temperature is reached earlier at T∞ = 10˚C than at T∞ = 50˚C. This is because; more factors are involved in heating eye components than cooling.
3.4. Effect of Lens Thermal Conductivities
It is well known that the water content of lens decreases as age increases. Decrease in water level of lens increases its hardness. This process changes the thermal conductivity of lens due to age [14]. Four sets of values
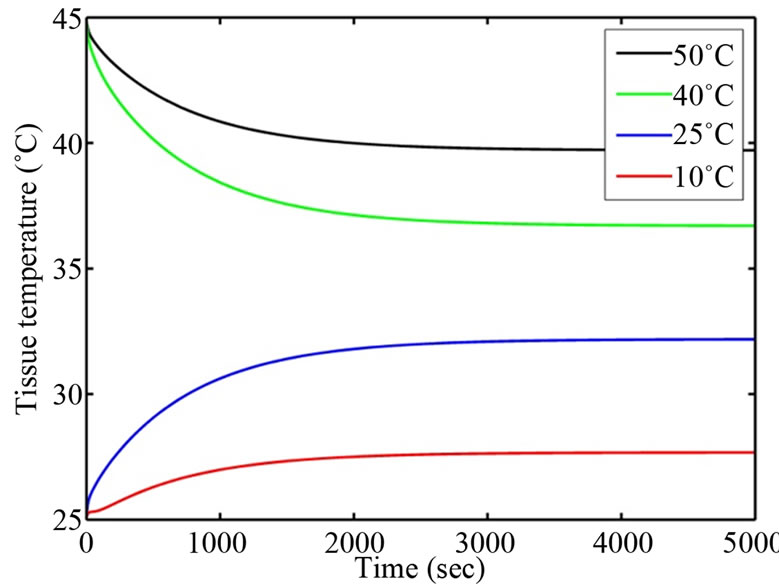
Figure 8. Corneal surface temperature for different ambient temperatures (Case I).
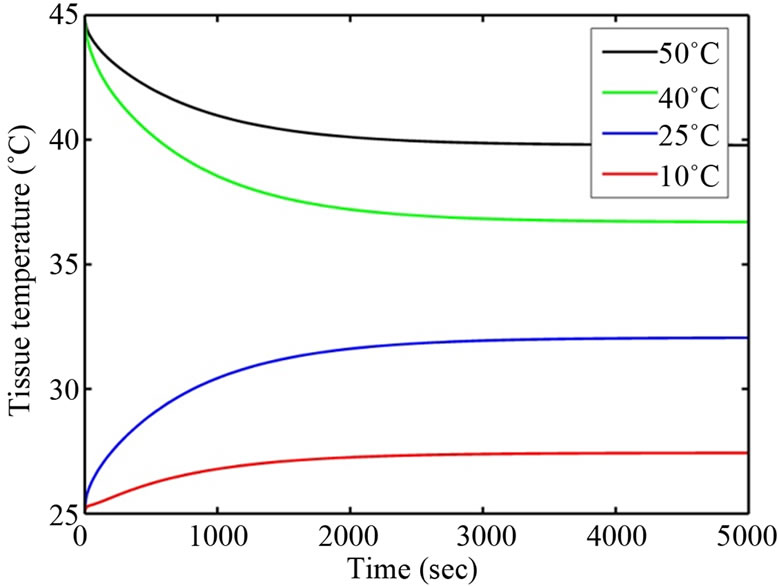
Figure 9. Corneal surface temperature for different ambient temperatures (Case II).
0.21 W/m ˚C, 0.30 W/m ˚C, 0.40 W/m ˚C and 0.54 W/m ˚C are chosen for comparison. The numerical results are presented in Figures 10 and 11.
It is found that, increase in lens thermal conductivity from 0.21 W/m ˚C to 0.54 W/m ˚C increases corneal temperature by 0.87˚C in Case I and by 0.85˚C in Case II but decreases posterior lens temperature by 0.23˚C in Case I and by 0.25˚C in Case II. More heat transfer occurs via conduction from the posterior region to anterior region, when thermal conductivity of lens increases. As a result corneal surface temperature is increased. The steady state corneal temperature is achieved earlier at K3 = 0.54 W/m ˚C than at 0.21 W/m ˚C but the process is reversed in case of posterior part of lens. Similarly, steady state eye temperature is reached earlier in Case I compared to Case II due to the effect of perfusion and metabolism on retina.
4. Conclusions
In this model, a comparative study of temperature distribution with and without considering the effect of blood perfusion and metabolism on retinal part of human eye is
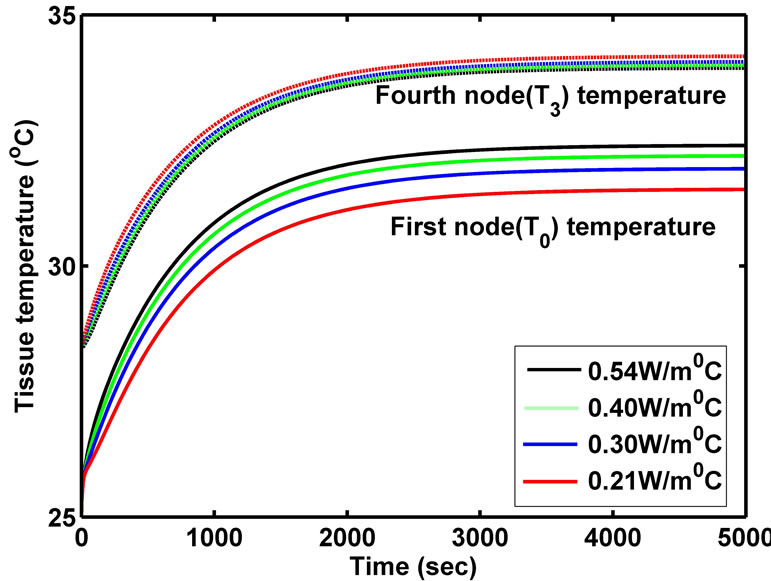
Figure 10. Anterior corneal and posterior lens temperature for different Lens thermal conductivities (Case I).
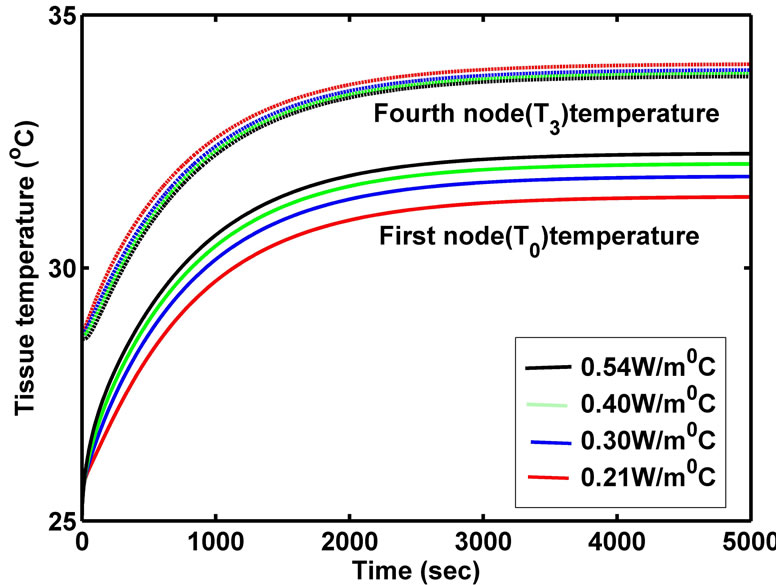
Figure 11. Anterior corneal and posterior lens temperature for different Lens thermal conductivities (Case II).
presented. The steady state corneal temperature is found to be 32.17˚C in Case I and 32.05˚C in Case II respectively. Many authors [1,3,10,13,15] reported similar temperature distribution along the eye pupillary axis. The reported values range from 30.92˚C to 33.7˚C on corneal surface. Hence, our steady state results are in accordance with past results. In earlier studies [1,3,10,13,15], the effect of blood perfusion and metabolism is assumed negligible on retinal part. We are able to show that blood perfusion and metabolism play an important role in maintaining the eye temperature.
The surface temperature of the cornea was measured using bolometer by Mepastone [16], the mean temperature variation on the cornea surface was obtained to be 0.8˚C under 33.2˚C - 36˚C. Kessel et al. [17] found that steady state corneal temperature was achieved between 33˚C to 35˚C, when ambient temperature was increased. Also they found that 20˚C increase in ambient temperature, from 2˚C to 22˚C, was required to increase corneal temperature by 3˚C. In our model, the steady state corneal temperature is achieved between 32.17˚C to 35.58˚C, when ambient temperature is increased from 20˚C to 40˚C. Also, a 20˚C increase in ambient temperature is required to increase corneal temperature by 3.38˚C. Hence, the temperature obtained from our model agrees with the experimental results obtained by Mepastone [16] and Kessel et al. [17]. The slight differences whatsoever obtained may be due to consideration of various parameter values at the layers of human eye.
This model may help to understand the thermal behavior of eye, which can be very crucial in ocular diseases like corneal pain, presbyopia, cataracts etc. This may also prove to be valuable in several eye therapies and surgeries like hyperthermia using microwave, heating due to laser etc. Thus, the model could be useful for the researchers to study the effects of heat flux inside the human eye and medical scientists to improve the diagnosis and treatment.
5. Acknowledgements
The authors would like to thank University Grants commission Nepal for providing financial support to conduct this research work.
REFERENCES
- D. B. Gurung and V. P. Saxena, “Transient Temperature Distribution in Human Dermal Part with Protective Layer at Low Atmospheric Temperature,” International Journal of Biomathematics, Vol. 3, No. 4, 2010, pp. 439-451. http://dx.doi.org/10.1142/S1793524510001070
- V. M. M. Flycket, B. W. Roaymakers and J. J. W. Lagendijk, “Modeling the Impact of Blood Flow on the Temperature Distribution in the Human Eye and the Orbit: Fixed Heat Transfer Coefficient versus the Pennesbioheat Model versus Discrete Blood Vessels,” Physics in Medicine and Biology, Vol. 51, No. 19, 2006, pp. 5007-5021. http://dx.doi.org/10.1088/0031-9155/51/19/018
- T. Wessapan and P. Rattanadecho, “Specific Absorbtion Rate and Temperature Increase in Human Eye Subjected to Electromagnetic Fields at 900 MHZ,” Transactions of the ASME-C-Journal of Heat Transfer, Vol. 134, No. 9, 2012, Article ID: 091101.
- J. Voke, “Occupational Vision Hazards: Infrared Radiation and the Eye,” Optometry Today, Vol. 48, No. 17, 2008, pp. 40-43.
- J. J. W. Lagendijk, “A Mathematical Model to Calculate Temperature Distributions in Human and Rabbit Eyes during Hyperthermia Treatment,” Physics in Medicine and Biology, Vol. 27, No. 11, 1982, pp. 1301-1311. http://dx.doi.org/10.1088/0031-9155/27/11/001
- J. A. Scott, “A Finite Element Model of Heat Transport in the Human Eye,” Physics in Medicine and Biology, Vol. 33, No. 2, 1988, pp. 227-241. http://dx.doi.org/10.1088/0031-9155/33/2/003
- E. H. Amara, “Numerical Investigations on Thermal Effects of Laser-Ocular Media Interaction,” International Journal of Heat and Mass Transfer, Vol. 38, No. 13, 1995, pp. 2479-2488. http://dx.doi.org/10.1016/0017-9310(94)00353-W
- E. Y. K. Ng and E. H. Ooi, “FEM Simulation of the Eye Structure with Bio-Heat Analysis,” Computer Methods and Programs in Biomedicine, Vol. 82, No. 3, 2006, pp. 268-276. http://dx.doi.org/10.1016/j.cmpb.2006.04.001
- E. Li, G. R. Liu, V. Tan and Z. C. He, “Modeling and Simulation of Bioheat Transfer in the Human Eye Using the 3D Alpha Finite Element Method (aFEM),” International Journal for Numerical Methods in Biomedical Engineering, Vol. 26, No. 8, 2010, pp. 955-976.
- M. Cvetkovic, D. Poljak and A. Peratta, “FETD Computation of the Temperature Distribution Induced into a Human Eye by a Pulsed Laser,” Progress in Electromagnetics Research, Vol. 120, 2011, pp. 403-421.
- A. Narasimhan, K. K. Jha and L. Gopal, “Transient Simulations of Heat Transfer in Human Eye Undergoing Laser Surgery,” International Journal of Heat and Mass Transfer, Vol. 53, No. 1, 2009, pp. 482-490. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2009.09.007
- B. Anderson, “Ocular Effects of Changes in Oxygen and Carbon Dioxide Tension,” Transactions of the American Ophthalmological Society, Vol. 66, No. 1, 1968, pp. 423- 474.
- H. H. Pennes, “Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm,” Journal of Applied Physiology, Vol. 85, No. 1, 1998, pp. 5-34.
- K. C. Gokul, D. B. Gurung and P. R. Adhikary, “Effect of Blood Perfusion and Metabolism in Temperature Distribution in Human Eye,” Advances in Applied Mathematical Biosciences, Vol. 4, No. 1, 2013, pp. 13-23.
- H. Wang and Q. H. Qin, “FE Approach with Green’s Function as Internal Trial Function for Simulating Bioheat Transfer in the Human Eye,” Archives of Mechanics, Vol. 62, No. 6, 2010, pp. 493-510.
- R. Mepastone, “Determinants of Corneal Temperature,” British Journal of Ophthalmology, Vol. 52, No. 10, 1968, 729-741. http://dx.doi.org/10.1136/bjo.52.10.729
- L. Kessel, L. Johnson, H. Aridsson and M. Larsen, “The Relationship between Body and Ambient Temperature and Corneal Temperature,” Investigative ophthalmology & Visual Science, Vol. 51, No. 12, 2010, pp. 6593-6597. http://dx.doi.org/10.1167/iovs.10-5659
NOTES
*Corresponding author.

