Applied Mathematics
Vol. 4 No. 9 (2013) , Article ID: 36453 , 9 pages DOI:10.4236/am.2013.49169
Technical Components of Total Factor Productivity Growth in Malaysian Manufacturing Industry
1Faculty of Management and Economics, University of Malaysia Terengganu, Kuala Terengganu, Malaysia
2Graduate School of Business, National University of Malaysia, Bandar Baru Bangi, Malaysia
Email: nhm06@umt.edu.my, nikhaz@ukm.my, ridzuan.yacob@umt.edu.my
Copyright © 2013 Nik Hashim Nik Mustapha et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 9, 2013; revised July 9, 2013; accepted July 16, 2013
Keywords: Total Factor Productivity Growth; Technical Efficiency; Scale Effect; Stochastic Production Frontier
ABSTRACT
This article attempts to disaggregate and explore the components of TFP growth that contribute to changes in output, scale of production, and allocative efficiency and technical efficiency of the Malaysian manufacturing sector. The total factor productivity (TFP) concept defined as total output per unit of all inputs used in the production of an industry has gained a prominent place in academia. The investigation on TFP growth is obviously useful for identifying sources of output growth in the development of an industry. The TFP growth is often interchangeably understood as the technical progress or changes in technology as the sole contributor to economic development. Nonetheless there are other factors contributing to its substance. Knowledge on these technical changes would help decision makers to realize the strengths and weaknesses that contribute to the growth and development of an industry. Alternatively this research would be more beneficial in the case of cross-industry or cross-country comparative studies in order to plan for developmental goal. In such a case a model industry or country can be chosen that exhibits special growth features.
1. Introduction
Growth and development, and later sustainable development had always been in the forefront of attainment goals of world’s economies. Historic attentions were given to multifaceted issues of growth of prominent economic constraints in achieving development objectives. In the oldest profession of agriculture, Robert Maltus [1] first alerted the limitation of food supply because of the growing population leading to surging man-land ratio, which then became the doctrine in food economy. David Ricardo [2] was the first to detect diminishing social well being as a result of rising land rent due to a continued decline of prolific land in cultivation and the dependence of agricultural sector on inferior productivity land. Growth in production of essential food commodities and other agricultural products had taken a turn when potential of land for expansion was constrained by its supply. The ultimate trust of economic growth in production was principally capital while labor was secondary in importance. The significance of human productivity and innovativeness was only recognized during the 1950s and early 1960s following the marvelous contribution of education on economic development [3]. Human development particularly in education, health, nutrition and fertility has since become the focus of most developing nations on the agenda of human resource development and growth. Nowadays, most nations recognize that intellectual capital is essential for sustaining growth as the capacity of human mind, its creativity is limitless and its contribution to innovation is endless. In most cases labor fails to reflect its true influence on the total production for reason that data generally are not available on those skilled and non-skilled workers. Since human capital is an essential ingredient in boosting productivity the World Bank [4] had suggested the use of human-capital adjusted labor (H), which is defined as
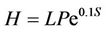
where L is the working-age population, P is the participation rate and S is the number of schooling and e0.1S is a weight used to reflect the impact of education and the size of labor force on the labor input, which is assumed to be exponential. Several findings particularly in Korea suggest that each additional year of schooling raises labor’s productivity by 10 percent. Even though education is relevant to the productivity improvement it will not be so for all situations. With higher education the farmer’s productivity could have declined due to the possibility of better off farm employment. Educated labor tends to be less committed to agriculture and thus its productivity. Experience and on job trainings can be another factor that contribute to higher productivity. Health condition of the workers deteriorates with limitations of medical facilities which in turn impede worker’s productivity. Types of education and trainings that contribute directly to the development of human capital should be differentiated from the ordinary workers. Labor should at least be classified according to skilled and non-skilled labor. No attempt is made in the current study to classify labor according to skilled and non-skilled because of the lack of time series data.
Total factor productivity (TFP) growth is the residual of output growth not accounted for by capital and labor. The derivation of TFP growth components is relevant in order to unveil the unexplained sources of economic growth beyond that reflected in the production function. The residual growth component from the microeconomic perspective can be attributed to technical progress, technical efficiency, scale of firm operation and other socioeconomic factors not captured by the variables used in the production function. In macroeconomics, sources of TFP growth can be categorized into education and training, changes in demand, economic restructuring, technical progress and capital structure [5]. The objective of this paper is to disaggregate TFP growth mathematically from its original definition as suggested by Solow [6]. This article begins with the theoretical development of TFP growth which was extended to the derivation of technical components. The final section deals with TFP growth application using empirical data.
2. Framework for TFP Measurement
The measurement of TFP growth is closely associated with the growth of economic activities. One could not understand TFP growth without first understanding the methodology for estimating growth. The growth concept involves time and its measurement can either be discrete or continuous depending on the extent of pronouncement of the state variables. According to Dowling [7] p. 120, “exponential functions depict constant rates of discrete growth, i.e., growth that takes place at such discrete intervals as at the end of the year or at the end of the quarter.” An example of a discrete growth is given by 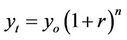 , where yt refers to the current year variable, yo is the base year variable, r is the rate of growth and n is the number of years of the target projection. This discrete growth equation is less pronounced than the continuous growth equation which is represented in natural exponential function such as that of
, where yt refers to the current year variable, yo is the base year variable, r is the rate of growth and n is the number of years of the target projection. This discrete growth equation is less pronounced than the continuous growth equation which is represented in natural exponential function such as that of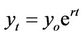 . Throughout this article the discrete growth equation will be used for the estimation of the relevant policy variables in the TFP growth.
. Throughout this article the discrete growth equation will be used for the estimation of the relevant policy variables in the TFP growth.
Theoretical formulation of the TFP growth is based on a simplified production process with only capital (K) and labor (L) utilized as inputs in the production of a commodity, q. Defining q as the product of  and
and 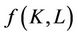 where
where  refers to all influences that go into determining output Q besides capital (machine hours) and labor (labor hours). This mathematical relationship can be presented as
refers to all influences that go into determining output Q besides capital (machine hours) and labor (labor hours). This mathematical relationship can be presented as
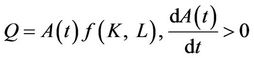 (1)
(1)
The concept of the total factor productivity (TFP) is defined as total output divided by the total inputs. Based on the above simple production function TFP which is 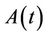 should be equal to total output divided by the total input function
should be equal to total output divided by the total input function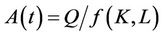 . Assuming that all variables are a function of time, the derivative of output with respect to time yields the following equalities,
. Assuming that all variables are a function of time, the derivative of output with respect to time yields the following equalities,
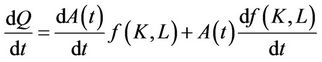 (1.1)
(1.1)
Substitute 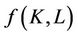 and
and 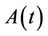 from Equation (1) and expand the derivation of capital and labor with respect to time yields the equation below,
from Equation (1) and expand the derivation of capital and labor with respect to time yields the equation below,
 (1.2)
(1.2)
Dividing through the above equation by Q and setting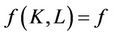 , the output growth equation is obtained as
, the output growth equation is obtained as
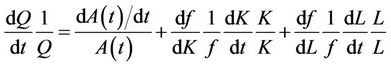 (2)
(2)
As shown in (2) the formulated identities yield the required total output growth that will be used for the estimation of TFP growth. Terms of Equation (2) can be further simplified to arrive at the final result of the output growth equation as in Equation (3)
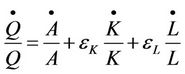 (3)
(3)
where 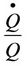 is the total output growth due to technical progress,
is the total output growth due to technical progress, 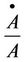 is the total factor productivity growth,
is the total factor productivity growth, 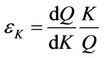 is the output elasticity of capital
is the output elasticity of capital 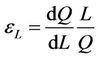 is the output elasticity of labor, while
is the output elasticity of labor, while 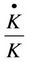 and
and 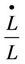 are capital and labor growth rates respectively. The equation for TFP growth is defined as in Equation (4) below
are capital and labor growth rates respectively. The equation for TFP growth is defined as in Equation (4) below
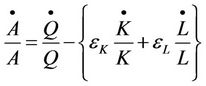 (4)
(4)
3. Disaggregation of TFP Growth
This is one of the techniques whereby TFP and its growth are normally estimated. Obviously there are other techniques; one of which is the Malmquist index as discussed in Coelli [8]. Malmquist index is used to estimate TFP change and to decompose such change into technical change and technical efficiency change using Data Envelopment Analysis (DEA) computer package. The DEA is a special form of linear programming, which comes under operation research and hence it is nonparametric and cannot be tested for validity. In practical applications it is more flexible because DEA is more versatile since it can be easily applied to cases of multiple outputs and inputs. The current study adopts the stochastic frontier production approach that would incorporate technical efficiency change, technical progress and the scale effect as shown in Equation (5). Jesus Felipe [9] asserted that the use of stochastic production frontier makes possible the decomposition of the TPF growth into technical progress and technical efficiency change. The former relates to the shift in the production frontier, that is, the best practices achieved by the industry’s output, and the latter associated with changes attributable to the improvement in managerial practice, workers becoming more skillful through experience and a variety of other reasons that relate to a given technology.
Decomposition of the TFP growth acknowledges the reference of the article written by Rukmani Gounder and Vilaphonh Xayavong [10]. These authors, however, did not show the TFP growth mathematical proof like many articles on the subject. Coelli et al. [11] utilized the production function with the two types of error terms, “Uit” which denotes the technical inefficiency of the industry i in year t, and “Vit” the white noise systematic error term. They are independently and identically distributed with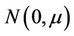 . A higher value of U implies an increase in the technical inefficiency of the industry i and a small value is otherwise. Production function with capital (K) and labor (L) as inputs and the two error terms is presented as
. A higher value of U implies an increase in the technical inefficiency of the industry i and a small value is otherwise. Production function with capital (K) and labor (L) as inputs and the two error terms is presented as
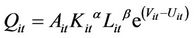 (5)
(5)
 (5.1)
(5.1)
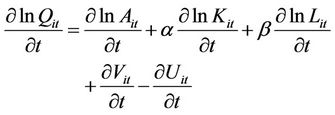 (5.2)
(5.2)
Technical inefficiency (TEit) is further defined as the exponential of negative Uit that is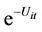 . The rate of technical inefficiency growth is obtained after taking the logarithm of Equation (6.1) and differentiating it with respect to time. The technical inefficiency result is shown in Equation (6.2) which will be used throughout the discussion henceforth. The estimation of technical inefficiency for the manufacturing industry is obtained from the stochastic frontier production function.
. The rate of technical inefficiency growth is obtained after taking the logarithm of Equation (6.1) and differentiating it with respect to time. The technical inefficiency result is shown in Equation (6.2) which will be used throughout the discussion henceforth. The estimation of technical inefficiency for the manufacturing industry is obtained from the stochastic frontier production function.
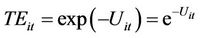 (6.1)
(6.1)
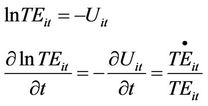 (6.2)
(6.2)
Disregarding it subscripts for the time variables Equation (5.2) is usually presented in its simplified identity as
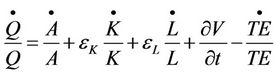 (7)
(7)
TFP growth in actual estimation uses Equation (8) where sK and sL denote the share of capital and labor on production respectively. Substituting Equation (7) into (8) the TFP growth can be further disaggregating into additional components as derived in Equation (9)
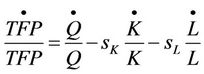 (8)
(8)
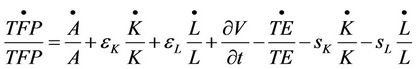 (9)
(9)
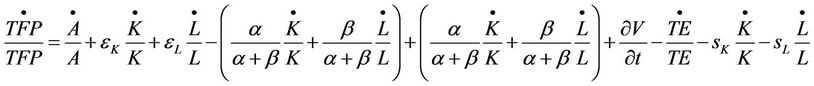 (10)
(10)
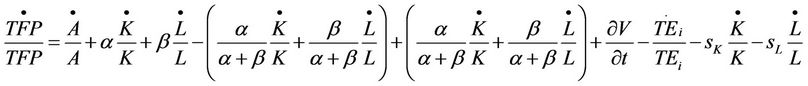 (10.1)
(10.1)
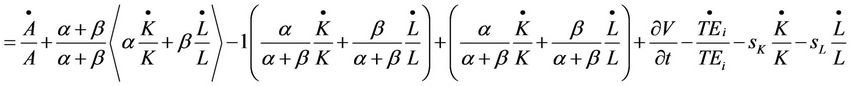 (10.2)
(10.2)
Add 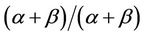 and subtract 1 from equation (10.2) above and with manipulation and rearranging of the terms equations (11.1) and (11.2) are finally arrived at as shown below:
and subtract 1 from equation (10.2) above and with manipulation and rearranging of the terms equations (11.1) and (11.2) are finally arrived at as shown below:
 (11.1)
(11.1)
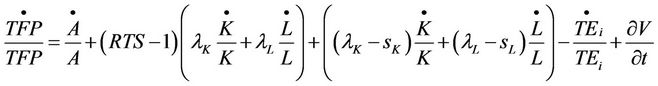 (11.2)
(11.2)
where 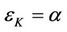 and
and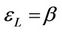 , RTS = return to scale,
, RTS = return to scale,
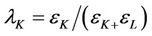 , and
, and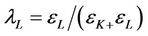 .
. 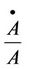 is the technical advancement over time, represented by the shift in the intercept of the production function. This shift can be represented by the time variable but the result of such output may not truly depict the technical progress experienced by an industry or state of a country analyzed.
is the technical advancement over time, represented by the shift in the intercept of the production function. This shift can be represented by the time variable but the result of such output may not truly depict the technical progress experienced by an industry or state of a country analyzed.
Some argued that technical progress is already imbedded in the utilization of physical capital. A technically experienced labor is capable of operating machine to produce a product with precision that saves time, minimizes cost and raises productivity. For computational purpose, further decomposition of the TFP growth Equation (11.2) can be performed by substituting the equivalent of technical progress element as in Equation (4). The final result of TFP growth equation is shown in Equation (12)
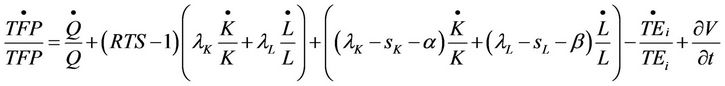 (12)
(12)
Equation (12) is utilized in the final estimation of TFP growth with the help of Excel spreadsheet. Under an optimal production and assuming that the industry operates in a perfectly competitive market the share of capital and share of labor in production are identical to the output elasticity of capital and output elasticity of labor respectively. Defining profit (π) as the difference between total revenue and the total cost, share of labor (sL) and capital (sK) under the assumption of perfect competition should be equivalent to 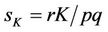 and
and 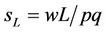 where p is price of output, r and w stand for unit price of capital and labor respectively.
where p is price of output, r and w stand for unit price of capital and labor respectively.
Technical progress (TP) is normally estimated from the effect of time on the total output, which is obtained from the first term on the RHS of Equation (12). The second term following technical progress represents the return to scale level of the industry with respect to changes in capital and labor over time.
Since double logarithmic function is used in the analysis, RTS is equivalent to the sum of capital and labor coefficients which are their respective elasticities. For a sum of elasticity greater than one, the production operates under increasing return to scale (RTS). While a sum of one is a constant RTS and that less than one is decreasing RTS.
This third item represents the allocative efficiency component of the industry since changes in output price and input costs of capital and labor are considered here. The fourth item refers to changes in technical efficiency of the industry. Annual changes in technical efficiency are obtained from the stochastic production frontier using the Cobb-Douglas production function which had included the technical inefficiency variables in the model such as exchange rate, interest rate and the dummy a proxy for impact of outbreak of the financial crisis on the manufacturing sector. Changes in the random error term V refer to the external disturbance not captured in the model. The rest of the notations are as defined above.
4. Growth in Manufacturing Output, Inputs and Productivity
Data for the analysis of manufacturing industry is obtained from Key Indicators of Developing Asian and Pacific Countries, the Economics and Development Resource Center, Asian Development Bank. Since the objective of this paper is to disaggregate the measurement of the TFP growth the principal industries in the manufacturing sector will not be the focus. Instead, the general representation of the industry at two-digit level is presumed sufficient for the illustration needed. The data gathered for the analysis comprise the value of the total output, fixed assets excluding buildings and land, and the number of employed workers for the period 1980 to 2007.
Annual growth in total output, fixed assets, labor and labor productivity, capital productivity and capital-labor ratio for the period 1981-2007 is shown in Table 1. Total output growth was negative for 1985 due to an abrupt decline, after which it showed tremendous improvement for the succeeding years from 1988 through 1995 with the average growth of 9 percent and reached a record high of 10 percent in 1996. Total output growth again experienced a sudden decline of 7 percent in 1997 the year of the monetary crisis followed by a further decline of 7.3 percent in 1998.
Evidently both fixed assets and employed workers had experienced remarkable growth just as did the total output during the late 1980s and the early 1990s. Capital invested in the manufacturing industry grew around 15
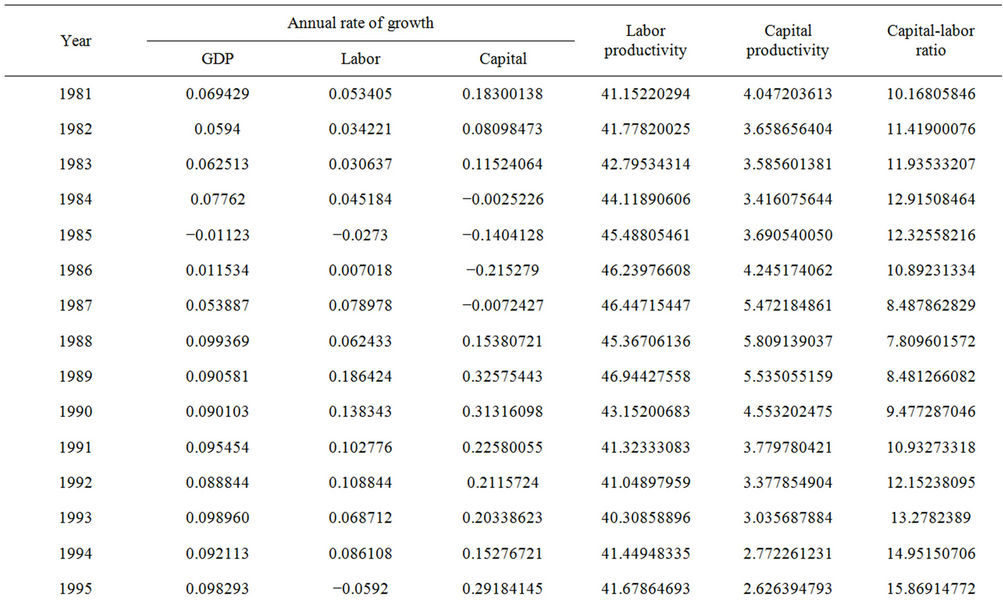
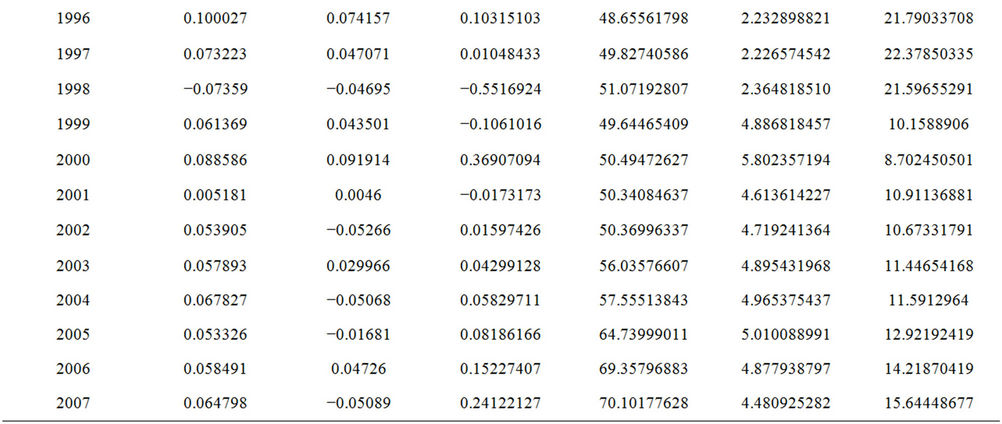
Table 1. Annual rate of growth and productivity for manufacturing industry 1981-2007.
percent to 30 percent annually during the period of 1988- 1995, while the employed workers representing labor grew at much lower percentage for this period. By 1997 growth rates for these factors as expected were negative particularly after the outbreak of economic crisis of 1997 through 1999. Unpredictable fluctuations and volatility in their growth rates appear to follow after this period.
The annual trends in labor productivity, capital productivity and capital-labor ratio for the period 1981 to 2007 are shown in Table 1. A pronounced upward trend in labor productivity was evident starting from 1996 onwards. Labor retrenchment during the economic crisis could have triggered the consequence. Capital productivity has not seemed to improve remarkably and it only took effect moderately after 1999. The growth pattern of labor and capital productivity seemed to have somewhat influenced the trend in capital-labor ratio. Beginning in 1995 the growth in capital-labor ratio had fluctuated upwards reaching its peak during 1996-1998 after which a more gentle fluctuation was observed towards 2007.
5. Manufacturing Total Factor Productivity Growth
With the information on elasticity and the growth rate of inputs, that is capital and labor, one should be able to calculate the TFP and its growth using the formula in Equation (4). Mahadevan [12] utilized production frontier approach to estimate the total factor productivity growth. Coelli et al. [13] utilized time as a variable to segregate the impact of technical progress on total output and attributed the residual as an unexplained growth to the TFP. Alternatively labor can be broken up into several categories of skilled and unskilled labor. Estimates of the change in efficiency for TFP growth are obtained from the stochastic production frontier (SPF). Results of the estimated Cobb-Douglas and Translog stochastic production frontiers (SPF) using 1980-2007 manufacturing industry data are presented in Table 2. The translog function shortcoming is mainly due to loss of the degree of freedom and may not be appropriate for a small number of observations. The maximum likelihood estimate (MLE) technique was applied in both cases using the Frontier 4.1 software.
The inefficiency variables were used in the stochastic production frontiers, namely exchange rate, interest rate and the dummy representing the period economic crisis whereby 1 = crisis year and 0 = otherwise. As evident statistical tests of t-ratios show that the Cobb-Douglas SPF is a better estimator for the manufacturing sector.
The SPF was adopted specifically in this investigation in order to estimate the annual technical efficiency and its annual changes for the TFP growth component. The Cobb-Douglas SPF was chosen for the analysis.
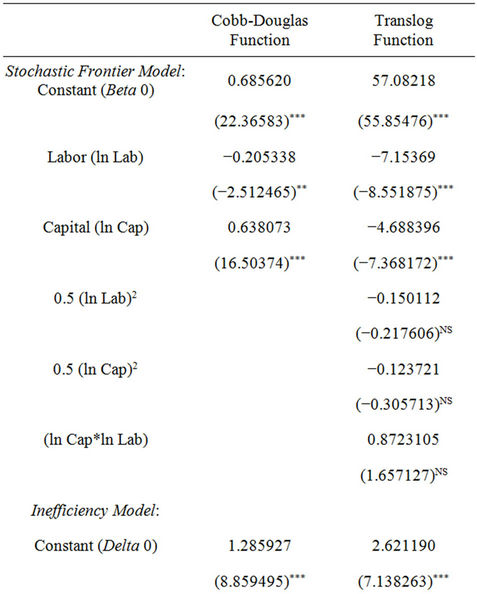
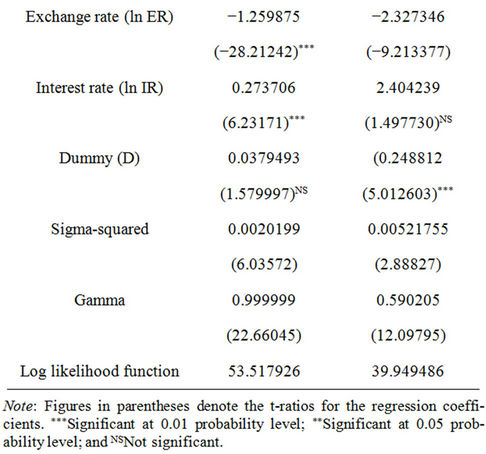
Table 2. Stochastic production frontiers for manufacturing sector 1980-2007.
The annual TFP growth components are shown in Table 3 and their trends are illustrated in Figures 1 and 2 of. The TFP growth components seemed to fluctuate around the zero growth line. One peculiar observation about all the components of TFP growth for the manufacturing is that the downfalls of GDP growth occurred twice during 1981-2007. The first structural break occurred in 1985- 1986 and the second which is more serious during 1997- 1998.
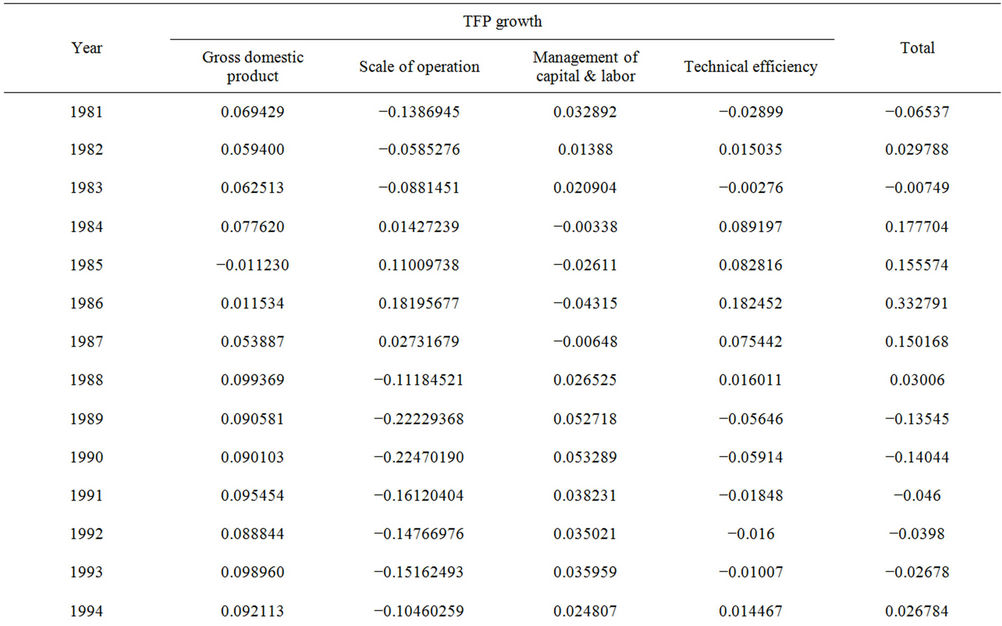
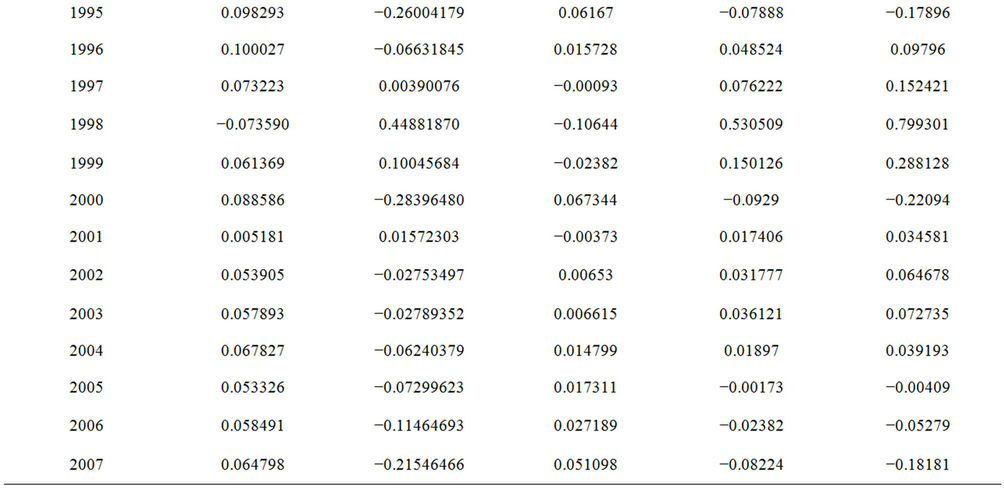
Table 3. Components of total factor productivity growth.
Figure 1 shows that outbreaks of economic crisis which led to downsizing of industrial output resulted in enlargement of industrial scale. This is illustrated in Figure 2 showing the sharp increases in TFP growth of scale operation only during these two periods. During such adjustment period the total output growth and the management of capital and labor as apparent was reduced significantly. Although output growth towards the end of year 2000 was positive it remained relatively low around 5 to 6 percent per annum. However, the industrial technical efficiency had in turn improved as shown in the individual TFP growth components after which it had declined. By the end of the year 2000 growth in technical efficiency continued to register a fall. This pattern had
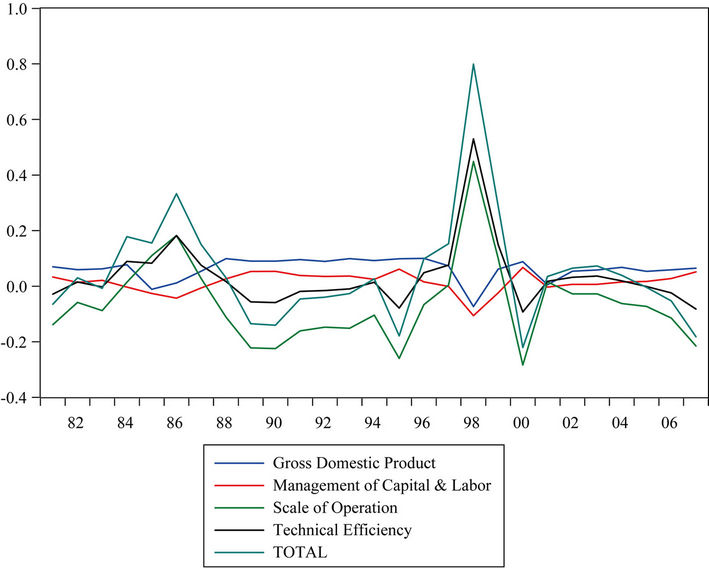
Figure 1. TFP growth for manufacturing 1981-2007.

Figure 2. Components of manufacturing TFP growth.
some impact on the TFP growth.
6. Conclusion
This paper is specifically focused on the methodology of disaggregating the technical components of TFP growth for the manufacturing sector of the Malaysian industry for the period of 1980 to 2007. Since the investigation is centered on the measurement technique limited data was utilized, obtained from the Key Indicators of Developing Asia and Pacific Countries, Asian Development Bank. Methodology for measuring TFP growth is first presented in this investigation. This was followed by the discussion on theoretical development of the TFP growth with the objective of deriving and expanding this simple model to disaggregate TFP growth components. These components comprise the technical progress, industrial return to scale with respect to the use of capital and labor over time, the allocative efficiency given output price and input costs of capital and labor, and changes in technical efficiency of the industry. Finally the stochastic production frontiers (SPFs) were estimated to obtain the necessary parameters from empirical data. It is also emphasized that measuring TFP growth can only be done practically when researchers understand how growth rate is derived and calculated. The discrete growth function is utilized throughout the discussion, as its usage is handy and not easily exploded. The measurement of TFP growth is important from the economic standpoint in order to identify the unexplained contribution to the total output growth other than those explained by capital and labor. This unexplained growth is the technical progress. Nowadays as human resource development is becoming dominant in influencing output growth, intellectual capital besides that of physical capital has been recognized as an essential variable to sustain economic growth. The TFP growth is important for decision makers in identifying sources of technical growth in the private corporation, local government for national planning and for international comparison. Even so the ability to measure and interpret these sophisticated techniques will not be of much use to real world decision making when data sources are insufficient and not reflective of the reality. Thus, the first stage requires data collection and source that is reliable and up to date, while the second stage requires ability to measure and interpret the results obtained from the analyses. As we realize that TFP growth can be estimated by other techniques such as the index numbers, different methods of TFP measurement might produce different results. The estimation technique adopted in this study utilizing the stochastic frontier production with inefficiency model provides a way of estimating TFP growth and component of technical efficiency is probably robust and most appealing currently.
REFERENCES
- D. Ricardo, “Principles of Political Economy and Taxation; Marc Blaug, Economic theory in Retrospect,” 3rd Edition, Cambridge University Press, Cambridge, 1817, pp. 91-112.
- T. Maltus, “An Essay on the Principle of Population as It Affects the Future Improvement of Society,” 1798. Printed for J. Johnson, in St. Paul’s Church-Yard 1998, Electronic Scholarly Publishing Project. http://www.esp.org
- The World Bank, “Poverty and Human Development (Part II),” World Development Report 1980, The International Bank for Reconstruction and Development/The World Bank, Washington D.C., 1980.
- S. R. Ghosh and A. Kraay, “Measuring Growth in Total Productivity,” PREMnote No. 42, The World Bank, 2000.
- National Productivity Corporation, “Productivity Report 2003,” Ministry of International Trade and Industry Malaysia, NPC Selangor, 2004. http://www.npc.org.my
- R. M. Solow, “Technical Change and the Aggregate Production Function,” Review of Economics and Statistics, Vol. 39, No. 3, 1957, pp. 312-320. doi:10.2307/1926047
- E. T. Dowling, “Theory and Problems of Mathematics for Economists,” Schaume’s Outline Series in Economics, McGraw-Hill, Inc., Boston, 1980.
- T. Coelli, “A Guide to DEAP Version 2.1: A Data Envelopment Analysis (Computer) Program,” CEAP Working Paper 96/08. Centre for Efficiency and Productivity Analysis, Deptartment of Econometrics University of New England, Armidale, 1996.
- J. Felipe, “Total Factor Productivity Growth in East Asia: A Critical Survey,” Economics and Development Research Center EDRC Report Series No. 65, 1997.
- R. Gounder and V. Xayavong, “A Decomposition of Total Productivity Growth in New Zealand’s Manufacturing Industries: A Stochastic Frontier Approach,” New Zealand Association of Economic Conference, Wellington, 2004.
- T. Coelli, D. S. P. Rao and G. E. Battese, “An Introduction to Efficiency and Productivity Analysis,” Kluwer Academic Publishers, 1998. doi:10.1007/978-1-4615-5493-6
- R. Mahadevan, “A Frontier Approach to Measuring Total Factor Productivity Growth in Singapore’s Services Sector,” Journal of Economic Studies, Vol. 29, No. 1, pp. 48-58. doi:10.1108/01443580210414111
- T. Coelli, D. S. P. Rao and G. E. Battese, “An Introduction to Efficiency and Productivity Analysis,” Kluwer Academic Publishers, 2003.

