Applied Mathematics
Vol.4 No.10C(2013), Article ID:37493,8 pages DOI:10.4236/am.2013.410A3003
A New Formula for Partitions in a Set of Entities into Empty and Nonempty Subsets, and Its Application to Stochastic and Agent-Based Computational Models
Department of Theoretical Physics, State University of Moldova, Chisinau, Republic of Moldova
Email: fpaladi@usm.md
Copyright © 2013 Ghennadii Gubceac et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 3, 2013; revised July 3, 2013; accepted July 10, 2013
Keywords: Partitions; Agent-Based Models; Stochastic Processes; Complex Systems
ABSTRACT
In combinatorics, a Stirling number of the second kind 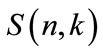 is the number of ways to partition a set of n objects into k nonempty subsets. The empty subsets are also added in the models presented in the article in order to describe properly the absence of the corresponding type i of state in the system, i.e. when its “share”
is the number of ways to partition a set of n objects into k nonempty subsets. The empty subsets are also added in the models presented in the article in order to describe properly the absence of the corresponding type i of state in the system, i.e. when its “share”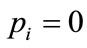 . Accordingly, a new equation for partitions
. Accordingly, a new equation for partitions 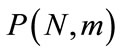 in a set of entities into both empty and nonempty subsets was derived. The indistinguishableness of particles (N identical atoms or molecules) makes only sense within a cluster (subset) with the size
in a set of entities into both empty and nonempty subsets was derived. The indistinguishableness of particles (N identical atoms or molecules) makes only sense within a cluster (subset) with the size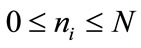 . The first-order phase transition is indeed the case of transitions, for example in the simplest interpretation, from completely liquid state
. The first-order phase transition is indeed the case of transitions, for example in the simplest interpretation, from completely liquid state 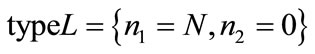 to the completely crystalline state
to the completely crystalline state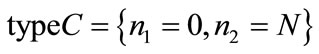 . These partitions are well distinguished from the physical point of view, so they are ‘typed’ differently in the model. Finally, the present developments in the physics of complex systems, in particular the structural relaxation of supercooled liquids and glasses, are discussed by using such stochastic cluster-based models.
. These partitions are well distinguished from the physical point of view, so they are ‘typed’ differently in the model. Finally, the present developments in the physics of complex systems, in particular the structural relaxation of supercooled liquids and glasses, are discussed by using such stochastic cluster-based models.
1. Introduction
In mathematics, particularly in combinatorics and the study of partitions, a Stirling numbers of the second kind count the number of ways to partition a set of n labeled objects into k nonempty unlabelled subsets. By the way, Stirling numbers of the second kind show up more often than those of first and third kind (or Lah numbers), and James Stirling himself considered this kind first [1]. Equivalently, they count the number of different equivalence relations with precisely k equivalence classes that can be defined on an n element set, and they can be calculated using the explicit formula
count the number of ways to partition a set of n labeled objects into k nonempty unlabelled subsets. By the way, Stirling numbers of the second kind show up more often than those of first and third kind (or Lah numbers), and James Stirling himself considered this kind first [1]. Equivalently, they count the number of different equivalence relations with precisely k equivalence classes that can be defined on an n element set, and they can be calculated using the explicit formula , where
, where 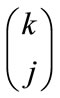 is the binomial coefficient. The sum over the values for k of the Stirling numbers of the second kind, i.e.
is the binomial coefficient. The sum over the values for k of the Stirling numbers of the second kind, i.e.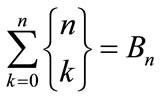 gives the nth Bell number, that is the total number of partitions of a cluster with n entities or agents [2]. The question arises when the empty subsets or clusters are needed to be used in the models, for example, with heterogeneous structure interactions and, subsequently, the partition by Stirling numbers of the second kind becomes inappropriate to count partitions in such complex systems [3].
gives the nth Bell number, that is the total number of partitions of a cluster with n entities or agents [2]. The question arises when the empty subsets or clusters are needed to be used in the models, for example, with heterogeneous structure interactions and, subsequently, the partition by Stirling numbers of the second kind becomes inappropriate to count partitions in such complex systems [3].
In general, agent-based modeling is currently a technique widely used to simulate complex systems in computer science and social sciences. On the other hand, a Markovian process is a stochastic process whose future probabilities are determined by its most recent values. The agent-based computational models (ABM) fits well this description, except for the cases when decisions are dependent on the state of the systems of more than one steps ago, which is the case when ABM agents experience learning, adaptation, and reproduction [4].
In this study, a general equation that describes clustering process among interacting agents in heterogeneous populations, i.e. the partition process in a set of entities into empty and nonempty clusters, is derived and used to study how different behavioral norms affect the individual and social welfare in a population with heterogeneous preferences. One can consider them as an idealization of an imperative and a more liberal approach to social norms or stylized behavioral rules studied by agent-based computational models [5,6]. Another application refers to the generic stochastic model for crystal nucleation which is useful to depict the impact of interface between the nucleus considered as a cluster of a certain number of molecules and the liquid phase for the enhancement of the overall nucleation process. It is generally known that first-order phase transitions occur by nucleation mechanism, and both the nucleus, a cluster of atoms or molecules, and the nucleation work, a energy barrier to the phase transition, are basic thermodynamic quantities in the theory of nucleation. However, the critical nucleus formation is statistically a random event with a probability largely determined by the nucleation work which increases with the subnuclei size [7]. The traditional differential equation modeling is not the alternative to agent-based models; only a set of differential equations, each describing the dynamics of one of the system’s constituent units, is an agent-based model [8].
The general formulation is outlined in Section 2. In Section 3 a probabilistic approach to the crystal nucleation process is considered. The main conclusions are presented in Section 4.
2. The Model
There are N entities which can be in 3 different states (call them left, center and right), and can play 3 actions (again left, center and right). Interaction in this agentbased model involves always one active and one passive player, but agents can play both roles interchangeably. They have preferences over their states: accept one state, are neutral with respect to another state and reject the remaining state. When two agents meet, the active player sets the passive player’s state according to his actionwhich in turn is determined by one of the applied rule. This identifies only 6 possible combinations. Denote with  the shares of the population characterized by each combination of preferences, as in Table 1. That is, drawing randomly one agent, it will be of type i with probability
the shares of the population characterized by each combination of preferences, as in Table 1. That is, drawing randomly one agent, it will be of type i with probability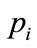 . After each interaction, the passive player gets a payoff of +1 if it is in the accepted state, a payoff of 0 if it is in the neutral state, and a payoff of −1 if it is in the rejected state. The active player does not get any feedback. If the active player follows the first J-rule, it always plays the action corresponding to the accepted state. If it follows the second H-rule, it randomizes between actions corresponding to the accepted and neutral states. The further example will clarify. Suppose two individuals, A and B, meet. Player A is the active one, and rejects left, accepts right, and is thus neutral with respect to the center. Player B is the passive one. It accepts left, rejects right, and is neutral with respect to center, like player A. Suppose A follows the J-rule, and will play right, setting B’s state to right. B will then have a payoff of −1. Suppose, on the other hand, that A follows the H-rule, and will randomize between center and right. The payoff for B could then be either 0 or −1. Note that there is no strategic interaction in the model: the passive player’s payoff depends on the active player’s choice, but the active player’s choice does not depend on the passive player in any way, so the game-theoretic solution concepts like Nash equilibrium become useless.
. After each interaction, the passive player gets a payoff of +1 if it is in the accepted state, a payoff of 0 if it is in the neutral state, and a payoff of −1 if it is in the rejected state. The active player does not get any feedback. If the active player follows the first J-rule, it always plays the action corresponding to the accepted state. If it follows the second H-rule, it randomizes between actions corresponding to the accepted and neutral states. The further example will clarify. Suppose two individuals, A and B, meet. Player A is the active one, and rejects left, accepts right, and is thus neutral with respect to the center. Player B is the passive one. It accepts left, rejects right, and is neutral with respect to center, like player A. Suppose A follows the J-rule, and will play right, setting B’s state to right. B will then have a payoff of −1. Suppose, on the other hand, that A follows the H-rule, and will randomize between center and right. The payoff for B could then be either 0 or −1. Note that there is no strategic interaction in the model: the passive player’s payoff depends on the active player’s choice, but the active player’s choice does not depend on the passive player in any way, so the game-theoretic solution concepts like Nash equilibrium become useless.
Aggregate results are defined in terms of both the mean π and the variance σ2 of the payoffs which denote the stability and the heterogeneity of population, respectively. However, in order to avoid arbitrary choices we do not specify a particular functional form, and report separately the results for the mean and the variance. Let 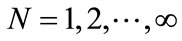 be the total number of entities in the model, and the
be the total number of entities in the model, and the 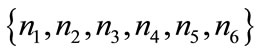 is their partition into
is their partition into 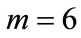 subsets. Each subset can be called cluster, and the process itself—clustering. The size of each cluster can vary from 0 to N,
subsets. Each subset can be called cluster, and the process itself—clustering. The size of each cluster can vary from 0 to N, 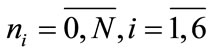 , and
, and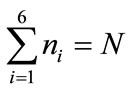 . The number of possible partitions P is a
. The number of possible partitions P is a
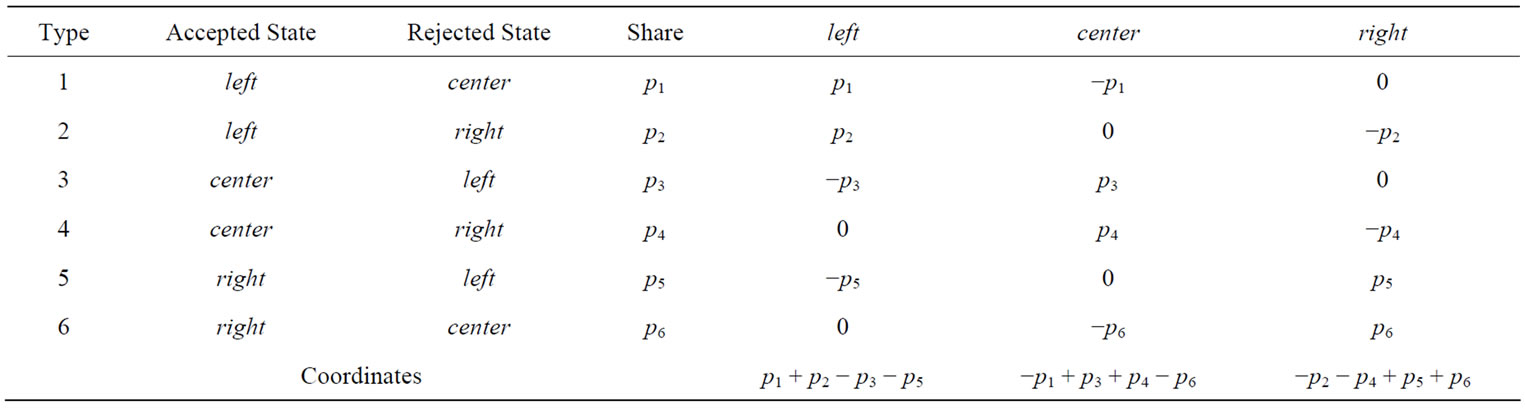
Table 1. Distribution of preferences in the heterogeneous system with 6 types of states.
function of N and m, and the explicit solution is
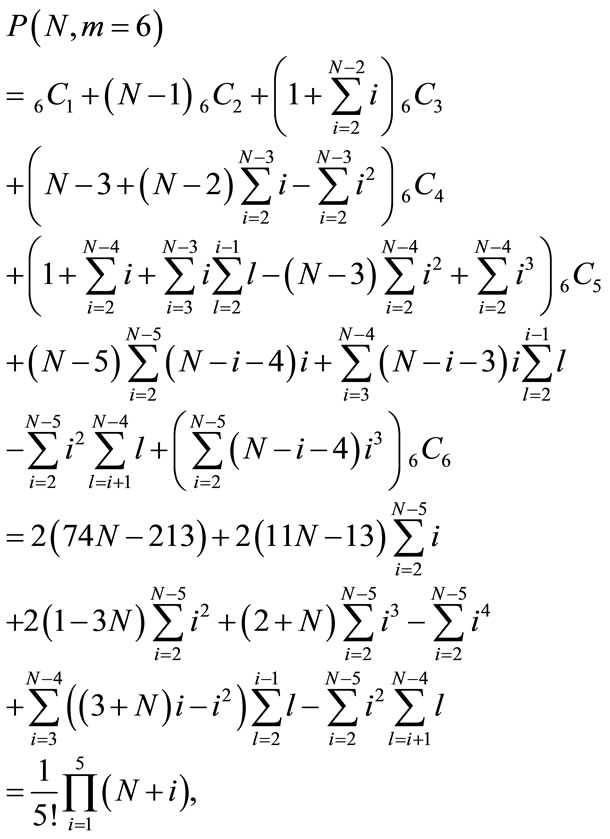
where 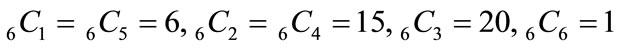 are combinations given by the binomial coefficient
are combinations given by the binomial coefficient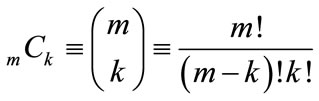 . In general, when the number of subsets
. In general, when the number of subsets , the number of possible partitions P of N agents into m subgroups or subsets is
, the number of possible partitions P of N agents into m subgroups or subsets is
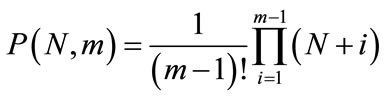 . (1)
. (1)
The matrix is diagonally symmetric

for 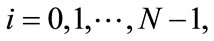 and it can be formed by arranging the partition numbers according to the parameters N and m. Table 2 contains this array of values for the given numbers of partitions. The reccurence relation is
and it can be formed by arranging the partition numbers according to the parameters N and m. Table 2 contains this array of values for the given numbers of partitions. The reccurence relation is
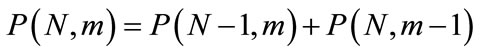
for 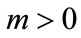 with the initial condition
with the initial condition . For instance, the number 330 in column
. For instance, the number 330 in column  and row
and row 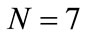 is given by
is given by , where 210 is the number above and 120 is the number on the left of 330. The diagonal elements of the bi-triangular array of values for the numbers of partitions are 1, 2, 6, 20, 70, 252, 924, 3432, 12,870, 48,620, …, and it is represented by nth central binomial coefficient:
, where 210 is the number above and 120 is the number on the left of 330. The diagonal elements of the bi-triangular array of values for the numbers of partitions are 1, 2, 6, 20, 70, 252, 924, 3432, 12,870, 48,620, …, and it is represented by nth central binomial coefficient:
 for all
for all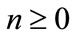 .
.
They are called central since they show up exactly in the middle of the even-numbered rows in Pascal’s traingle. These numbers have the generating function
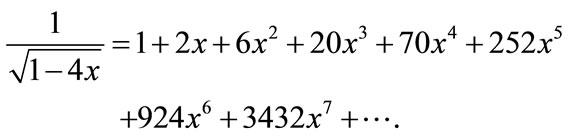
It is known that the asymptotics for the central binomial coefficient 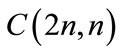 can be written in the form of a particular case of the Wallis formula, i.e.
can be written in the form of a particular case of the Wallis formula, i.e.
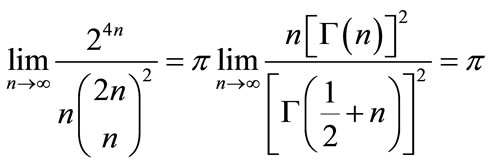 ,
,
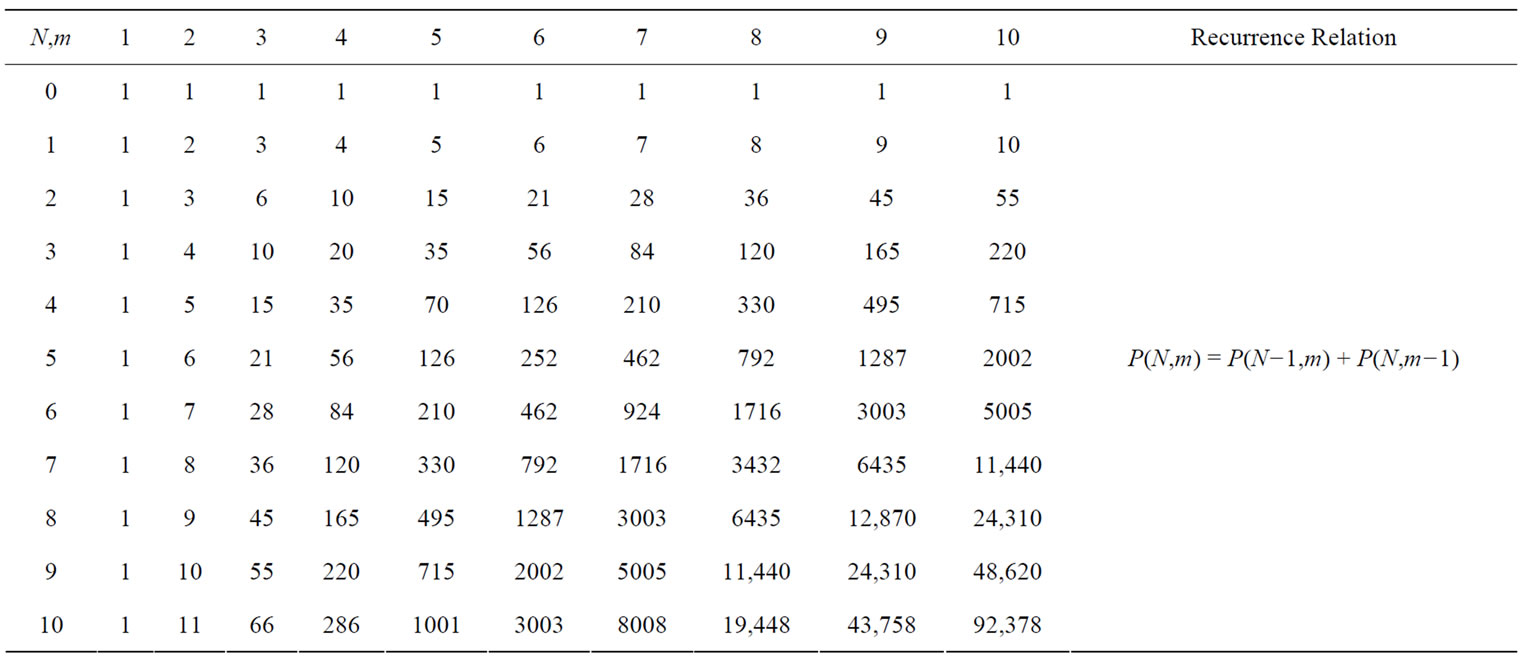
Table 2. Bi-triangular array of values for the numbers of partitions P(N,m).
where 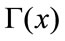 is the gamma function, so
is the gamma function, so
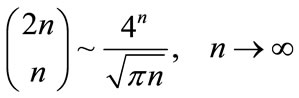 .
.
By the way, this equation can also be used to determine the constant  in front of the Stirling’s formula.
in front of the Stirling’s formula.
Now it is straightforward to see that when all individuals share the same preferences (polarization) the first rule gives a higher payoff. In the other extreme case, when preferences are equally distributed in the ensemble (dispersion) and  it is again straightforward to see that the rules are equivalent, and lead to an average payoff
it is again straightforward to see that the rules are equivalent, and lead to an average payoff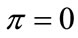 . Consider next an active player of type 1 (accepts left and rejects center) which meets in turn all other (passive) agents, including himself. If it follows the first rule, then it will play left causing a payoff of +1 in
. Consider next an active player of type 1 (accepts left and rejects center) which meets in turn all other (passive) agents, including himself. If it follows the first rule, then it will play left causing a payoff of +1 in 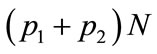 agents, and a payoff of −1 in
agents, and a payoff of −1 in 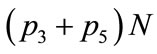 agents. Note that there are
agents. Note that there are  similar entities in the ensemble. Suppose now that everybody meets everybody else both as active and as passive players. Coupling them randomly and randomly choosing active and passive players only adds some noise to the simulation results. So the average payoff when everybody plays according to the first J-rule is
similar entities in the ensemble. Suppose now that everybody meets everybody else both as active and as passive players. Coupling them randomly and randomly choosing active and passive players only adds some noise to the simulation results. So the average payoff when everybody plays according to the first J-rule is
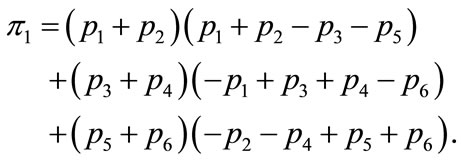 (2)
(2)
Similarly, the average payoff with the second H-rule is
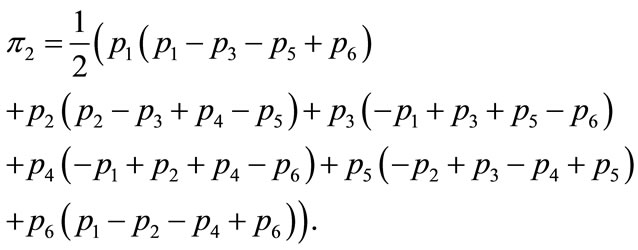 (3)
(3)
To study the behavior of  based on Equations (2) and (3), it is convenient to set some of the probabilities to zero. It is straightforward to see that when there is just one probability different from 0 (and thus equal to 1) we have
based on Equations (2) and (3), it is convenient to set some of the probabilities to zero. It is straightforward to see that when there is just one probability different from 0 (and thus equal to 1) we have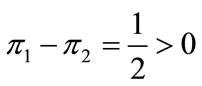 . In general, the number of different possible combinations of non-zero probabilities is given by the above binomial coefficient
. In general, the number of different possible combinations of non-zero probabilities is given by the above binomial coefficient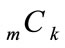 .
.
Thus for two non-zero probabilities we obtain a set of 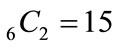 equations which can be grouped in just 3 different functional forms shown in Table 3. Figure 1 graphs these 3 curves for all values of pi and
equations which can be grouped in just 3 different functional forms shown in Table 3. Figure 1 graphs these 3 curves for all values of pi and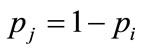 . The J-rule still performs better in all cases but one, when
. The J-rule still performs better in all cases but one, when

Table 3. Expressions of 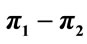 for different numbers of non-zero probabilities pi, i = 1, 2, ···, 6.
for different numbers of non-zero probabilities pi, i = 1, 2, ···, 6.
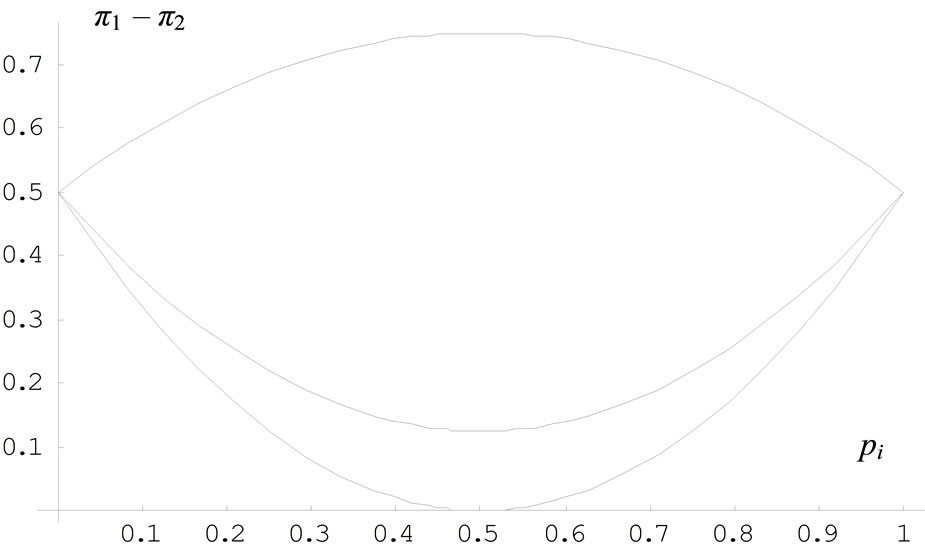
Figure 1.  in the case of two non-zero probabilities, pi and pj = 1 − pi.
in the case of two non-zero probabilities, pi and pj = 1 − pi.
the two rules are equivalent. However, from three nonzero probabilities onward things start to look differently. For three non-zero probabilities we have 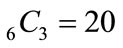 equations, while for four non-zero probabilities there are
equations, while for four non-zero probabilities there are 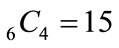 equations, and for five non-zero probabilities
equations, and for five non-zero probabilities  equations. These equations reduce to just three different functional forms in case of three and four nonzero probabilities, and to just one expression in case of five non-zero probabilities.
equations. These equations reduce to just three different functional forms in case of three and four nonzero probabilities, and to just one expression in case of five non-zero probabilities.
A trend towards a better performance of the H-rule, as the distribution of preferences in the system becomes less polarized, is evident. However, in order to better investigate it, a definition of how much preferences are polarized is needed. We represent the distribution of states as a single point in a three dimensional space, where the axes are labeled l, c and r. The l coordinate is found by counting all agents who accept left, and subtracting all agents who reject left. The result is then normalized to the size of the population. Similarly for the other two coordinates. Hence,
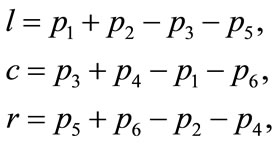 (4)
(4)
where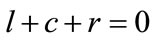 . Note that different distributions of states can lead to the same point in the sphere. For instance, the point in the origin is given not only by
. Note that different distributions of states can lead to the same point in the sphere. For instance, the point in the origin is given not only by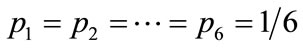 , but by any combination of preferences such as
, but by any combination of preferences such as ,
, 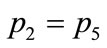 , and
, and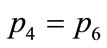 . Taking into account Equation (4), one can define now the polarization of states as the distance from the center of the sphere:
. Taking into account Equation (4), one can define now the polarization of states as the distance from the center of the sphere:
![]() . (5)
. (5)
Note that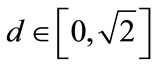 : all points thus lie inside a sphere around the origin.
: all points thus lie inside a sphere around the origin.
The variances 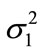 and
and 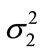 are defined for each discrete distribution
are defined for each discrete distribution  with the expectation (mean) value
with the expectation (mean) value  as follows:
as follows:
 (6.1)
(6.1)
where
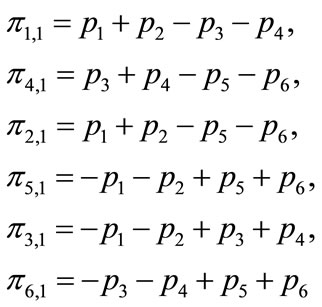 (6.2)
(6.2)
and
 (6.3)
(6.3)
Figure 2 explores how outcomes vary as functions of the distance 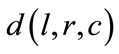 defined by Equation (5). The whole range
defined by Equation (5). The whole range  is sampled, for all probabilities
is sampled, for all probabilities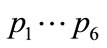 . The step considered for creating all combinations of probabilities is 0.025, i.e. the total number of agents is 40. The average values for
. The step considered for creating all combinations of probabilities is 0.025, i.e. the total number of agents is 40. The average values for 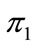 and
and 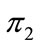 are shown in Figure 2(a), and for each value of the distance from the center of the sphere,
are shown in Figure 2(a), and for each value of the distance from the center of the sphere, 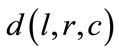 , the frequency of wins with each rule is computed (see Figure 2(b)). When
, the frequency of wins with each rule is computed (see Figure 2(b)). When 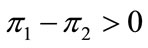 a win is assigned to the first J-rule, and when
a win is assigned to the first J-rule, and when 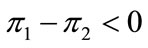 a win is assigned to the second
a win is assigned to the second
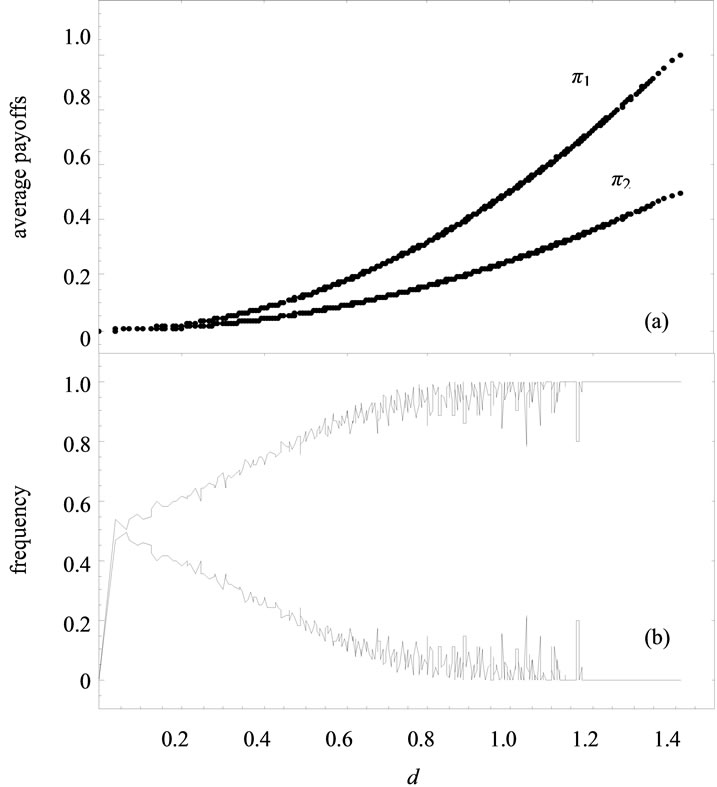
Figure 2. Average values for 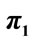 (upper line) and
(upper line) and 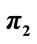 (a), and relative frequency of negative and positive values for
(a), and relative frequency of negative and positive values for  (b) as functions of the distance
(b) as functions of the distance 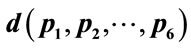 from the center of sphere with a radius of
from the center of sphere with a radius of : 40 entities, 6 clusters in a similar ABM model.
: 40 entities, 6 clusters in a similar ABM model.
one. Exactly in the center of the sphere the two rules lead to the same payoff, independently of the underlying distribution of states. Close to the center, each rule wins in about 50% of the cases. Then, as we move away from the center, the first rule improves its performance, and it is always better when the states are totally polarized, but the total number of states for intermediate values of the distance d is much larger than for the dispersed and polarized states.
Meanwhile, the variance (6.1) with the J-rule (6.2) is generally higher than the variance with the H-rule (6.3), especially when the preferences are dispersed in the system, and when they are quite polarized. On average, however, when one rule is better in terms of higher expected payoffs it is also better in terms of lower heterogeneity, and there are the same average values of the scale-free coefficients of variation on the distance d for any level of fragmentation of states.
3. A Probabilistic Approach to the Crystal Nucleation Process
The second application refers to the nucleation process, a widely spread phenomenon in both nature and technology, which may be considered as a representative of the aggregation phenomena in complex systems. Let’s consider N atoms which can be in 3 different states (cluster, liquid and their interface), and can perform 4 possible moves: liquid to interface, interface to liquid, interface to cluster, and cluster to interface. One can identify 4 different combinations denoted with probabilities , as in Table 4. That is, drawing randomly one particle, it will be of type i with probability
, as in Table 4. That is, drawing randomly one particle, it will be of type i with probability 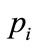 Let
Let  be the total number of atoms in the system, and
be the total number of atoms in the system, and  are their partition into 4 subsets. Each subset can be called cluster, and the number of possible partitions (1) in this case is
are their partition into 4 subsets. Each subset can be called cluster, and the number of possible partitions (1) in this case is
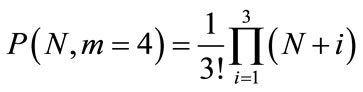 ,
,
where  and
and . For example, in a system of N=1000 atoms,
. For example, in a system of N=1000 atoms,  equals to 167,668,501! Accordingly, the number of repeated computer runs in an ABM model would be very large due to different possible partitions. But we are able to overcome this problem, as already mentioned in the previous section, by developing similar stochastic mathematical models which can describe exactly the results of the agentbased computational models, and, finally, by bridging the gap between ABM modeling and stochastic processes.
equals to 167,668,501! Accordingly, the number of repeated computer runs in an ABM model would be very large due to different possible partitions. But we are able to overcome this problem, as already mentioned in the previous section, by developing similar stochastic mathematical models which can describe exactly the results of the agentbased computational models, and, finally, by bridging the gap between ABM modeling and stochastic processes.
Let’s consider further that each particle interacts with the entire group both as an aggressor in terms of the Kolmogorov mathematical theory [9], and as a passive agent in terms of the ABM computational models as well. Then the mean π, namely the stability index, takes here the form
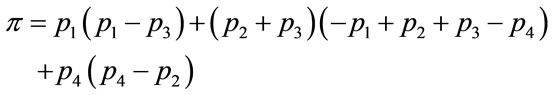 (7.1)
(7.1)
or, taking into account that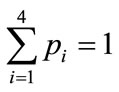 , one can exclude one probability, for example p4, from the above equation:
, one can exclude one probability, for example p4, from the above equation:
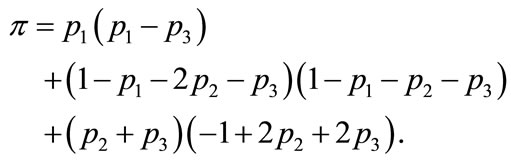 (7.2)
(7.2)
One can represent again the distribution of states as a three-dimensional point  inside a sphere, and the mean payoff π (Equation (7.1) or Equation (7.2)) can be obtained as a function of the distance
inside a sphere, and the mean payoff π (Equation (7.1) or Equation (7.2)) can be obtained as a function of the distance
![]()
where the axes are labeled l, c and 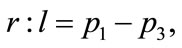
 , and, as stated in the previous section,
, and, as stated in the previous section,  and
and . Thus different distributions of states can lead to the same point in the sphere, i.e. different microscopic partitions can
. Thus different distributions of states can lead to the same point in the sphere, i.e. different microscopic partitions can
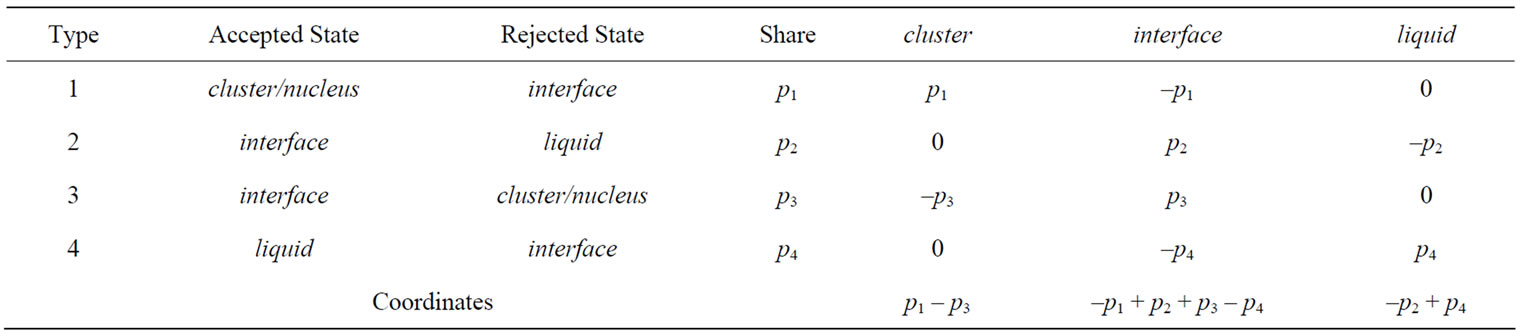
Table 4. Distribution of accepted and rejected states in the system.
generate the same result on aggregate inside a sphere around the origin. The results for the two limit cases are obviously: if all particles would show the same behavior, then 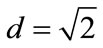 and there is a maximum stability of states in such a completely asymmetrical system, but
and there is a maximum stability of states in such a completely asymmetrical system, but 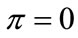 for a homogeneous system,
for a homogeneous system,  , and for combinations such as
, and for combinations such as  and
and 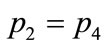 in the case of unstable states.
in the case of unstable states.
4. Conclusions
Mathematical models developed in this paper were used together with agent-based computations to study interactions in two quite different heterogeneous systems. The models are general ones and allow simulations for any size of the system. Our results also support the idea that general properties observed in the complex systems of any kind, which arise from the interplay between random interactions and their complex structures, could be successfully investigated by the same tool. For example, these properties are frequently found in the physical sciences, and are the domain of non-equilibrium statistical mechanics. Because of the real limitations in the use of analytical methods to study such problems, it is often necessary to resort to numerical ones, and the advent of computer simulations has led to an increase of scientific activity in this area that has emerged nowadays as a major subject of interdisciplinary research.
The recent discussions about the gap between agentbased computational models and stochastic analytical models have stimulated the research on this topic [3,10]. In such context, the article supports a unified probabilistic approach to simulation of multi-agent interactions in heterogeneous complex systems. This method appears phenomenological if it is not agent-based, and we prove analytically that the average outcomes of multiple agentbased computations can be described precisely. Furthermore, a useful aggregation procedure for representing the three-dimensional distribution of states, and a general formula that describes clustering process among interacting agents in heterogeneous populations, which is the Equation (1) for partitions in a set of entities into empty and nonempty subsets, are proposed. Bi-triangular array of values for the numbers of partitions is presented, and its diagonal elements are represented by nth central binomial coefficient.
In particular, we obtained that different distributions of states can lead to the same point inside the sphere around the origin, i.e. different microscopic partitions can generate the same aggregate result. It would be a particular conclusion set for the analyzed situations, but one would expect this in different circumstances due to the universal aspects observed in the behavior of complex systems.
5. Acknowledgements
F.P. thanks Dr. Matteo Richiardi for his ABM contribution.
REFERENCES
- R. L. Graham, D. E. Knuth and O. Patashnik, “Concrete Mathematics. A Foundation for Computer Science,” 2nd Edition, Addison-Wesley Professional, Reading, 1994.
- J. Sandor and B. Crstici, “Handbook of Number Theory II,” Kluwer Academic Publishers, Dordrecht, 2004. http://dx.doi.org/10.1007/1-4020-2547-5
- F. Paladi, “On the Probabilistic Approach to Heterogeneous Structure Interactions in Agent-Based Computational Models,” Applied Mathematics and Computation, Vol. 219, No. 24, 2013, pp. 11430-11437. http://dx.doi.org/10.1016/j.amc.2013.05.042
- E. Bonabeau, “Agent-Based Modeling: Methods and Techniques for Simulating Human Systems,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 99, No. 3, 2002, pp. 7280-7287. http://dx.doi.org/10.1073/pnas.082080899
- M. Richiardi and F. Paladi, “Jesus, Hillel and the Man of the Street. Moral and Social Norms in Heterogeneous Populations,” LABORatorio R. Revelli Working Paper 40, 2005. http://eco83.econ.unito.it/terna/swarmfest2005papers/richiardi_paladi.pdf
- M. Richiardi, “Jesus vs Hillel. From Moral to Social Norms and Back,” European Journal of Economic and Social Systems, Vol. 19, No. 2, 2006, pp. 171-190.
- D. Kashchiev, “Nucleation. Basic Theory with Applications,” Butterworth-Heinemann, Oxford, 2000.
- C.W. Gardiner, “Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences,” 2nd Edition, Springer-Verlag, Berlin, 1985.
- A. N. Kolmogorov, “On Statistical Theory of Metal Crystallisation (in Russian),” Izvestiya Academy of Sciences, USSR, Mathematics, Vol. 3, 1937, pp. 355-360.
- L. Feng, B. Li, B. Podobnik, T. Preis and H. E. Stanley, “Linking Agent-Based Models and Stochastic Models of Financial Markets,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 109, No. 22, 2012, pp. 8388-8393. http://dx.doi.org/10.1073/pnas.1205013109

