Received 4 November 2014; revised 2 December 2014; accepted 19 December 2014

ABSTRACT

Through a variable transformation, the Whitham-Broer-Kaup system is transformed into a parameter Levi system. Based on the Lax pair of the parameter Levi system, the N-fold Darboux transformation with multi-parameters is constructed. Then some new explicit solutions for the Whitham-Broer-Kaup system are obtained via the given Darboux transformation.

Keywords:

Whitham-Broer-Kaup Equation, Levi Parameter System, Lax Pair, Darboux Transformation, Soliton Solutions

1. Introduction

Studying of the nonlinear models in shallow water wave is very important, such as Korteweg-de Vries (KdV) equation [1] [2] , Kadomtsev-Petviashvili (KP) equation [3] [4] , Boussinesq equation [5] [6] , etc. There are many methods to study these nonlinear models, such as the inverse scattering transformation [7] , the Bäcklund transformation (BT) [8] , the Hirota bilinear method [9] , the Darboux transformation (DT) [10] , and so on. Among those various approaches, the DT is a useful method to get explicit solutions.

In this paper, we investigate the Whitham-Broer-Kaup (WBK) system [11] -[13] for the dispersive long water in the shallow water

(1)

where is the field of the horizontal velocity, and 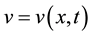is the height that deviates from equilibrium position of the liquid. The constants 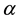and 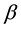represent different diffusion powers. If 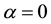and, the WBK system (1) reduces to the classical long-wave system that describes the shallow water wave with diffusion [14] . If 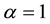and, the WBK system (1) becomes the modified Boussinesq-Burgers equation [7] .

Many solutions have been obtained for the WBK system (1), such as the analytical solution, the soliton-like solution, the soliton solutions, the periodic solution, the rational solution, and so on [15] -[19] .

In this paper, through a proper transformation

(2)

the WBK system (1) is transformed into the parameter Levi system

(3)

Based on the obtained Lax pair, we construct the N-fold DT of the parameter Levi system (3) and then get the N-fold DT of the WBK system (1). Resorting to the obtained DT, we get new multi-soliton solutions of the WBK system.

The paper is organized as follows. In Section 2, we construct the N-fold DT of the Levi system and the WBK system. In Section 3, DT will be applied to generate explicit solutions of the WBK system (1).

2. Darboux Transformation

In this section, we first construct the N-fold DT of the parameter Levi system, and then get explicit solutions of the WBK system.

We consider the following spectral problem corresponding to the Levi system (3)

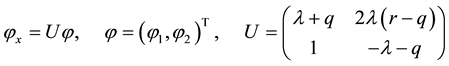(4)

and its auxiliary problem

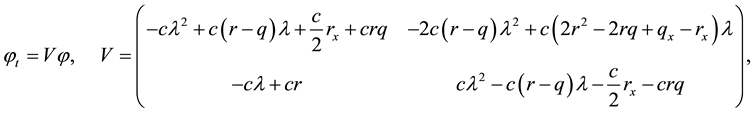(5)

where 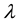is a spectral parameter and. The compatibility condition yields a zero curvature equation which leads to the Levi system (3) by a direct computation.

Now we introduce a transformation of (4) and (5)

, (6)

where is defined by

(7)

Then the Lax pair (4) and (5) are transformed into

(8)

(9)

where, have the same form as, , except replacing, , , with, , , , respectively.

In order to make the Lax pair (4) and (5) invariant under the transformation (6), it is necessary to find a matrix.

Let the matrix in (6) be in the form of

(10)

with

where are functions of and.

Let, be two basic solutions of the spectral problem (4) and use them to define a linear algebraic system

(11)

with

(12)

where the constants, are suitably chosen such that the determinant of the coefficients of (11) are nonzero. If we take

(13)

then are uniquely determined by (11).

From (10), we have

(14)

We note that (11) can be written as a linear algebraic system

(15)

and

,

which implies that are roots of, that is

, (16)

where is independent of. From the above facts, we can prove the following propositions.

Proposition 1. Let satisfy the following first-order differential equation

(17)

Then the matrix determined by Equation (7) is the same form as:

,

where the transformations from the old potentials, to, are given by

(18)

Proof: Let and

, (19)

where denotes the adjoint matrix of. It is easy to see that and are th-order polynomials in, while, are (2N − 1)th-order polynomials in. From (4) and (12), we get

(20)

By using (16) and (20), we can prove that are the roots of. From (15), we have

Hence, together with (19), we have

(21)

that is

(22)

with

where are independent of. By comparing the coefficients of, and in (22), we find

(23)

(24)

(25)

(26)

Substituting (17) into (24)-(26) yields

(27)

From (7) and (22), we find that. The proof is completed.

Remark. When, assuming that, the DT can be rewritten as

(28)

Let the basic solution, of (4) satisfy (5) as well. Through a similar way as Proposition 1, we can prove that has the same form as under the transformation (6) and (18). We get the following proposition.

Proposition 2. Suppose satisfy the following equation

(29)

Then the matrix defined by (9) has the same form as, that is

where and are given by (18).

The proof of Proposition 2 is similar with Proposition 1, but it is much more tedious and then we omit the proof for brevity. For the similar proof we can also refer to [20] [21] .

According to Proposition 1 and 2, the Lax pair (4) and (5) is transformed into the Lax pair (8) and (9), then the transformation (6) and (18): is called the DT of the Lax pair (4) and (5). The Lax pair leads to the parameter Levi system (3) and then the transformation (6) and (18): is also called DT of the parameter Levi system (3). On the other hand, together with the transformation (2), the parameter Levi system (3) is transformed into the WBK system (1), then we get the solutions of the WBK system (1).

Theorem 1. If is a solution of the parameter Levi system (3), with

(30)

is another solution of the parameter Levi system (3), where, , , are determined by (11) and (13).

From the transformation (2), we find that

Theorem 2. If is a solution of the WBK system (1), with

(31)

is another solution of the WBK system (1), where is determined by (30). Then the transformation is also called the DT of the WBK system (1).

3. New Solutions

In this section, we take a trivial solution as the “seed” solution, to obtain multi-soliton solutions of the WBK system (1).

Substituting into the Lax pair (4) and (5), the two basic solutions are

(32)

with,.

According to (12), we get

(33)

For simplicity, we discuss the following two cases, i.e. and.

As, let, solving the linear algebraic system (11) and (13), we have

(34)

according to (28), we get

(35)

Substituting (35) into (31), we obtain the solution of the WBK system (1) as

(36)

with

By choosing proper parameters (such as, , ,), we find that is a bell-type- soliton and is a M-type-soliton.

As, let, together with (11) and (13), we have

(37)

with

With the help of (30), we get

(38)

Then we get another solution of the WBK system (1) by using of (31)

(39)

with

When we take, , , , , , , , is a three- bell-type-soliton solution with two overtaking solitons and one head-on soliton (see Figure 1(a)) and is a three-M-type-soliton solution with two overtaking solitons and one head-on soliton (see Figure 1(b)). We note that by the obtained DT, we can get soliton solutions which are different from those in [19] which are -soliton solutions.

Acknowledgements

This work is supported by Nurture Funds of National Project of University of Shanghai for Science and Technology (no. 14XPQ09).

References