Applied Mathematics
Vol.5 No.1(2014), Article ID:41608,9 pages DOI:10.4236/am.2014.51003
On the Two Methods for Finding 4-Dimensional Duck Solutions
Institute of Administration Engineering, Ltd., Tokyo, Japan
Email: tchizawa@kthree.co.jp
Received February 27, 2013; revised March 27, 2013; accepted April 7, 2013
ABSTRACT
This paper gives the existence of a duck solution in a slow-fast system in R2+2 using two ways. One is an indirect way and the other is a direct way. In the indirect way, the original system is once reduced to the slow-fast system in R2+1. In the direct one, it has a 4-dimensional duck solution when having an efficient local model. This is already published in [1,2]. Some sufficient conditions are given to get such a good model.
Keywords:Slow-Fast System; Singular Perturbation; Duck Solutions; Blowing-Up; Nonstandard Analysis
1. Introduction
In the 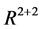 slow-fast system with an invariant manifold, we first assume that this manifold describing limit cycle has a duck solution in a projected
slow-fast system with an invariant manifold, we first assume that this manifold describing limit cycle has a duck solution in a projected  system in
system in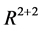 . We introduce 2-dimensional duck solutions in the Section
. We introduce 2-dimensional duck solutions in the Section , then introduce 4-dimensional duck solutions in the Section 4. The blowing up method which constructs a local model
, then introduce 4-dimensional duck solutions in the Section 4. The blowing up method which constructs a local model , is published but revised and extended in this paper, and introduced in the Section
, is published but revised and extended in this paper, and introduced in the Section . In general, we do not need the first assumption to get 4-dimensional duck solutions. It is the shortest way to explain these singular solutions. There are some concrete examples in [3-5].
. In general, we do not need the first assumption to get 4-dimensional duck solutions. It is the shortest way to explain these singular solutions. There are some concrete examples in [3-5].
2. Slow-Fast System in R2
In this section, we shall review some results in Zvonkin and Shubin [6,7]. Let us consider the following system of differential equations
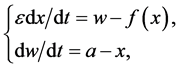 (1)
(1)
where  is defined in
is defined in  and
and  is infinitesimal in the sence of non-standard analysis of Nelson [8]. For the system (1), the graph
is infinitesimal in the sence of non-standard analysis of Nelson [8]. For the system (1), the graph 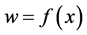 is called the slow curve. We consider the extremum point
is called the slow curve. We consider the extremum point  that separates the attracting part and the repelling part.
that separates the attracting part and the repelling part.
Definition 2.1 A solution 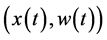 of the system (1) is called a duck solution if there exist standard numbers
of the system (1) is called a duck solution if there exist standard numbers ,
,  ,
, 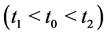
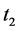 such that 1)
such that 1)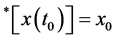 , where
, where ![]() denotes the standard part of
denotes the standard part of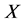 2) for
2) for 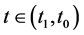 the segment of the trajectory
the segment of the trajectory  is infinitesimally close to the attracting part of the slow curve3) for
is infinitesimally close to the attracting part of the slow curve3) for , it is infinitesimally close to the repelling part of the slow curve, and 4) the attracting and repelling parts of the trajectory are not infinitesimal.
, it is infinitesimally close to the repelling part of the slow curve, and 4) the attracting and repelling parts of the trajectory are not infinitesimal.
We give a necessary condition for the existence of a duck solution close to the extremum point 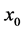 of
of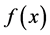 .
.
Proposition 2.2 If there is a duck solution of the system (1) close to the extremum point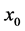 , then
, then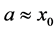 .
.
We finally obtain the following proposition concerning the existence of duck solutions.
Proposition 2.3 Suppose that 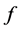 has a nondegenerate extremum point
has a nondegenerate extremum point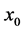 , that is,
, that is, 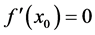 and
and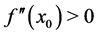 . Then there are the corresponding values of the parameter
. Then there are the corresponding values of the parameter 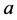 satisfying Proposition 2.2 for which there exist duck solutions in the system (1).
satisfying Proposition 2.2 for which there exist duck solutions in the system (1).
3. Slow-Fast System in R3
We shall introduce 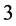 -dimensional duck solutions by E. Benoit to get a concrete image before giving a framework in the
-dimensional duck solutions by E. Benoit to get a concrete image before giving a framework in the  -dimensional duck solutions. Let us consider the following slow-fast system:
-dimensional duck solutions. Let us consider the following slow-fast system:
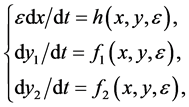 (2)
(2)
where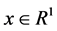 ,
, ![]() , are variables, and
, are variables, and 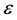 is a parameter as the same as in (1). We give the following assumptions in the system (2).
is a parameter as the same as in (1). We give the following assumptions in the system (2).
(A1) ,
, ![]() are defined on
are defined on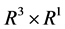 (A2) The set
(A2) The set 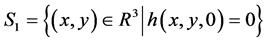 is a
is a 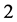 -dimensional differentiable manifold and the set
-dimensional differentiable manifold and the set 
intersects the set  transversely so that the pli set
transversely so that the pli set  is a 1-dimensional differentiable manifold.
is a 1-dimensional differentiable manifold.
(A3)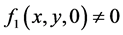 , or
, or 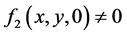 at any point
at any point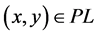 .
.
Let 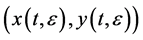 be a solution of (2). When
be a solution of (2). When , differentiating
, differentiating  with respect to the time
with respect to the time , the following equation holds:
, the following equation holds:
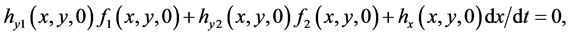
where ,
,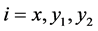 . The above system (2) restricted to
. The above system (2) restricted to 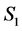 on the neighborhood of
on the neighborhood of 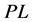 becomes the following system:
becomes the following system:
 (3)
(3)
where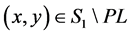 . The system (2) coincides with the system (3) at any point
. The system (2) coincides with the system (3) at any point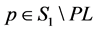 . In order to avoid the degeneracy of the system (3), let us consider the following system:
. In order to avoid the degeneracy of the system (3), let us consider the following system:
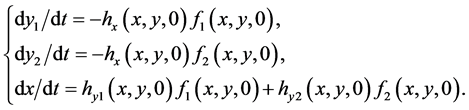 (4)
(4)
As the system (4) is well defined at any point of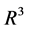 , it is well defined indeed at any point of
, it is well defined indeed at any point of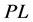 . The solutions of the system (4) coincide with those of the system (3) on
. The solutions of the system (4) coincide with those of the system (3) on 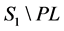 except the velocity when they start from the same initial points.
except the velocity when they start from the same initial points.
(A4) For any point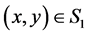 , either of the following holds;
, either of the following holds;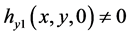 ,
,  , that is, the surface
, that is, the surface  can be expressed as
can be expressed as 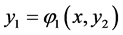 or
or 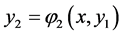 in the neighborhood of
in the neighborhood of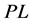 . Let
. Let
 exist, then the projected system (5) is obtained:
exist, then the projected system (5) is obtained:
 (5)
(5)
If we take , it can be analyzed in the same way.
, it can be analyzed in the same way.
(A5) All the singular points of the system (5) are nondegenerate, that is, the matrix induced from the linearized system of (5) at a singular point has distinct nonzero eigenvalues.
Remark All these points are contained in the set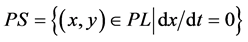 , which is called the set of pseudo singular points. Note that these points are the singular points in the system (4). The above assumptions
, which is called the set of pseudo singular points. Note that these points are the singular points in the system (4). The above assumptions 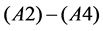 might be enough to use on the neighborhood of these pseudo singular points, because we aim to analyze only in the neighborhood of the pseudo singular point in the system (2).
might be enough to use on the neighborhood of these pseudo singular points, because we aim to analyze only in the neighborhood of the pseudo singular point in the system (2).
Definition 3.1 Let 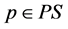 and
and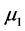 ,
, 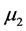 be two eigenvalues of the matrix associated with the linearized system of (5) at
be two eigenvalues of the matrix associated with the linearized system of (5) at . The point
. The point  is called pseudo singular saddle if
is called pseudo singular saddle if  and called pseudo singular node if
and called pseudo singular node if 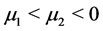 or
or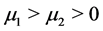 . When
. When ,
,  are complex conjugate, they are called pseudo singular focus.
are complex conjugate, they are called pseudo singular focus.
From now on we use IST [8]. The “transfer principle” is applied for the approximation to the standard analysis. We take the functions , which are non-standard, that is, they depend on
, which are non-standard, that is, they depend on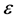 . The second derivative of
. The second derivative of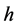 , and the first derivatives of
, and the first derivatives of  have S-continuity. Let the system (2) have a solution
have S-continuity. Let the system (2) have a solution 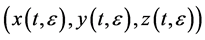 and let
and let 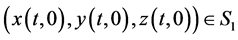 be a solution of the system (4) , then a duck solution is defined as follows.
be a solution of the system (4) , then a duck solution is defined as follows.
Definition 3.2 The solution 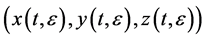 of the systems (2) is called a duck, if there exist standard
of the systems (2) is called a duck, if there exist standard 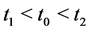 such that 1)
such that 1)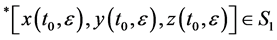 2) for
2) for  the segment of the trajectory
the segment of the trajectory 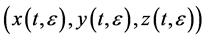 is infinitesimally close to the attracting part of the slow curves (the constrained surface)3) for
is infinitesimally close to the attracting part of the slow curves (the constrained surface)3) for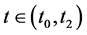 , it is infinitesimally close to the repelling part of the slow curves, and 4) the attracting and repelling parts of the trajectory are not infinitesimal.
, it is infinitesimally close to the repelling part of the slow curves, and 4) the attracting and repelling parts of the trajectory are not infinitesimal.
The definitions of attracting and repelling are the same in [9,10].
Theorem 3.3 (Benoit) If the system has a pseudo singular saddle or node point, then it has duck solutions. In the saddle case, the duck solutions are determined uniquely. In the node case, for the distinct eigenvalues they are determined uniquely, if it has no resonance. If the system has a pseudo singular focus point, it has no duck solutions.
Remark Note that there are some important conditions on the standardness of the functions. At around the pseudo singular point, we blow up the variables in order to get a local model which is described in the Section . In this case, it is determined uniquely. Through the local model, we can get an exact solution as is approximation in the original system. Using transfer principle, we can confirm the existence of 3-dimensional duck solutions. See [9].
. In this case, it is determined uniquely. Through the local model, we can get an exact solution as is approximation in the original system. Using transfer principle, we can confirm the existence of 3-dimensional duck solutions. See [9].
4. Slow-Fast System in R4
Now, let us consider a slow-fast system (6):
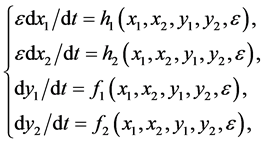 (6)
(6)
where  and
and 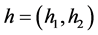 are standard defined on
are standard defined on 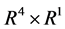 and
and  is infinitesimal.
is infinitesimal.
First, we assume the following condition 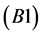 to get an explicit solution.
to get an explicit solution.
(B1) 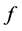 is of class
is of class 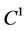 and
and  is of class
is of class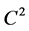 .
.
Furthermore, we assume that the system (6) satisfies the following generic conditions :
:
(B2) The set  is a 2-dimensional differentiable manifold and the set
is a 2-dimensional differentiable manifold and the set 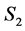 intersects the set
intersects the set , which is a
, which is a 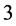 -dimensional differentiable manifold, transversely so that the generalized pli set
-dimensional differentiable manifold, transversely so that the generalized pli set 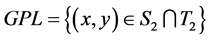 is a
is a  -dimensional differentiable manifold.
-dimensional differentiable manifold.
(B3) The value of 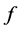 is nonzero at any point
is nonzero at any point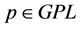 .
.
(B4) The 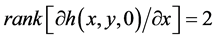 for any
for any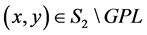 , and the
, and the 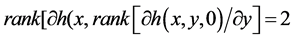
for any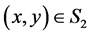 . Then, the surface
. Then, the surface  can be expressed as
can be expressed as 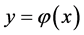 in the neighborhood of
in the neighborhood of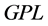 . On the set
. On the set ,
, 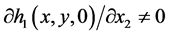 or
or , then
, then  and
and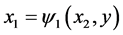 , where we use the notations
, where we use the notations , and
, and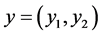 .
.
Assume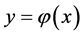 . On the set
. On the set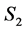 , differentiating both sides of
, differentiating both sides of 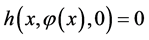 with respect to
with respect to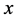 ,
,
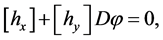 (7)
(7)
where ![]() is a derivative with respect to
is a derivative with respect to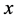 , thus the following is established:
, thus the following is established:
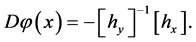 (8)
(8)
On the other hand,

because of . We can reduce the slow system to the following:
. We can reduce the slow system to the following:
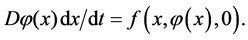 (9)
(9)
Using (8), the system (9) is described by
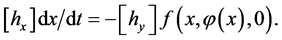
Put 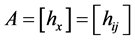 simply, then
simply, then
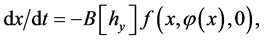 (10)
(10)
where  is a cofactor matrix of
is a cofactor matrix of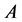 , that is,
, that is, .
. 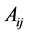 is a cofactor of
is a cofactor of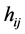 .
.
The system (10) is the time scaled reduced system projected into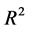 . Again, we assume the set
. Again, we assume the set  .
.
(B5) All the singular points of the system (10) are nondegenerate, that is, the matrix induced from the corresponding linearized system at the singular point has distinct nonzero eigenvalues.
Remark All these points are contained in the set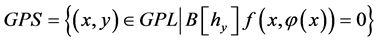 , which is called the set of generalized pseudo singular points.
, which is called the set of generalized pseudo singular points.
As this approach transforms the original system to the time scaled reduced system directly, it is called a direct method.
Definition 4.1 Let 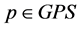 and
and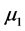 ,
, 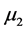 be two eigenvalues of the matrix associated with the linearized system of
be two eigenvalues of the matrix associated with the linearized system of 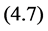 at
at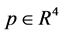 . The point
. The point 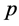 is called generalized pseudo singular saddle if
is called generalized pseudo singular saddle if 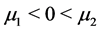 and called generalized pseudo singular node if
and called generalized pseudo singular node if 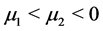 or
or . It is called generalized pseudo singular focus if they are compex conjugate.
. It is called generalized pseudo singular focus if they are compex conjugate.
Now, we have to give a description on the definition of the duck solution in 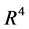 along the direct method. The method induces a
along the direct method. The method induces a 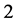 -dimensional projected space directly. Note that we can also once project the original system into a
-dimensional projected space directly. Note that we can also once project the original system into a 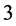 -dimensinal space. It is called the indirect method.
-dimensinal space. It is called the indirect method.
Definition 4.2 Let a point 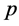 be in GPS. If a trajectory follows first the attractive surface before this point and the saddle point, and then it goes along the slow manifold, which is not infinitesimal, it is called a duck solution in
be in GPS. If a trajectory follows first the attractive surface before this point and the saddle point, and then it goes along the slow manifold, which is not infinitesimal, it is called a duck solution in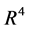 .
.
Furthermore, we assume that the following.
(B6) We assume that there exists the set co-GPL, which may contain GPS and then the transversality condition is also established on co-GPL. In the situation, we assume that the invariant manifold through GPS intersects GPL and co-GPL transversely.
Definition 4.3 If the trajectory near the point of GPS passes through along the slow manifold with not infinitesimal and after that it jumps away, it is called a single duck solution. If there exists a co-GPL in 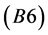 within the interval, it is called a double duck solution.
within the interval, it is called a double duck solution.
Remark The first part of Definition 4.3 ensures that only one of the eigenvalues of the matrix 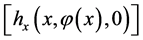 on the slow manifold takes zero on GPS, because the fast vector field has saddle after GPS. On another GPL, however, the other eigenvalue takes zero. Note that these two eigenvalues of
on the slow manifold takes zero on GPS, because the fast vector field has saddle after GPS. On another GPL, however, the other eigenvalue takes zero. Note that these two eigenvalues of  are negative when the fast vector field is attractive, and are positive when it is repulsive. It occurs such a state satisfying the assumption
are negative when the fast vector field is attractive, and are positive when it is repulsive. It occurs such a state satisfying the assumption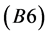 . When they have different sign, it is saddle.
. When they have different sign, it is saddle.
5. Lemmas
In this section, we give two Lemmas to make it clear the structure of the 4-dimensional system and the 3-dimensional projected system.
Let the latter of 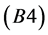 be satisfied, then the following two projected systems (11), (12) in
be satisfied, then the following two projected systems (11), (12) in 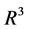 are induced. We assume that
are induced. We assume that  are limited, that is,
are limited, that is, 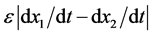 tends to zero as
tends to zero as  tends to zero.
tends to zero.
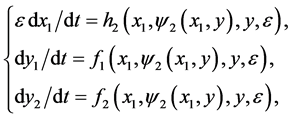 (11)
(11)
since the relation 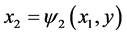 is established from the above assumption. First, we can analyze the vector field of the system (11) on the constrained surface. Then, we use
is established from the above assumption. First, we can analyze the vector field of the system (11) on the constrained surface. Then, we use 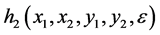 instead of
instead of 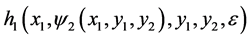 as an approximation. Because we have to avoid redundancy for the system as is using
as an approximation. Because we have to avoid redundancy for the system as is using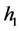 . Actually, we need the above condition:
. Actually, we need the above condition: 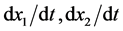 are limited, in such a case. Therefore, this approach is called an indirect method. Using the other relation
are limited, in such a case. Therefore, this approach is called an indirect method. Using the other relation , we can get the following:
, we can get the following:
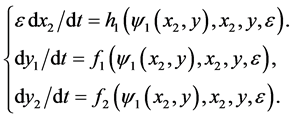 (12)
(12)
Lemma 5.1 The transversality condition 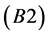 is established if and only if the transversality condition
is established if and only if the transversality condition 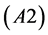 in Section
in Section 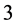 is satisfied in the systems (12) and (11) at the common pseudo singular point.
is satisfied in the systems (12) and (11) at the common pseudo singular point.
Lemma 5.2 The system (11) or (12) have a pseudo singular saddle (or pseudo singular node) point, if the system (6) has a generalized pseudo singular saddle or node point and if the trajectory follows first the attractive surface before this point and saddle or repulsive one after the point having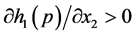 , or
, or 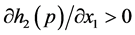 on
on .
.
5.1. Proof of Lemma 5.1
Let 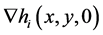 denote a gradient vector of
denote a gradient vector of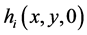 . The transversality between
. The transversality between 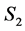 and
and 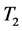 at the generalized pseudo singular point
at the generalized pseudo singular point ![]() is checked as follows:
is checked as follows:
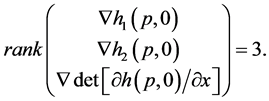 (13)
(13)
The transversality between 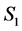 and
and  in the system (11) and (12) are checked as follows. Put
in the system (11) and (12) are checked as follows. Put
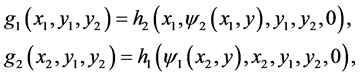
and then put
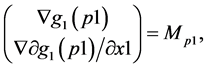 (14)
(14)
where ,
,
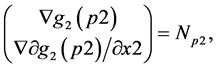 (15)
(15)
As the gradient vectors satisfy the relation (13), 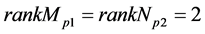 holds. In fact, the gradient vectors in (14) and (15) are independent, since the assumption
holds. In fact, the gradient vectors in (14) and (15) are independent, since the assumption 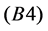 ensures that only the coordinates are changed. Conversely, pulling back the equations (14), (15) to
ensures that only the coordinates are changed. Conversely, pulling back the equations (14), (15) to , that is, embedding the corresponding 2-dimensional manifold into the original
, that is, embedding the corresponding 2-dimensional manifold into the original , we can confirm that the relation (13) holds. In fact, the second equation in (14), (15) is equivalent to the third one in (13). The proof is complete.
, we can confirm that the relation (13) holds. In fact, the second equation in (14), (15) is equivalent to the third one in (13). The proof is complete.
5.2. Proof of Lemma 5.2
Let the original system have a generalized pseudo singular saddle point![]() , that is, the point
, that is, the point  is a singular point of the system (10) satisfying
is a singular point of the system (10) satisfying
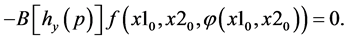
Note that this system is described on the constrained surface.
Now, let us pull it back to the system in . In the case of
. In the case of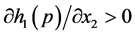 , or
, or , using the assumption
, using the assumption , the following slow-fast system describes the current state.
, the following slow-fast system describes the current state.
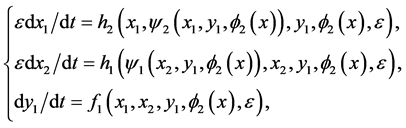 (16)
(16)
and using the assumption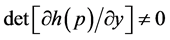 ,
,
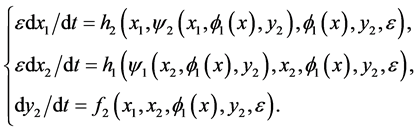 (17)
(17)
The above systems look like having a 1-dimensional slow manifold in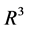 , however, they are tangent each other, because they have a still
, however, they are tangent each other, because they have a still 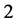 -dimensional differentiable manifold in
-dimensional differentiable manifold in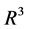 . Therefore, the orbits of the linearized systems (16), (17) are equivalent to the eigenvectors of the time scaled reduced system in the system (10).
. Therefore, the orbits of the linearized systems (16), (17) are equivalent to the eigenvectors of the time scaled reduced system in the system (10).
The condition  on the set
on the set  ensures that the sign of
ensures that the sign of 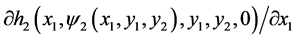 changes
changes  to
to  when one of the eigenvalues in
when one of the eigenvalues in 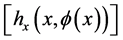 on the slow manifold changes as the same sign. If
on the slow manifold changes as the same sign. If  on the set
on the set  changes the sign, then the value of
changes the sign, then the value of 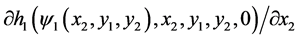 changes in the same way. Therefore, the system (11) has a pseudo singular saddle.
changes in the same way. Therefore, the system (11) has a pseudo singular saddle.
In fact, the system (16) is equivalent to the system (11) and the system (17) is also equal to the system (12). In the case of the node point, the proof is similar. The proof is complete.
6. Local Models
In this section, we shall give the following two theorems through a local model in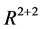 . See [1].
. See [1].
Theorem 6.1 Let 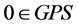 be saddle or node. If the matrix
be saddle or node. If the matrix 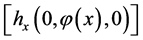 has one zero eigenvalue and the other one has negative with a local model satisfying the conditions:
has one zero eigenvalue and the other one has negative with a local model satisfying the conditions: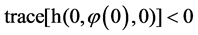
 ,
,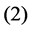
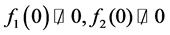 , there exists a duck solution in
, there exists a duck solution in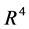 .
.
(Proof) As only one of the eigenvalues of the matrix 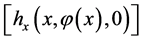 on the slow manifold takes zero on GPS, the assumptions
on the slow manifold takes zero on GPS, the assumptions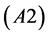 ,
,  ensure that two eigenvalues of
ensure that two eigenvalues of 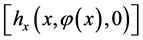 are negative in the fast vector field before GPS. They are maybe negative, respectively positive after GPS. When each coefficient on GPS is limitted, a local model shows a precise structure as an approximation of the original system. Then, the property on GPS reflects directly the whole system. It can be shown that the time scaled reduced system
are negative in the fast vector field before GPS. They are maybe negative, respectively positive after GPS. When each coefficient on GPS is limitted, a local model shows a precise structure as an approximation of the original system. Then, the property on GPS reflects directly the whole system. It can be shown that the time scaled reduced system  is an apprximated one with a singular solution of the whole system
is an apprximated one with a singular solution of the whole system , because the corresponding solutions are very close to each other under the only two conditions. Therefore, we can conclude that there exists a duck solution.
, because the corresponding solutions are very close to each other under the only two conditions. Therefore, we can conclude that there exists a duck solution.
Let  be saddle or node. When changing the variables correspond to microscopes
be saddle or node. When changing the variables correspond to microscopes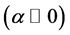 :
: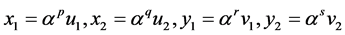 ,
,  , the original system is reduced to the system with variables
, the original system is reduced to the system with variables ,
,  ,
,  ,
,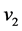 . Then there exist local models which describe the
. Then there exist local models which describe the 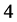 -dimensional duck solutions.
-dimensional duck solutions.
Theorem 6.2 If the system has a square-linear solution in a local model, for any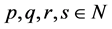 , there exist essentially two local models describing the explicit duck solutions.
, there exist essentially two local models describing the explicit duck solutions.
(Proof)
In the case ,
, 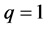 ,
,  ,
, 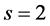 , changing variables:
, changing variables:
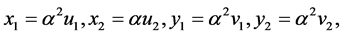 (18)
(18)
we reduce the system as well in (19) as well in (20).
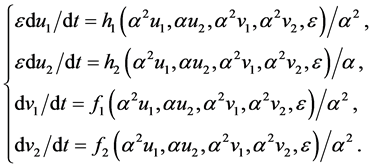 (19)
(19)
Multiplying the right hand side of the system (19) by ,
,
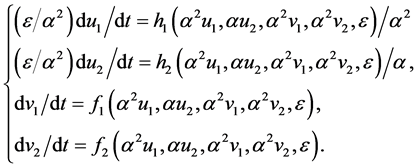 (20)
(20)
In fact, doing time scaling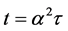 , then
, then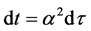 . It is easy to show that Formula (20) is equivalent to (19).
. It is easy to show that Formula (20) is equivalent to (19).
By using the assumptions  and
and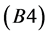 , we construct a local model under the most simple conditions:
, we construct a local model under the most simple conditions:
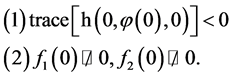 (21)
(21)
Putting  infinitesimal to δ simply, that is δ = L(ε3)
infinitesimal to δ simply, that is δ = L(ε3)
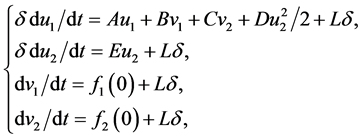 (22)
(22)
where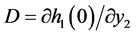
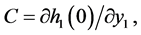

 ,
,![]() ,
,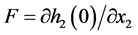 .
.
Note that the conditions 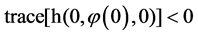 imply that
imply that  is saddle. See Definition 4.3. The corresponding solutions in the local model are as follows: when
is saddle. See Definition 4.3. The corresponding solutions in the local model are as follows: when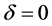 ,
,
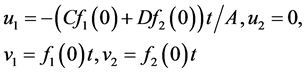 (23)
(23)
when ,
,
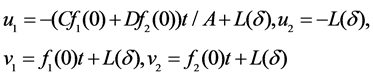 (24)
(24)
In the case ,
, 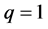 ,
, 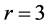 ,
, 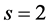 , changing variables:
, changing variables:
 (25)
(25)
we construct a local model under the conditions:
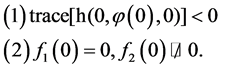 (26)
(26)
The corresponding local model is
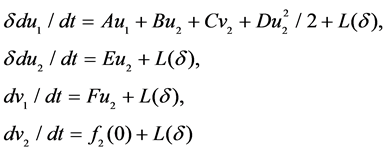 (27)
(27)
where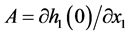 ,
,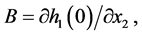
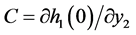 ,
,![]() ,
,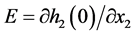 ,
, .
.
Notice that we assume again that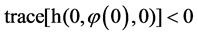 , because the fast vector field has one zero eigenvalue and the other one is negative. The corresponding solutions in the local model are as follows: when
, because the fast vector field has one zero eigenvalue and the other one is negative. The corresponding solutions in the local model are as follows: when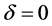 ,
,
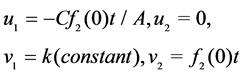 (28)
(28)
when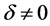 ,
,
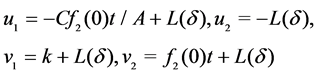 (29)
(29)
In another case, it is impossible to get an explicit solution with a square-linear one but a cubic-linear (or much higher order) one.
In this approach, an invertible affine transformation must be needed for a general point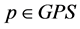 , because the conditions (21), (26) are assumed at only
, because the conditions (21), (26) are assumed at only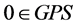 . These conditions may not be satisfied at the general pseudo singular point. We have to change the coordinates from the point
. These conditions may not be satisfied at the general pseudo singular point. We have to change the coordinates from the point 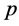 to
to . Notice that we do not know if the corresponding affine transformation keeps the conditions (21). In many cases, however, it is feasible.
. Notice that we do not know if the corresponding affine transformation keeps the conditions (21). In many cases, however, it is feasible.
7. Remark
It is easy to find that any solutions 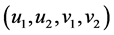 at the same time
at the same time 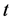 in (23) and (24) are very near. This fact implies that the time scaled reduced system is an approximated one. As blowing up the coordinates, the microscopes give a freedom on the solutions with respect to the initial values. The corresponding local model has higher possible polynomial solutions (not to be unique generally). We choose the smallest polynomial order.
in (23) and (24) are very near. This fact implies that the time scaled reduced system is an approximated one. As blowing up the coordinates, the microscopes give a freedom on the solutions with respect to the initial values. The corresponding local model has higher possible polynomial solutions (not to be unique generally). We choose the smallest polynomial order.
Acknowledgements
We would thank I. V. D. Berg who read through our preprint carefully and gave many suggestions to make it better. H. Nishino and Dr student H. Miki gave us valuable comments especially in the Section 6.
REFERENCES
- K. Tchizawa, “On a Local Model for Finding 4-Dim Duck Solutions,” Selected Topics in Mathematical Methods and Computational Techniques in Electrical Engineering, WSEAS Press, 2010, pp. 177-183.
- K. Tchizawa, “On Relative Stability in 4-Dimensional Duck Solutions,” Journal of Mathematics and System Science, Vol. 2, No. 9, 2012, pp. 558-563.
- K. Tchizawa and S. A. Campbell, “On Winding Duck Solutions in R4,” Proceedings of Neural, Parallel, and Scientific Computations, Vol. 2, 2002, pp. 315-318.
- S. A. Campbell and M. Waite, “Multistability in Coupled Fitzhugh-Nagumo Oscillators” Nonlinear Analysis, Vol. 47, No. 2, 2000, pp. 1093-1104. http://dx.doi.org/10.1016/S0362-546X(01)00249-8
- H. Miki, H. Nishino and K. Tchizawa, “On the Possible Occurrence of Duck Solutions in Domestic and Two-Region Business Cycle Models,” Nonlinear Studies, Vol. 19, No. 1, 2012, pp. 39-55.
- F. Diener and M. Diener, “Nonstandard Analysis in Practice,” Springer-Verlag, Berlin, 1995.
- A. K. Zvonkin and M. A. Shubin, “Non-Standard Analysis and Singular Perturbations of Ordinary Differential Equations,” Russian Mathematical Surveys, Vol. 39, No. 2, 1984, pp. 69-131. http://dx.doi.org/10.1070/RM1984v039n02ABEH003091
- E. Nelson, “Internal Set Theory,” Bulletin of the American Mathematical Society, Vol. 83, No. 6, 1977, pp. 1165-1198. http://dx.doi.org/10.1090/S0002-9904-1977-14398-X
- E. Benoit, “Canards et Enlacements,” Publications Mathématiques de l’IHÉS, Vol. 72, No. 1, 1990, pp. 63-91. http://dx.doi.org/10.1007/BF02699131
- E. Benoit, “Canards en un Point Pseudo-Singulier Noeud,” Bulletin de la Société Mathématique de France, 1999, pp. 2-12.

