Applied Mathematics
Vol. 4 No. 5 (2013) , Article ID: 31225 , 16 pages DOI:10.4236/am.2013.45104
Characterizations of Hemirings by the Properties of Their k-Ideals
Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
Email: mshabirbhatti@yahoo.co.uk
Copyright © 2013 Muhammad Shabir, Rukhshanda Anjum. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 26, 2012; revised March 22, 2013; accepted March 30, 2013
Keywords: Hemiring; Fuzzy k-Ideal; Idempotent k-Ideals; Prime Ideals; Semiprime Ideals
ABSTRACT
In this paper we characterize those hemirings for which each k-ideal is idempotent. We also characterize those hemirings for which each fuzzy k-ideal is idempotent. The space of prime k-ideals (fuzzy k-prime k-ideals) is topologized.
1. Introduction
The notion of semiring, introduced by H. S. Vandiver in 1934 [1] is a common generalization of rings and distributive lattices. Semirings play an important role in the development of automata theory, formal languages, optimization theory and other branches of applied mathematics (see for example [2-8]). Hemirings, which are semirings with commutative addition and zero element are also very important in theoretical computer science (see for instance [3,6,7]). Some other applications of semirings with references can be found in [5-7,9]. On the other hand, the notions of automata and formal languages have been generalized and extensively studied in a fuzzy frame work (cf. [8-10]).
Ideals play an important role in the structure theory of hemirings and are useful for many purposes. But they do not coincide with usual ring ideals. For this reason many results in ring theory have no analogues in semirings using only ideals. Henriksen defined in [11] a more restricted class of ideals in semirings, which is called the class of k-ideals. These ideals have the property that if the semiring R is a ring then a subset of R is a k-ideal if and only if it is a ring ideal. Another class of ideals is defined by Iizuka [12], which is called the class of h-ideals. In [13] La Torre studied these ideals, thoroughly.
The concept of fuzzy set was introduced by Zadeh in 1965 [14]. Many researchers used this concept to generalized different notions of algebra. Fuzzy semirings were first studied by Ahsan et al. [15] (see also [16]). Fuzzy k-ideals are studied in [17-22]. Fuzzy h-ideals are studied in [23-29]. In this paper we characterize those hemirnigs for which each k-ideal is idempotent and also those hemirings for which each fuzzy k-ideal is idempotent. The rest of this is organized as follows.
In Section 2, we summarize some basic concepts which will be use throughout this paper; these concepts are related to hemirings and fuzzy sets. In Section 3, k-product and k-sum of fuzzy sets in a hemiring are given. It is shown that k-product (k-sum) of fuzzy k-ideals of a hemiring is a k-ideal. Characterization of k-hemiregular hemiring in terms of fuzzy left k-ideal and fuzzy right k-ideal is also given in this section. Section 4 is about idempotent fuzzy k-ideals of a hemiring. Different characterization of hemirings in which each fuzzy k-ideal is idempotent is given. In Sections 5 and 6, prime, semiprime, irreducible fuzzy k-ideals are studied. In last section, the space of prime k-ideals (fuzzy k-prime k-ideals) is topologized.
2. Basic Results on Hemirings
A semiring is an algebraic system  consisting of a non-empty set R together with two binary operations called addition “+” and multiplication “·” such that
consisting of a non-empty set R together with two binary operations called addition “+” and multiplication “·” such that 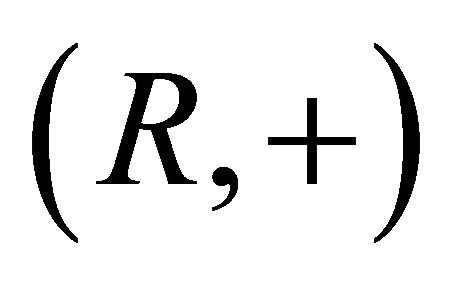 and
and 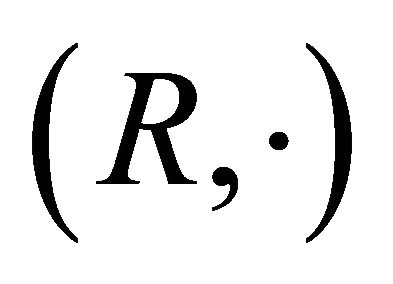 are semigroups and connecting the two algebraic structures are the distributive laws:
are semigroups and connecting the two algebraic structures are the distributive laws:

for all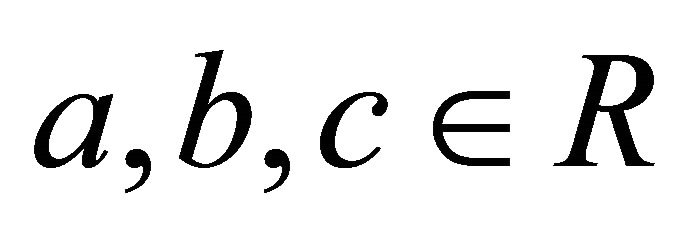 .
.
A semiring 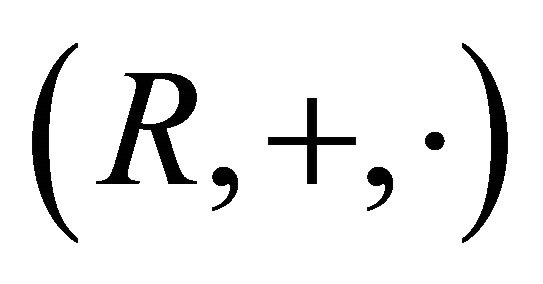 is called a hemiring if “+” is commutative and
is called a hemiring if “+” is commutative and 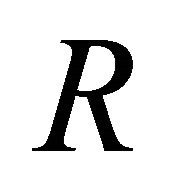 has a zero element 0, such that
has a zero element 0, such that 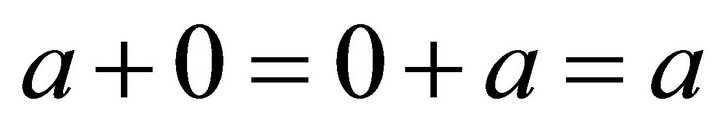 and
and 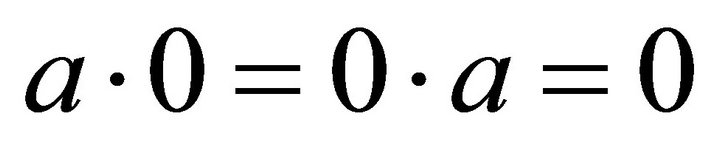 for all
for all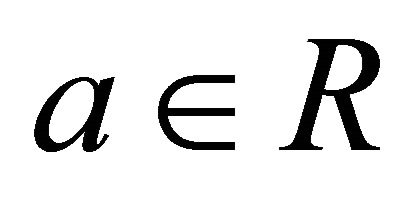 . An element
. An element  (if it exists) is called an identity element of
(if it exists) is called an identity element of 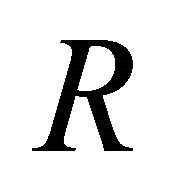 if
if  for all
for all . If a hemiring contains an identity element then it is called a hemiring with identity. A hemiring
. If a hemiring contains an identity element then it is called a hemiring with identity. A hemiring  is called a commutative hemiring if “
is called a commutative hemiring if “ ” is commutative in R.
” is commutative in R.
A non-empty subset A of a hemiring R is called a subhemiring of R if A itself is a hemiring with respect to the induced operations of R. A non-empty subset I of a hemiring R is called a left (right) ideal of R if 1)  for all
for all 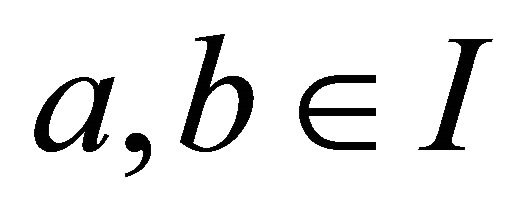 and 2)
and 2) 
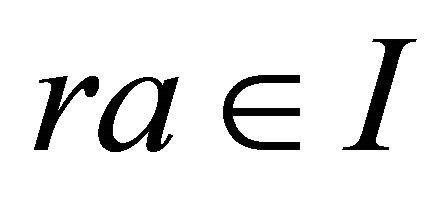 for all
for all ,
, . Obviously
. Obviously  for any left (right) ideal I of R. A non-empty subset I of a hemiring R is called an ideal of R if it is both a left and a right ideal of R. A left (right) ideal I of a hemiring R is called a left (right) k-ideal of R if for any
for any left (right) ideal I of R. A non-empty subset I of a hemiring R is called an ideal of R if it is both a left and a right ideal of R. A left (right) ideal I of a hemiring R is called a left (right) k-ideal of R if for any 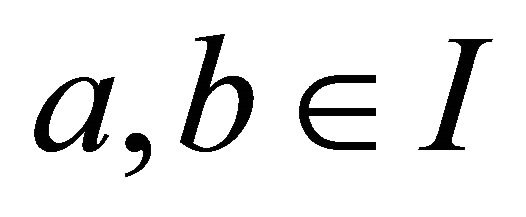 and
and 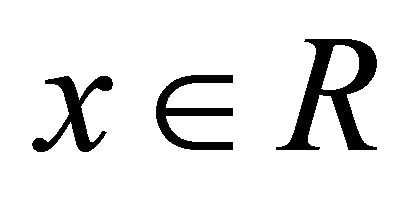 from
from 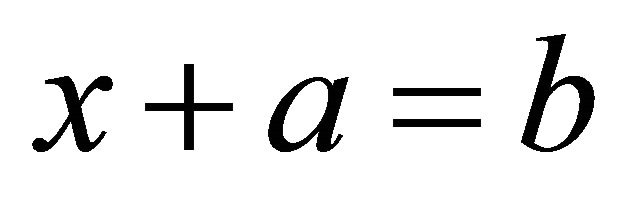 it follows
it follows .
.
By k-closure of a non-empty subset A of a hemiring R we mean the set
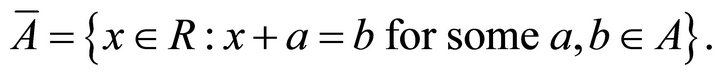
It is clear that if A is a left (right) ideal of R, then A is the smallest left (right) k-ideal of R containing A. So, 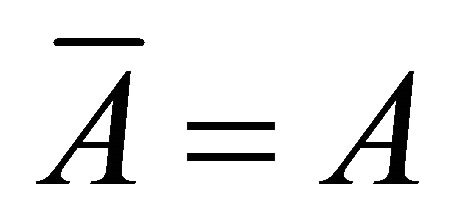 for all left (right) k-ideals of R. Obviously
for all left (right) k-ideals of R. Obviously
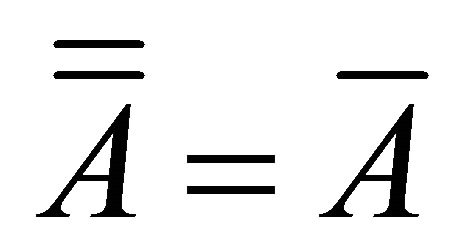 for each non-empty
for each non-empty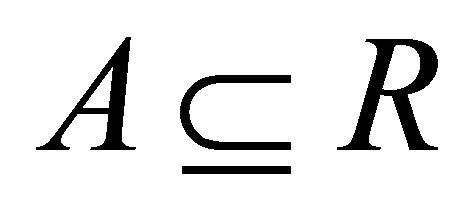 . Also
. Also 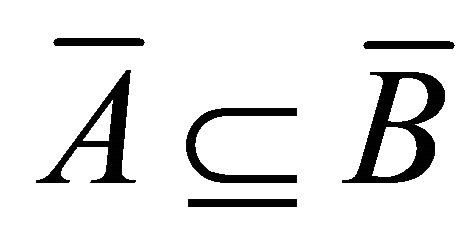 for all
for all .
.
2.1. Lemma
The intersection of any family of left (right) k-ideals of a hemiring R is a left (right) k-ideal of R.
2.2. Lemma
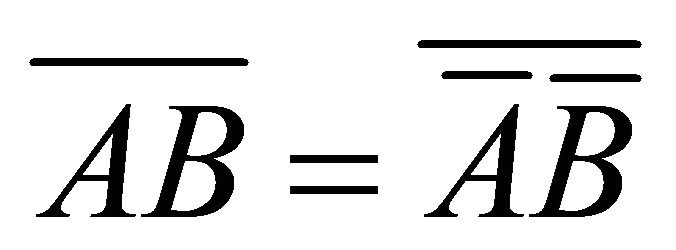 for any subsets A, B of a hemiring R.
for any subsets A, B of a hemiring R.
2.3. Lemma
[30] If A and B are, respectively, right and left k-ideals of a hemiring R, then
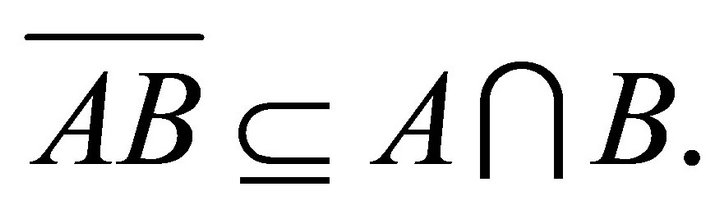
2.4. Definition
[30] A hemiring R is said to be k-hemiregular if for each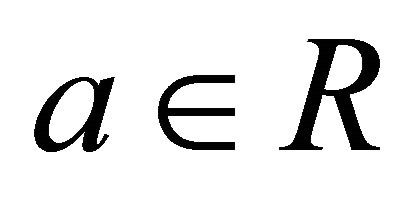 , there exist
, there exist  such that
such that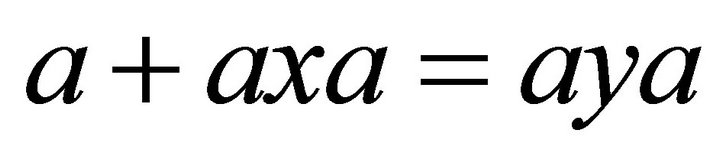 .
.
2.5. Lemma
[30] A hemiring R is k-hemiregular if and only if for any right k-ideal A and any left k-ideal B, we have
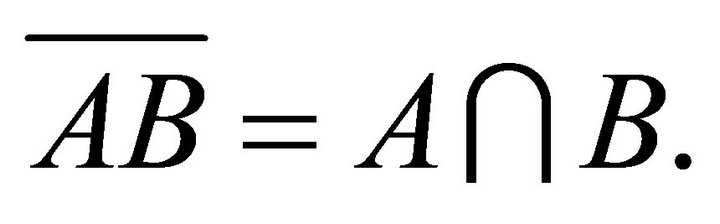
A fuzzy subset 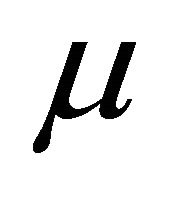 of a non empty set X is a function
of a non empty set X is a function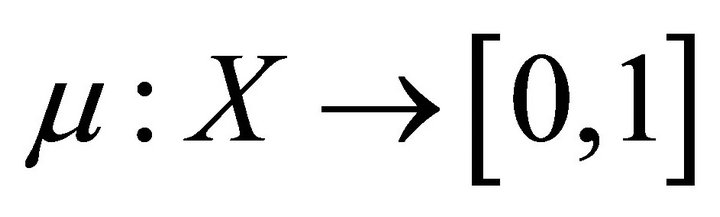 .
. 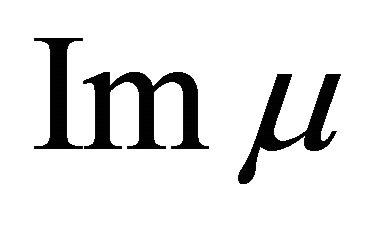 denotes the set of all values of
denotes the set of all values of . A fuzzy subset
. A fuzzy subset  is non-empty if there exist at least one
is non-empty if there exist at least one 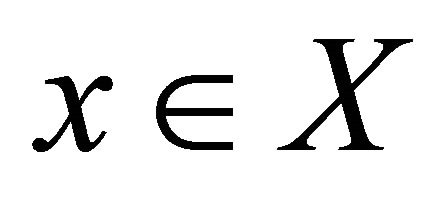 such that
such that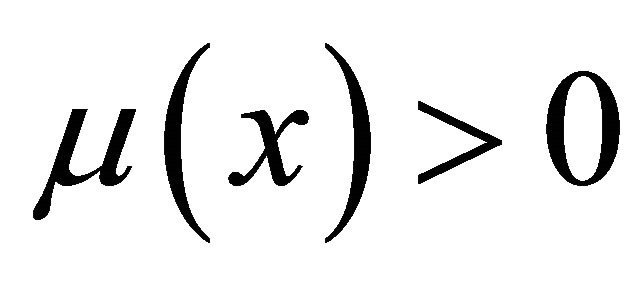 . For any fuzzy subsets
. For any fuzzy subsets ![]() and
and  of X we define
of X we define
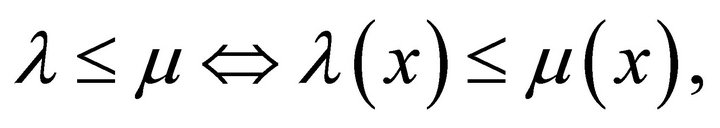
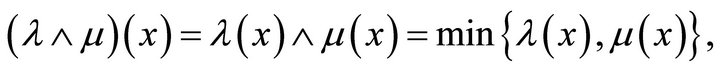

for all .
.
More generally, if  is a collection of fuzzy subsets of
is a collection of fuzzy subsets of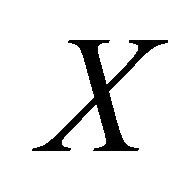 , then by the intersection and the union of this collection we mean the fuzzy subsets
, then by the intersection and the union of this collection we mean the fuzzy subsets

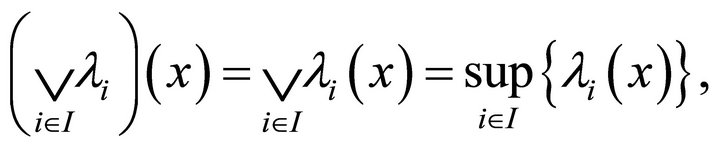
respectively.
A fuzzy subset ![]() of a semiring R is called a fuzzy left (right) ideal of R if for all
of a semiring R is called a fuzzy left (right) ideal of R if for all 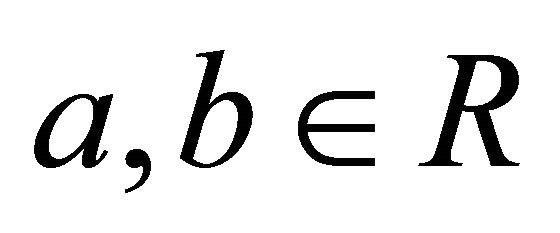 we have 1)
we have 1)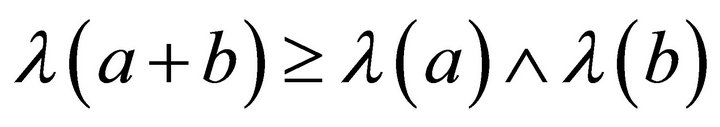 2)
2) .
.
Note that  for all
for all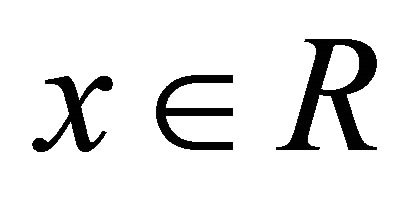 .
.
2.6. Definition
[21] A fuzzy left (right) ideal ![]() of a hemiring R is called a fuzzy left (right) k-ideal if
of a hemiring R is called a fuzzy left (right) k-ideal if
 for all
for all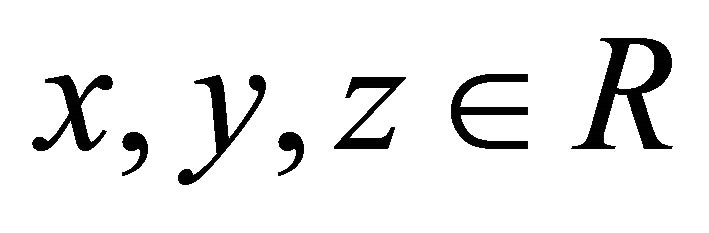 .
.
2.7. Definition
Let ![]() be a fuzzy subset of a universe X and
be a fuzzy subset of a universe X and . Then the subset
. Then the subset  is called the level subset of
is called the level subset of![]() .
.
2.8. Proposition
Let A be a non-empty subset of a hemiring R. Then a fuzzy set  defined by
defined by

where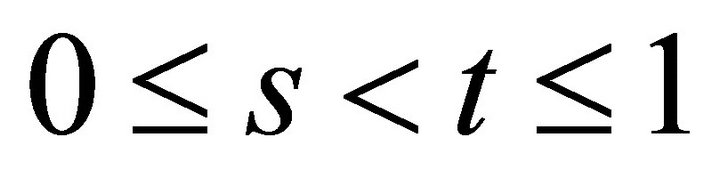 , is a fuzzy left (right) k-ideal of R if and only if A is a left (right) k-ideal of R.
, is a fuzzy left (right) k-ideal of R if and only if A is a left (right) k-ideal of R.
Proof. Straightforward. □
2.9. Proposition
[23] If 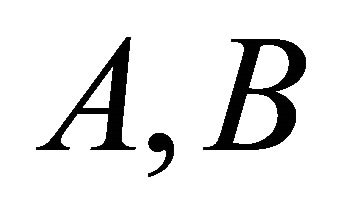 are subsets of a hemiring
are subsets of a hemiring  such that
such that 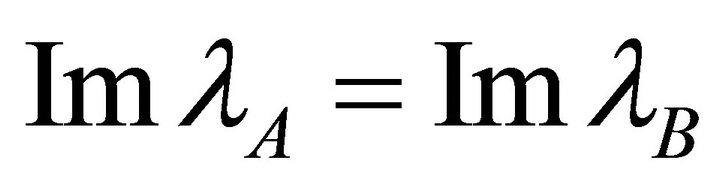 then 1)
then 1) 2)
2)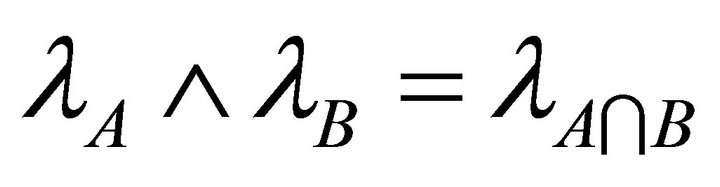 .
.
2.10. Proposition
A fuzzy subset ![]() of a hemiring R is a fuzzy left (right) k-ideal of R if and only if each non-empty level subset of R is a left (right) k-ideal of R.
of a hemiring R is a fuzzy left (right) k-ideal of R if and only if each non-empty level subset of R is a left (right) k-ideal of R.
Proof. Suppose ![]() is a fuzzy left k-ideal of R and
is a fuzzy left k-ideal of R and 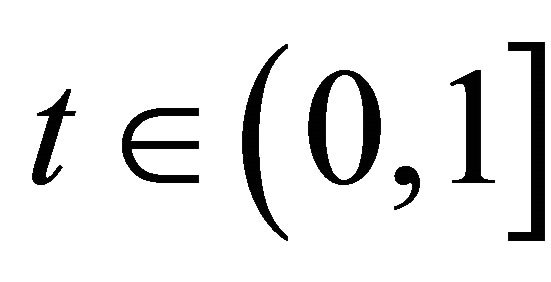 such that
such that . Let
. Let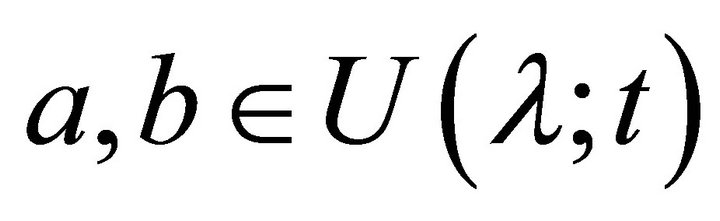 , then
, then  and
and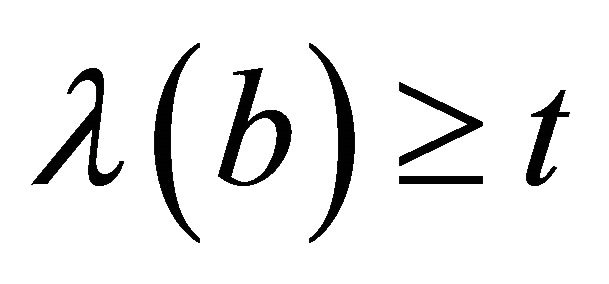 . As
. As , so
, so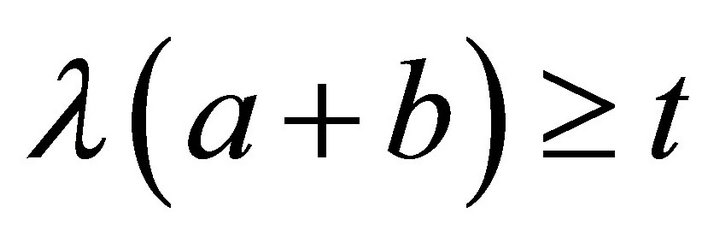 . Hence
. Hence . For
. For ,
,  so
so . This implies
. This implies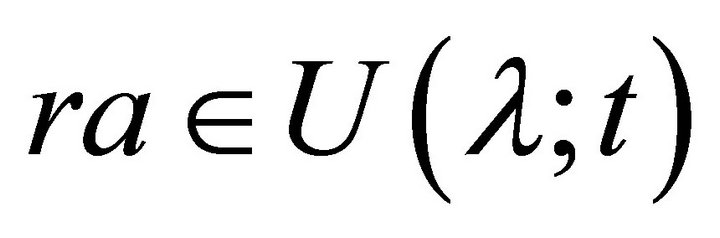 . Hence
. Hence 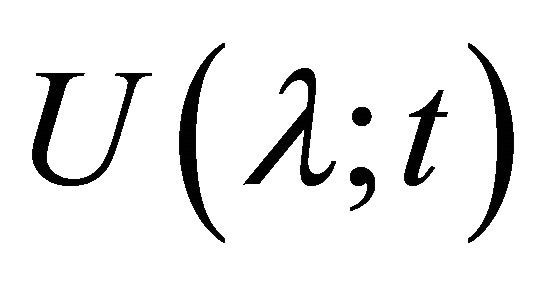 is a left ideal of
is a left ideal of . Now let
. Now let  for some
for some , then
, then 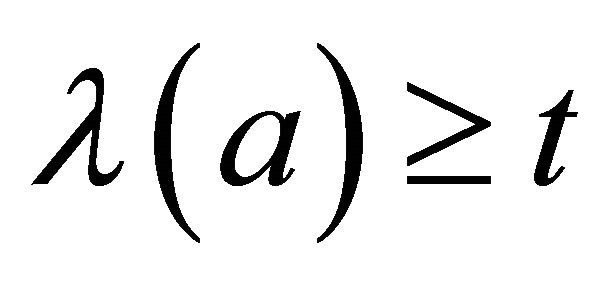 and
and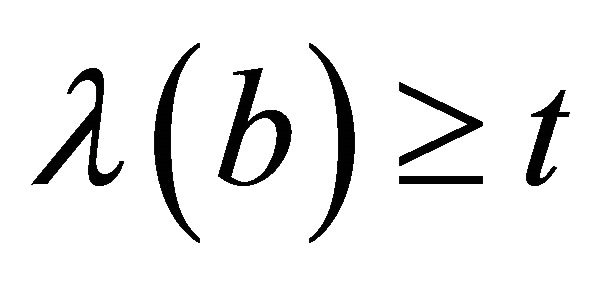 . Since
. Since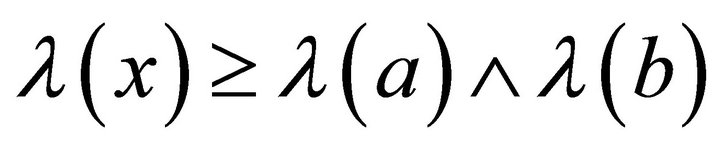 , so
, so . Hence
. Hence  . Thus
. Thus 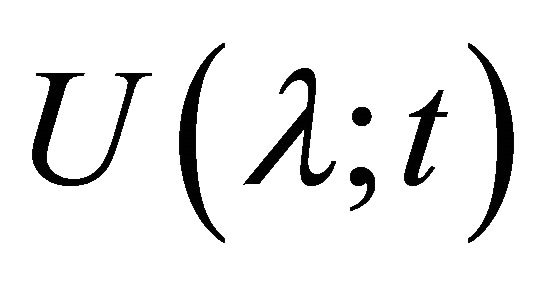 is a left k-ideal of
is a left k-ideal of .
.
Conversely, assume that each non-empty subset  of R is a left k-ideal of R. Let
of R is a left k-ideal of R. Let  such that
such that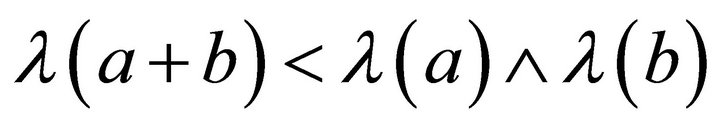 . Take
. Take 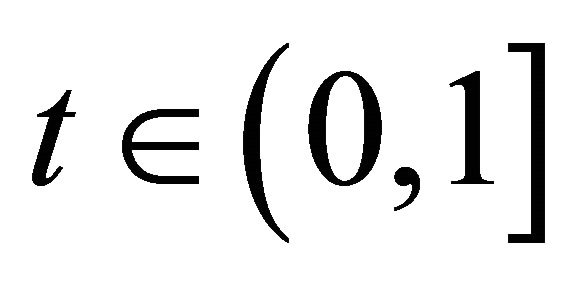 such that
such that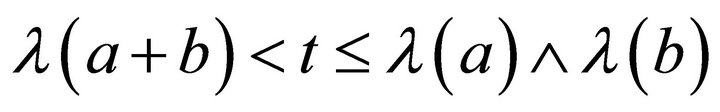 , then
, then 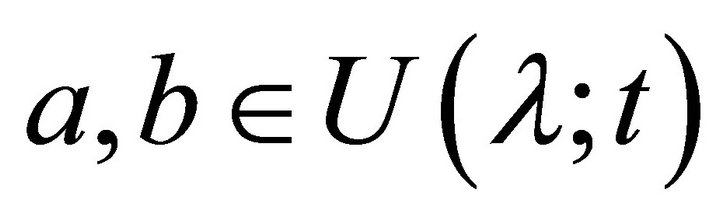 but
but 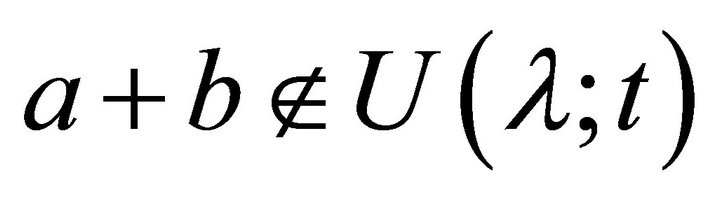 , a contradiction. Hence
, a contradiction. Hence 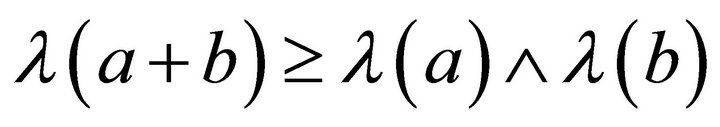 .
.
Similarly we can show that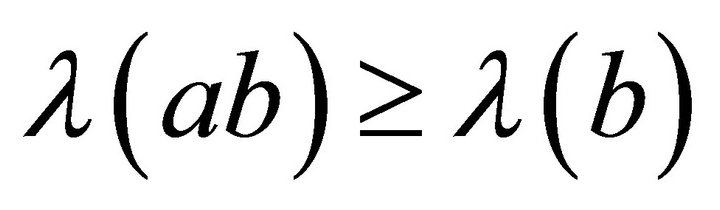 .
.
Let 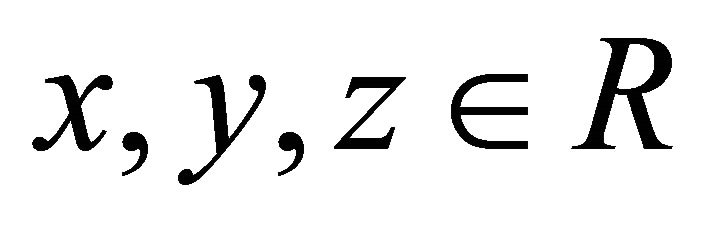 such that
such that . If possible let
. If possible let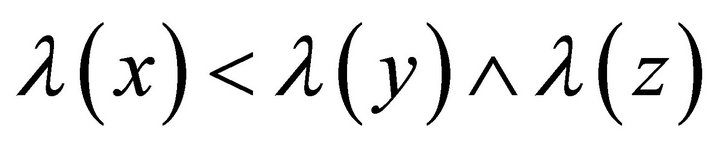 . Take
. Take 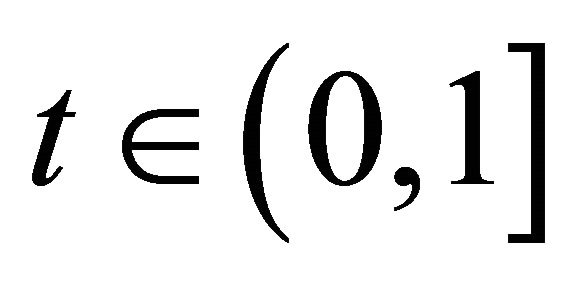 such that
such that 
 , then
, then 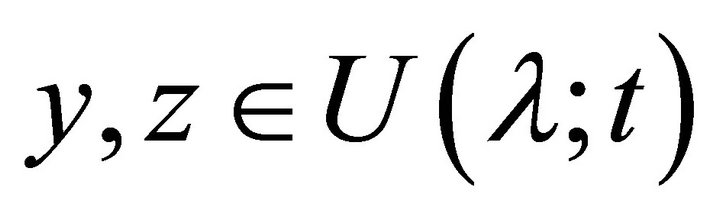 but
but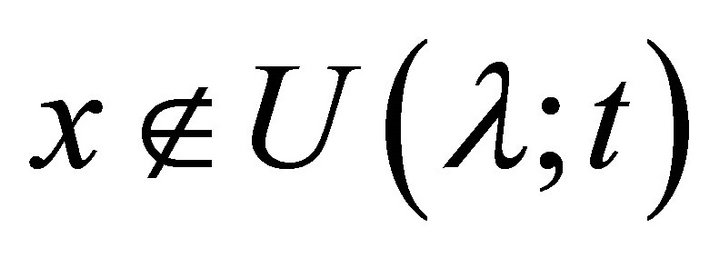 , a contradiction. Hence
, a contradiction. Hence . Thus
. Thus  is a fuzzy left k-ideal of R. □
is a fuzzy left k-ideal of R. □
2.11. Example
The set  with operations addition and multiplication given by the following Cayley tables:
with operations addition and multiplication given by the following Cayley tables:
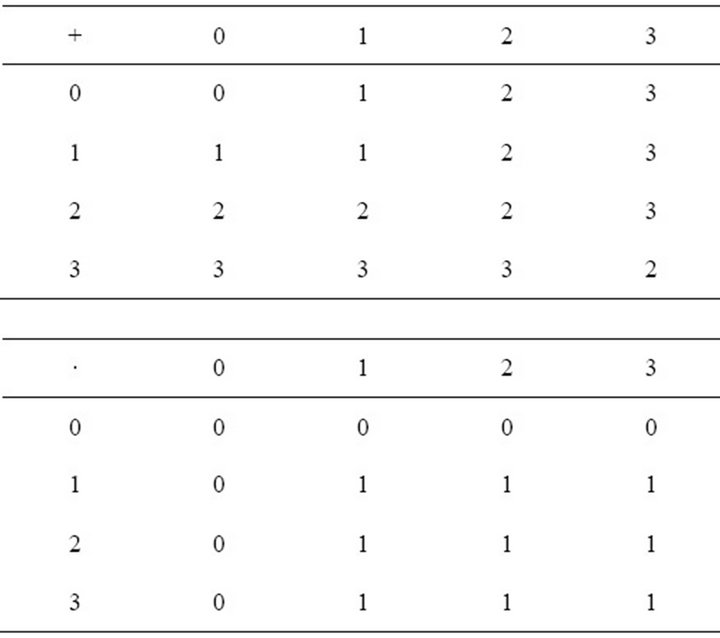
is a hemiring. Ideals in  are
are ,
,  ,
, 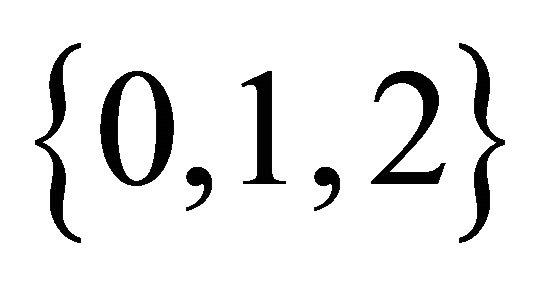 ,
, . All ideals are k-ideals. Let
. All ideals are k-ideals. Let 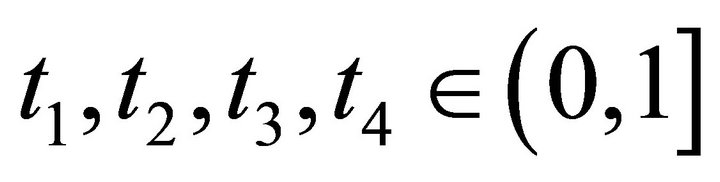 such that
such that .
.
Define  by
by
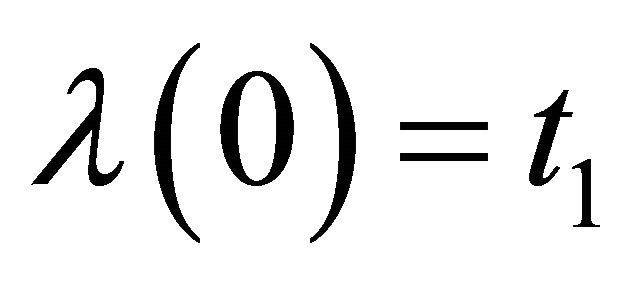
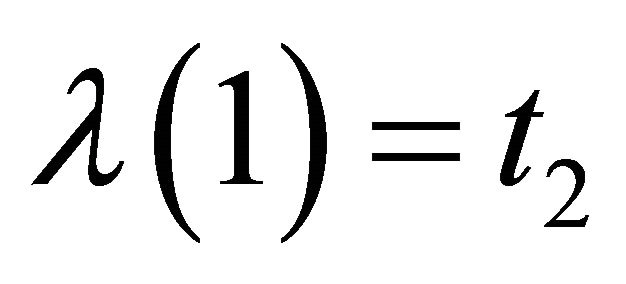


Then

Thus by Proposition 2.10, ![]() is a fuzzy k-ideal of R.
is a fuzzy k-ideal of R.
3. k-Product of Fuzzy Subsets
To avoid repetitions from now R will always mean a hemiring .
.
3.1. Definition
The k-product of two fuzzy subsets 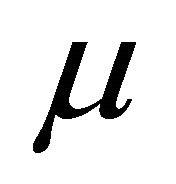 and
and ![]() of R is defined by
of R is defined by

and 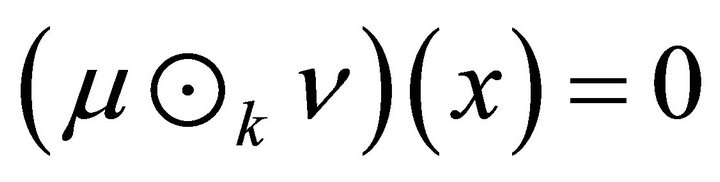 if x can not be expressed as
if x can not be expressed as
 .
.
By direct calculations we obtain the following result.
3.2. Proposition
Let  be fuzzy subsets of R. Then
be fuzzy subsets of R. Then 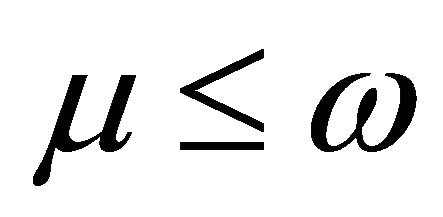 and
and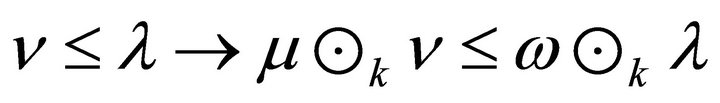 .
.
For any subset A in a hemiring R,  will denote the characteristic function of A.
will denote the characteristic function of A.
3.3. Lemma
Let R be a hemiring and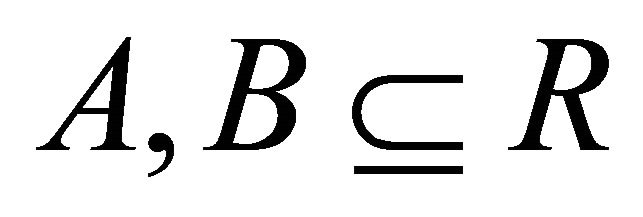 . Then we have 1)
. Then we have 1) 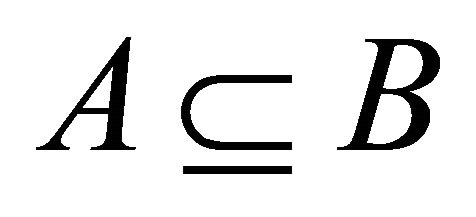 if and only if
if and only if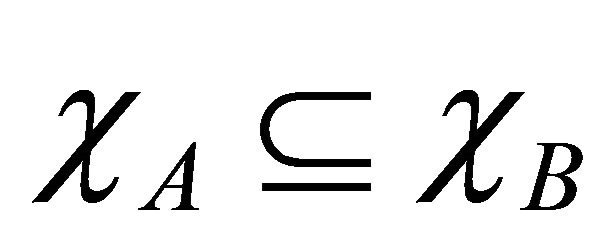 .
.
2)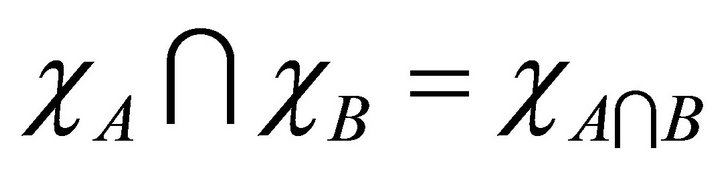 .
.
3) .
.
Proof. 1) and 2) are obvious. For 3) let . If
. If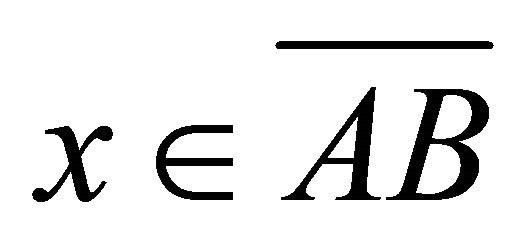 , then
, then 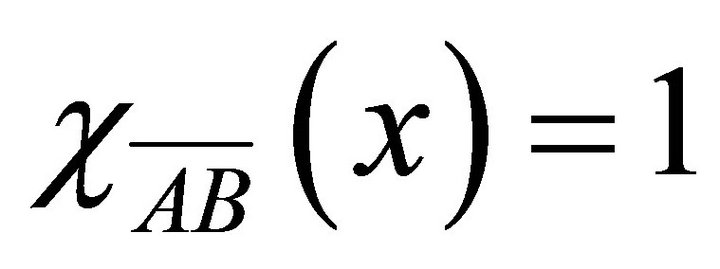 and
and  for some
for some  and
and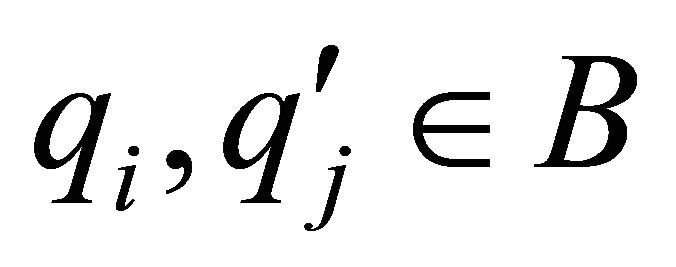 . Thus we have
. Thus we have
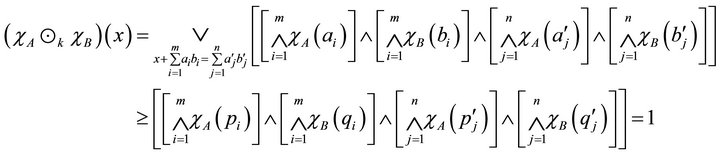
and so
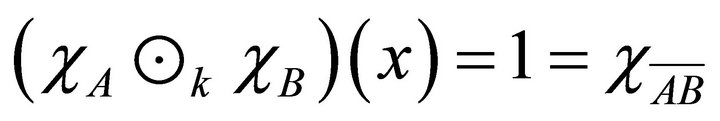
If 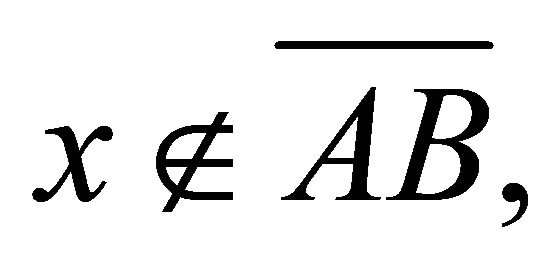 then
then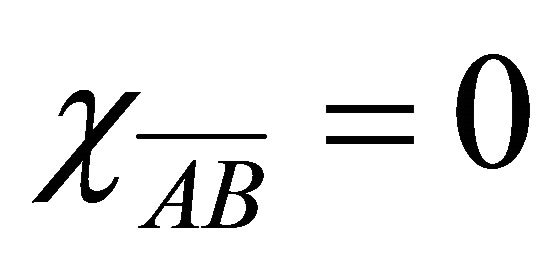 . If possible, let
. If possible, let 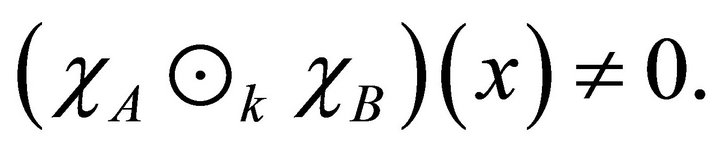 Then
Then

Hence there exist  such that
such that
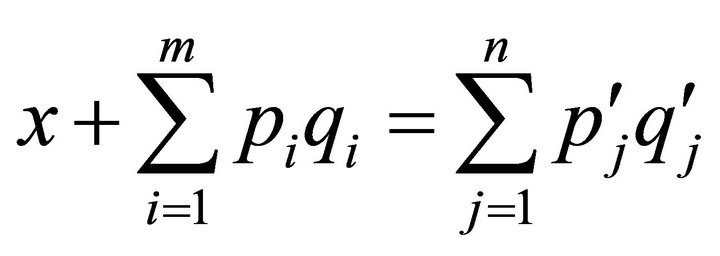
and
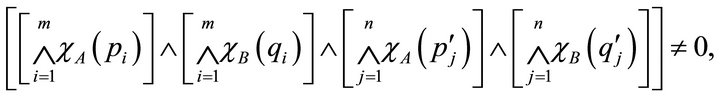
that is

hence 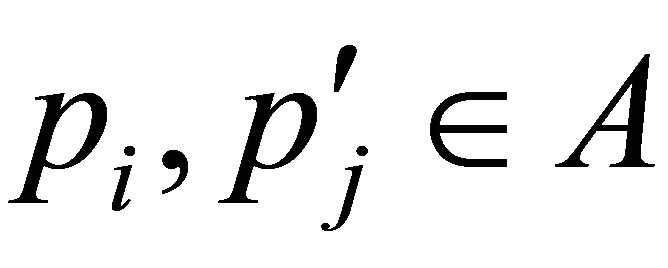 and
and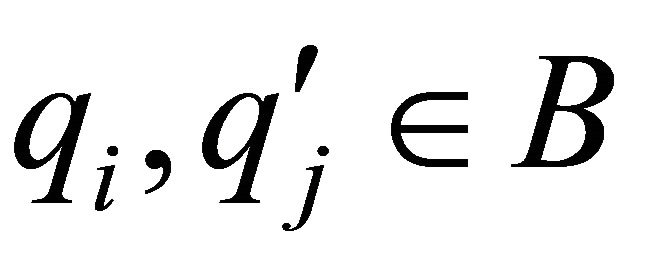 , and so
, and so 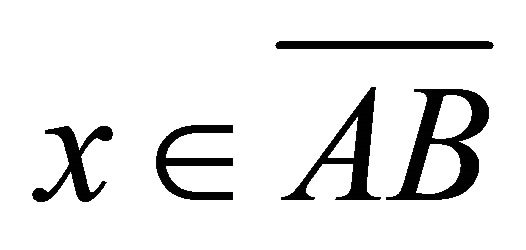 which is a contradiction. Thus we have
which is a contradiction. Thus we have
 .
.
Hence in any case, we have
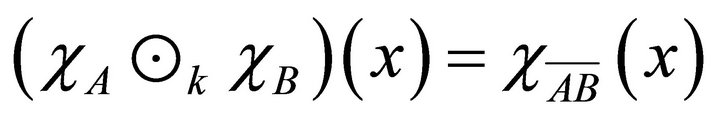 . □
. □
3.4. Theorem
If ![]() are fuzzy
are fuzzy 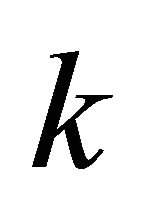 -ideals of
-ideals of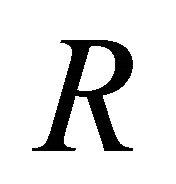 , then
, then  is a fuzzy
is a fuzzy  -ideal of
-ideal of 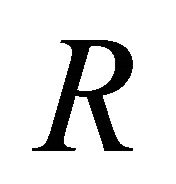 and
and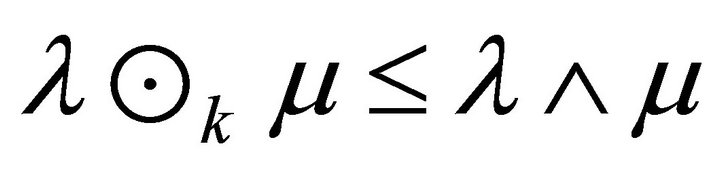 .
.
Proof. Let ![]() be fuzzy
be fuzzy 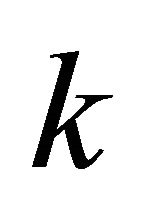 -ideals of
-ideals of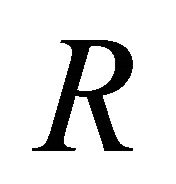 . Let
. Let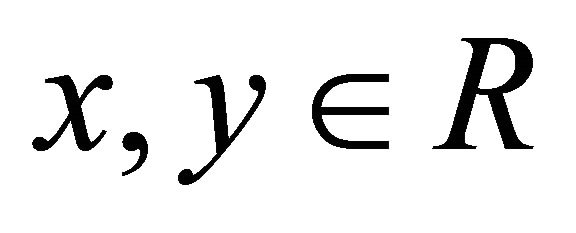 , then
, then

and

Thus

Since for each expression 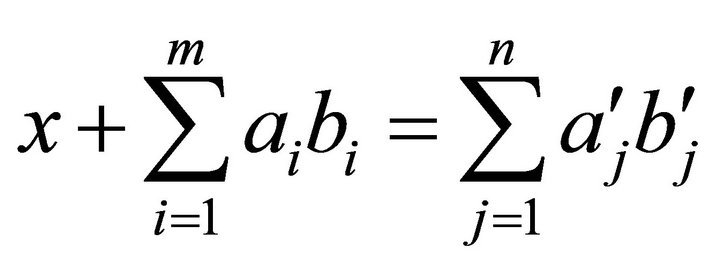 and
and  we have
we have
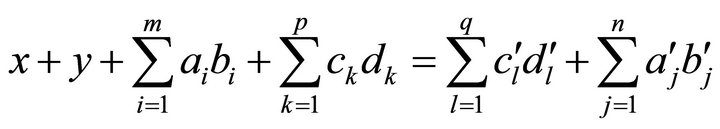 so we have
so we have
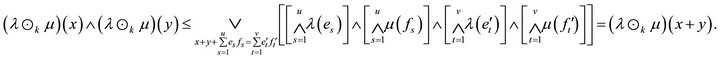
Similarly,

Analogously we can verify that
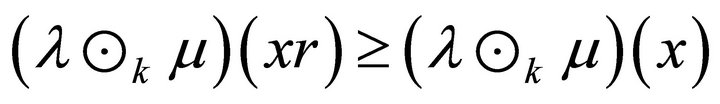 for all
for all . This means that
. This means that  is a fuzzy ideal of
is a fuzzy ideal of .
.
To prove that  implies
implies

observe that
 (1)
(1)
together with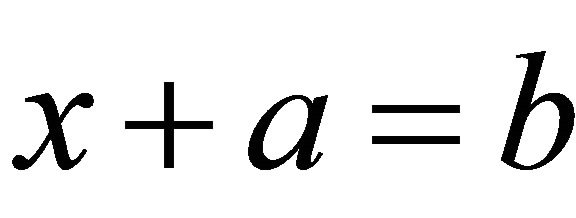 , gives
, gives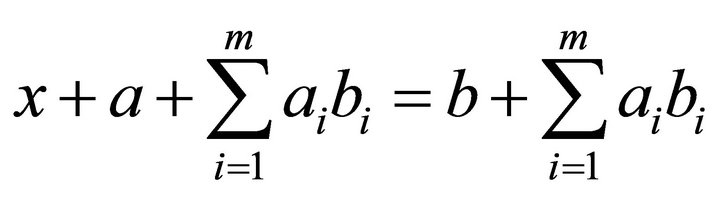 . Thus
. Thus
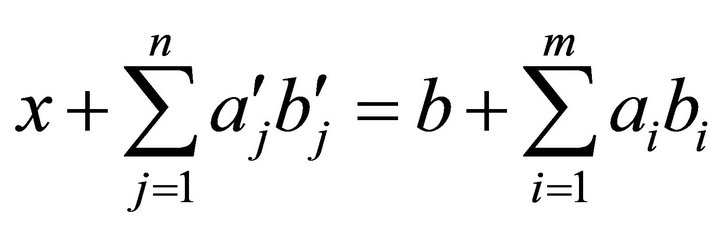
and, consequently,

Therefore
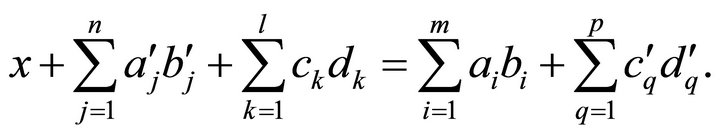 (2)
(2)
Now, we have

Thus
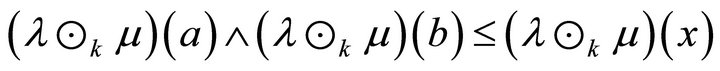 .
.
Hence 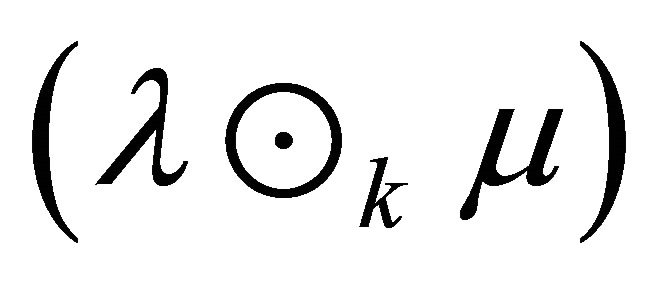 is a fuzzy k-ideal of R.
is a fuzzy k-ideal of R.
By simple calculations we can prove that
 . □
. □
3.5. Definition
The k-sum 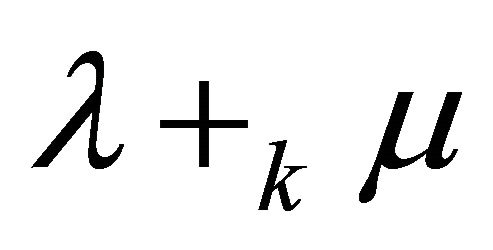 of fuzzy subsets
of fuzzy subsets ![]() and
and  of R is defined by
of R is defined by

where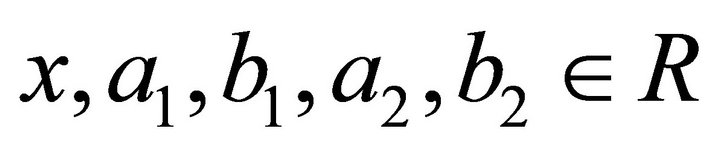 .
.
3.6. Theorem
The k-sum of fuzzy k-ideals of R is also a fuzzy k-ideal of R.
Proof. Let ![]() be fuzzy k-ideals of R. Then for
be fuzzy k-ideals of R. Then for 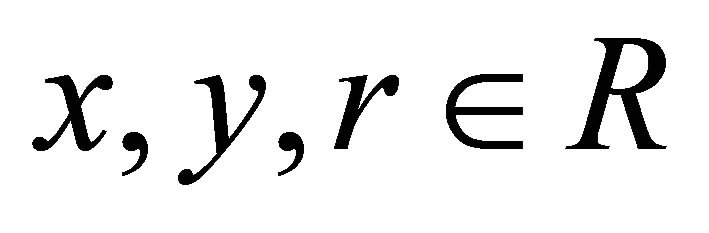 we have
we have
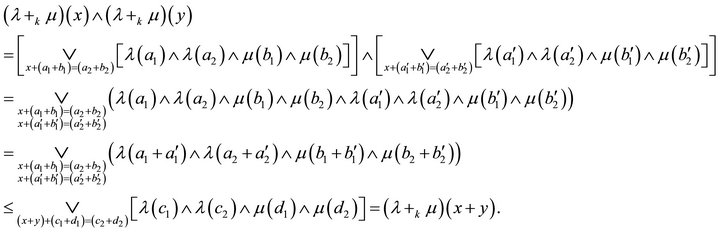
Similarly,
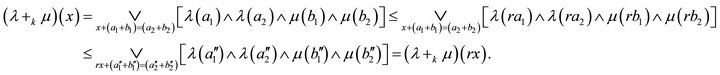
Similarly  This proves that
This proves that 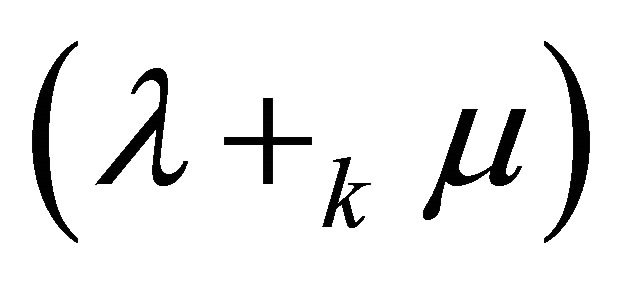 is a fuzzy ideal of
is a fuzzy ideal of .
.
Now we show that  implies
implies
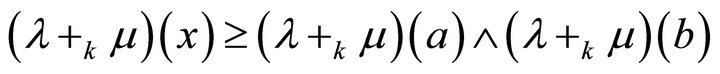 . For this let
. For this let 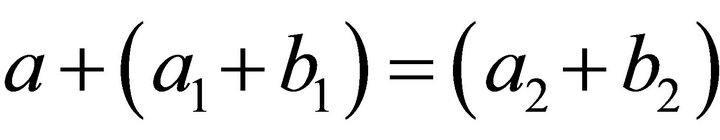 and
and 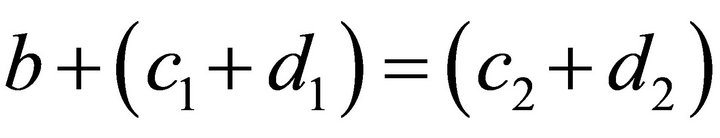 Then,
Then,
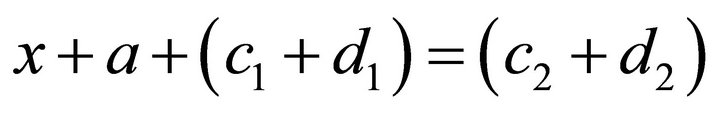
whence

and
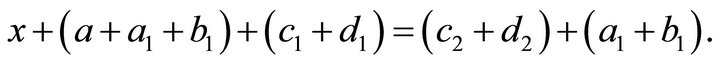
Then
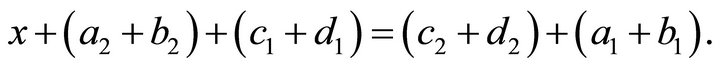
Thus
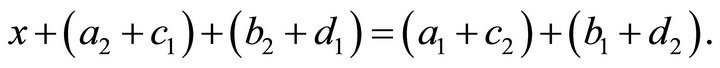
Therefore
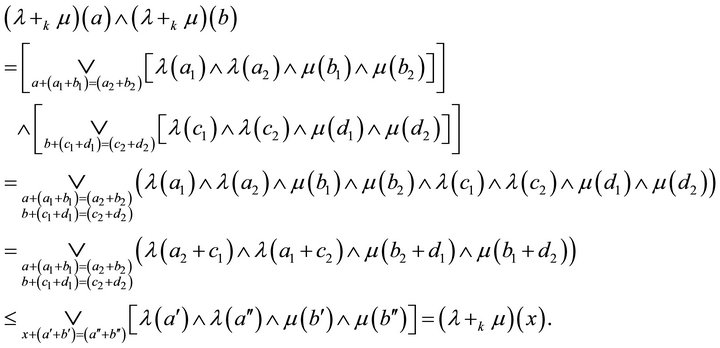
Thus 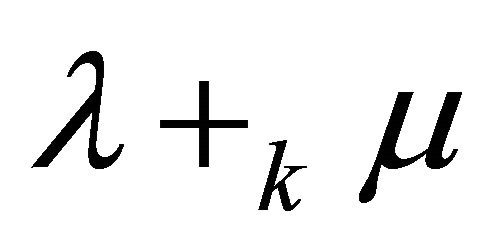 is a fuzzy k-ideal of
is a fuzzy k-ideal of . □
. □
3.7. Theorem
If  is a fuzzy subset of a hemiring R, then the following are equivalent:
is a fuzzy subset of a hemiring R, then the following are equivalent:
1)  satisfies a)
satisfies a)  and b)
and b)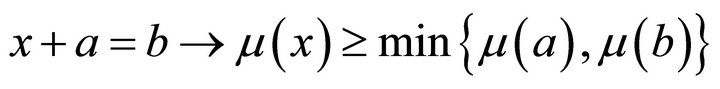 2)
2)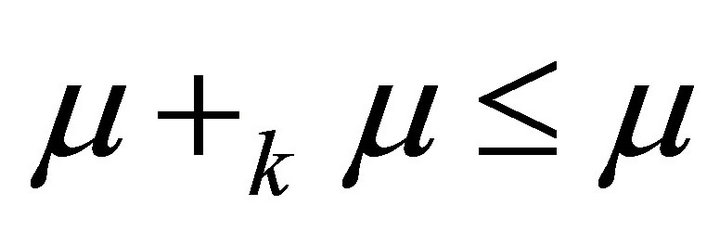 .
.
Proof. 1) ® 2) Let , then
, then

Thus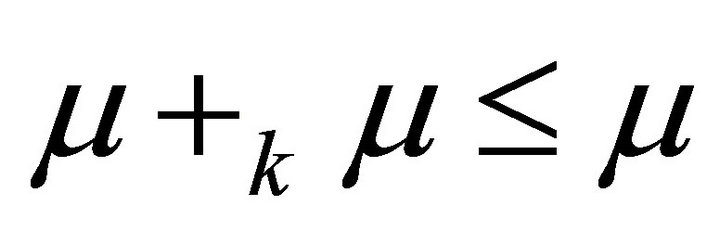 .
.
2) ® 1) First we show that  for all
for all .
.
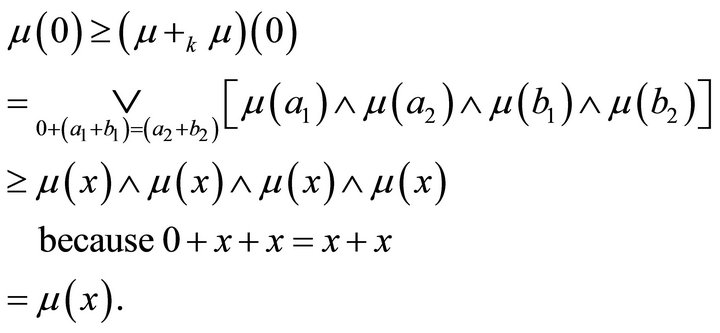
Thus  for all
for all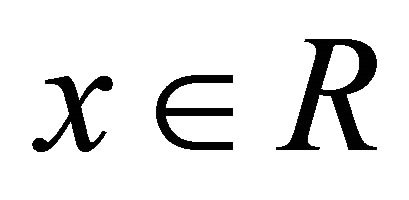 .
.
Now
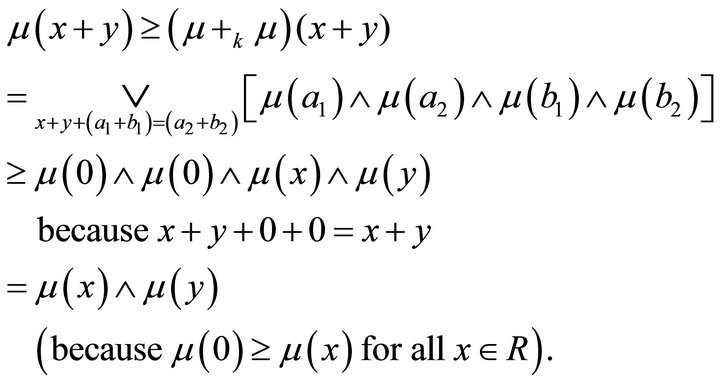
Again
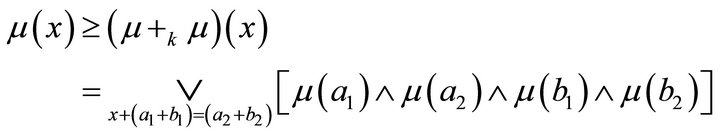
If  then
then 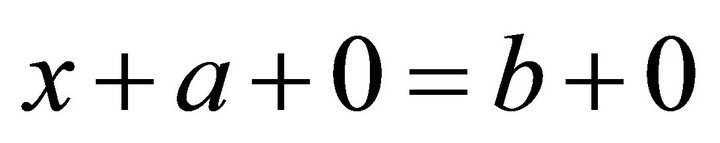 and so
and so
 □
□
3.8. Lemma
A fuzzy subset  in a hemiring R is a fuzzy left (right) k-ideal if and only if 1)
in a hemiring R is a fuzzy left (right) k-ideal if and only if 1) 2)
2)
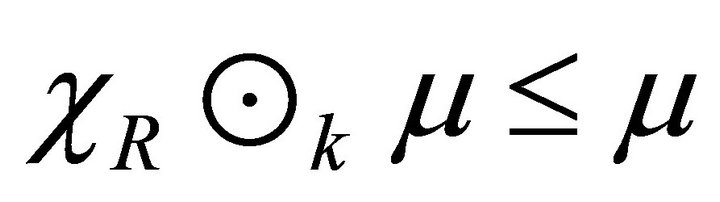 .
.
Proof. Let 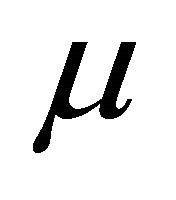 be a fuzzy left k-ideal of R. By Theorem 3.7,
be a fuzzy left k-ideal of R. By Theorem 3.7, 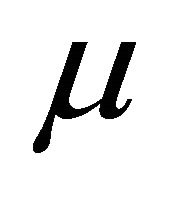 satisfies 1). Now we prove condition 2). Let
satisfies 1). Now we prove condition 2). Let . If
. If , then
, then
 . Otherwise, there exist elements
. Otherwise, there exist elements
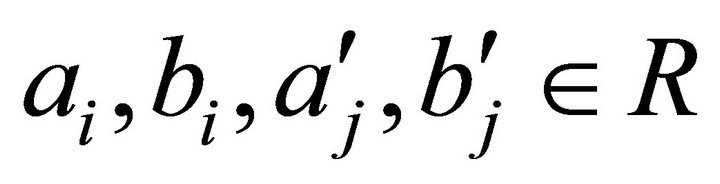 such that
such that . Then we have
. Then we have
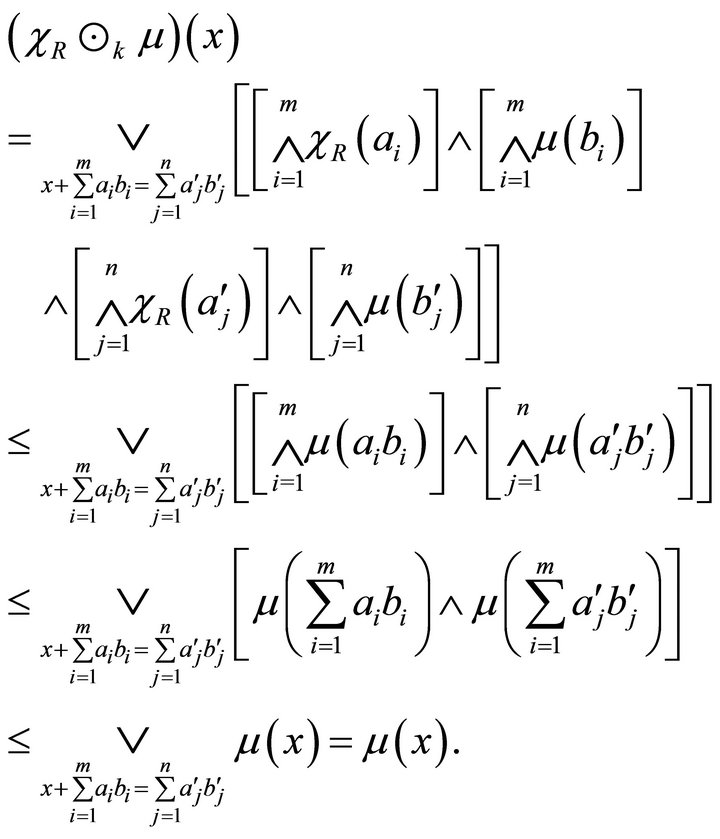
This implies that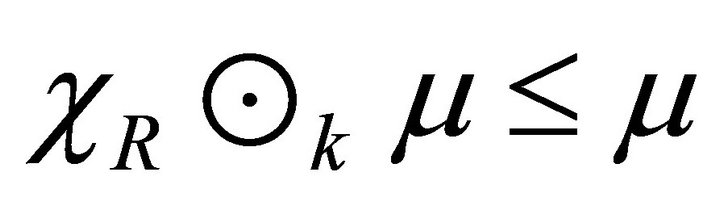 .
.
Conversely, assume that the given conditions hold. In order to show that  is a fuzzy left k-ideal of R it is sufficient to show that the condition
is a fuzzy left k-ideal of R it is sufficient to show that the condition 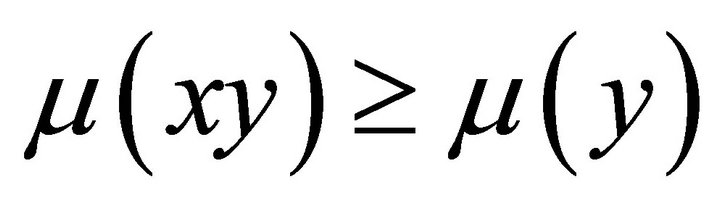 holds. Let
holds. Let . Then we have
. Then we have
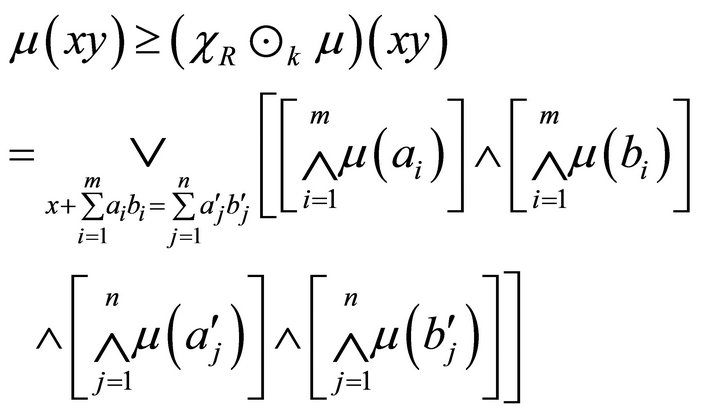
since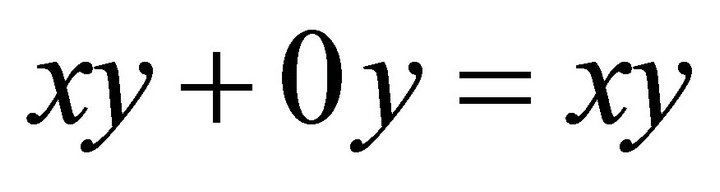 , so
, so 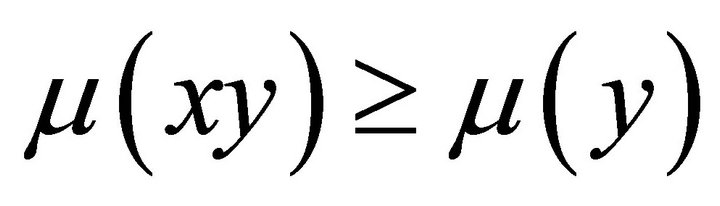 and
and 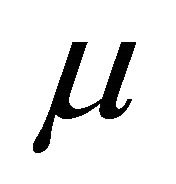 is a fuzzy left k-ideal of R. □
is a fuzzy left k-ideal of R. □
For k-hemiregular hemirings we have stronger result.
3.9. Theorem
A hemiring R is k-hemiregular if and only if for any fuzzy right k-ideal  and any fuzzy left k-ideal
and any fuzzy left k-ideal ![]() of R we have
of R we have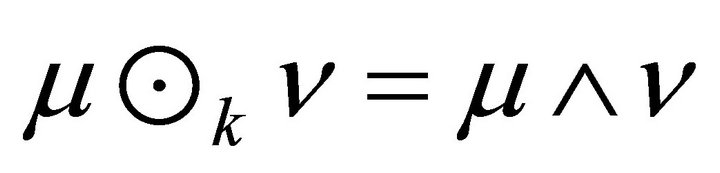 .
.
Proof. Let R be a k-hemiregular hemiring and 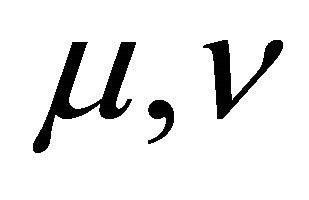 be fuzzy right k-ideal and fuzzy left k-ideal of R, respectively. Then by Lemma 3.8, we have
be fuzzy right k-ideal and fuzzy left k-ideal of R, respectively. Then by Lemma 3.8, we have 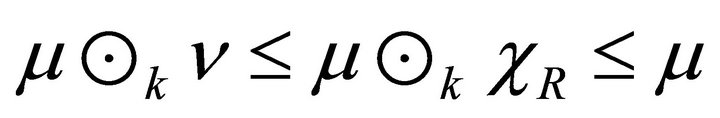 and
and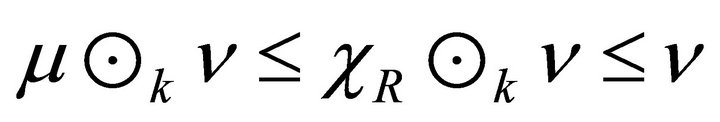 . Thus
. Thus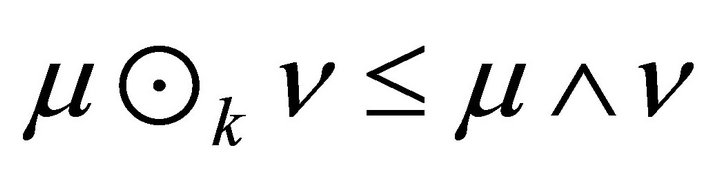 . To show the converse inclusion, let
. To show the converse inclusion, let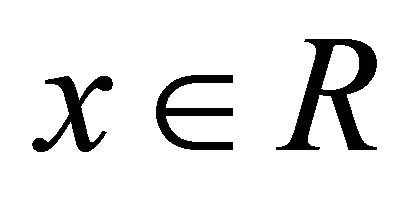 . Since R is k-hemiregular, so there exist
. Since R is k-hemiregular, so there exist  such that
such that . Then we have
. Then we have
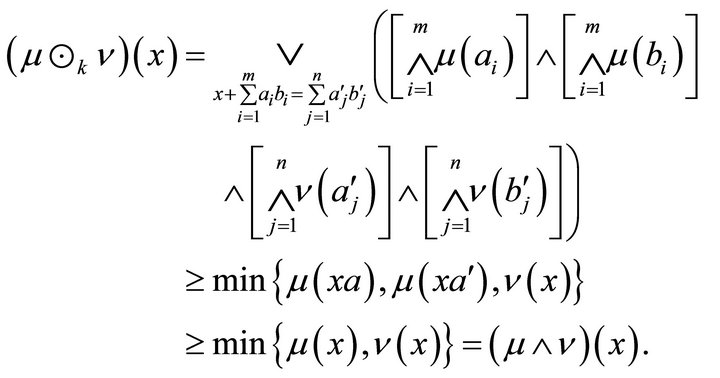
This implies that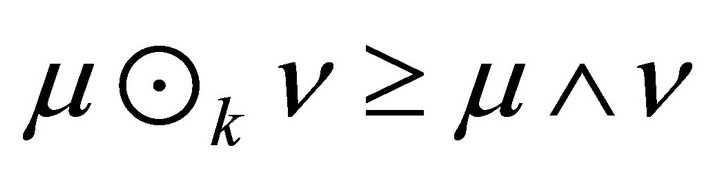 . Therefore
. Therefore  .
.
Conversely, let C, D be any right k-ideal and any left k-ideal of R, respectively. Then the characteristic functions ,
, 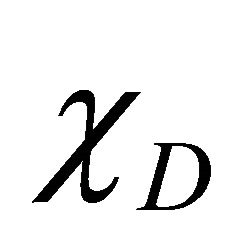 of C, D are fuzzy right k-ideal and fuzzy left k-ideal of R, respectively. Now, by the assumption and Lemma 3.3, we have
of C, D are fuzzy right k-ideal and fuzzy left k-ideal of R, respectively. Now, by the assumption and Lemma 3.3, we have
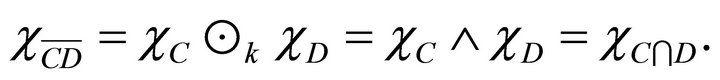
So,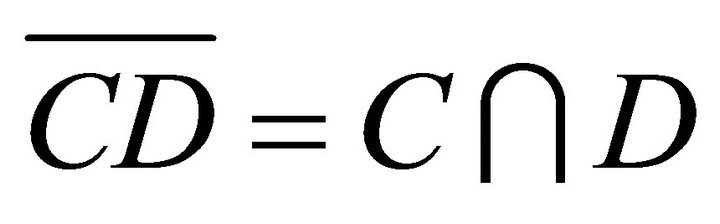 . Hence by Lemma 2.5, R is khemiregular hemiring. □
. Hence by Lemma 2.5, R is khemiregular hemiring. □
4. Idempotent k-Ideals
From Lemma 2.5 it follows that in a k-hemiregular hemiring every k-ideal A is k-idempotent, that is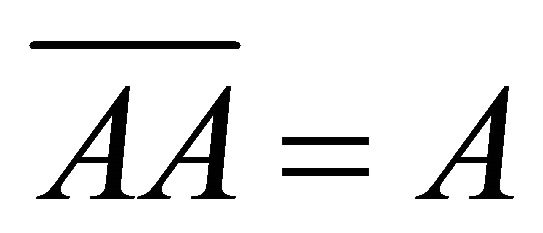 . On the other hand, in such hemirings we have
. On the other hand, in such hemirings we have  for all fuzzy k-ideals
for all fuzzy k-ideals![]() . Fuzzy k-ideal with this property will be called idempotent.
. Fuzzy k-ideal with this property will be called idempotent.
4.1. Proposition
The following statements are equivalent for a hemiring R:
1) Each k-ideal of R is idempotent.
2) 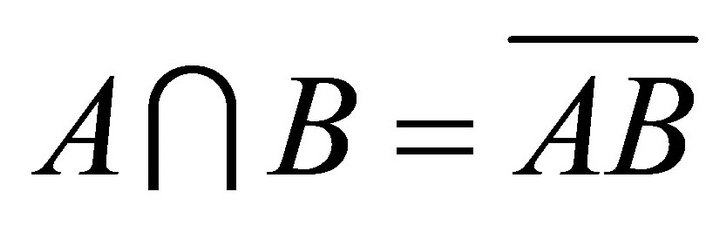 for each pair of k-ideals A, B of R.
for each pair of k-ideals A, B of R.
3)  for every
for every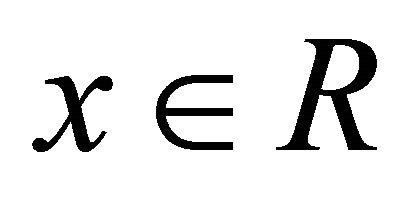 .
.
4)  for every non empty subset X of R.
for every non empty subset X of R.
5)  for every k-ideal A of R.
for every k-ideal A of R.
If R is commutative, then the above assertions are equivalent to 6) R is k-hemiregular.
Proof. 1) ® 2) Assume that each k-ideal of R is idempotent and A, B are k-ideals of R. By Lemma 2.3,
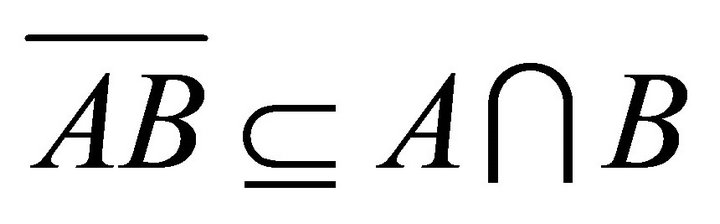 . Since
. Since 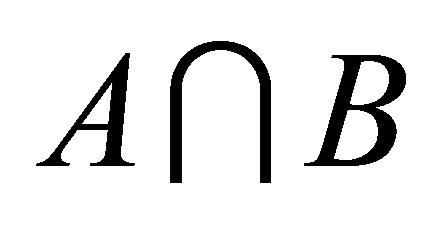 is a k-ideal of R, so by 1)
is a k-ideal of R, so by 1)
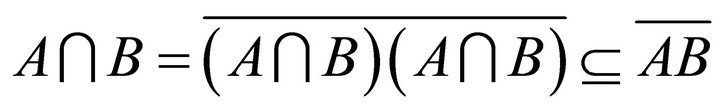 . Thus
. Thus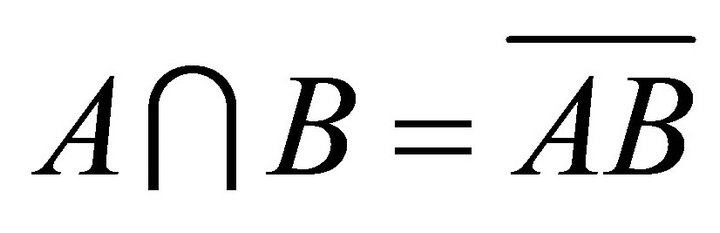 .
.
2) ® 1) Obvious.
1) ® 3) Let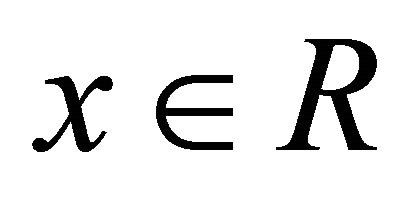 . The smallest k-ideal containing x has the form
. The smallest k-ideal containing x has the form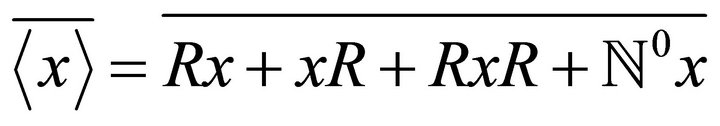 , where
, where 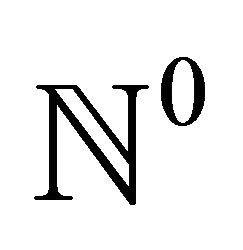 is the set of whole numbers. By hypothesis
is the set of whole numbers. By hypothesis
 . Thus
. Thus

3) ® 4) This is obvious.
4) ® 5) Let A be a k-ideal of R. Then
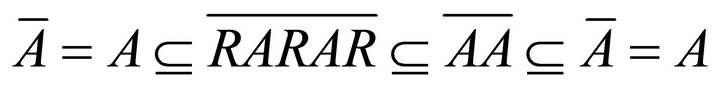 . Hence
. Hence .
.
5) ® 1) This is obvious.
If R is commutative then by Lemma 2.5, . □
. □
4.2. Proposition
The following statements are equivalent for a hemiring R.
1) Each fuzzy k-ideal of R is idempotent.
2) 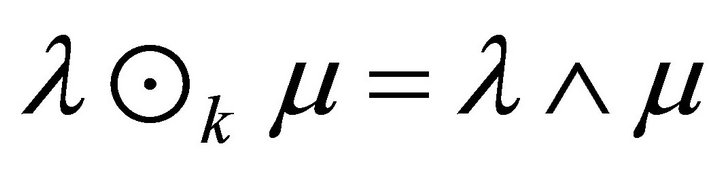 for all fuzzy k-ideals of R.
for all fuzzy k-ideals of R.
If R is commutative, then the above assertions are equivalent to 3) R is k-hemiregular.
Proof. 1) ® 2) Let ![]() and
and 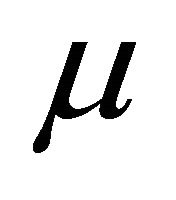 be fuzzy k-ideals of R. By Proposition 3.2,
be fuzzy k-ideals of R. By Proposition 3.2, . Since
. Since  is a fuzzy k-ideal of R, so by hypothesis
is a fuzzy k-ideal of R, so by hypothesis 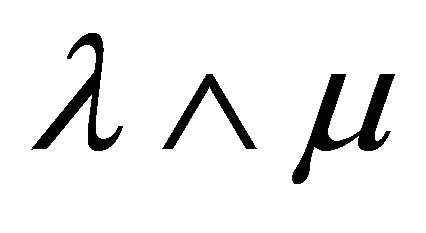 is idempotent. Thus
is idempotent. Thus . By Theorem 3.4,
. By Theorem 3.4,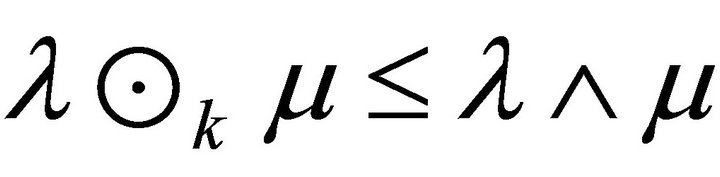 . Thus
. Thus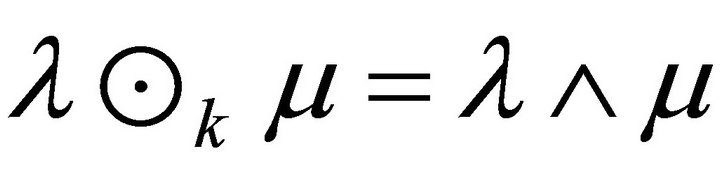 .
.
2) ® 1) Obvious.
If R is commutative then by Theorem 3.9, . □
. □
4.3. Theorem
Let R be a hemiring with identity 1, then the following assertions are equivalent:
1) Each k-ideal of R is idempotent.
2) 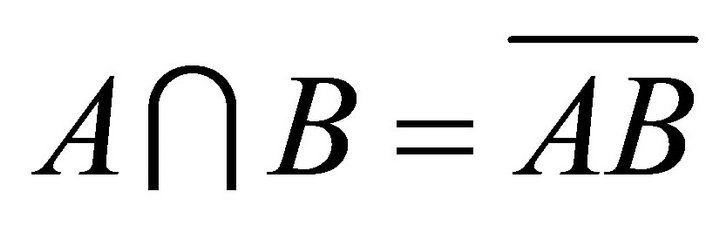 for each pair of k-ideals A, B of R.
for each pair of k-ideals A, B of R.
3) Each fuzzy k-ideal of R is idempotent.
4) 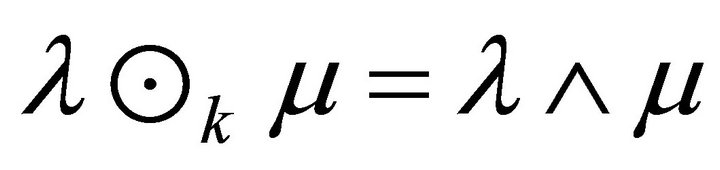 for all fuzzy k-ideals of R.
for all fuzzy k-ideals of R.
Proof.  By Proposition 4.1.
By Proposition 4.1.
 By Proposition 4.2.
By Proposition 4.2.
1) ® 3) Let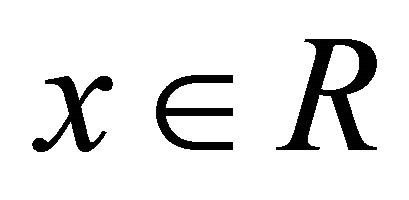 . The smallest k-ideal of R containing x has the form
. The smallest k-ideal of R containing x has the form . By hypothesis, we have
. By hypothesis, we have
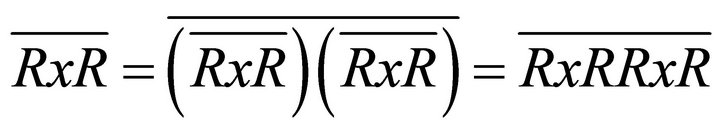 . Thus
. Thus
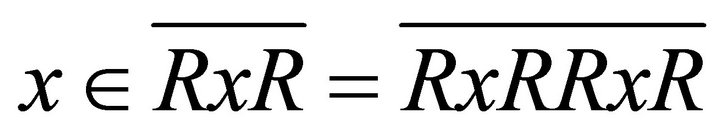 , this implies
, this implies

for some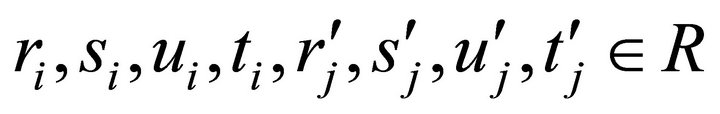 .
.
As 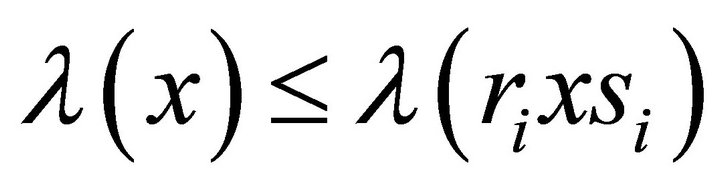 and
and 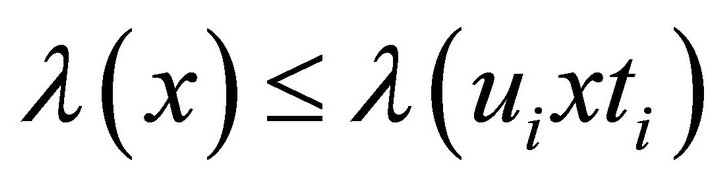 for each
for each , so
, so
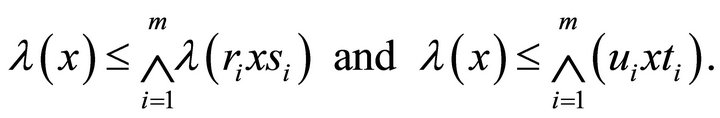
Therefore .
.
Similarly
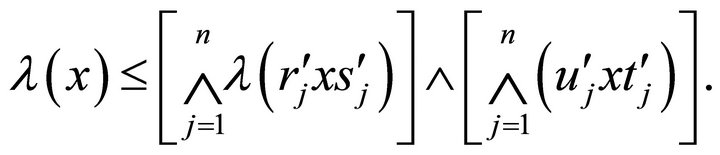
Therefore
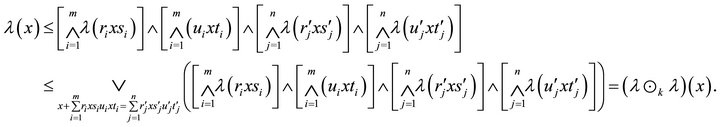
Hence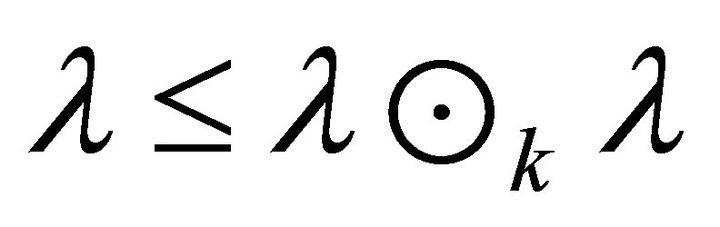 . By Theorem 3.4,
. By Theorem 3.4,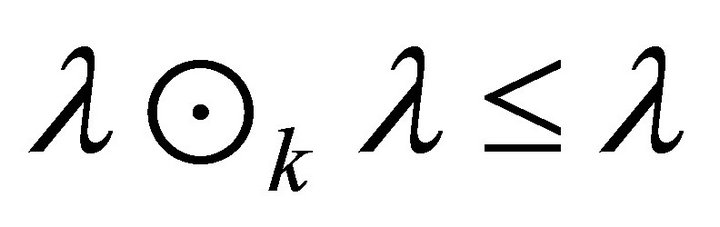 . Thus
. Thus .
.
3) ® 1) Let A be a k-ideal of R, then the characteristic function 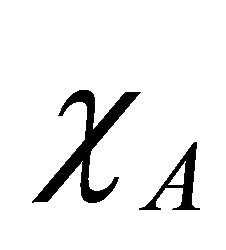 of A is a fuzzy k-ideal of R. Hence by hypothesis
of A is a fuzzy k-ideal of R. Hence by hypothesis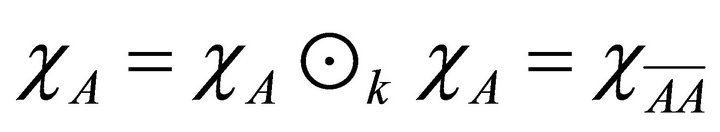 . Thus
. Thus . □
. □
4.4. Theorem
If each k-ideal of R is idempotent, then the collection of all k-ideals of R is a complete Brouwerian lattice.
Proof. Let 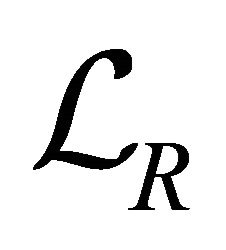 be the collection of all k-ideals of R, then
be the collection of all k-ideals of R, then  is a poset under the inclusion of sets. It is not difficult to see that
is a poset under the inclusion of sets. It is not difficult to see that 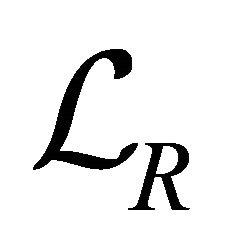 is a complete lattice under the operations
is a complete lattice under the operations![]() ,
, ![]() defined as
defined as  and
and  .
.
We now show that 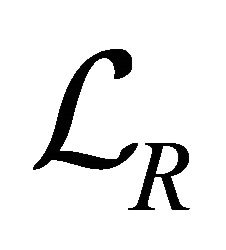 is a Brouwerian lattice, that is, for any
is a Brouwerian lattice, that is, for any 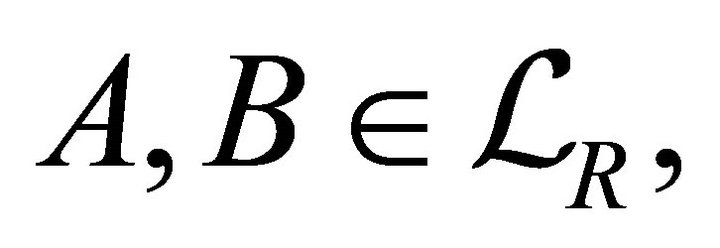 the set
the set 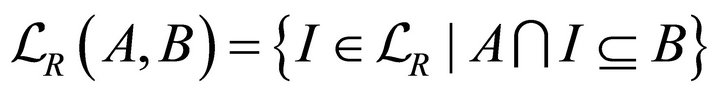 contains a greatest element.
contains a greatest element.
By Zorn’s Lemma the set 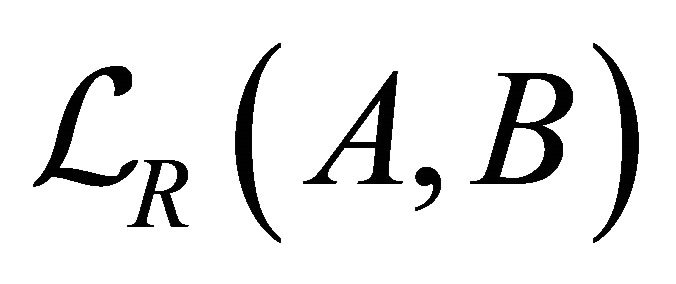 contains a maximal element M. Since each k-ideal of R is idempotent, so
contains a maximal element M. Since each k-ideal of R is idempotent, so 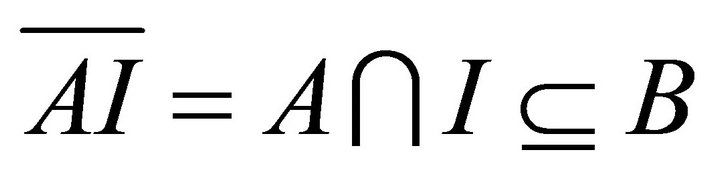 and
and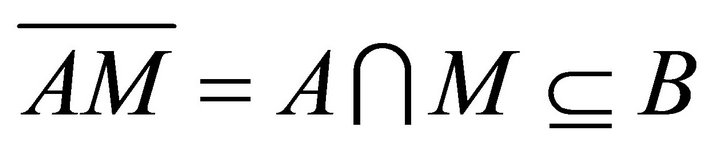 . Thus
. Thus
 . Consequently,
. Consequently, .
.
Since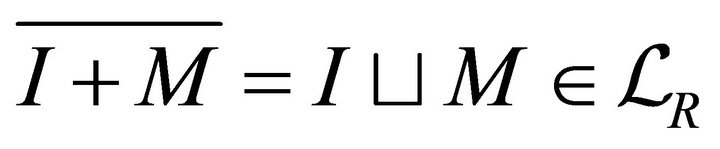 , for every
, for every 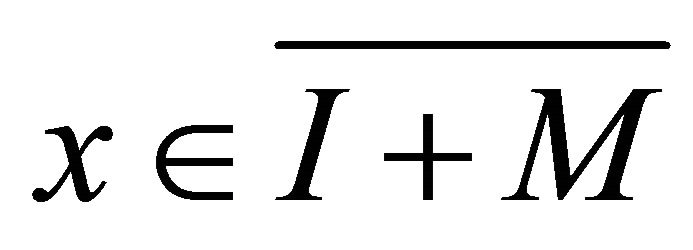 there exist
there exist 
 such that
such that
 . Thus
. Thus 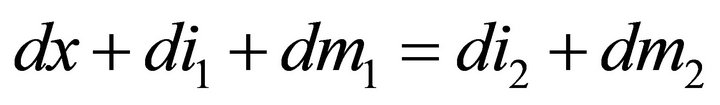 for any
for any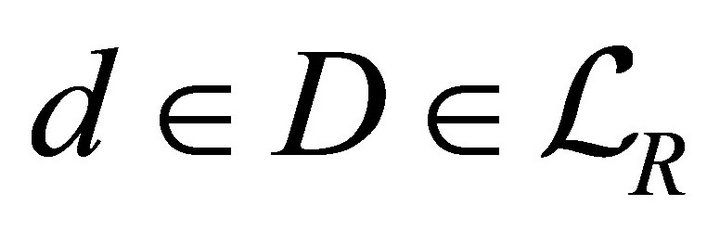 . As
. As 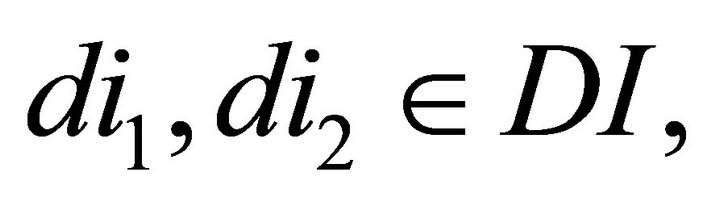
 we have
we have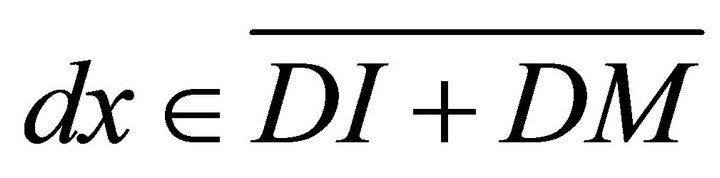 , which implies
, which implies
 .
.
Hence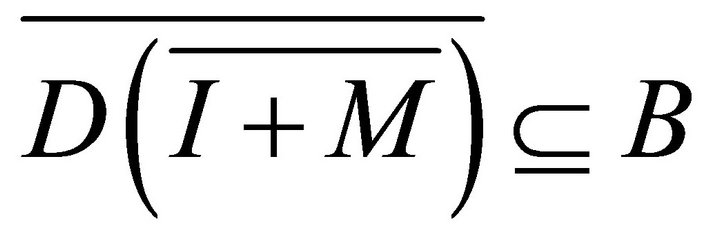 . This means that
. This means that
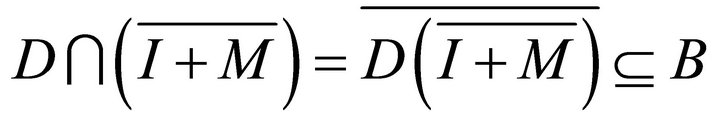 , i.e.,
, i.e.,  whence
whence 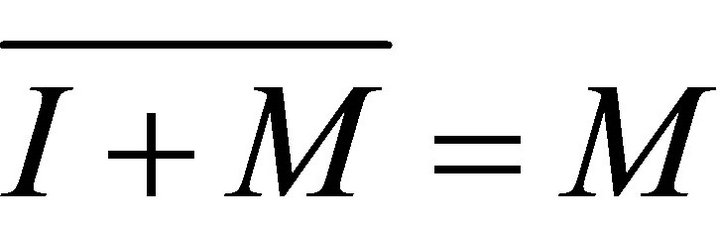 because M is maximal in
because M is maximal in . Therefore
. Therefore  for every
for every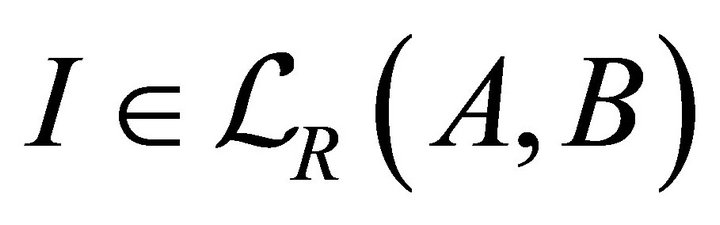 .
.
□
4.5. Corollary
If each k-ideal of R is idempotent, then the lattice  of all k-ideal of R is distributive.
of all k-ideal of R is distributive.
Proof. Each complete Brouwerian lattice is distributive (cf. [31], 11.11). □
4.6. Theorem
Each fuzzy k-ideal of R is idempotent if and only if the set of all fuzzy k-ideal of R (ordered by ≤) forms a distributive lattice under the k-sum and k-product of fuzzy k-ideals with .
.
Proof. Suppose that each fuzzy k-ideal of R is idempotent. Then by Proposition 4.2,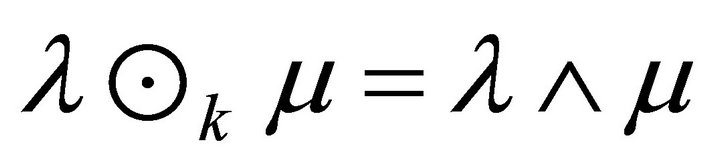 . Let
. Let 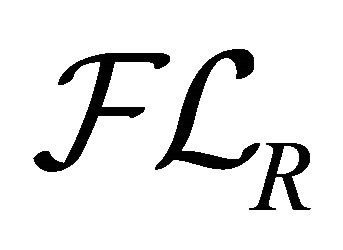 be the collection of all fuzzy k-ideals of R. Then
be the collection of all fuzzy k-ideals of R. Then 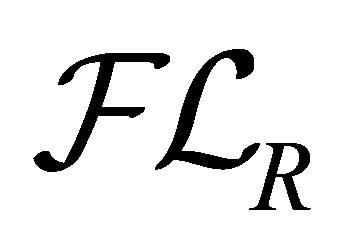 is a lattice (ordered by ≤) under the k-sum and k-product of fuzzy k-ideals.
is a lattice (ordered by ≤) under the k-sum and k-product of fuzzy k-ideals.
We show that 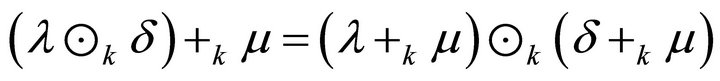 for all
for all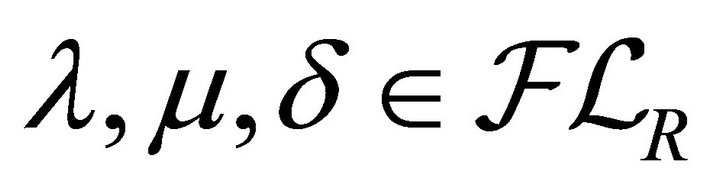 . Let
. Let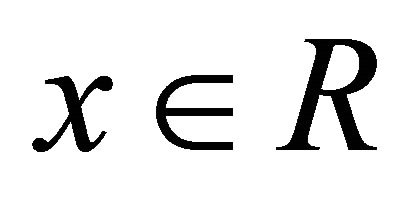 , then
, then
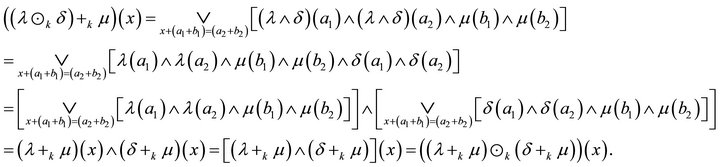
So, 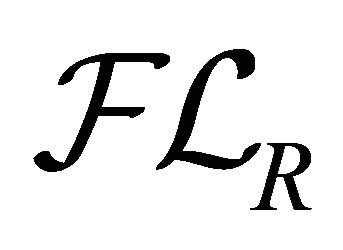 is a distributive lattice.
is a distributive lattice.
The converse is obvious.
5. Prime k-Ideals
A proper (left, right) k-ideal P of R is called prime if for any (left, right) k-ideals A, B of R, 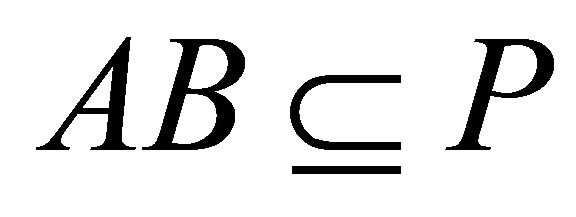 implies
implies 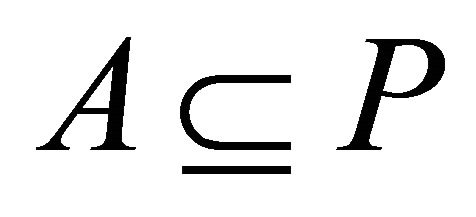 or
or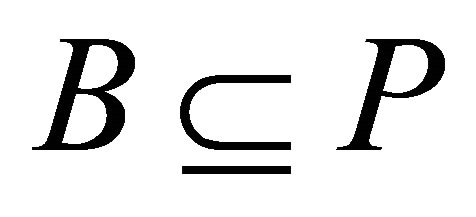 . A proper (left, right) k-ideal P of R is called irreducible if for any (left, right) k-ideals A, B of R,
. A proper (left, right) k-ideal P of R is called irreducible if for any (left, right) k-ideals A, B of R, 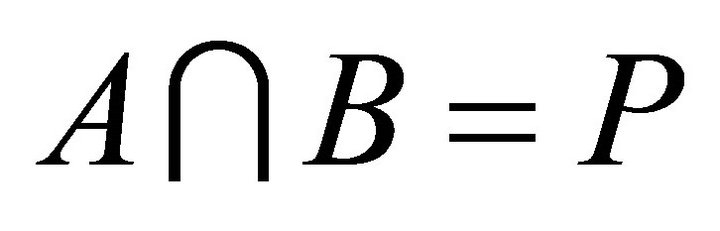 implies
implies 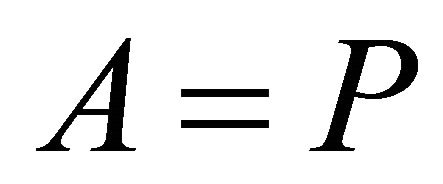 or
or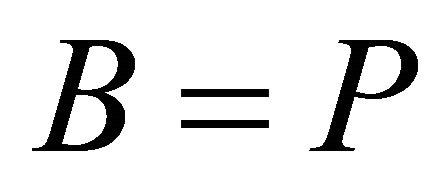 . By analogy a non-constant fuzzy k-ideal
. By analogy a non-constant fuzzy k-ideal ![]() of R is called prime (in the first sense) if for any fuzzy k-ideals
of R is called prime (in the first sense) if for any fuzzy k-ideals![]() ,
,  of R,
of R, 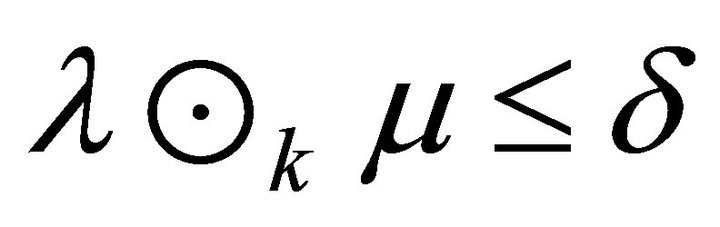 implies
implies  or
or , and irreducible if
, and irreducible if  implies
implies 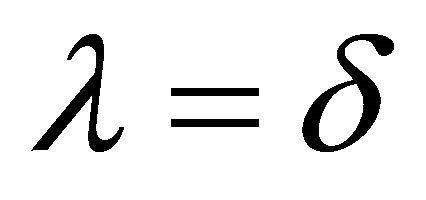 or
or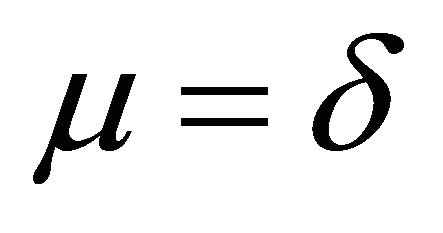 .
.
5.1. Theorem
A left (right) k-ideal P of a hemiring R with identity is prime if and only if for all  from
from 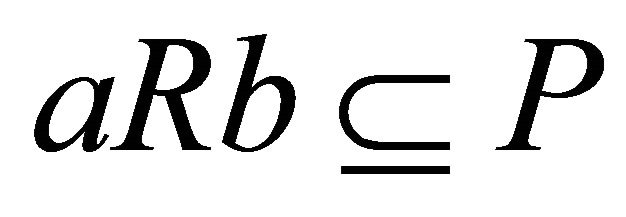 it follows
it follows 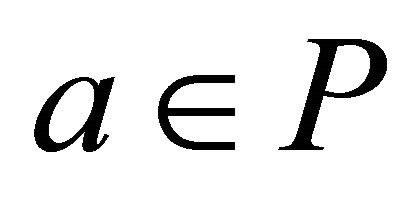 or
or .
.
Proof. Assume that P is a prime left k-ideal of R and
 for some
for some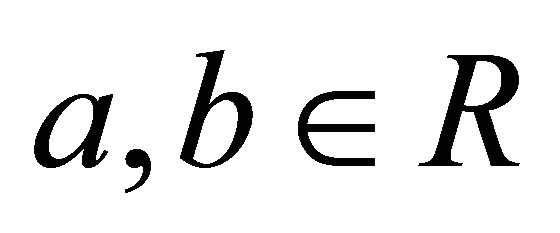 . Obviously,
. Obviously,  and
and  are left k-ideals of R generated by a and b, respectively. So,
are left k-ideals of R generated by a and b, respectively. So, 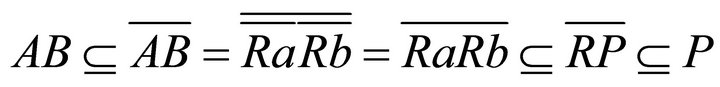 and consequently
and consequently  or
or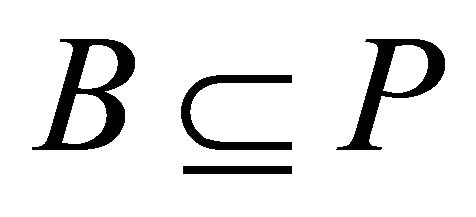 . If
. If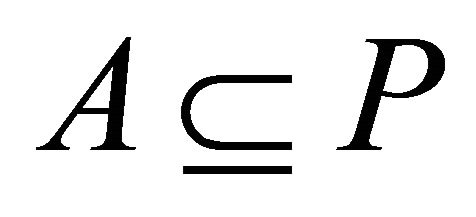 , then
, then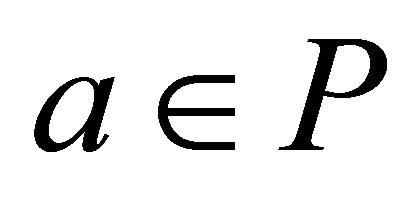 . If
. If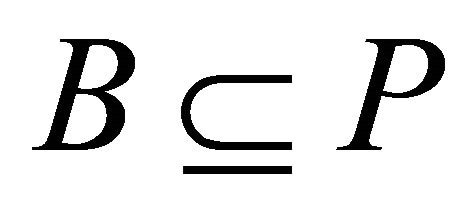 , then
, then .
.
The converse is obvious. □
5.2. Corollary
A k-ideal P of a hemiring R with identity is prime if and only if for all 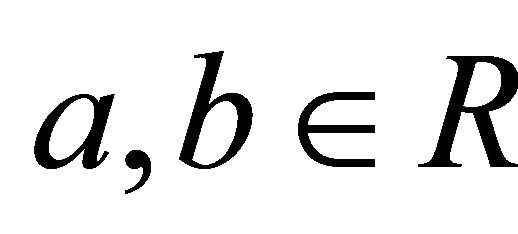 from
from 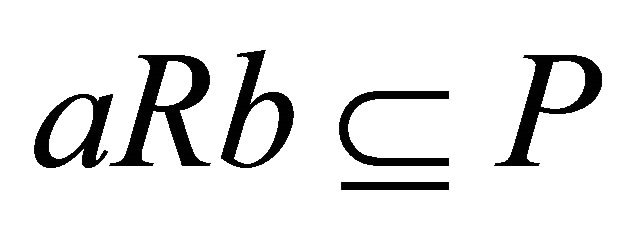 it follows
it follows  or
or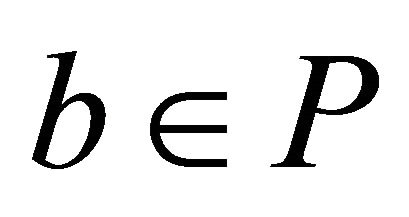 .
.
5.3. Corollary
A k-ideal P of a commutative hemiring R with identity is prime if and only if for all 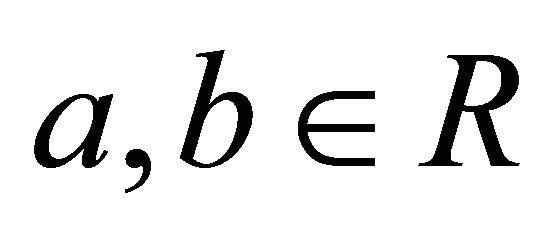 from
from  it follows
it follows 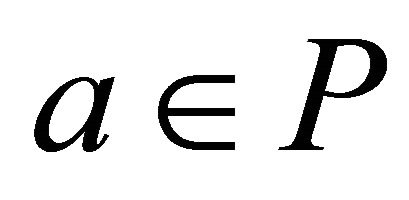 or
or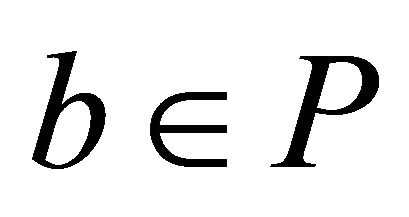 .
.
The result expressed by Corollary 5.3, suggests the following definition of prime fuzzy k-ideals.
5.4. Definition
A non-constant fuzzy k-ideal ![]() of R is called prime (in the second sense) if for all
of R is called prime (in the second sense) if for all 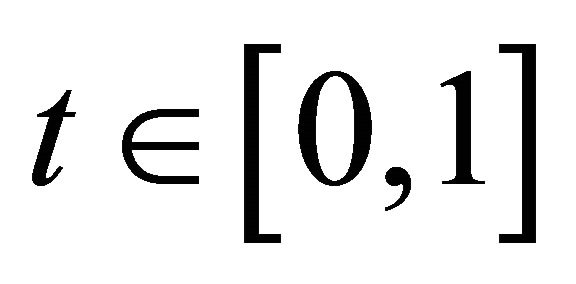 and
and 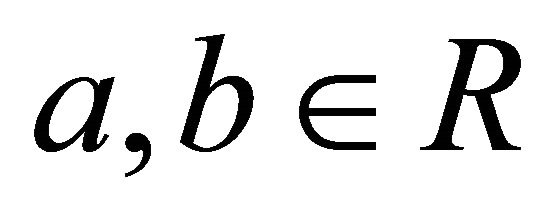 the following condition is satisfied:
the following condition is satisfied:
if  for every
for every  then
then  or
or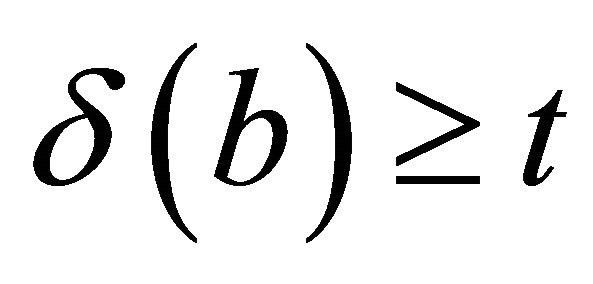 .
.
In other words, a non-constant fuzzy k-ideal ![]() is prime if from the fact that
is prime if from the fact that  for every
for every  it follows
it follows  or
or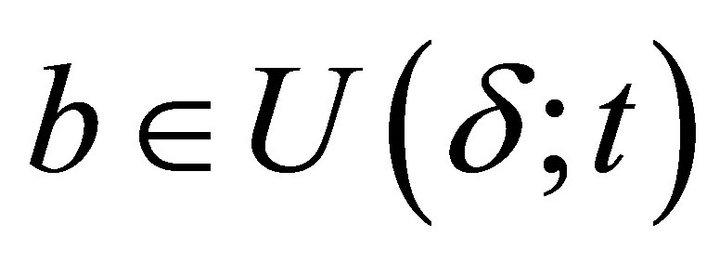 . It is clear that any fuzzy k-ideal is prime in the first sense is prime in the second sense. The converse is not true.
. It is clear that any fuzzy k-ideal is prime in the first sense is prime in the second sense. The converse is not true.
5.5. Example
In an ordinary hemiring of natural numbers the set of even numbers forms a k-ideal. A fuzzy set

is a fuzzy k-ideal of this hemiring. It is prime in the second sense but it is not prime in the first sense.
5.6. Theorem
A non-constant fuzzy k-ideal ![]() of a hemiring R with identity is prime in the second sense if and only if each its proper level set
of a hemiring R with identity is prime in the second sense if and only if each its proper level set  is a prime k-ideal of R.
is a prime k-ideal of R.
Proof. Suppose ![]() is a prime fuzzy k-ideal of R in the second sense and let
is a prime fuzzy k-ideal of R in the second sense and let 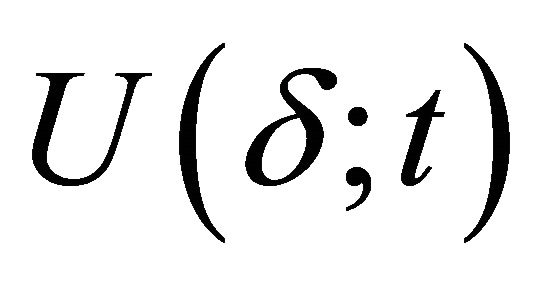 be its arbitrary proper level set, i.e.,
be its arbitrary proper level set, i.e.,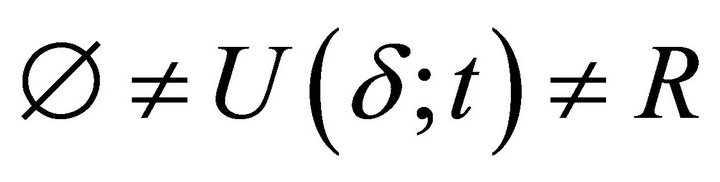 . If
. If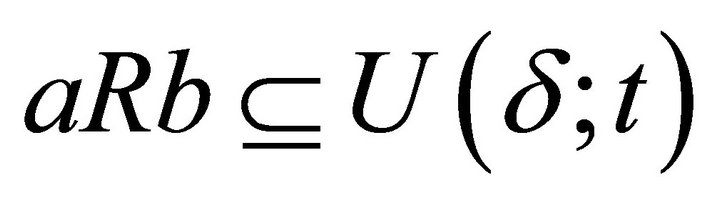 , then
, then 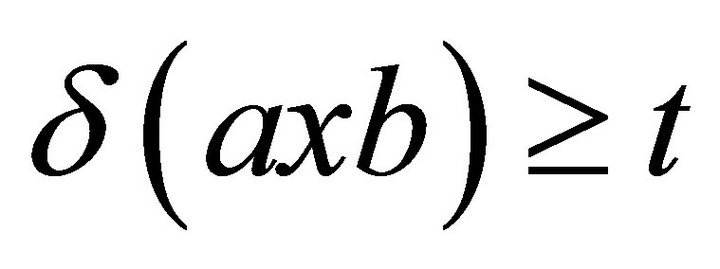 for every
for every . Hence
. Hence 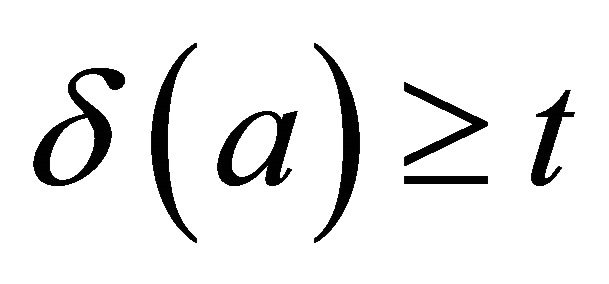 or
or 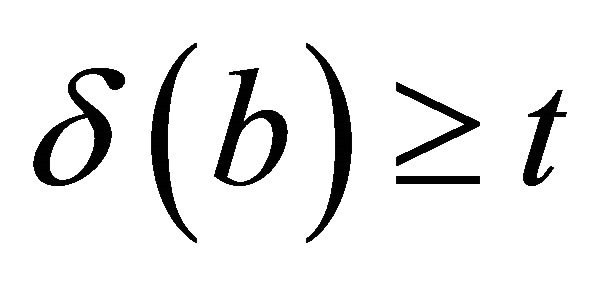 , i.e.,
, i.e., 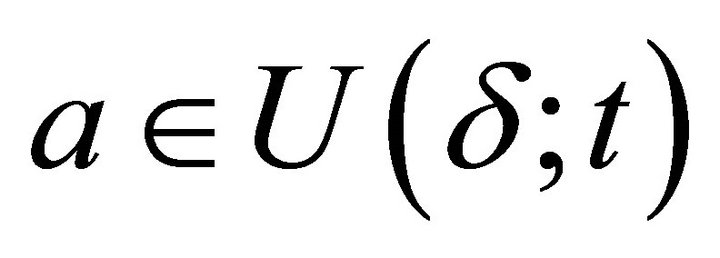 or
or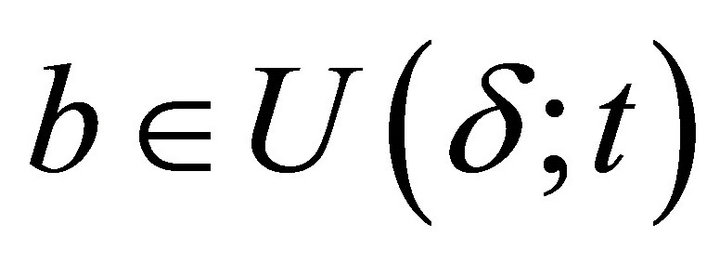 , which, by Corollary 5.3, means that
, which, by Corollary 5.3, means that 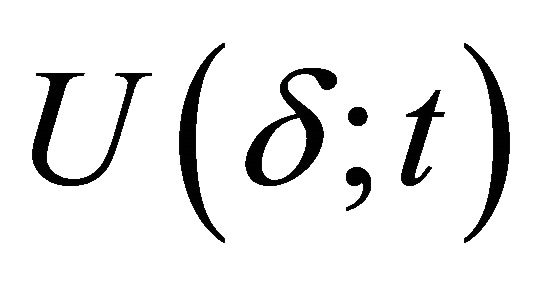 is a prime k-ideal of R.
is a prime k-ideal of R.
To prove the converse, consider a non-constant fuzzy k-ideal ![]() of R. If it is not prime then there exist a,
of R. If it is not prime then there exist a, 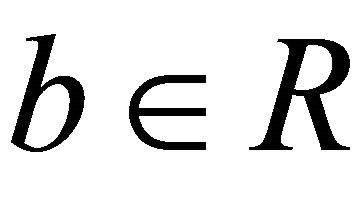 such that
such that 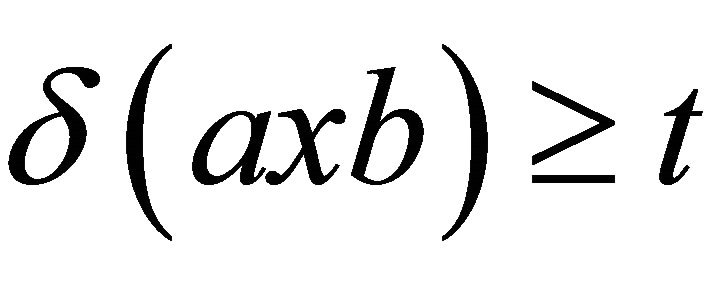 for all
for all , but
, but  and
and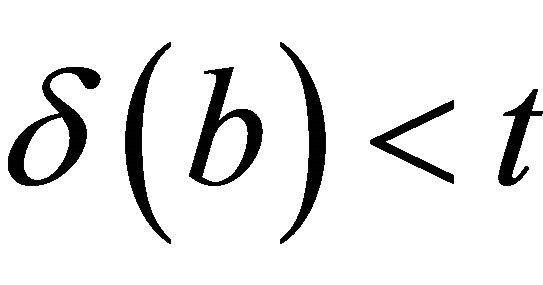 . Thus,
. Thus,  , but
, but 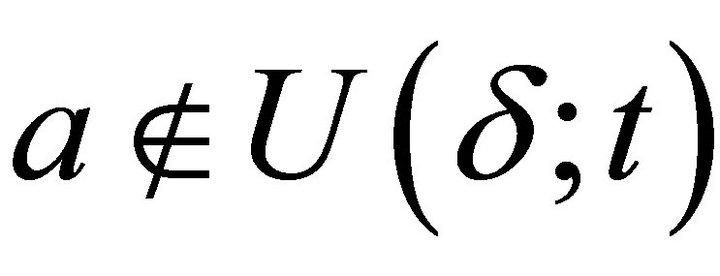 and
and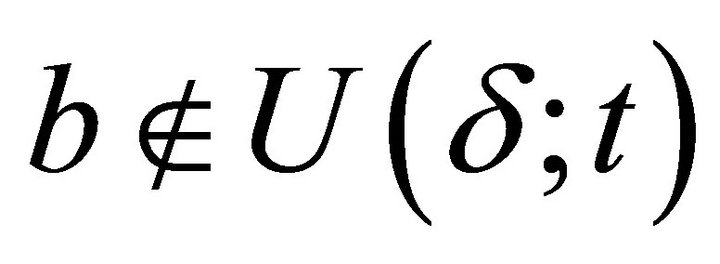 . Therefore
. Therefore  is not prime, which is a contradiction. Hence
is not prime, which is a contradiction. Hence ![]() is a prime fuzzy k-ideal in the second sense.
is a prime fuzzy k-ideal in the second sense.
5.7. Corollary
The fuzzy set  defined in Proposition 2.8, is a prime fuzzy k-ideal of R (with identity) in the second sense if and only if A is a prime k-ideal of R.
defined in Proposition 2.8, is a prime fuzzy k-ideal of R (with identity) in the second sense if and only if A is a prime k-ideal of R.
In view of the Transfer Principle the second definition of prime fuzzy k-ideal is better. Therefore fuzzy k-ideals which are prime in the first sense will be called k-prime.
5.8. Proposition
A non-constant fuzzy k-ideal ![]() of a commutative hemiring R with identity is prime if and only if
of a commutative hemiring R with identity is prime if and only if 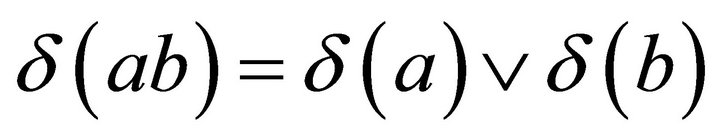 for all
for all .
.
Proof. Let ![]() be a non-constant fuzzy k-ideal of a commutative hemiring R with identity. If
be a non-constant fuzzy k-ideal of a commutative hemiring R with identity. If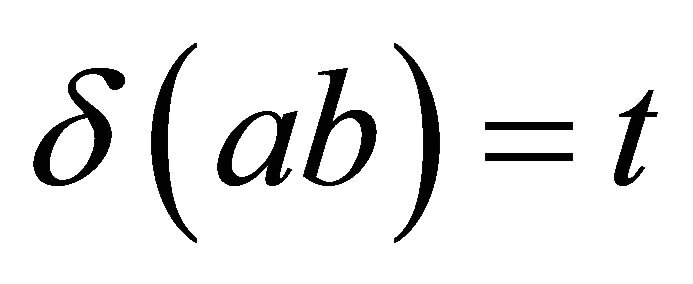 , then for every
, then for every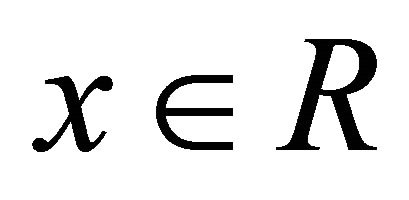 , we have
, we have
 . Thus
. Thus 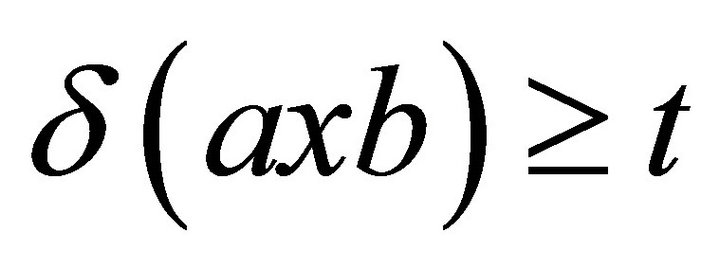 for every
for every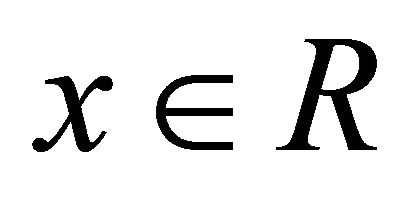 , which implies
, which implies  or
or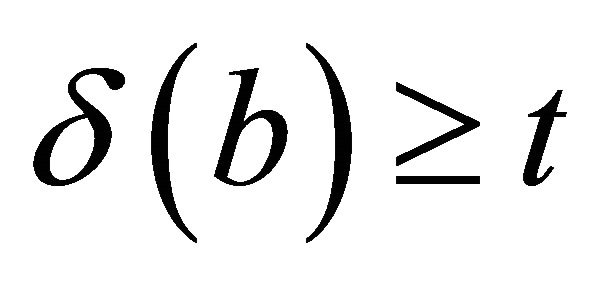 . If
. If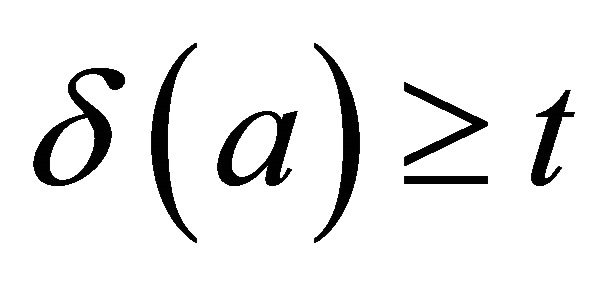 , then
, then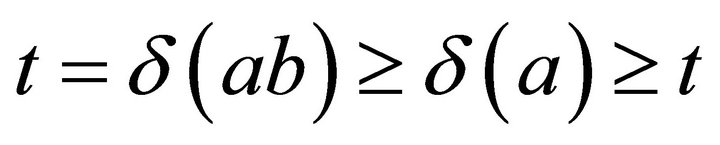 , whence
, whence 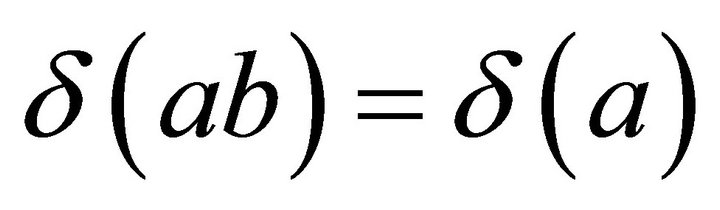 . If
. If , then, as in the previous case,
, then, as in the previous case,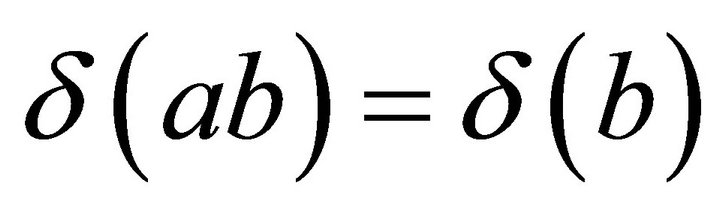 . So,
. So,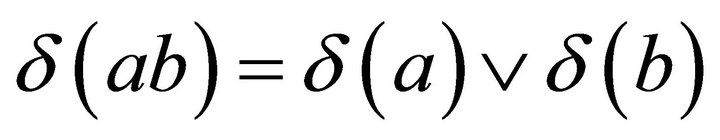 .
.
Conversely, assume that  for all
for all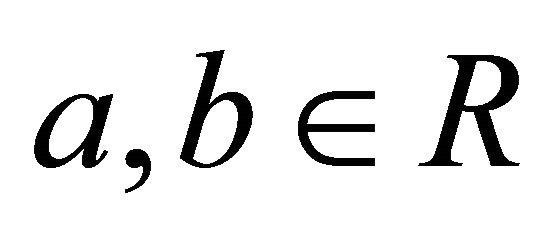 . If
. If 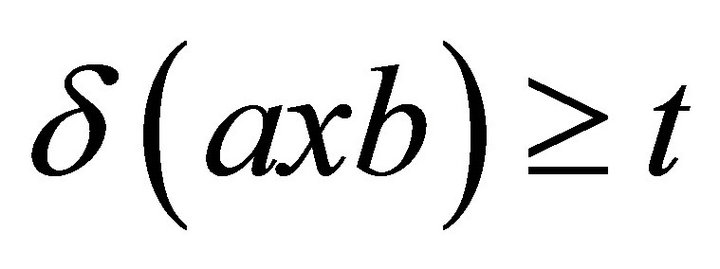 for every
for every , then replacing
, then replacing ![]() by the identity of R, we obtain
by the identity of R, we obtain . Thus
. Thus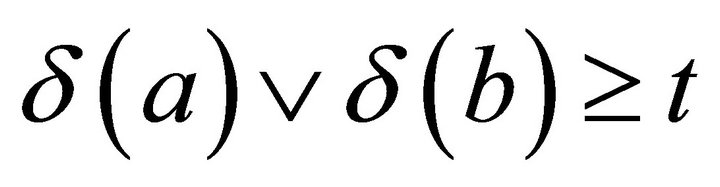 , i.e.,
, i.e., 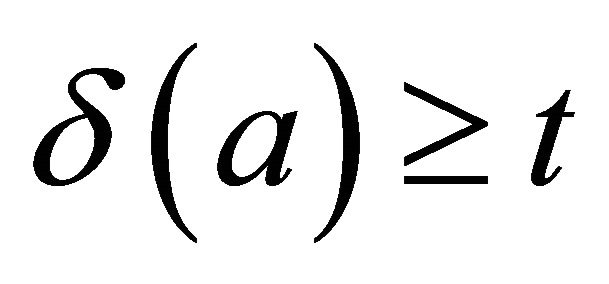 or
or , which means that
, which means that ![]() is prime. □
is prime. □
5.9. Theorem
Every proper k-ideal of a hemiring R is contained in some proper irreducible k-ideal of R.
Proof. Let P be a proper k-ideal of R such that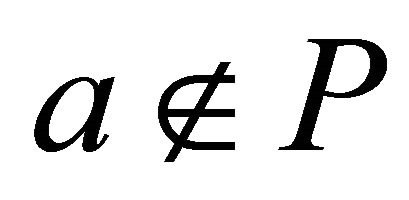 . Let
. Let 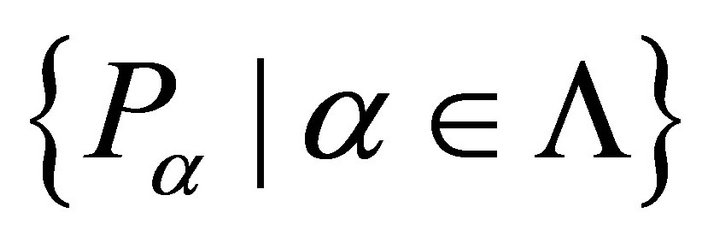 be a family of all proper k-ideals of R containing P and not containing a. By Zorn’s Lemma, this family contains a maximal element, say M. This maximal element is an irreducible k-ideal. Indeed, let
be a family of all proper k-ideals of R containing P and not containing a. By Zorn’s Lemma, this family contains a maximal element, say M. This maximal element is an irreducible k-ideal. Indeed, let 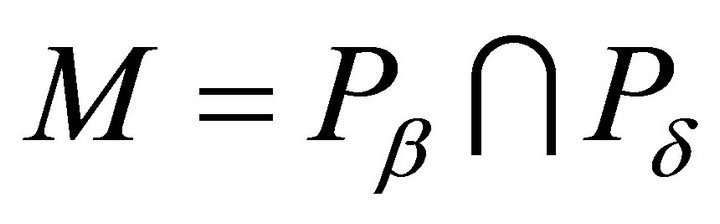 for some k-ideals
for some k-ideals 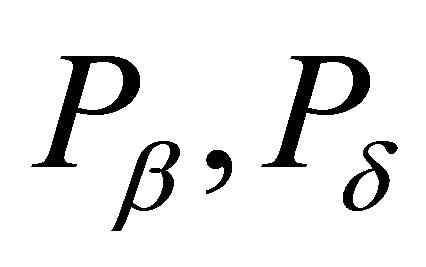 of R. If M is a proper subset of
of R. If M is a proper subset of 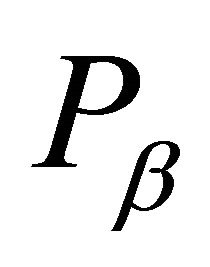 and
and , then, according to the maximality of M, we have
, then, according to the maximality of M, we have 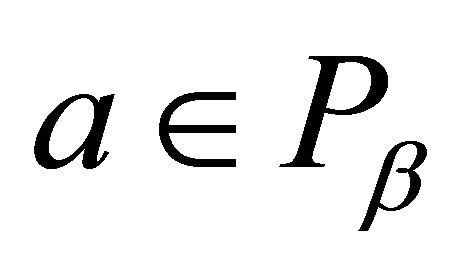 and
and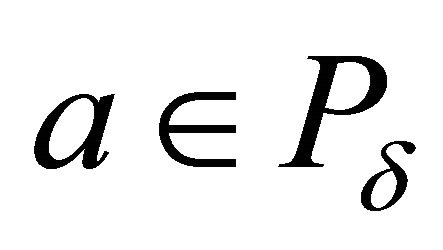 . Hence
. Hence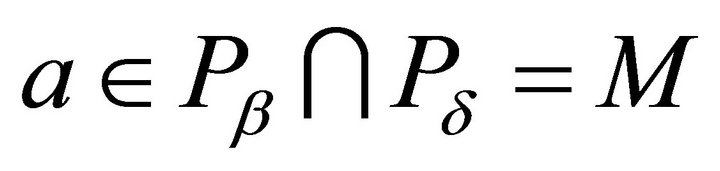 , which is impossible. Thus, either
, which is impossible. Thus, either
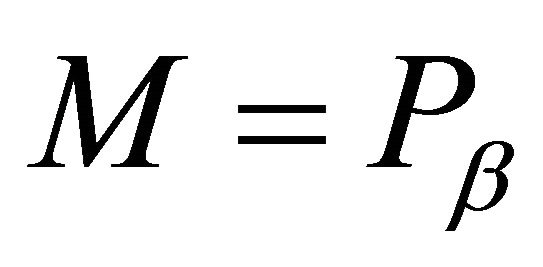 or
or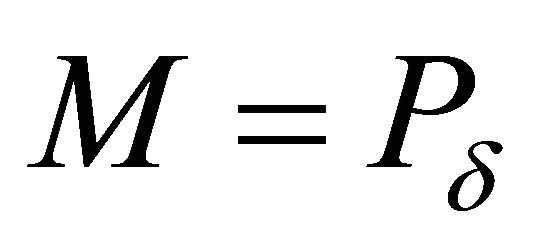 . □
. □
5.10. Theorem
If all k-ideals of R are idempotent, then a k-ideal P of R is irreducible if and only if it is prime.
Proof. Assume that all k-ideals of R are idempotent. Let P be a fixed irreducible k-ideal. If 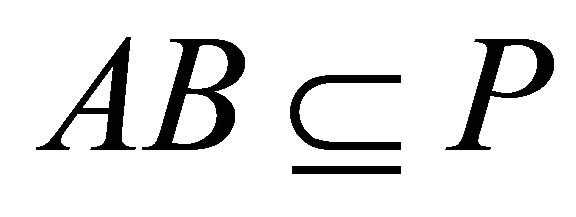 for some k-ideals A, B of R, then by Proposition 4.1,
for some k-ideals A, B of R, then by Proposition 4.1,
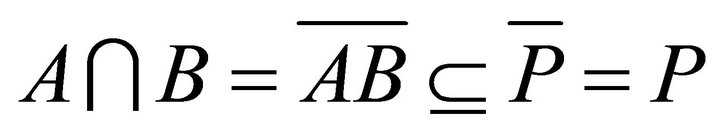 . Thus
. Thus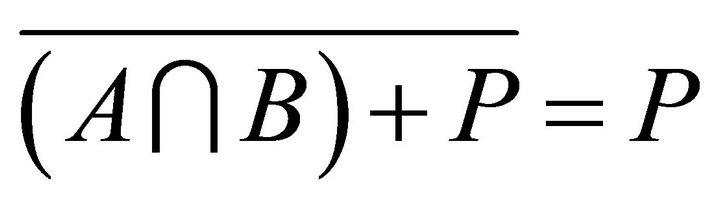 . Since
. Since  is a distributive lattice, so
is a distributive lattice, so
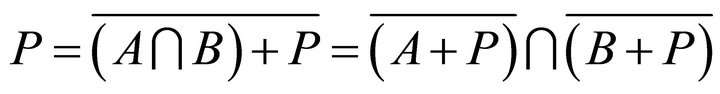 .
.
So either 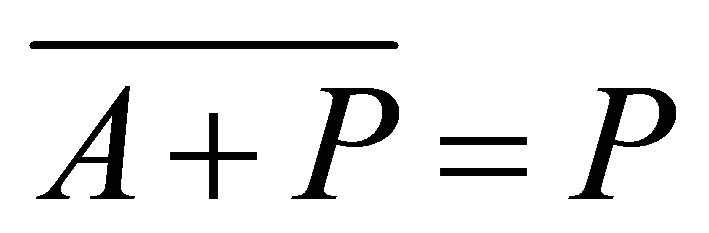 or
or , that is either
, that is either  or
or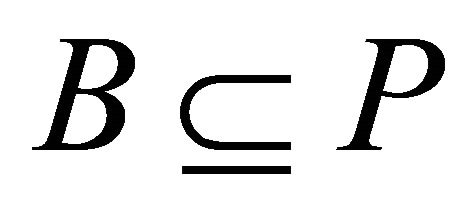 .
.
Conversely, if a k-ideal P is prime and  for some
for some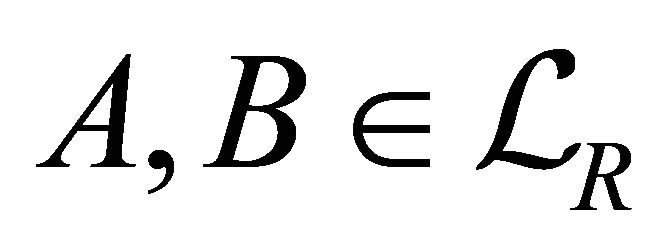 , then
, then . Thus
. Thus  or
or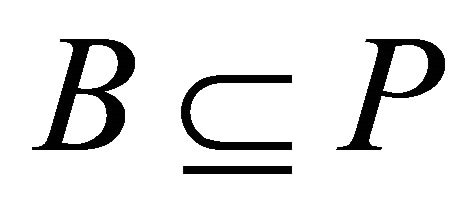 . But
. But 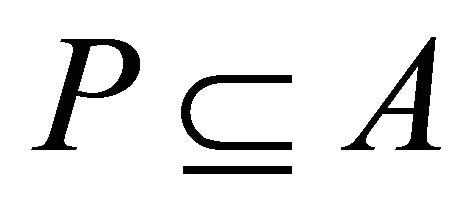 and
and . Hence
. Hence 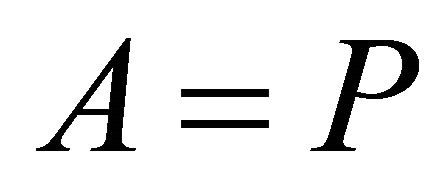 or
or . □
. □
5.11. Corollary
Let R be a hemiring in which all k-ideals are idempotent. Then each proper k-ideal of R is contained in some proper prime k-ideal.
5.12. Theorem
Let R be a hemiring in which all fuzzy k-ideals are idempotent. Then a fuzzy k-ideal of R is irreducible if and only if it is k-prime.
Proof. Assume that all fuzzy k-ideals of R are idempotent and let ![]() be an arbitrary irreducible fuzzy k-ideal of R. We prove that it is k-prime. If
be an arbitrary irreducible fuzzy k-ideal of R. We prove that it is k-prime. If 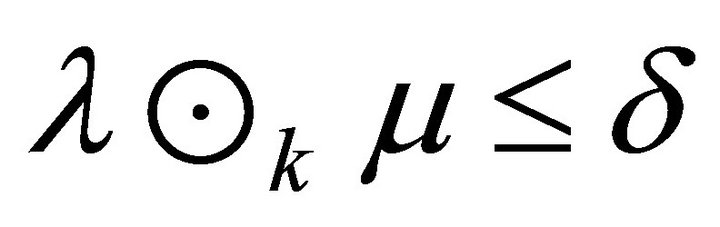 for some fuzzy k-ideals
for some fuzzy k-ideals ![]() of R then also
of R then also . Since the set
. Since the set 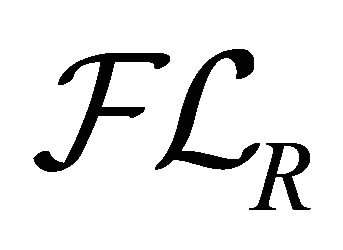 of all fuzzy k-ideals of R is a distributive lattice, we have
of all fuzzy k-ideals of R is a distributive lattice, we have  . Thus
. Thus 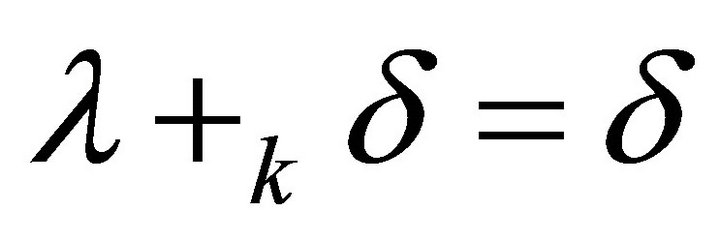 or
or . Thus
. Thus 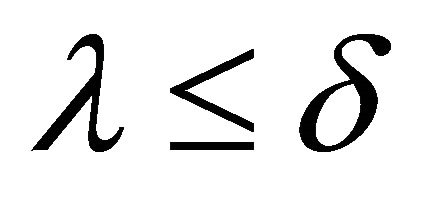 or
or . This proves that
. This proves that ![]() is k-prime.
is k-prime.
Conversely, if ![]() is a k-prime fuzzy k-ideal of R and
is a k-prime fuzzy k-ideal of R and 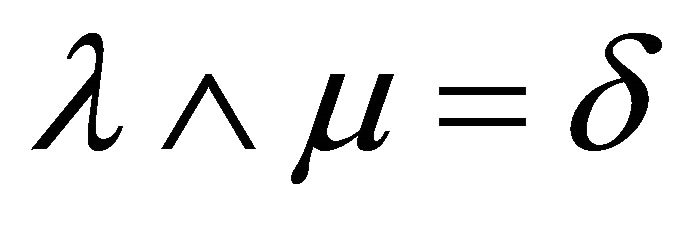 for some
for some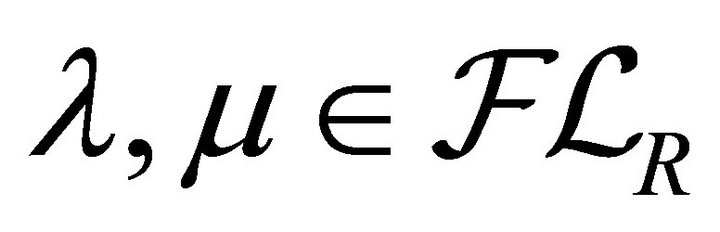 , then
, then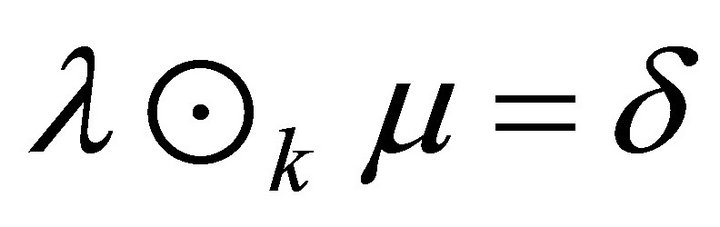 , which implies
, which implies 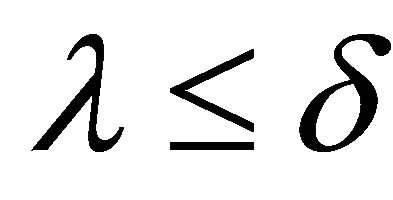 or
or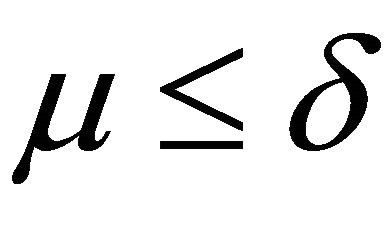 . Since
. Since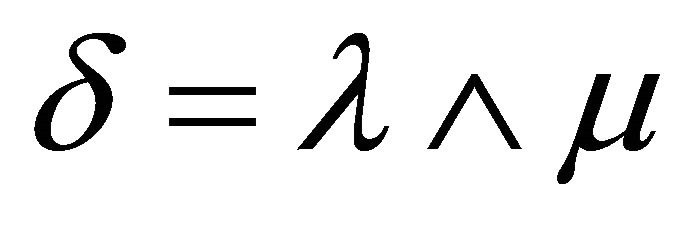 , so we have also
, so we have also  and
and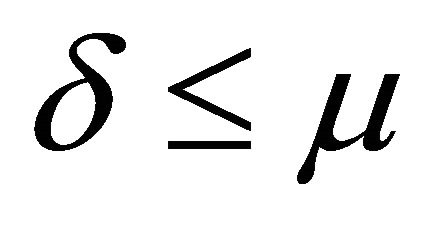 . Thus
. Thus 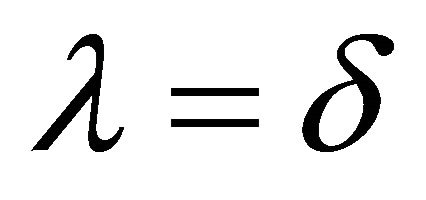 or
or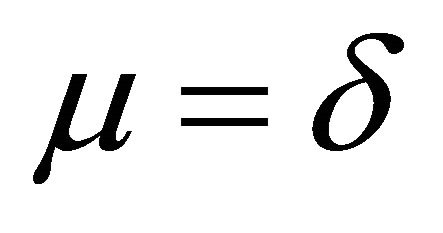 . So,
. So, ![]() is irreducible. □
is irreducible. □
5.13. Theorem
The following assertions for a hemiring R are equivalent:
1) Each k-ideal of R is idempotent.
2) Each proper k-ideal P of R is the intersection of all prime k-ideals of R which contain P.
Proof. 1) ® 2) Let P be a proper k-ideal of R and let 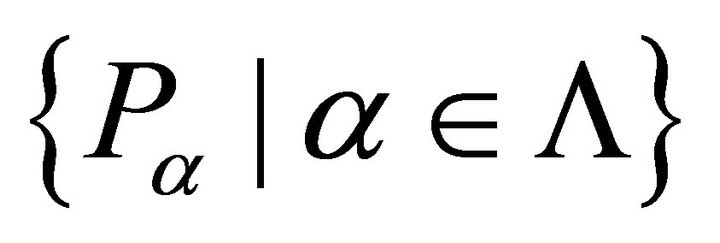 be the family of all prime k-ideals of R which contain P. Theorem 5.9, guarantees the existance of such ideals. Clearly
be the family of all prime k-ideals of R which contain P. Theorem 5.9, guarantees the existance of such ideals. Clearly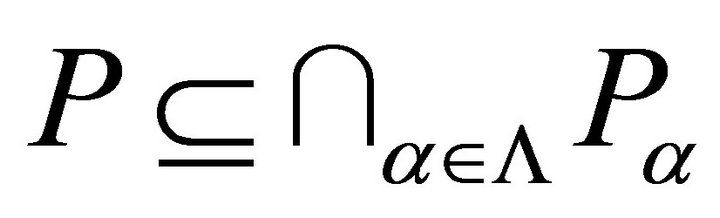 . If
. If 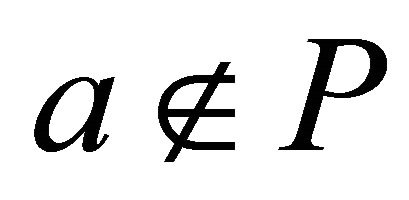 then by Theorem 5.9, there exists an irreducible k-ideal
then by Theorem 5.9, there exists an irreducible k-ideal 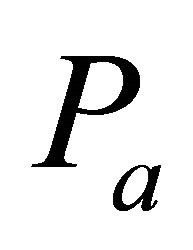 such that
such that  and
and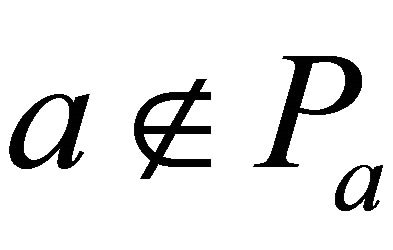 . By Theorem 5.10,
. By Theorem 5.10, 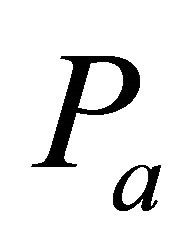 is prime. So there exists a prime k-ideal
is prime. So there exists a prime k-ideal 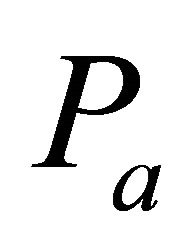 such that
such that 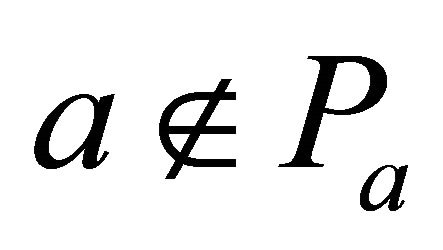 and
and . Hence
. Hence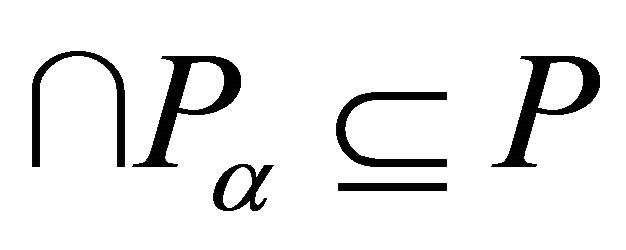 . Thus
. Thus .
.
2) ® 1) Assume that each k-ideal of R is the intersection of all prime k-ideals of R which contain it. Let A be a k-ideal of R. If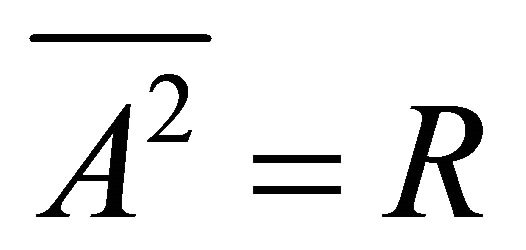 , then we have
, then we have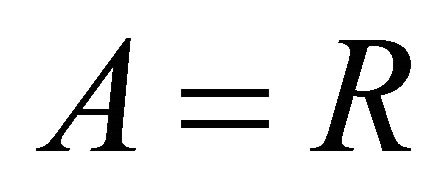 , which means that A is idempotent. If
, which means that A is idempotent. If 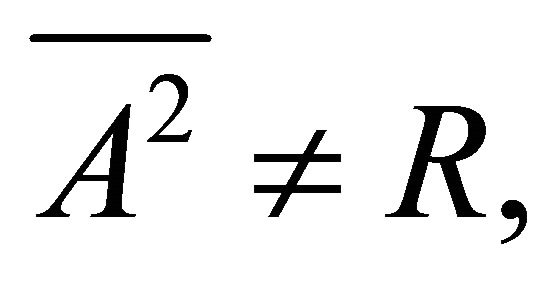 then
then  is a proper k-ideal of R and so it is the intersection of all prime k-ideals of R containing
is a proper k-ideal of R and so it is the intersection of all prime k-ideals of R containing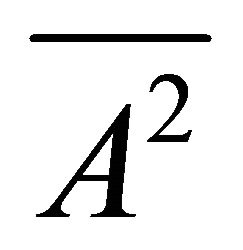 . Let
. Let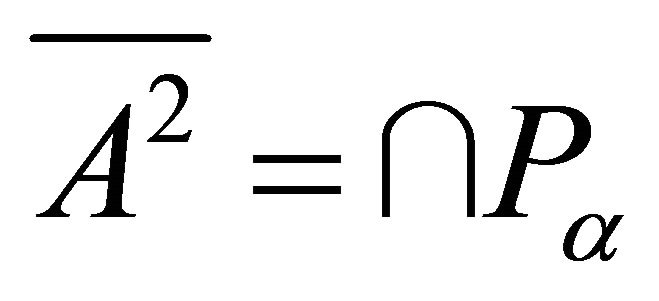 . Then
. Then  for each
for each![]() . Since
. Since  is prime, we have
is prime, we have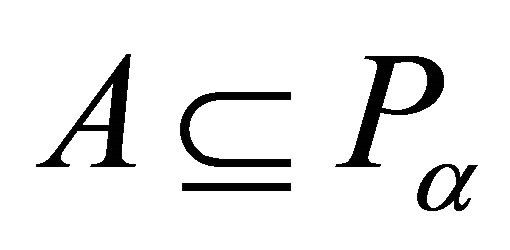 . Thus
. Thus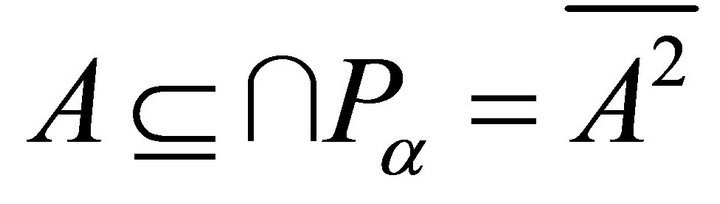 . But
. But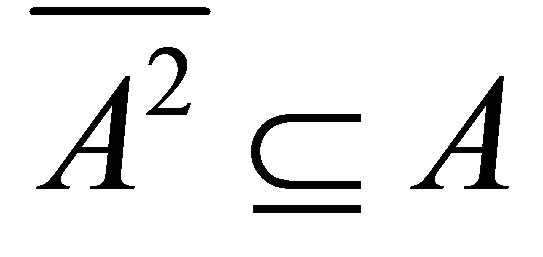 . Hence
. Hence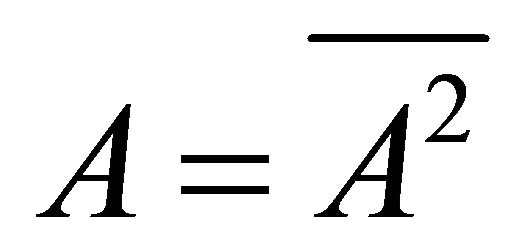 . □
. □
5.14. Lemma
Let R be a hemiring in which each fuzzy k-ideal is idempotent. If ![]() is a fuzzy k-ideal of R with
is a fuzzy k-ideal of R with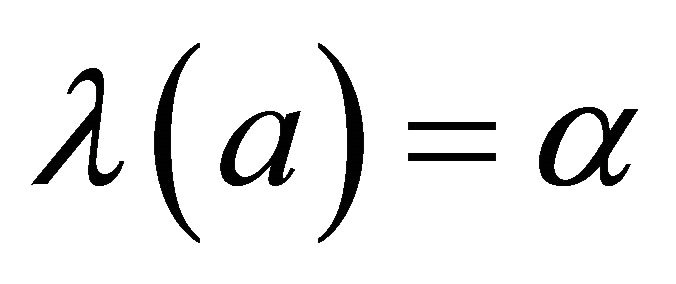 , where a is any element of R and
, where a is any element of R and , then there exists an irreducible k-prime fuzzy k-ideal
, then there exists an irreducible k-prime fuzzy k-ideal ![]() of R such that
of R such that 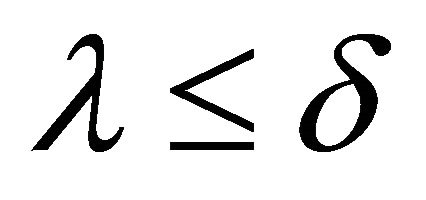 and
and .
.
Proof. Let ![]() be an arbitrary fuzzy k-ideal of R and
be an arbitrary fuzzy k-ideal of R and 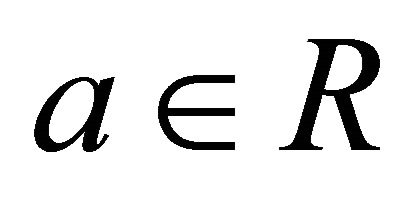 be fixed. Consider the following collection of fuzzy k-ideals of R
be fixed. Consider the following collection of fuzzy k-ideals of R
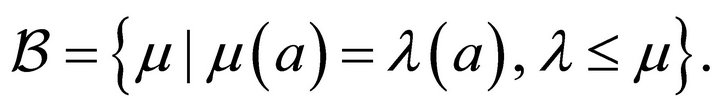
 is non-empty since
is non-empty since . Let
. Let  be a totally ordered subset of
be a totally ordered subset of  containing
containing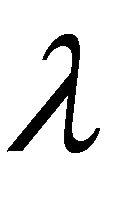 , say
, say .
.
We claim that 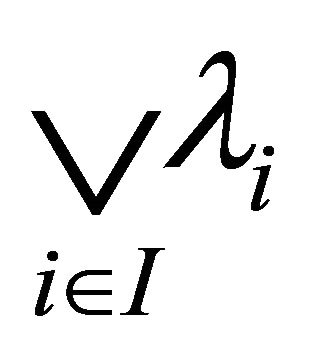 is a fuzzy k-ideal of R.
is a fuzzy k-ideal of R.
For any 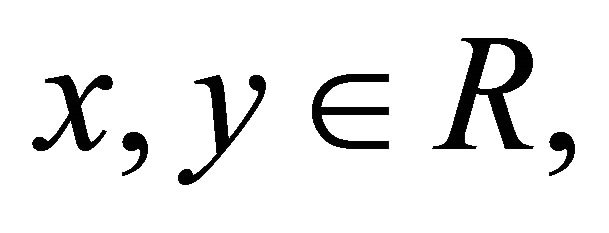 we have
we have

Similarly

and

for all . Thus
. Thus 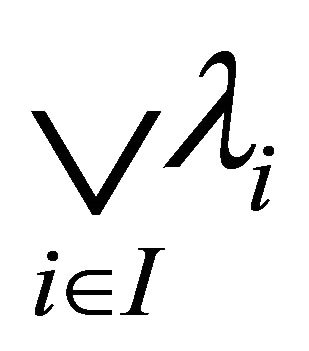 is a fuzzy ideal.
is a fuzzy ideal.
Now, let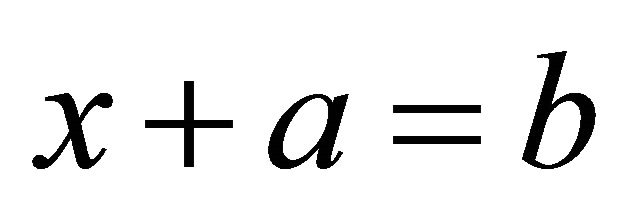 , where
, where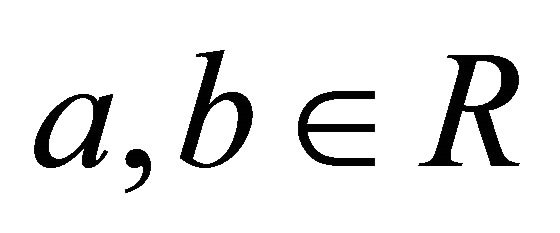 . Then
. Then
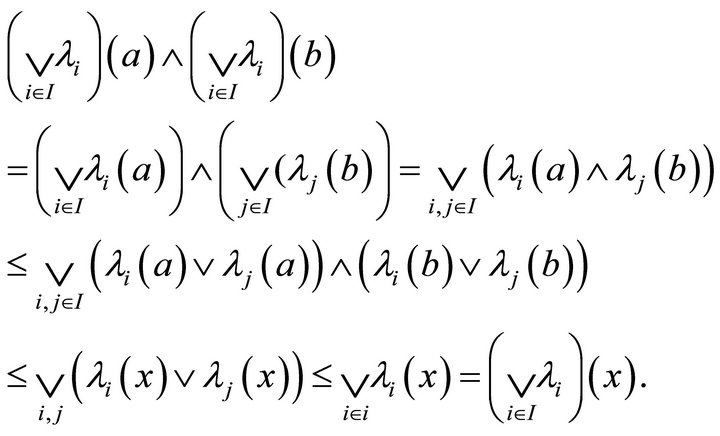
Thus 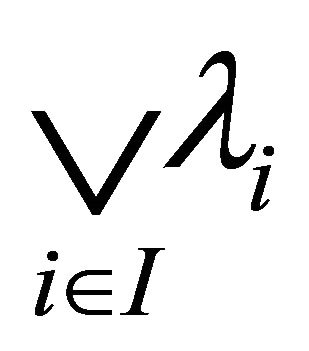 is a fuzzy k-ideal of R. Clearly
is a fuzzy k-ideal of R. Clearly 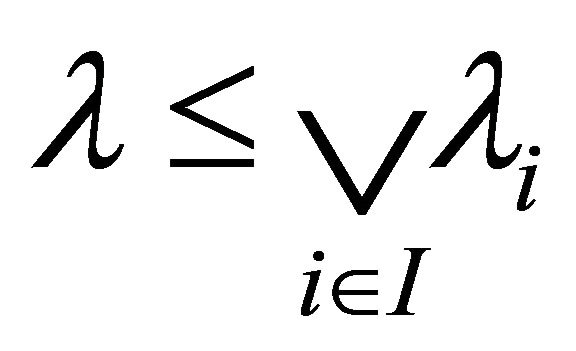 and
and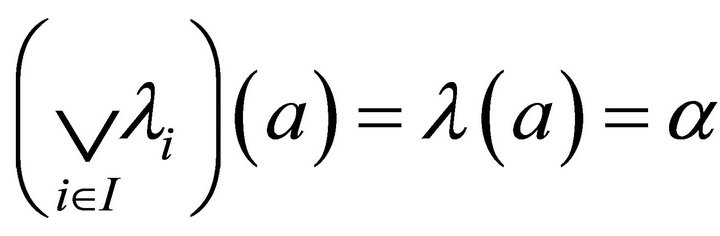 . Thus
. Thus  is the least upper bound of
is the least upper bound of . Hence by Zorn’s lemma there exists a fuzzy k-ideal
. Hence by Zorn’s lemma there exists a fuzzy k-ideal ![]() of R which is maximal with respect to the property that
of R which is maximal with respect to the property that 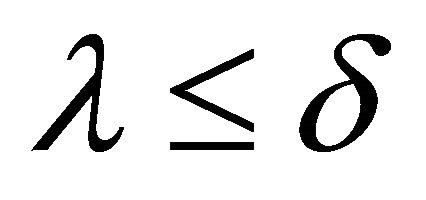 and
and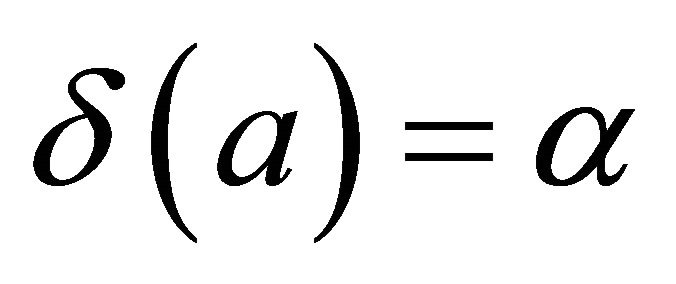 .
.
We will show that ![]() is an irreducible fuzzy k-ideal of R. Let
is an irreducible fuzzy k-ideal of R. Let , where
, where 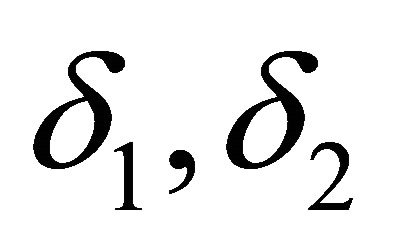 are fuzzy k-ideals of R. Then
are fuzzy k-ideals of R. Then 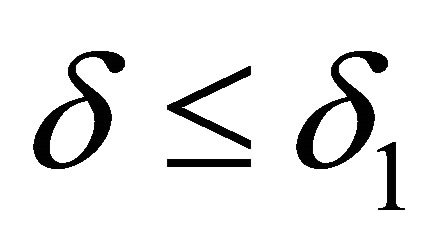 and
and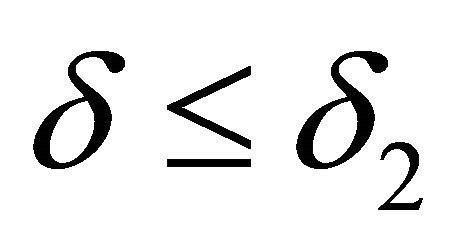 . We claim that either
. We claim that either 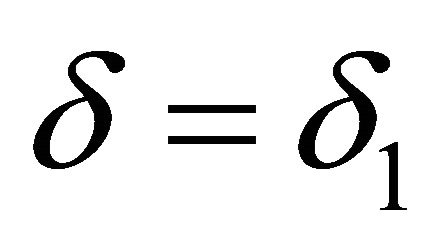 or
or . Suppose
. Suppose 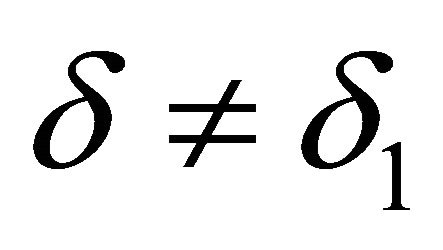 and
and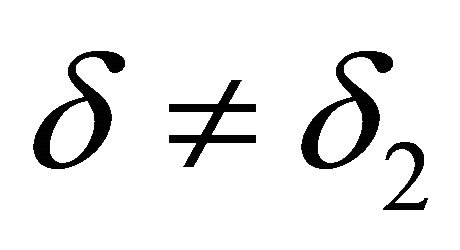 . Since
. Since  is maximal with respect to the property that
is maximal with respect to the property that  and since
and since 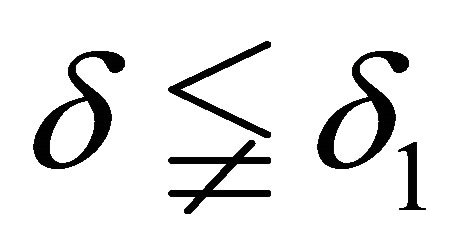 and
and , so
, so 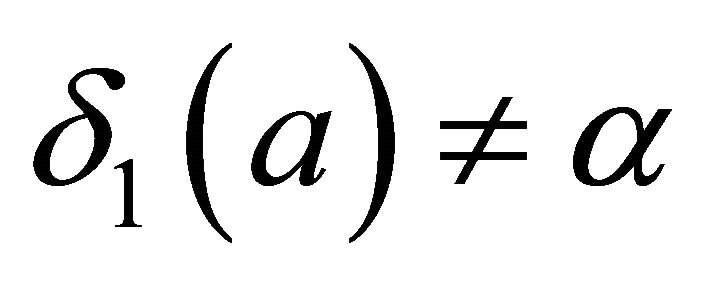 and
and . Hence
. Hence

which is impossible. Hence 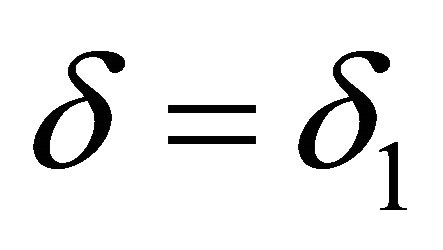 or
or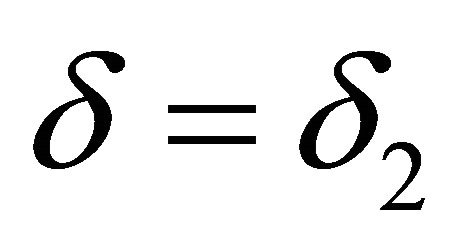 . Thus
. Thus ![]() is an irreducible fuzzy k-ideal of R. By Theorem 5.12,
is an irreducible fuzzy k-ideal of R. By Theorem 5.12, ![]() is k-prime. □
is k-prime. □
5.15. Theorem
Each fuzzy k-ideal of R is idempotent if and only if each fuzzy k-ideal of R is the intersection of those k-prime fuzzy k-ideals of R which contain it.
Proof. Suppose each fuzzy k-ideal of R is idempotent. Let ![]() be a fuzzy k-ideal of R and let
be a fuzzy k-ideal of R and let 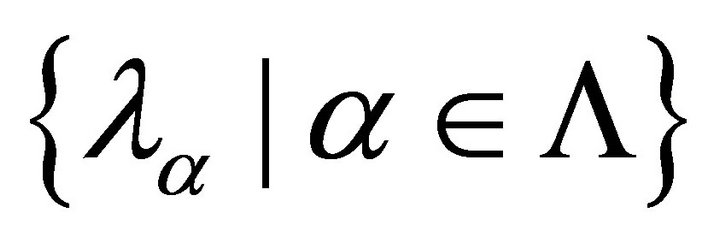 be the family of all k-prime fuzzy k-ideals of R which contain
be the family of all k-prime fuzzy k-ideals of R which contain![]() . Obviously
. Obviously . We now show that
. We now show that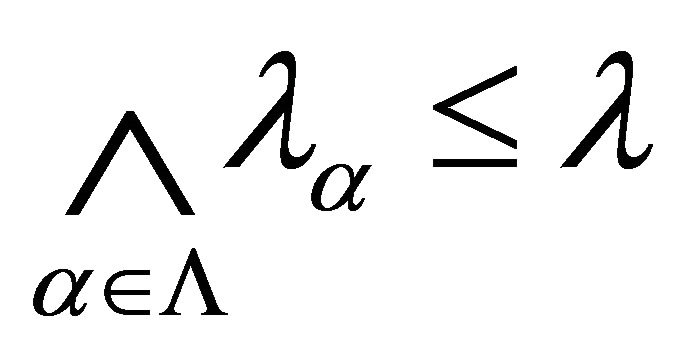 . Let a be an arbitrary element of R. Thenby Lemma 5.14, there exists an irreducible k-prime fuzzy k-ideal
. Let a be an arbitrary element of R. Thenby Lemma 5.14, there exists an irreducible k-prime fuzzy k-ideal ![]() such that
such that 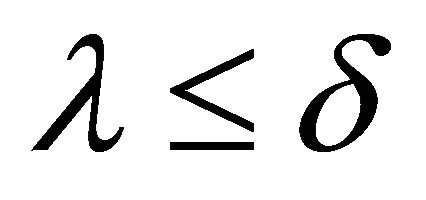 and
and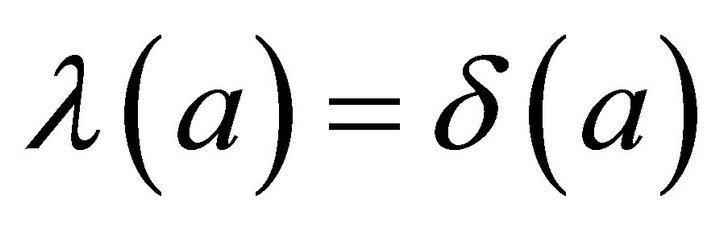 . Hence
. Hence
 and
and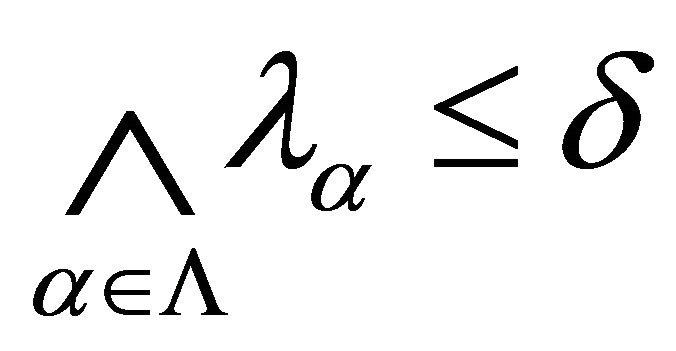 . So,
. So,
 . Thus
. Thus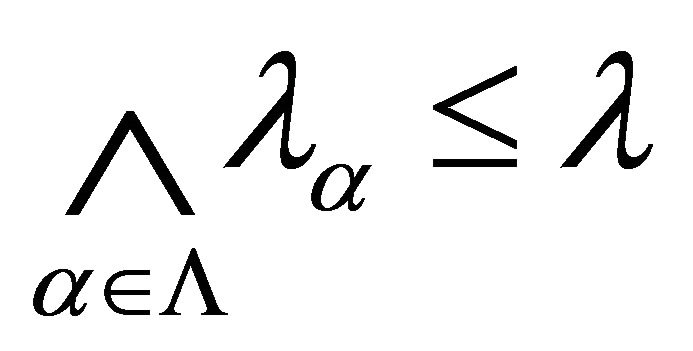 . Therefore
. Therefore .
.
Conversely, assume that each fuzzy k-ideal of R is the intersection of those k-prime fuzzy k-ideals of R which contain it. Let ![]() be a fuzzy k-ideal of R then
be a fuzzy k-ideal of R then 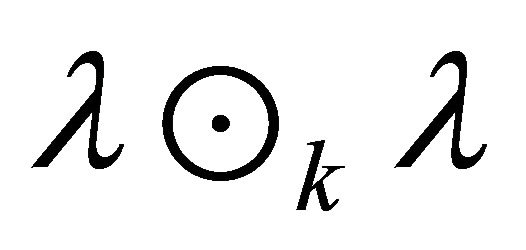
is also a fuzzy k-ideal of , so
, so 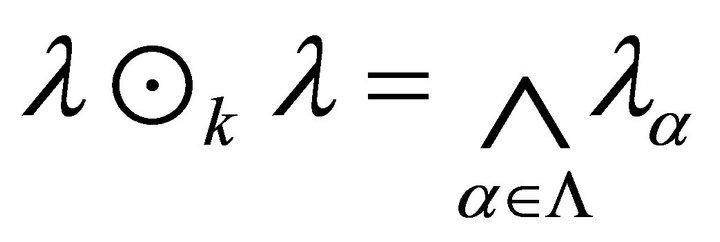 where
where
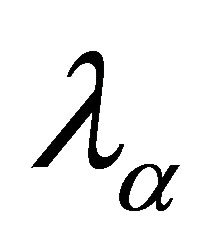 are k-prime fuzzy k-ideals of R. Thus each
are k-prime fuzzy k-ideals of R. Thus each 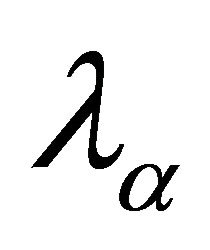 contains
contains , and hence
, and hence![]() . So
. So , but
, but
 always. Hence
always. Hence . □
. □
6. Semiprime k-Ideals
6.1. Definition
A proper (left, right) k-ideal A of R is called semiprime if for any (left, right) k-ideal B of R, 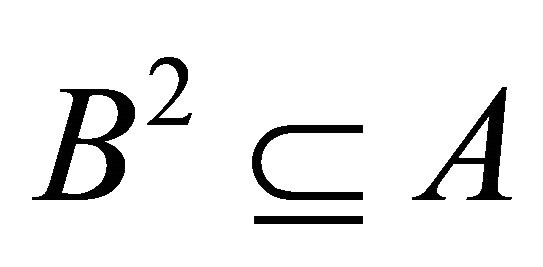 implies
implies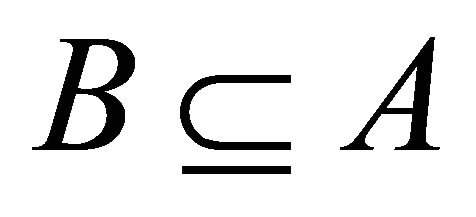 . Similarly, a non-constant fuzzy k-ideal
. Similarly, a non-constant fuzzy k-ideal ![]() of R is called semiprime if for any fuzzy k-ideal
of R is called semiprime if for any fuzzy k-ideal ![]() of R,
of R,  implies
implies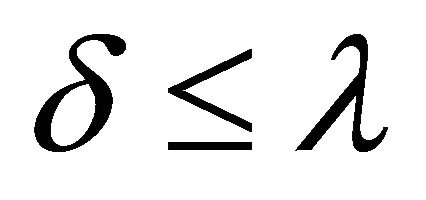 .
.
6.2. Theorem
A (left, right) k-ideal P of a hemiring R with identity is semiprime if and only if for every 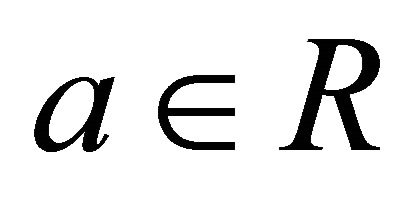 from
from  it follows
it follows .
.
Proof. Proof is similar to the proof of Theorem 5.1. □
6.3. Corollary
A k-ideal P of a commutative hemiring R with identity is semiprime if and only if for all 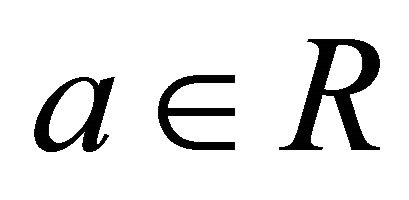 from
from 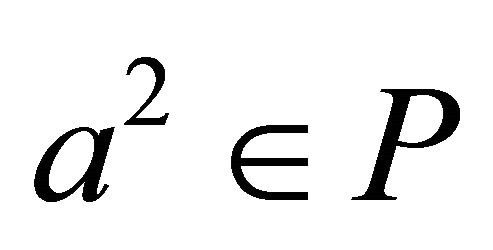 it follows
it follows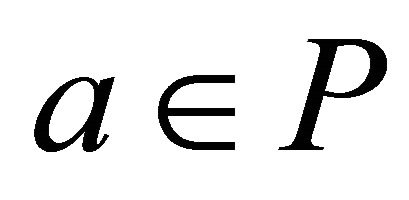 .
.
6.4. Theorem
The following assertions for a hemiring R are equivalent:
1) Each k-ideal of R is idempotent.
2) Each k-ideal of R is semiprime.
Proof. Suppose that each k-ideal of R is idempotent. Let A, B be k-ideals of R such that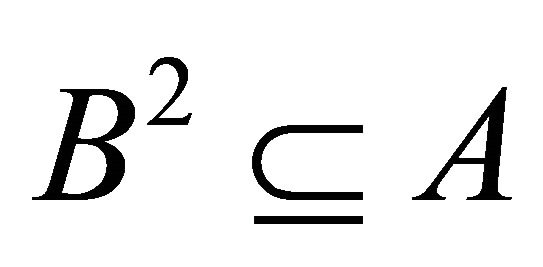 . Then
. Then
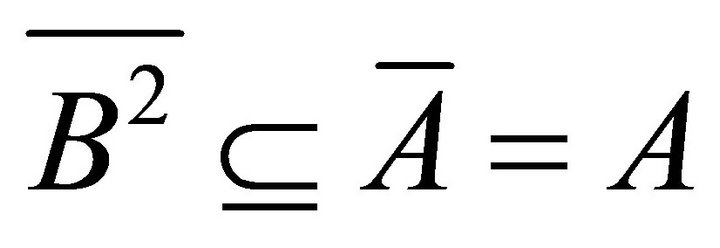 . By hypothesis
. By hypothesis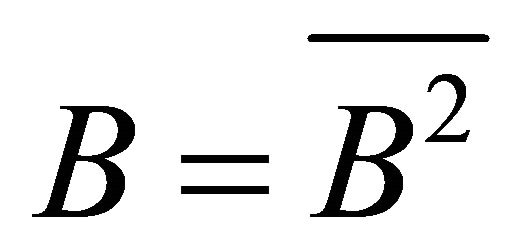 , so
, so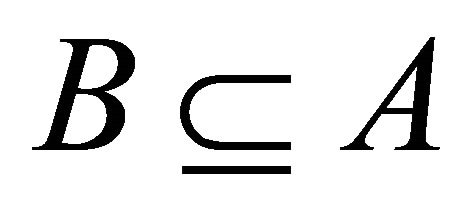 . Hence A is semiprime.
. Hence A is semiprime.
Conversely, assume that each k-ideal of R is semiprime. Let A be a k-ideal of R, then 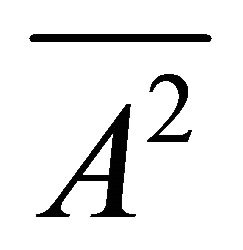 is a k-ideal of R. Also
is a k-ideal of R. Also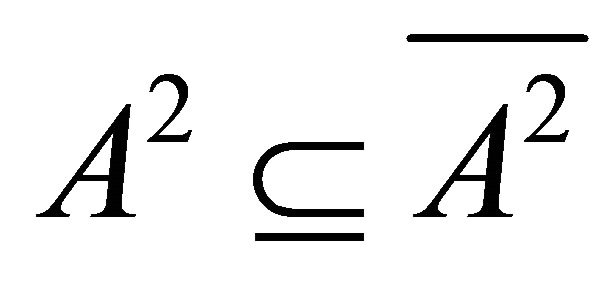 . Hence by hypothesis
. Hence by hypothesis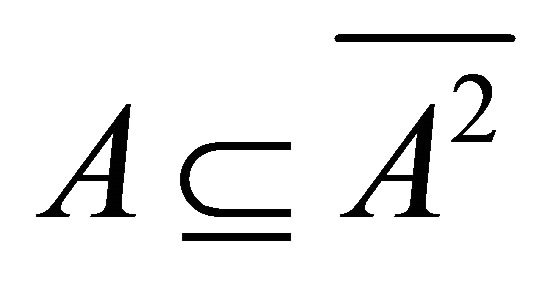 . But
. But
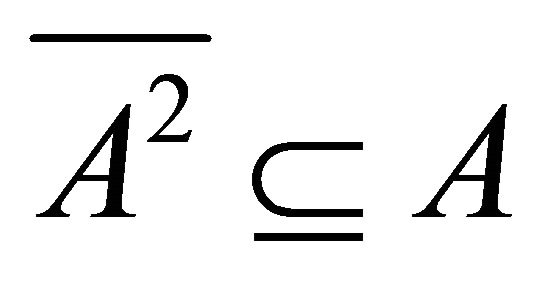 always. Hence
always. Hence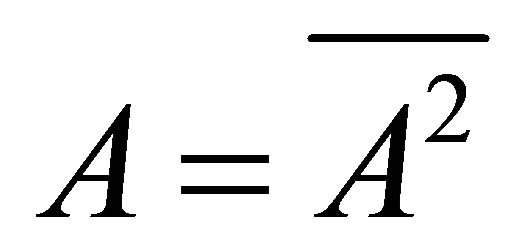 . □
. □
6.5. Theorem
Each fuzzy k-ideal of R is idempotent if and only if each fuzzy k-ideal of R is semiprime.
Proof. For any fuzzy k-ideal ![]() of R we have
of R we have 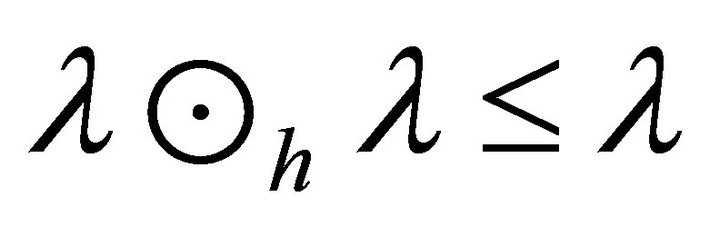 . If each fuzzy k-ideal of
. If each fuzzy k-ideal of  is semiprime, then
is semiprime, then  implies
implies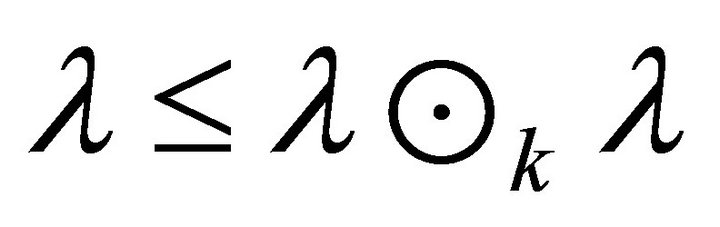 . Hence
. Hence 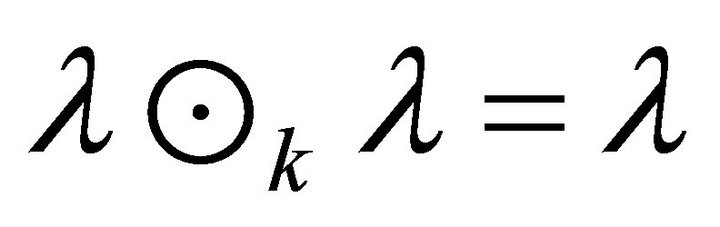 .
.
The converse is obvious. □
Theorem 6.2, suggest the following definition of semiprime fuzzy k-ideals.
6.6. Definition
A non-constant fuzzy k-ideal ![]() of R is called semiprime (in the second sense) if for all
of R is called semiprime (in the second sense) if for all  and
and  the following condition is satisfied:
the following condition is satisfied:
if 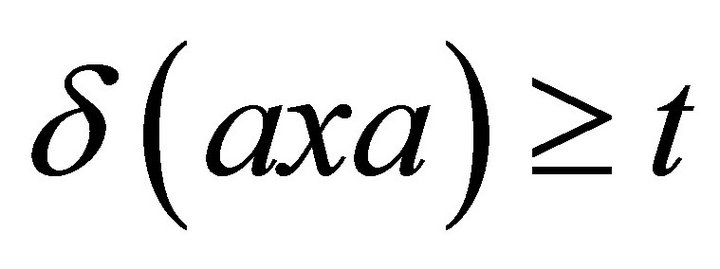 for every
for every 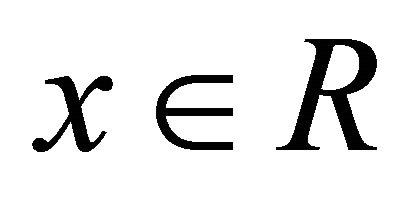 then
then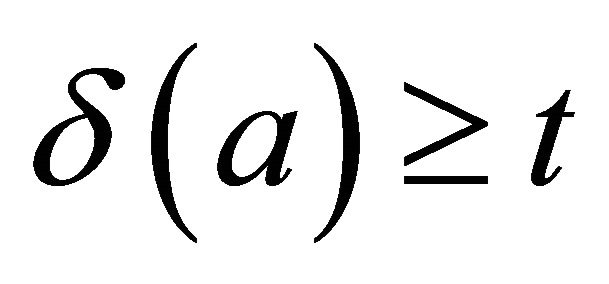 .
.
6.7. Theorem
A non-constant fuzzy k-ideal ![]() of R is semiprime in the second sense if and only if each its proper level set
of R is semiprime in the second sense if and only if each its proper level set  is a semiprime k-ideal of R.
is a semiprime k-ideal of R.
Proof. Proof is similar to the proof of Theorem 5.6. □
6.8. Corollary
A fuzzy set  defined in Proposition 2.8 is a semiprime fuzzy k-ideal of R in the second sense if and only if A is a semiprime k-ideal of R.
defined in Proposition 2.8 is a semiprime fuzzy k-ideal of R in the second sense if and only if A is a semiprime k-ideal of R.
In view of the Transfer Principle the second definition of semiprime fuzzy k-ideal is better. Therefore fuzzy kideals which are semiprime in the first sense should be called k-semiprime.
6.9. Proposition
A non-constant fuzzy k-ideal ![]() of a commutative hemiring R with identity is semiprime if and only if
of a commutative hemiring R with identity is semiprime if and only if 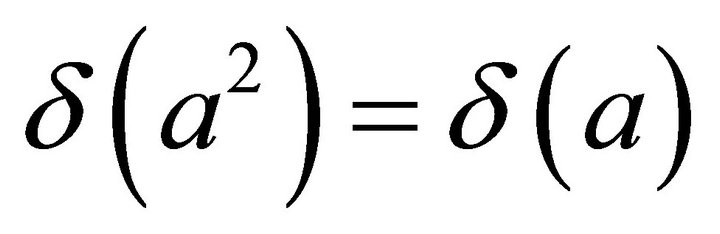 for every
for every .
.
Proof. Proof is similar to the proof of Proposition 5.8. □
Every fuzzy k-prime k-ideal is fuzzy k-semiprime kideal but the converse is not true.
6.10. Example
Consider the hemiring  defined by the following tables:
defined by the following tables:
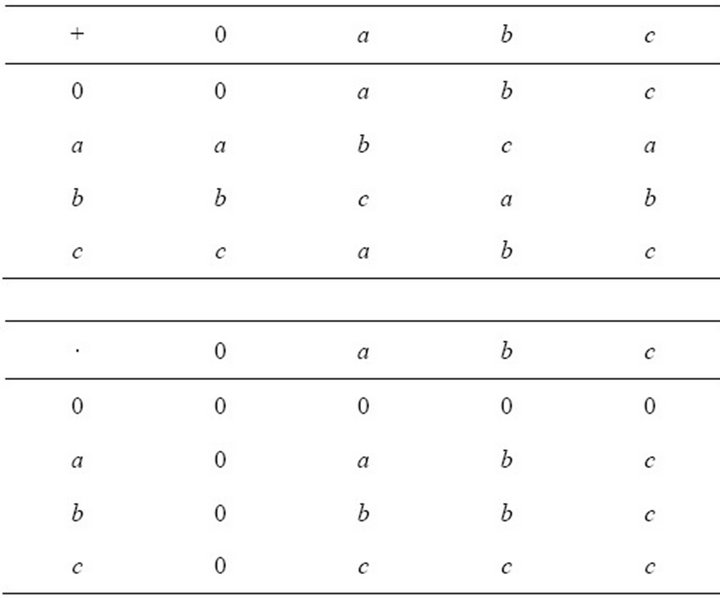
This hemiring has two k-ideals  and R. Obviously these k-ideals are idempotent.
and R. Obviously these k-ideals are idempotent.
For any fuzzy ideal ![]() of R and any
of R and any  we have
we have . Indeed,
. Indeed,
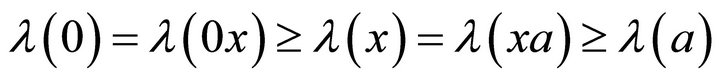 .
.
This together with
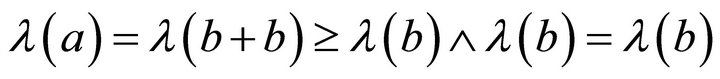
implies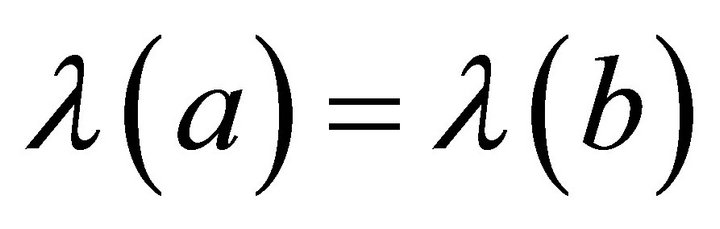 . Consequently,
. Consequently,
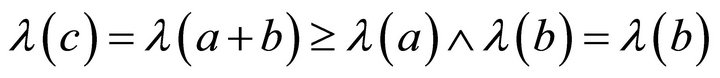 .
.
Therefore  for every fuzzy k-ideal of this hemiring.
for every fuzzy k-ideal of this hemiring.
Now we prove that each fuzzy k-ideal of R is idempotent. Since  always, so we have to show that
always, so we have to show that . Obviously, for every
. Obviously, for every  we have
we have

So, 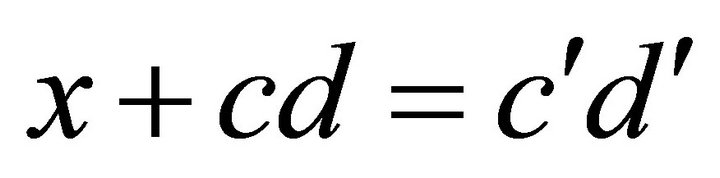 implies
implies
 .
.
Hence  implies
implies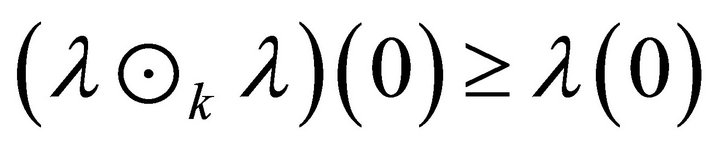 . Similarly
. Similarly 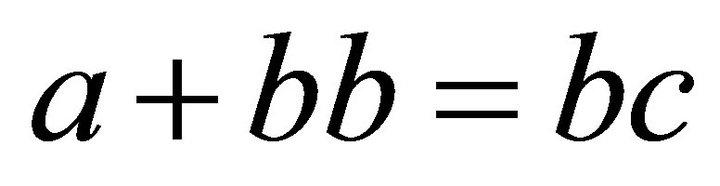 implies
implies
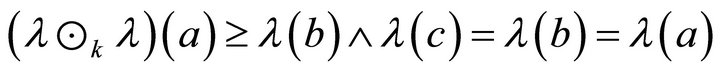 ,
,
 implies
implies
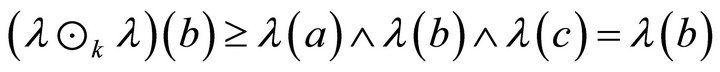 .
.
Analogously, from 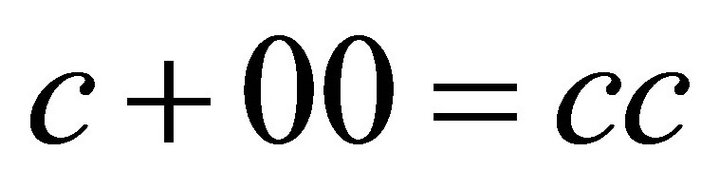 it follows
it follows
 .
.
This proves that  for every
for every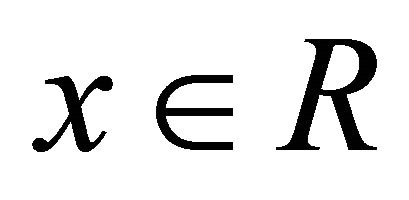 . Therefore
. Therefore 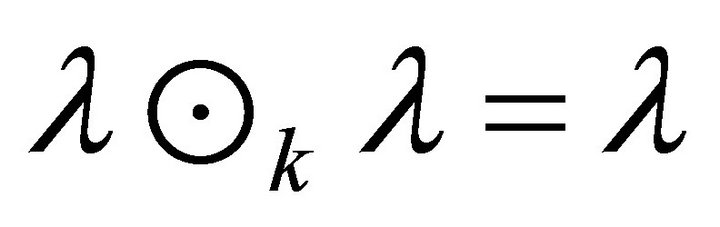 for every fuzzy k-ideal of R, which, by Theorem 6.4, means that each fuzzy k-ideal of R is semiprime.
for every fuzzy k-ideal of R, which, by Theorem 6.4, means that each fuzzy k-ideal of R is semiprime.
Consider the following three fuzzy sets:

These three fuzzy sets are idempotent fuzzy k-ideals. Since all fuzzy k-ideal of this hemiring are idempotent, by Proposition 4.1, we have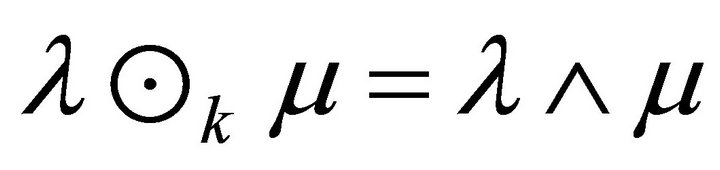 . Thus
. Thus

and

So,  but neither
but neither 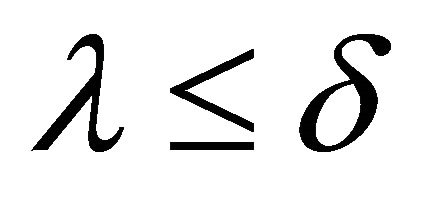 nor
nor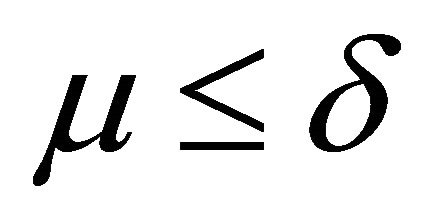 , that is
, that is ![]() is not a k-prime fuzzy k-ideal.
is not a k-prime fuzzy k-ideal.
7. Prime Spectrum
Let R be a hemiring in which each k-ideal is idempotent. Let 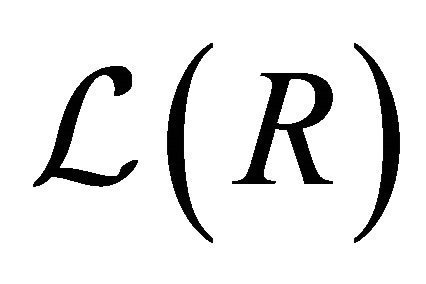 be the lattice of all k-ideals of R and
be the lattice of all k-ideals of R and 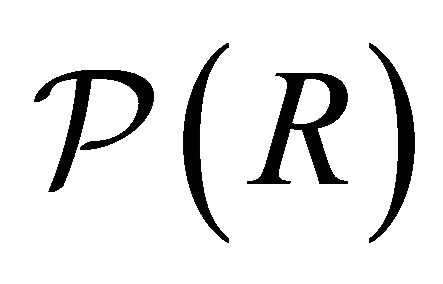 be the set of all proper prime k-ideals of R. For each k-ideal I of R define
be the set of all proper prime k-ideals of R. For each k-ideal I of R define  and
and 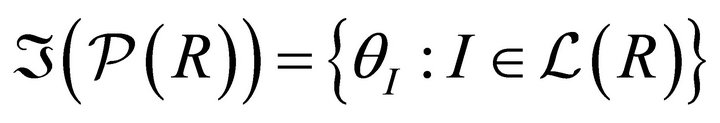 .
.
7.1. Theorem
The set 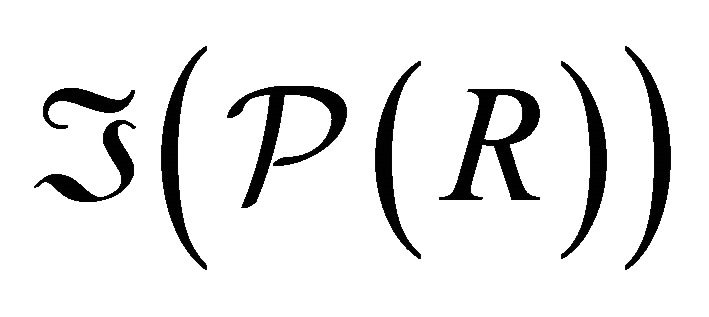 forms a topology on the set
forms a topology on the set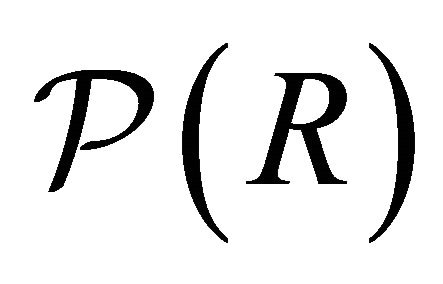 .
.
Proof. Since![]() , where
, where  is the usual empty set, because 0 belongs to each k-ideal. So empty set belongs to
is the usual empty set, because 0 belongs to each k-ideal. So empty set belongs to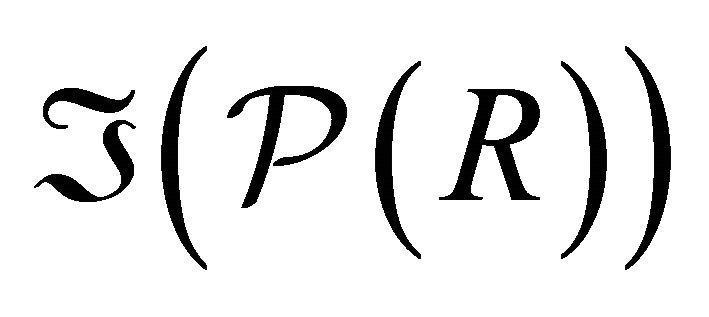 .
.
Also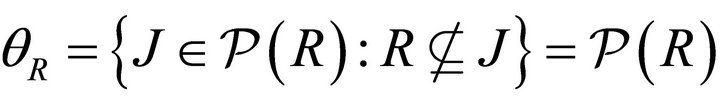 , because
, because  is the set of all proper prime k-ideals of R. Thus
is the set of all proper prime k-ideals of R. Thus 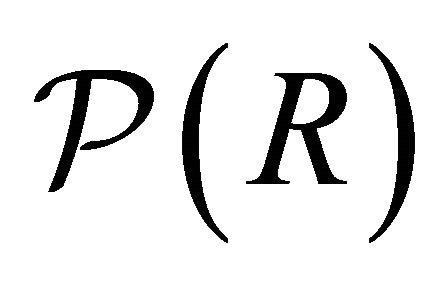 belongs to
belongs to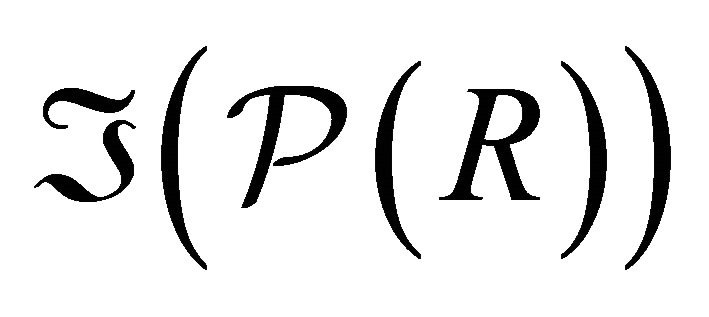 .
.
Suppose  where I1 and I2 are in
where I1 and I2 are in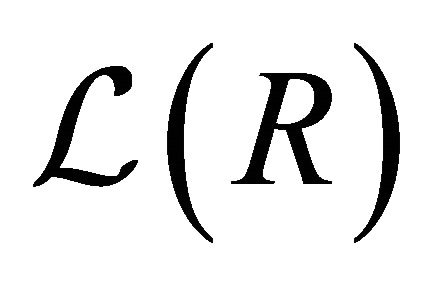 . Then
. Then
 .
.
Since each k-ideal of R is idempotent so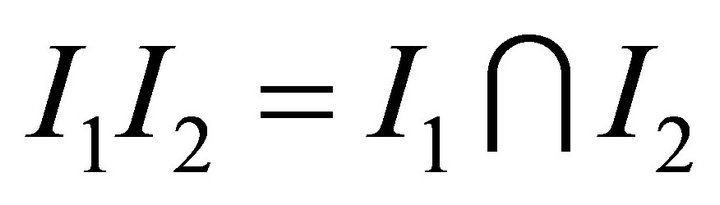 .
.
Thus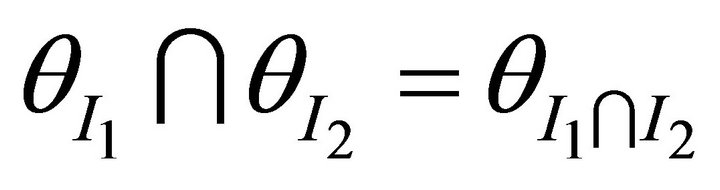 . So
. So 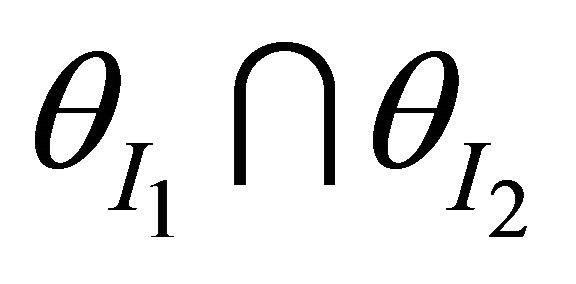 belongs to
belongs to
 .
.
Let  be an arbitrary family of members of
be an arbitrary family of members of
 . Then
. Then
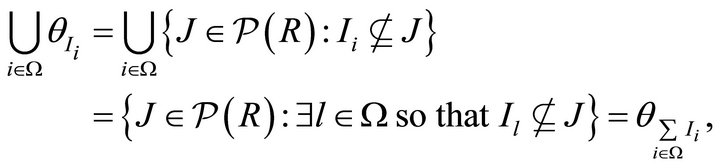
where 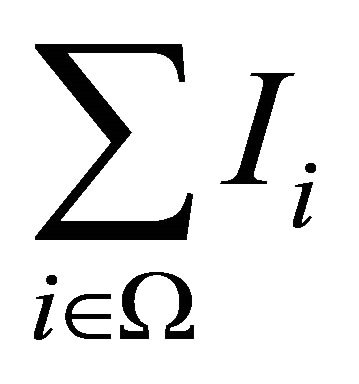 is the k-ideal generated by
is the k-ideal generated by .
.
Hence 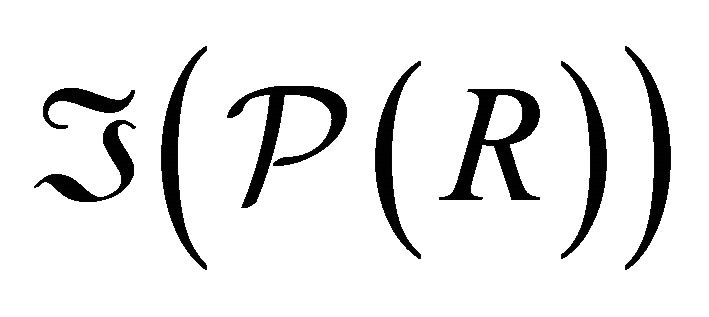 is a topology on
is a topology on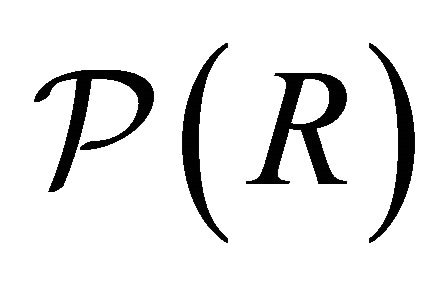 . □
. □
7.2. Definition
A fuzzy k-ideal  of a hemiring R is said to be normal if there exists
of a hemiring R is said to be normal if there exists 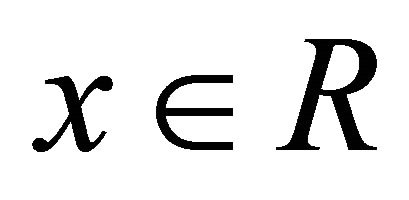 such that
such that . If
. If 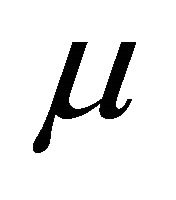 is a normal fuzzy k-ideal of R, then
is a normal fuzzy k-ideal of R, then , hence
, hence 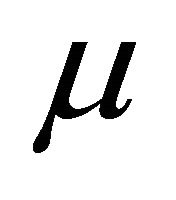 is normal if and only if
is normal if and only if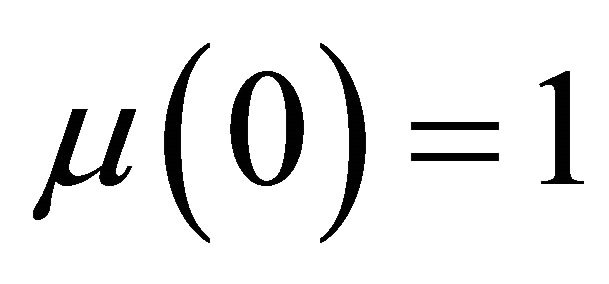 .
.
The proof of the following theorem is same as the proof of Theorem 4.4 of [29].
7.3. Theorem
A fuzzy subset ![]() of a hemiring R is a k-prime fuzzy k-ideal of
of a hemiring R is a k-prime fuzzy k-ideal of 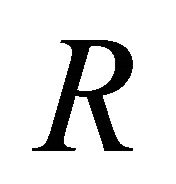 if and only if 1)
if and only if 1)  is a prime k-ideal of R.
is a prime k-ideal of R.
2) 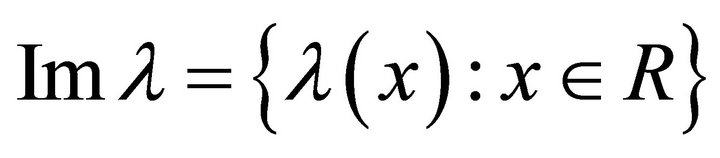 contains exactly two elements.
contains exactly two elements.
3)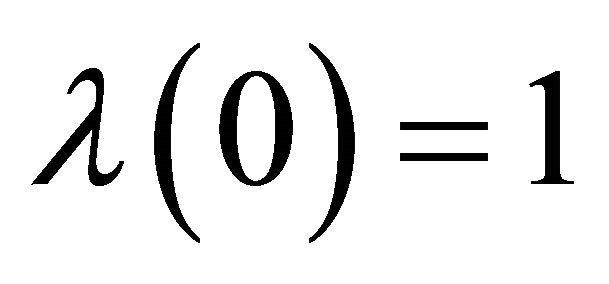 .
.
7.4. Corollary
Every k-prime fuzzy k-ideal of a hemiring is normal.
Let R be a hemiring in which each fuzzy k-ideal is idempotent, 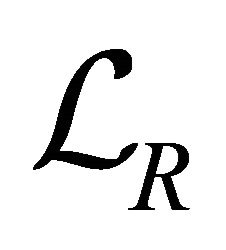 the lattice of fuzzy normal k-ideals of R and
the lattice of fuzzy normal k-ideals of R and ![]() the set of all proper fuzzy k-prime k-ideals of R. For any fuzzy normal k-ideal
the set of all proper fuzzy k-prime k-ideals of R. For any fuzzy normal k-ideal ![]() of R, we define
of R, we define 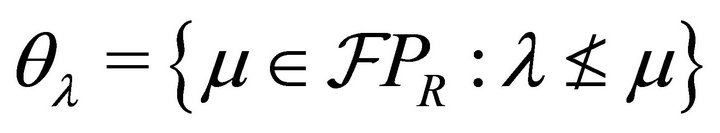 and
and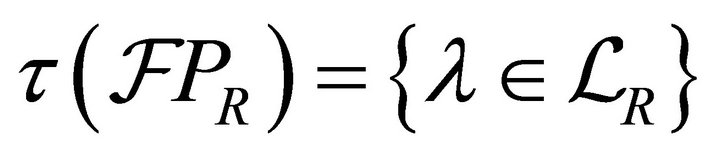 .
.
A fuzzy k-ideal ![]() of R is called proper if
of R is called proper if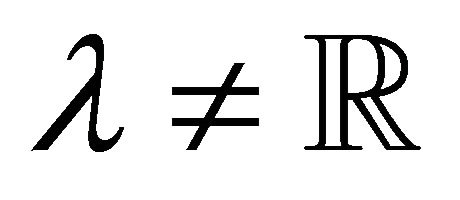 , where
, where  is the fuzzy k-ideal of R defined by
is the fuzzy k-ideal of R defined by ,
, .
.
7.5. Theorem
The set  forms a topology on the set
forms a topology on the set![]() .
.
Proof. 1) 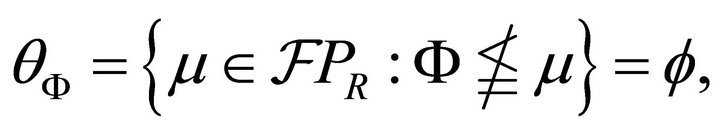 where
where  is the usual empty set and
is the usual empty set and  is the characteristic function of k-ideal
is the characteristic function of k-ideal . This follows since each k-prime fuzzy k-ideal of R is normal. Thus the empty subset belongs to
. This follows since each k-prime fuzzy k-ideal of R is normal. Thus the empty subset belongs to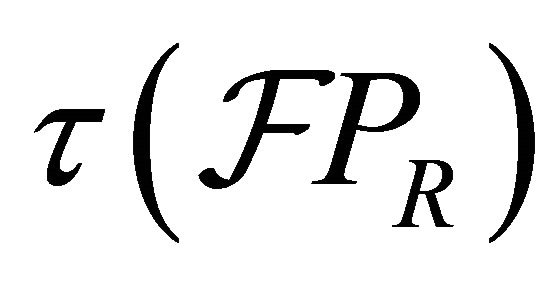 .
.
2)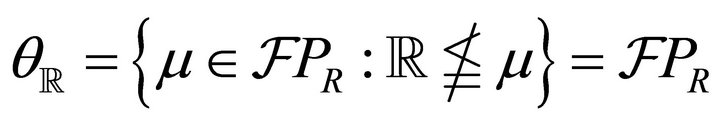 . This is true, since
. This is true, since ![]() is the set of proper k-prime fuzzy k-ideals of R. So
is the set of proper k-prime fuzzy k-ideals of R. So  is an element of
is an element of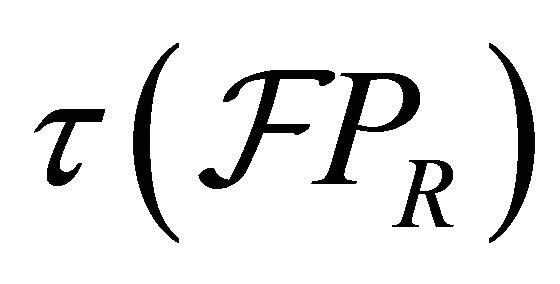 .
.
3) Let 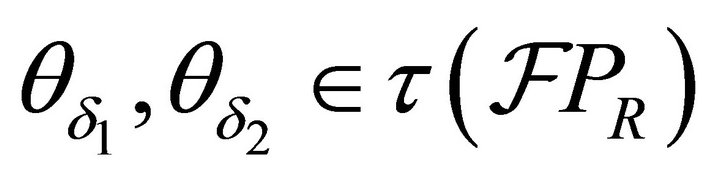 with
with .
.
Then . Since each fuzzy k-ideal of R is idempotent, this implies
. Since each fuzzy k-ideal of R is idempotent, this implies  . Thus
. Thus
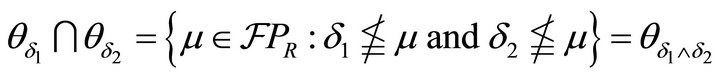 .
.
4) Let us consider an arbitrary family  of fuzzy k-ideals of R. Since
of fuzzy k-ideals of R. Since

Note that
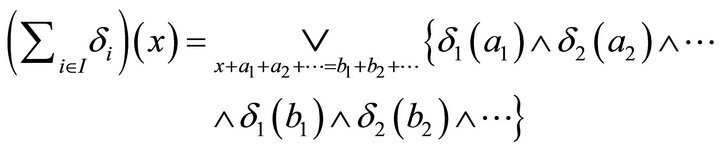
where 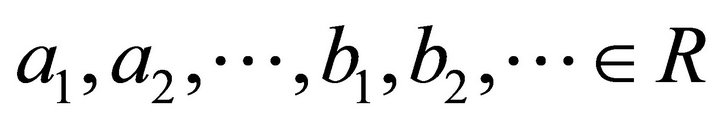 and only a finite number of the
and only a finite number of the 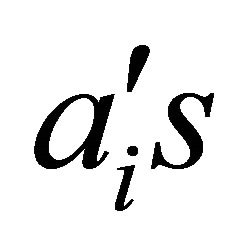 and
and  are not zero. Since
are not zero. Since  therefore we are considering the infimum of a finite number of terms because
therefore we are considering the infimum of a finite number of terms because  are effectively not being considered. Now, if for some
are effectively not being considered. Now, if for some 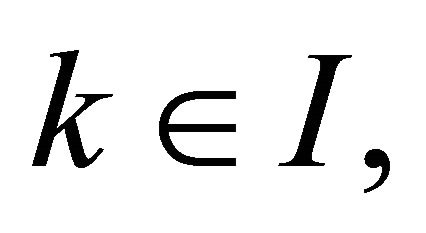
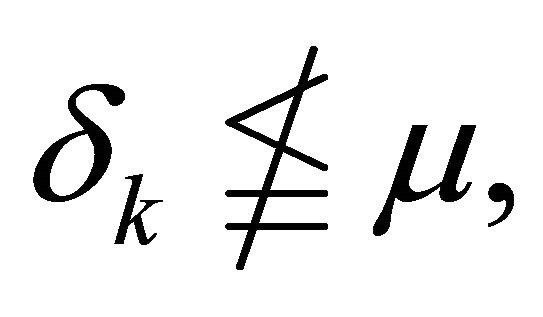 then there exists
then there exists  such that
such that . Consider the particular expression for
. Consider the particular expression for 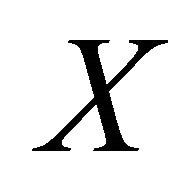 in which
in which 
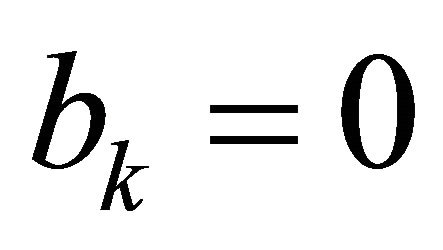 and
and 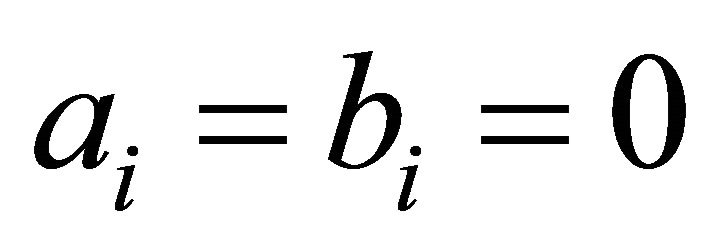 for all
for all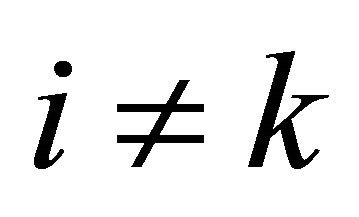 . We see that
. We see that  is an element of the set whose supremum is defined to be
is an element of the set whose supremum is defined to be
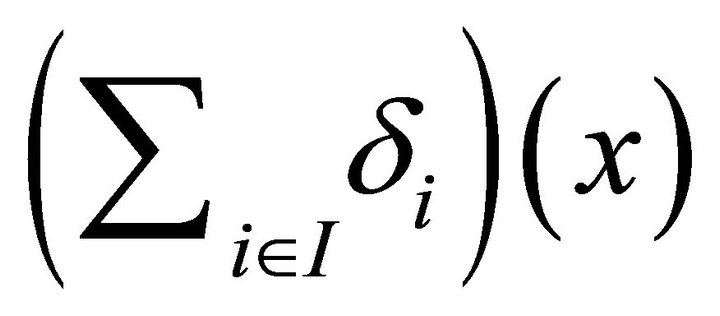 .
.
Thus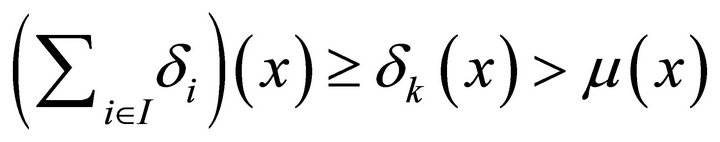 . This implies
. This implies  that is
that is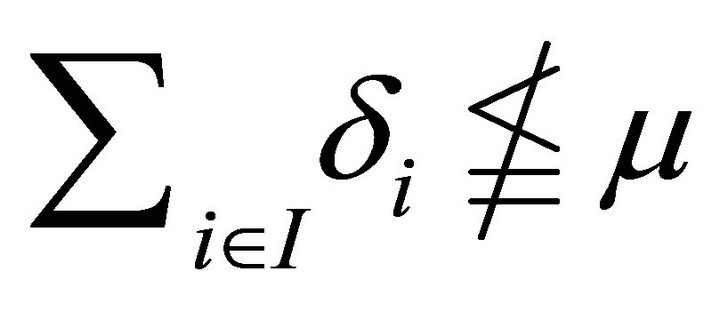 .
.
Hence 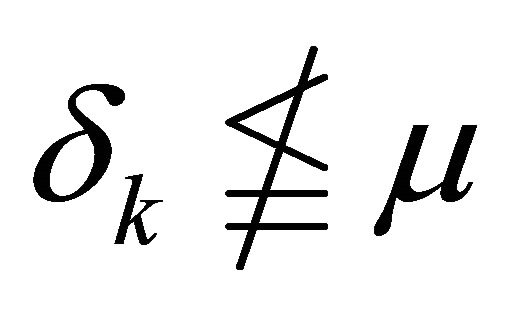 for some
for some 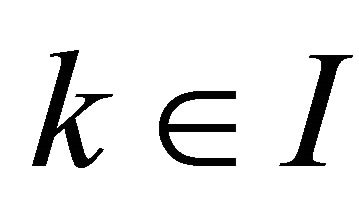 implies
implies .
.
Conversely, suppose that 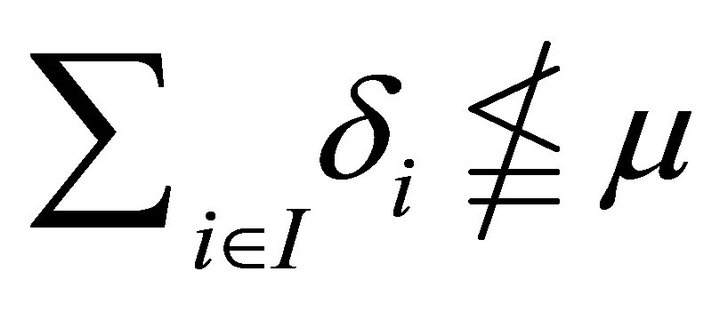 then there exists an element
then there exists an element  such that
such that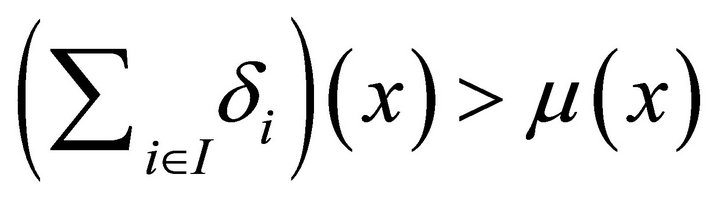 .
.
This means that

Now, if all the elements of the set (whose supremum we are taking) are individually less than are equal to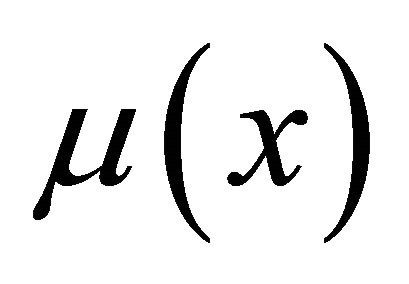 , then we have
, then we have

which does not agree with what we have assumed. Thus, there is at least one element of the set (whose supremum we are taking), say,
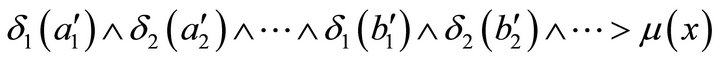 .
.
(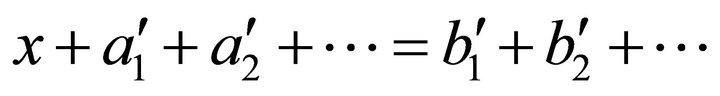 being the corresponding breakup of x, where only a finite number of
being the corresponding breakup of x, where only a finite number of  and
and 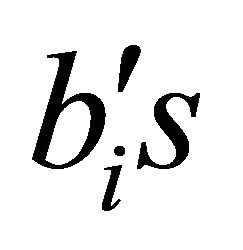 are not zero).
are not zero).
Thus,

Let
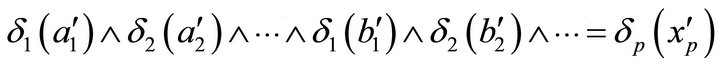
and

where .
.
So, 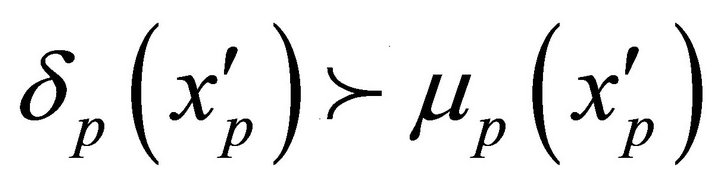 it follows that
it follows that  for some
for some .
.
Hence  implies that
implies that 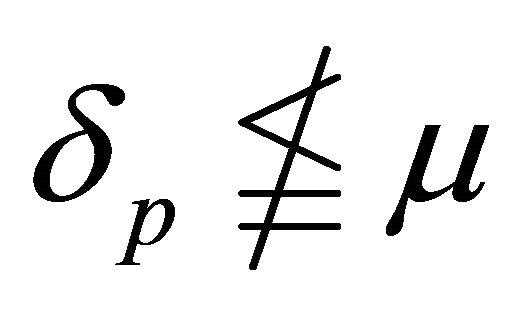 for some
for some
 .
.
Hence the two statements 1) 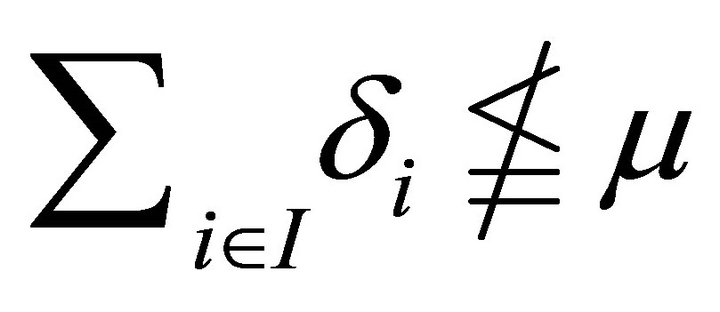 and 2)
and 2)
 for some
for some  are equivalent.
are equivalent.
Hence
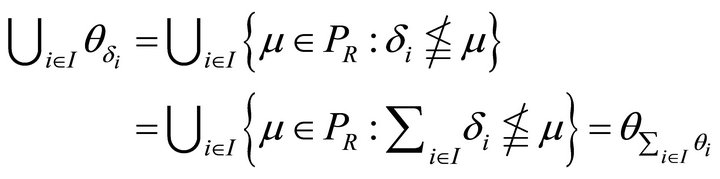
because, ![]() is also a fuzzy k-ideal of R.
is also a fuzzy k-ideal of R.
Thus, . Hence it follows that
. Hence it follows that 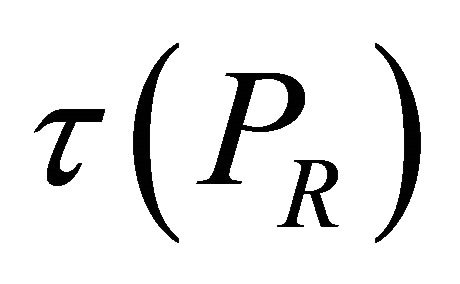 forms a topology on the set
forms a topology on the set . □
. □
8. Conclusion
In the study of fuzzy algebraic system, the fuzzy ideals with special properties always play an important role. In this paper we study those hemirings for which each fuzzy k-ideal is idempotent. We characterize these hemirings in terms of prime and semiprime fuzzy k-ideals. In the future we want to study those hemirings for which each fuzzy one sided k-ideal is idempotent and also those hemirings for which each fuzzy k-bi-ideal is idempotent.
REFERENCES
- H. S. Vandiver, “Note on a Simple Type of Algebra in Which Cancellation Law of Addition Does Not Hold,” Bulletin of the American Mathematical Society, Vol. 40, No. 12, 1934, pp. 914-920. doi:10.1090/S0002-9904-1934-06003-8
- A. W. Aho and J. D. Ullman, “Introduction to Automata Theory, Languages and Computation,” Addison Wesley, Reading, 1976.
- D. B. Benson, “Bialgebras: Some Foundations for Distributed and Concurrent Computation,” Fundamenta Informatica, Vol. 12, 1989, pp. 427-486.
- J. H. Conway, “Regular Algebra and Finite Machines,” Chapman and Hall, London, 1971.
- K. Glazek, “A Guide to Literature on Semirings and Their Applications in Mathematics and Information Sciences with Complete Bibliography,” Kluwer Academic Publishers, Berlin, 2002.
- J. S. Golan, “Semirings and Their Applications,” Kluwer Academic Publishers, Berlin, 1999. doi:10.1007/978-94-015-9333-5
- U. Hebisch and H. J. Weinert, “Semirings: Algebraic Theory and Applications in the Computer Science,” World Scientific, Singapore, 1998. doi:10.1142/3903
- W. Kuich and A. Salomma, “Semirings, Automata, Languages,” Springer Verlag, Berlin, 1986. doi:10.1007/978-3-642-69959-7
- S. Eilenberg, “Automata, Languages and Machines,” Academic Press, New York, 1974.
- E. T. Lee and L. A. Zadeh, “Note on Fuzzy Languages,” Information Sciences, Vol. 1, No. 4, 1969, pp. 421-434. doi:10.1016/0020-0255(69)90025-5
- M. Henriksen, “Ideals in Semirings with Commutative Addition,” Notices of the American Mathematical Society, Vol. 6, 1958, p. 321.
- K. Iizuka, “On the Jacobson Radial of a Semiring,” Tohoku Mathematical Journal, Vol. 11, 1959, pp. 409-421.
- D. R. LaTorre, “On h-Ideals and k-Ideals in Hemirings,” Publicationes Mathematicae (Debrecen), Vol. 12, 1965, pp. 219-226.
- L. A. Zadeh, “Fuzzy Sets,” Infection Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- J. Ahsan, K. Saifullah and M. Farid Khan, “Fuzzy Semirings,” Fuzzy Sets Systems, Vol. 60, No. 3, 1993, pp. 309- 320. doi:10.1016/0165-0114(93)90441-J
- J. Ahsan, “Semirings Characterized by Their Fuzzy Ideals,” Journal of Fuzzy Mathematics, Vol. 6, 1998, pp. 181-192.
- M. Akram and W. A. Dudek, “Intuitionistic Fuzzy Left k-Ideals of Semirings,” Soft Computing, Vol. 12, No. 9, 2008, pp. 881-890. doi:10.1007/s00500-007-0256-x
- S. I. Baik and H. S. Kim, “On Fuzzy k-Ideals in Semirings,” Kangweon Kyungki Mathematical Journal, Vol. 8, No. 2, 2000, pp. 147-154.
- T. K. Dutta and B. K. Biswan, “Fuzzy k-Ideals of Semirings,” Bulletin of Calcutta Mathematical Society, Vol. 87, 1995, pp. 91-96.
- S. Ghosh, “Fuzzy k-Ideals of Semirings,” Fuzzy Sets Systems, Vol. 95, No. 1, 1998, pp. 103-108. doi:10.1016/S0165-0114(96)00306-5
- C. B. Kim and M. Park, “k-Fuzzy Ideals in Semirings,” Fuzzy Sets Systems, Vol. 81, No. 2, 1996, pp. 281-286. doi:10.1016/0165-0114(95)00161-1
- J. Zhan and Z. Tan, “T-fuzzy k-Ideals of Semirings,” Scientiae Mathematicae Japonica, Vol. 58, 2003, pp. 597- 601.
- W. A. Dudek, M. Shabir and R. Anjum, “Characterizations of Hemirings by Their h-Ideals,” Computers & Mathematics with Applications, Vol. 59, No. 9, 2010, pp. 3167-3179. doi:10.1016/j.camwa.2010.03.003
- X. Ma and J. Zhan, “On Fuzzy h-Ideals of Hemirings,” Journal of Systems Science and Complexity, Vol. 20, No. 3, 2007, pp. 470-478. doi:10.1007/s11424-007-9043-0
- X. Ma and J. Zhan, “Generalized Fuzzy h-Bi-Ideals and h-Quasi-Ideals of Hemirings,” Information Sciences, Vol. 179, No. 9, 2009, pp. 1249-1268. doi:10.1016/j.ins.2008.12.014
- Y. Yin, X. Huang, D. Xu and F. Li, “The Characterization of h-Semisimple Hemirings,” International Journal of Fuzzy Systems, Vol. 11, No. 2, 2009, pp. 116-122.
- Y. Yin and H. Li, “The Characterizations of h-Hemiregular Hemirings and h-Intra-Hemiregular Hemirings,” Information Sciences, Vol. 178, No. 17, 2008, pp. 3451- 3464. doi:10.1016/j.ins.2008.04.002
- J. Zhan, “On Properties of Fuzzy Left h-Ideals in Hemirings with t-Norms,” International Journal of Mathematics and Mathematical Sciences, No. 19, 2005, pp. 3127-3144. doi:10.1155/IJMMS.2005.3127
- J. Zhan and W. A. Dudek, “Fuzzy h-Ideals of Hemirings,” Information Sciences, Vol. 177, No. 3, 2007, pp. 876-886. doi:10.1016/j.ins.2006.04.005
- M. K. Sen and P. Mukhopadhyay, “von Neumann Regularity in Semirings,” Kyungpook Mathematical Journal, Vol. 35, 1995, pp. 249-258.
- G. Birkhoff, “Lattice Theory,” American Mathematical Society, Providence, 1954.

