Applied Mathematics
Vol.5 No.13(2014), Article ID:47597,8 pages
DOI:10.4236/am.2014.513180
Empirical Determination of the Tolerable Sample Size for Ols Estimator in the Presence of Multicollinearity (ρ)
O. O. Alabi1, T. O. Olatayo2, F. R. Afolabi3
1Department of Mathematical Sciences, Federal University of Technology, Akure, Ondo State, Nigeria
2Department of Mathematical Sciences, Olabisi Onabanjo University, Ago-Iwoye, Ogun State, Nigeria
3Department of Mathematics and Statistics, Bowen University, Bowen, Iwo Osun State, Nigeria
Email: otimtoy@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 April 2014; revised 19 May 2014; accepted 2 June 2014
ABSTRACT
This paper investigates the tolerable sample size needed for Ordinary Least Square (OLS) Estimator to be used when there is presence of Multicollinearity among the exogenous variables of a linear regression model. A regression model with constant term (β0) and two independent variables (with β1 and β2 as their respective regression coefficients) that exhibit multicollinearity was considered. A Monte Carlo study of 1000 trials was conducted at eight levels of multicollinearity (0, 0.25, 0.5, 0.7, 0.75, 0.8, 0.9 and 0.99) and sample sizes (10, 20, 40, 80, 100, 150, 250 and 500). At each specification, the true regression coefficients were set at unity while 1.5, 2.0 and 2.5 were taken as the hypothesized value. The power value rate was obtained at every multicollinearity level for the aforementioned sample sizes. Therefore, whether the hypothesized values highly depart from the true values or not once the multicollinearity level is very high (i.e. 0.99), the sample size needed to work with in order to have an error free estimation or the inference result must be greater than five hundred.
Keywords:Regression Model, OLS Estimator Multicollinearity, Power Rate Value and Tolerable Sample Size

1. Introduction
There has been a serious argument between the researchers that multicollinearity problem could be solved with the increase of the sample size while some researchers say that Multicollinearity problem will also increase with the increase in the size of the sample. [1] stated that Multicollinearity problem could be solved by increase of the size of the sample if the presence of multicollinearity is due to errors of measurement as well as when intercorrelation happens to exist only in our original sample but not in the population [2] . Because of these arguments this paper then investigates the tolerable sample size needed for Ordinary Least Square Estimator to be used when there is presence of Multicollinearity among the exogenous variables of a linear regression model before we can say that multicollinearity problem could be solved with increase of the sample size method.
Regression theory postulates that there exists a stochastic relationship between
a variable
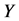 and a set of other variables
and a set of other variables . In other words,
. In other words,
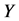 (called the dependent, endogenous or explained variable)
depends on other observed variables,
(called the dependent, endogenous or explained variable)
depends on other observed variables,
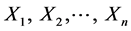 (called independent, exogenous or explanatory variables).
However, one of the assumptions of this model is that the explanatory variables
are independent. This is not often the case in economic variables. Variables like
age and year of experience do exhibit a form of linear relationship. When this assumption
is violated, it results into multicollinearity problem
[3] .
(called independent, exogenous or explanatory variables).
However, one of the assumptions of this model is that the explanatory variables
are independent. This is not often the case in economic variables. Variables like
age and year of experience do exhibit a form of linear relationship. When this assumption
is violated, it results into multicollinearity problem
[3] .
Multicollinearity could be perfect or imperfect. When it is perfect, estimates obtained are not unique [4] . If multicollinearity is not perfect, the OLS estimator has been shown to be unbiased but inefficient. Other consequences or indications of multicollinearity problem include:
1. Small changes in the data can produce significant changes in the parameter estimates (regression coefficients).
2. The regression coefficients may have wrong signs and/or unreasonable magnitudes.
3. Regression coefficients have high standard errors which result in very low values of the t-statistic and thus affect the significance of the parameters [3] [5] .
Thus, the presence of multicollinearity in a data set does not only affect parameter estimation using the OLS estimator but also inferences on the parameters of the model. Consequently, with generated collinear data, this paper attempts to investigate empirically the most tolerable sample size where power rate value of 0.99 or 1 would be obtained with ordinary least square (OLS) estimator.
2. Methodology
Consider the regression model of the form
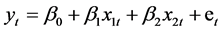 (1)
(1)
where
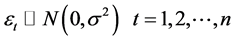
![]() is the dependent variable,
is the dependent variable,
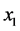 and
and
![]() are regressors which exhibit
are regressors which exhibit
![]() correlation (multicollinearity), and
correlation (multicollinearity), and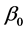 ,
,
![]() , and
, and
 are the regression coefficient (parameters) of the model.
are the regression coefficient (parameters) of the model.
Now, suppose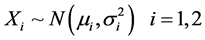 . If these variables are correlated, then
. If these variables are correlated, then
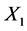 and
and
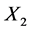 can be generated with the equations
can be generated with the equations
 (2)
(2)
where
 and
and
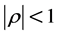 is the value of correlation between the two variables [6]
; and [7] .
is the value of correlation between the two variables [6]
; and [7] .
Monte Carlo experiments were performed 1000 times for eight sample sizes (n = 10,
20, 40, 80, 100, 150, 250 and 500) and eight levels of multicollinearity (ρ = 0,
0.25, 0.5, 0.7, 0.75, 0.8, 0.9 and 0.99) with stochastic regressors that are normally
distributed. At a particular specification of n and
 (ascenario), the first replication was obtained by generating
(ascenario), the first replication was obtained by generating . Next,
. Next,
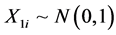 and
and
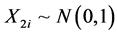 were generated using Equation (2) such that they exhibit
were generated using Equation (2) such that they exhibit
![]() correlation. The values
correlation. The values
![]() in Equation (1) were obtained by taking the true regression coefficients as unity.
This process is continued until all the 1000 replications had been done. Another
scenario is then started until all the scenarios were completed. For each replication
in the scenario, the OLS estimator of parameter estimation was used to obtain estimate
of the regression coefficients and hypothesis about the true regression coefficient
was tested at 0.05 level of significance using the t-statistic to examine the type
II error of the regression coefficients. All these were done by writing a computer
program using the Time Series Processor (TSP) software. The result of the effect
of type II error rate on OLS estimators by [8]
was considered by taken the type II error rate
in Equation (1) were obtained by taking the true regression coefficients as unity.
This process is continued until all the 1000 replications had been done. Another
scenario is then started until all the scenarios were completed. For each replication
in the scenario, the OLS estimator of parameter estimation was used to obtain estimate
of the regression coefficients and hypothesis about the true regression coefficient
was tested at 0.05 level of significance using the t-statistic to examine the type
II error of the regression coefficients. All these were done by writing a computer
program using the Time Series Processor (TSP) software. The result of the effect
of type II error rate on OLS estimators by [8]
was considered by taken the type II error rate
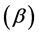 away from 1 to obtain the power rate value for every sample sizes at all levels
of multicollinearity. These power rate values were then considered at all levels
of multicollinearity for all the selected sample sizes. Then the sample size with
the power rate value of 0.999 or 1.0 was chosen as the most tolerable sample size
at each level of multicollinearity and different parameter values, [9] on effects of multicollinearity on the power rates of
the Ordinary least Squares Estimators.
away from 1 to obtain the power rate value for every sample sizes at all levels
of multicollinearity. These power rate values were then considered at all levels
of multicollinearity for all the selected sample sizes. Then the sample size with
the power rate value of 0.999 or 1.0 was chosen as the most tolerable sample size
at each level of multicollinearity and different parameter values, [9] on effects of multicollinearity on the power rates of
the Ordinary least Squares Estimators.
3. Results and Discussion
The summary of the most tolerable sample sizes at different level of multicollinearity
and different possible combination of the parameter values are shown for ,
,
![]() and
and
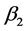 in Tables 1-8.
in Tables 1-8.
When the true values of
![]() and
and
 are maintained and that of
are maintained and that of
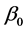 is allowed to change, The summary of the tolerable sample sizes required for the
parameter
is allowed to change, The summary of the tolerable sample sizes required for the
parameter
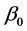 to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table1
to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table1
Table 1. The tolerable
sample sizes for
![]() when the true values of
when the true values of
![]() and
and
![]() are maintained and that of
are maintained and that of
![]() are changing at different levels of multicollinearity.
are changing at different levels of multicollinearity.
Table 2. The tolerable sample sizes for
![]() when the true values of
when the true values of
![]() and
and
![]() are maintained and that of
are maintained and that of
![]() is allowed to change at different levels of multicollinearity.
is allowed to change at different levels of multicollinearity.
Table 3. The tolerable sample sizes for
![]() when the true values of
when the true values of
![]() and
and
![]() are maintained and that of
are maintained and that of
![]() is allowed to change, at different levels of multicollinearity.
is allowed to change, at different levels of multicollinearity.
Table 4. The tolerable sample sizes for
![]() when the true value for
when the true value for
![]() is maintained and that of
is maintained and that of
![]() and
and
![]() are allowed to change at different levels of multicollinearity.
are allowed to change at different levels of multicollinearity.
Table 5. The tolerable sample sizes for
![]() when true value of is maintained and that of
when true value of is maintained and that of
![]() and
and
![]() are allow to change at different levels of multicollinearity.
are allow to change at different levels of multicollinearity.
Table 6. The tolerable sample sizes for
![]() when all the values for
when all the values for![]() ,
,
![]() and
and
![]() are allowed to change at different levels of multicollinearity.
are allowed to change at different levels of multicollinearity.
Table 7. The tolerable sample sizes for
![]() when all the values for
when all the values for![]() ,
,
![]() and
and
![]() are allowed to change at different levels of multicollinearity.
are allowed to change at different levels of multicollinearity.
Table 8. The tolerable
sample sizes for
![]() when all the values for
when all the values for![]() ,
,
![]() and
and
![]() are allowed to change at different levels of multicollinearity.
are allowed to change at different levels of multicollinearity.
Likewise, when the true values of
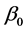 and
and
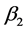 are maintained and that of
are maintained and that of
![]() is allowed to change, The summary of the tolerable sample sizes required for the
parameter
is allowed to change, The summary of the tolerable sample sizes required for the
parameter
![]() to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table2
to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table2
When the true values of
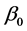 and
and
![]() are maintained and that of
are maintained and that of
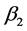 is allowed to change, The summary of the tolerable sample sizes required for the
parameter
is allowed to change, The summary of the tolerable sample sizes required for the
parameter
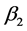 to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table3
to have a power rate value of 0.99 or 1 was determined at different levels of multicollinearity
and hypothesized values. The results for these are shown in
Table3
The summary of the tolerable sample sizes at different levels of multicollinearity and hypothesized values are shown in Table3
Also, for all other possible combinations of the parameter values similar results were obtained.
From Table 1 to Table 8 the tolerable sample size value decreases as the hypothesized values departed from the true values in all lower levels of multicollinearity, whereas at higher levels of multicollinearity the required Tolerable sample sizes increases as the hypothesized values departed from the true value. But at very high level of multicollinearity (0.99) the Tolerable sample size needed must be greater than 500 before a result with.
4. Conclusion
In conclusion, at every multicollinearity level the most tolerable sample size was then obtained as the one with the highest value of power rate, which we were able to obtain at a sample size equal or greater than five hundred. This study has revealed that whether the hypothesized values highly depart from the true values or not once the multicollinearity level is very high (i.e. 0.99), and the sample size needed to work with in order to have an error free estimation or inference result must be greater than five hundred, if and only if, increments of the size of the sample method would be used as a measure of correction to the presence of multicollinearity.
References
- Stone, R. (1961) The Measurements of Consumer Expenditure and Behavior in United Kingdom. Cambridge Publishing Company.
- Koutsoyiannis, A. (2003) Theory of Econometrics. 2nd Edition, Palgrave.
- Charterjee, S., Hadi, A.S. and Price, B. (2000) Regression Analysis by Example. 3rd Edition, Wiley-Interscience Publication, John Wiley and Sons.
- Searle, S.R. (1971) Linear Models. John Willey and Sons, New York.
- Fomby, T.B., Hill, R.C. and Johnson, S.R. (1984) Advanced Econometric Methods. Springer-Verlag, New York, Berlin, Heidelberg, London, Paris, Tokyo.
- Ayinde, K. (2006) A Comparative Study of the Performances of OLS and Some GLS Estimator When Regressors Are Both Stochastic and Collinear. West African Journal of Biophysics and Biomathematics, 2, 54-67.
- Ayinde, K. and Oyejola, B.A. (2007) A Comparative Study of the Performances of OLS and Some GLS Estimator When Stochastic Regressors Are Correlated with Error Terms. Research Journal of Applied Sciences, 2, 215-220.
- Alabi, O.O. (2007) Effects of Multicolinearity on Type 1 and Type 11 Errors of Ordinary Least Squares Estimators. Unpublished M.sc. Thesis Submitted to the Department of Statistics University of Ilorin, Ilorin.
- Alabi, O.O., Ayinde, K. and Olatayo, T.O. (2008) On Effects of Multicollinearity on the Power Rates of the Ordinary Least Squares Estimators. Journal of Mathematics and Statistics, 4, 75-80. http://dx.doi.org/10.3844/jmssp.2008.75.80


