Applied Mathematics
Vol.3 No.11(2012), Article ID:24375,3 pages DOI:10.4236/am.2012.311220
The Geometrical Theory of Science
Department of Physics and Mathematics, Federal University of Technology, Owerri, Nigeria
Email: amaghnduka@yahoo.com.au
Received August 9, 2012; revised September 12, 2012; accepted September 19, 2012
Keywords: Discrete Geometry; Partition; Quantum Mechanics; Quantum Geometrodynamics; Fundamental Particles; Causality; Chaos
ABSTRACT
Classical mechanics and quantum mechanics are the two cornerstones of science. As is well known, classical mechanics, the theory that describes the macrophysical world, has grown and flowered both in experimentation and theorization. The same is not true of quantum mechanics, the theory that describes the microphysical world. While experimentation has shown giant strides, theorization has been essentially static, having not moved appreciably beyond the great achievements of the 1920s. The reason is not difficult to fathom: while theoretical progress in classical mechanics has been intellect-driven, that in quantum mechanics, on the other hand, has been machine-driven! In this paper we describe both classical and quantum systems in an absolute and a common language (geometry). Indeed, we construct the whole of science on the basis of just three numbers, namely, 1, 2, and 3.
1. Introduction
The Newton-Galileo world is 3-dimensional and Euclidean. The state of motion of a Newtonian particle is determined by the simultaneous values of the set (qi, t; pi, H) of dynamical variables (i = 1, 2, 3). The state of rest, on the other hand, is described by the set (fi, –fi, t, H), where fi and –fi represent force and antiforce on the particle [1]. We describe the state of motion and the state of rest dimensionally by 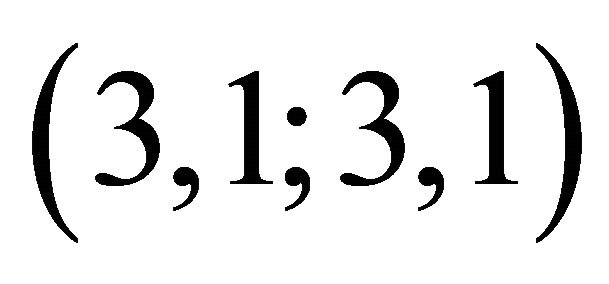 and
and 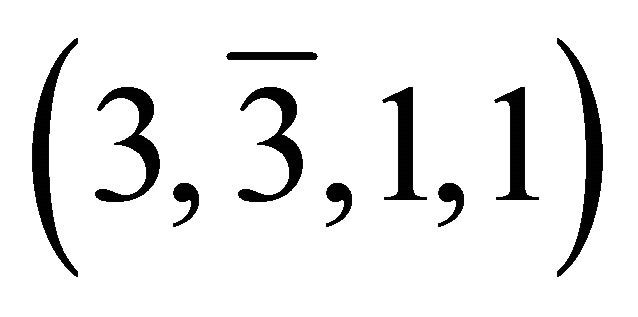 respectively, “
respectively, “ ” stands for the remotely located antiforce. Thus, in the Newton-Galileo world the state of a particle is represented by a point in an 8-dimensional space. Gravitation is also an element of this world. The particle responsible for gravitation is absolutely separated from us, hence its velocity relative to us is zero, not being an observable.
” stands for the remotely located antiforce. Thus, in the Newton-Galileo world the state of a particle is represented by a point in an 8-dimensional space. Gravitation is also an element of this world. The particle responsible for gravitation is absolutely separated from us, hence its velocity relative to us is zero, not being an observable.
Gravitation is transmitted in a definite and unchanging direction, hence it is a one-dimensional source of energy; and being remote to us we describe it dimensionally by “ ”. Clearly gravitation is a purely classical field and is adequately described by Newton’s theory of gravitation [2]. The de Broglie wavelength of the associated particle (graviton) is not defined while it has the smallest Compton wavelength. This property of the graviton must be compared with that of the photon, an elementary particle with the greatest speed and undefined Compton wavelength. The graviton is thus the heaviest elementary particle. Light (electromagnetism) was not described by Newton, except that its speed is infinite.
”. Clearly gravitation is a purely classical field and is adequately described by Newton’s theory of gravitation [2]. The de Broglie wavelength of the associated particle (graviton) is not defined while it has the smallest Compton wavelength. This property of the graviton must be compared with that of the photon, an elementary particle with the greatest speed and undefined Compton wavelength. The graviton is thus the heaviest elementary particle. Light (electromagnetism) was not described by Newton, except that its speed is infinite.
It should be noted in passing that J. C. Maxwell’s theory of electromagnetism was formulated on the basis of experimental observations; hence was written in terms of Euclidean variables, namely, Ei, Bi, t, and H [3]. Thus, the state of Maxwell’s electromagnetism may be described geometrically by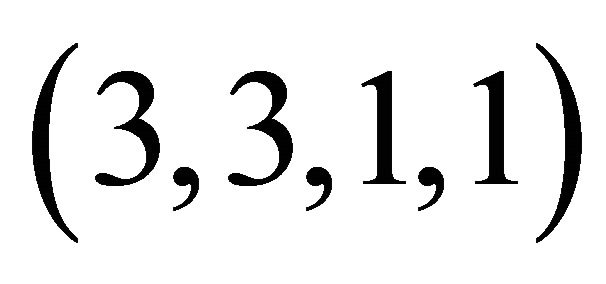 , which is Newtonian in form! This problem arises from the fact that Ei and Bi are secondary dynamical variables, and as a consequence arbitrary constraints, e.g. Coulomb gauge, Lorentz gauge, gauge invariance, etc., had to be imposed on the theory. Some have even promoted this erroneous gauge idea to a work of art, example, gauge theories of elementary particles. Economic waste is the consequence of this innocent blunder.
, which is Newtonian in form! This problem arises from the fact that Ei and Bi are secondary dynamical variables, and as a consequence arbitrary constraints, e.g. Coulomb gauge, Lorentz gauge, gauge invariance, etc., had to be imposed on the theory. Some have even promoted this erroneous gauge idea to a work of art, example, gauge theories of elementary particles. Economic waste is the consequence of this innocent blunder.
The other great space-time theory is the special theory of relativity of Albert Einstein. The Einstein-Lorentz world is 4-dimensional and Pseudo-Euclidean. The most successful application of Pseudo-Euclideanity in the classical domain is the theory of electromagnetism. Here a state is determined by the simultaneous values of the set of dynamical variables (pm, Am), m = 0, 1, 2, 3 [4]. Dimensionally the state is described by (4,4)—again a state is defined by a point in an 8-dimensional space. In this picture electromagnetic energy is transmitted at speed c along the t-axis which, in the absence of gravity, is normal to a locally flat frame of reference. Like gravitation electromagnetic energy is transmitted in onedimension, and electromagnetism, being an observable phenomenon, we represent it dimensionally by “1”. Gravitation does not feature in this picture of our world, hence the name special relativity. Einstein’s attempt to construct a theory of gravitation in a Pseudo-Euclidean environment was unsuccessful because as has been noted graviton is not a relativistic particle.
2. The Dimensionality Theorem
We recall that P.A.M. Dirac’s theory of the hydrogen atom electron is described dimensionally by (4,4) as well, where the first “4” stands for 4-momentum and the second for Dirac’s matrices [5]. It is therefore seen that these great physical theories are mere partitions of 8. This is the import of the dimensionality theorem: The states of a physical system are determined by the simultaneous values of a total of eight mutually commuting linearly independent observables. Further, we infer from these great theories that physical states are electrically neutral. The dimensionality theorem and the electrical neutrality of physical states will be used hereunder to solve the problem of matter, by matter we mean anything that possesses energy.
3. Elementary Particle Theory
In spite of the wild claims by machine-driven (model) theorists elementary particle theory has merely recorded a lot of motion but without appreciable movement since the 1920s. Indeed not much has been achieved beyond the great works of E. Schrodinger and P.A.M. Dirac. The problem has its origin in the failure of theorists to recognize that the world of the atom is manifestly discrete, hence the arsenal of differential equations, group theory, etc. are inappropriate here. We demonstrate here that geometrical approach solves the elementary particle problem with exquisite beauty.
We infer from the work of Dirac that fermions reside in 4-quantum spaces of “dimension”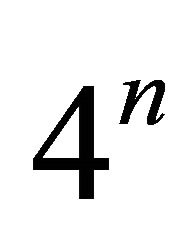 , where n is the index (called principal quantum number by physicists and period by chemists) of the space. The 4-quantum space is analogous to the 4-tensor space of tensor analysis except that it is constrained by the uncertainty principle of W. Heisenberg and exclusion principle of W. Pauli in that an N-dimensional space of tensor analysis is replaced by N-level space of quantum mechanics. The primitive (irreducible) elements of the 4-quantum spaces are the space of index
, where n is the index (called principal quantum number by physicists and period by chemists) of the space. The 4-quantum space is analogous to the 4-tensor space of tensor analysis except that it is constrained by the uncertainty principle of W. Heisenberg and exclusion principle of W. Pauli in that an N-dimensional space of tensor analysis is replaced by N-level space of quantum mechanics. The primitive (irreducible) elements of the 4-quantum spaces are the space of index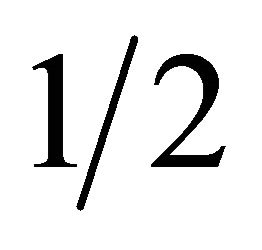 , i.e. a 2-level quantum space – n =
, i.e. a 2-level quantum space – n =  is called the rank (or spin by physicists) and a 4-quantum space of rank (spin) n = 0 which is a one-dimensional quantum space with photon as its resident. There does not exist a 4-tensor space of rank
is called the rank (or spin by physicists) and a 4-quantum space of rank (spin) n = 0 which is a one-dimensional quantum space with photon as its resident. There does not exist a 4-tensor space of rank 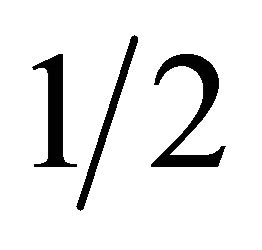 in conventional tensor analysis; hence a 4-quantum space of rank
in conventional tensor analysis; hence a 4-quantum space of rank 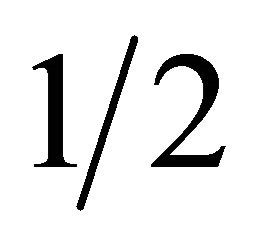 has no classical analogue. Thus, instead of 4-tensor operators as residents of 4-tensor spaces we have fermions as residents of the 4-quantum spaces of rank
has no classical analogue. Thus, instead of 4-tensor operators as residents of 4-tensor spaces we have fermions as residents of the 4-quantum spaces of rank 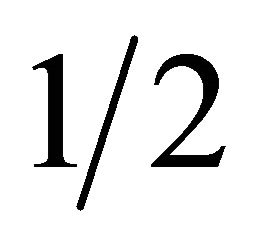 (or indeed of any index as we shall see).
(or indeed of any index as we shall see).
Reducibility Scenario
A 4-quantum space of index n ³ 1,  , is reducible. One can establish the following fundamental theorem by induction: A 4-quantum space of index n ³ 2 (
, is reducible. One can establish the following fundamental theorem by induction: A 4-quantum space of index n ³ 2 (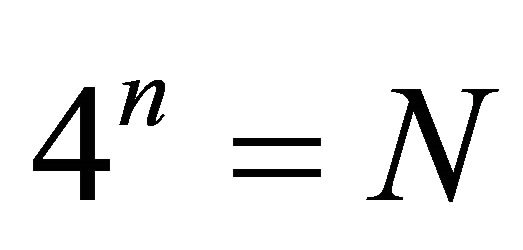 , say) is reducible according to the following fundamental formula,
, say) is reducible according to the following fundamental formula,
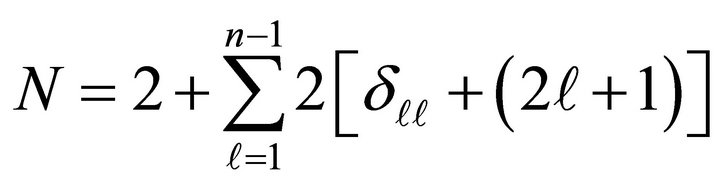 (1)
(1)
where l is orbital angular momentum. The prototype space of index n = 1 is special. The n = 1, or N = 4 = (2 + 2) (which we write in the form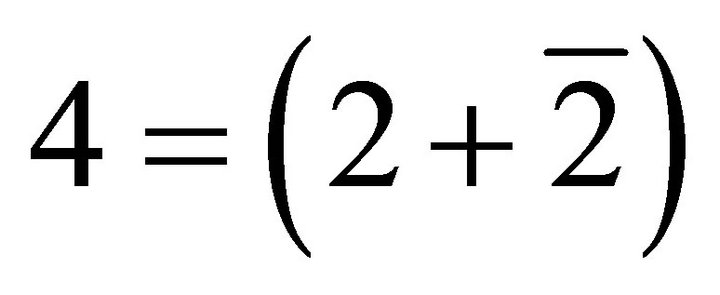 , in agreement with the Dirac theory)is a spin space which has no classical analogue. The spaces of “dimensions” 2 and
, in agreement with the Dirac theory)is a spin space which has no classical analogue. The spaces of “dimensions” 2 and  have fermions and anti-fermions respectively as the residents, and we denote this by (2,
have fermions and anti-fermions respectively as the residents, and we denote this by (2, ). The Dirac solution is, however, special in that it applies to charged fermions (electrons and protons) only. The electrical neutrality of physical states requires that we include neutral fermions (neutrinos and neutrons). Thus the geometrical structure for the case n = 1 is
). The Dirac solution is, however, special in that it applies to charged fermions (electrons and protons) only. The electrical neutrality of physical states requires that we include neutral fermions (neutrinos and neutrons). Thus the geometrical structure for the case n = 1 is 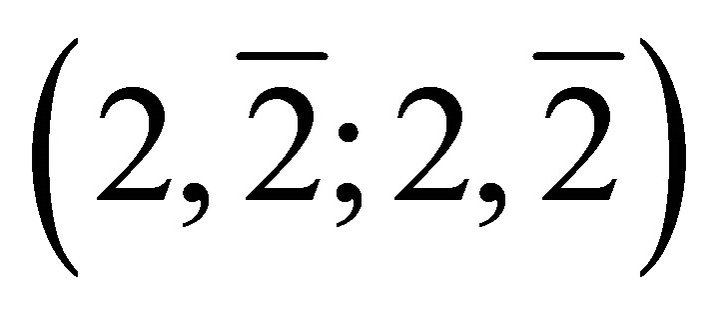 in complete agreement with the dimensionality theorem. Thus, the fermion ground state is again a partition of 8.
in complete agreement with the dimensionality theorem. Thus, the fermion ground state is again a partition of 8.
The state of index 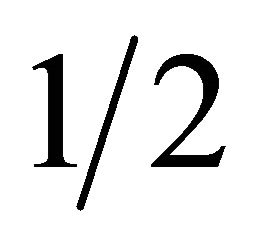 gives the He(n = 1) and antihelium
gives the He(n = 1) and antihelium 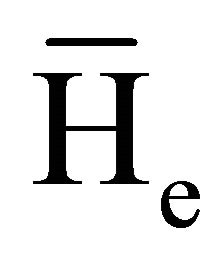 (n = 1) group; of chemical elements. The formula (1) is certainly true for atoms of the Ne (n = 2), Ar(n = 3), Kr(n = 4), Xe(n = 5), and Rn(n = 6) groups of chemical elements. Since n and l in (1) take integral values (
(n = 1) group; of chemical elements. The formula (1) is certainly true for atoms of the Ne (n = 2), Ar(n = 3), Kr(n = 4), Xe(n = 5), and Rn(n = 6) groups of chemical elements. Since n and l in (1) take integral values (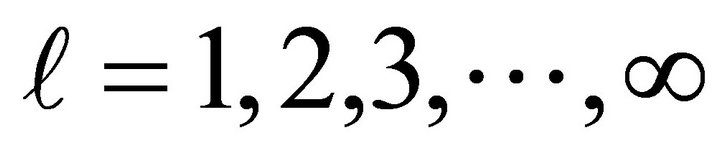 ), we have in principle an infinite number of groups of chemical elements. Thus, formula (1) gives, together with the special cases of rank
), we have in principle an infinite number of groups of chemical elements. Thus, formula (1) gives, together with the special cases of rank 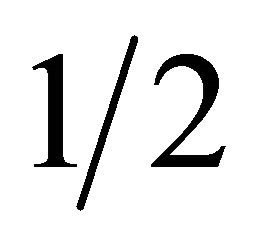 and n = 1, the theoretical derivation of the periodic table of the chemical elements; and with it explicit structures of atoms, molecules, and nuclei.
and n = 1, the theoretical derivation of the periodic table of the chemical elements; and with it explicit structures of atoms, molecules, and nuclei.
Again there exist 3-quantum spaces of index n (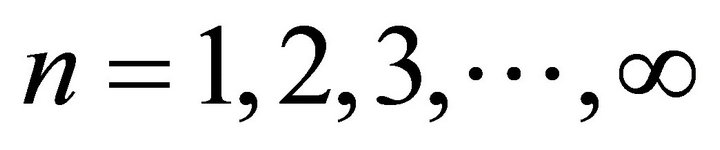 ) which are the analogues of 3-tensor spaces of tensor analysis. The primitive (irreducible) elements of the 3-quantum spaces are the 3-quantum space of rank (spin) zero and the 3-quantum space of rank (spin) one. The 3-tensor spaces of index n ³ 1 of tensor analysis do not have analogues in quantum physics. The residents of these 3-quantum spaces are bosons, namely, graviton for the space of rank (spin) zero and Ws for the space of rank (spin) one. In the conventional (standard model) particle physics theory the graviton is called the Z0 particle and is erroneously claimed to carry the weak force, and the particle of spin one is called the W (
) which are the analogues of 3-tensor spaces of tensor analysis. The primitive (irreducible) elements of the 3-quantum spaces are the 3-quantum space of rank (spin) zero and the 3-quantum space of rank (spin) one. The 3-tensor spaces of index n ³ 1 of tensor analysis do not have analogues in quantum physics. The residents of these 3-quantum spaces are bosons, namely, graviton for the space of rank (spin) zero and Ws for the space of rank (spin) one. In the conventional (standard model) particle physics theory the graviton is called the Z0 particle and is erroneously claimed to carry the weak force, and the particle of spin one is called the W (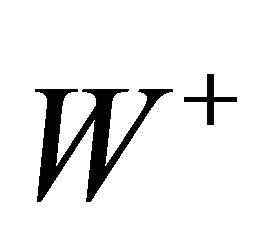 and
and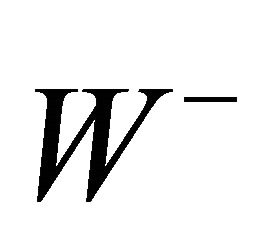 ) particle and is claimed to carry the weak force as well!
) particle and is claimed to carry the weak force as well!
The fundamental boson state, consistent with the dimensionality theorem, has the structure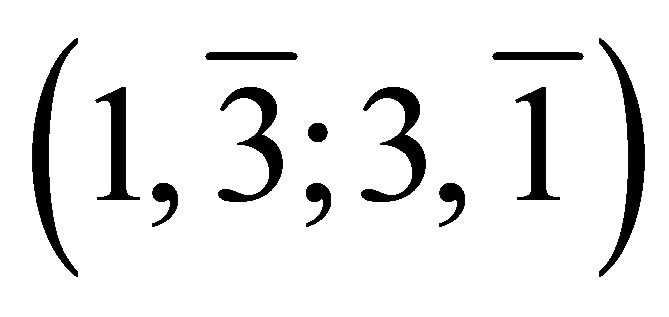 , which is yet another partition of 8. The building blocks of this state, consistent with the electrical neutrality of physical states, are
, which is yet another partition of 8. The building blocks of this state, consistent with the electrical neutrality of physical states, are  and
and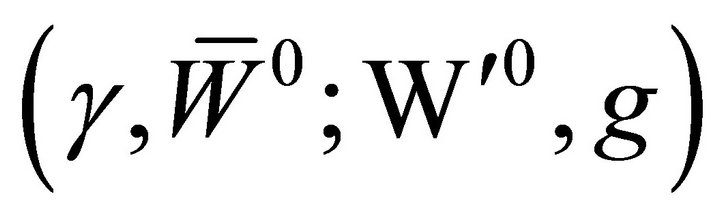 , where g and g stand for the photon and graviton respectively and the W0 (
, where g and g stand for the photon and graviton respectively and the W0 (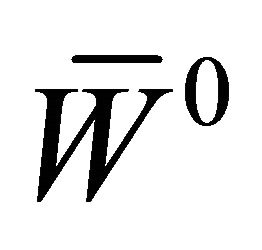 ) stand for the neutral Ws. The Ws mediate both weak and strong nuclear interaction as we shall see. We have here the unification of the four fundamental forces into a single electro-gravi-nuclear force.
) stand for the neutral Ws. The Ws mediate both weak and strong nuclear interaction as we shall see. We have here the unification of the four fundamental forces into a single electro-gravi-nuclear force.
The final partition of 8, consistent with the constraint that the geometry of the quantum space be 4-dimensional Pseudo-Euclidean space, gives the geometrical structure of the fundamental fermion-boson state as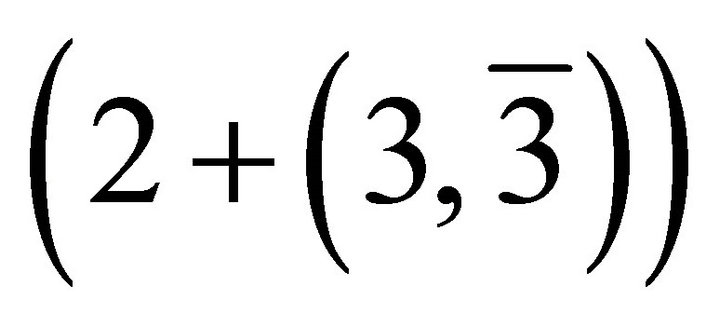 ; or
; or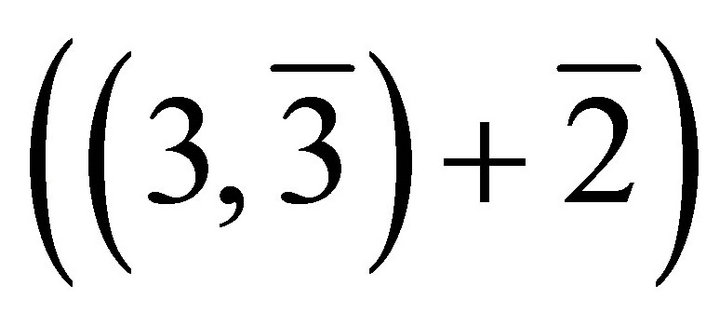 , where the “+” stands for weak nuclear interaction if neutrinos are involved and strong nuclear interaction if neutrons are involved. Contrary to conventional wisdom the proton is not involved in nuclear interaction. The implication of this, consistent with the electrical neutrality of physical states, is that there exist only three lepton states, namely, (electron, electron-neutrino), (muon, muon-neutrino), and (tauon, tauon-neutrino) corresponding to the charged nuclear states, namely, (proton, antiproton; neutron, antineutron),
, where the “+” stands for weak nuclear interaction if neutrinos are involved and strong nuclear interaction if neutrons are involved. Contrary to conventional wisdom the proton is not involved in nuclear interaction. The implication of this, consistent with the electrical neutrality of physical states, is that there exist only three lepton states, namely, (electron, electron-neutrino), (muon, muon-neutrino), and (tauon, tauon-neutrino) corresponding to the charged nuclear states, namely, (proton, antiproton; neutron, antineutron),
 , and
, and 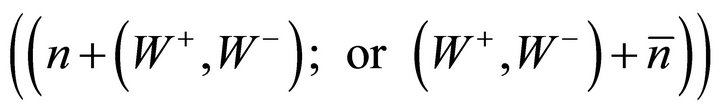 .
.
4. Conclusion
Our geometrical theory, called quantum geometro-dynamics, has enormous implications. Indeed almost all of the conventional microphysical theories are now for the trash can—it is a revolution! These issues are outside the scope of this paper; it is, however, necessary to mention a few here. Nature admits matter-antimatter symmetry; the only asymmetry in nature is geometrical (see the boson geometrical structure). Quarks and Higgs boson (or bosons) do not exist in nature. The Higgs boson idea arose from the wrong interpretation of the Z0 particle— its existence would imply a fifth fundamental interaction which is absolutely unnecessary. The graviton gives mass to the particles of nature—the mass quantum numbers relative to the graviton are rational numbers, whereas the charge quantum numbers are integral. Further, neutrino oscillation does not occur in nature, otherwise the universe would not exist. Finally, the fermion-boson world is chaotic, and accounts for weak and strong nuclear processes including fusion. Fusion is actually a 3-body process which has a geometrical origin; it has nothing in common with the erroneous Bethe fusion processes. Fusion arises from the fact that it is impossible to construct 4 × 4 matrices from a 2 × 2 and 6 × 6 matrices by mere juxtaposition.
REFERENCES
- H. Goldstein, “Classical Mechanics,” Addison-Wesley Publishing Company, Inc., Boston, 1959.
- K. R. Symon, “Mechanics,” 2nd Edition. Addison-Wesley Publishing Company, Inc., Reading, 1964.
- J. D. Jackson, “Classical Electrodynamics,” 3rd Edition, John Wiley and Sons, Ltd., Chichester, 1998.
- L. D. Landau and E. M. Lifshitz, “The Classical Theory of Fields,” 3rd Edition, Pergamon Press, Oxford, 1971.
- V. B. Berestetskii, E. M. Lifshitz and L. P. Pithaevskii, “Relativistic Quantum Theory,” Pergamon Press, Oxford, 1971.

