Applied Mathematics
Vol.3 No.9(2012), Article ID:22995,7 pages DOI:10.4236/am.2012.39144
Exponential Dichotomy and Eberlein-Weak Almost Periodic Solutions*
1Départment de Mathématiques, Faculté des Sciences Semlalia, Université Cadi Ayyad, Marrakesh, Morocco 2Laboratoire L. M. C., Départment de Mathématiques et Informatique, Faculté Polydisciplinaire-Safi (FPS) Université Cadi Ayyad, Safi, Morocco
Email: aitdads@uca.ma, s.fatajou@ucam.ac.ma, lllahcen@gmail.com
Received July 26, 2012; revised August 26, 2012; accepted September 4, 2012
Keywords: Bounded Solutions; Almost Periodic and Eberlein Weak Almost Periodic Functions; Exponential Dichotomy; Linear Differential Equations
ABSTRACT
We give sufficient conditions ensuring the existence and uniqueness of an Eberlein-weakly almost periodic solution to the following linear equation
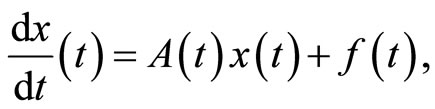
in a Banach space X, where  is a family of infinitesimal generators such that for all
is a family of infinitesimal generators such that for all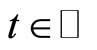 ,
, 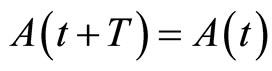 for some
for some 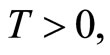 for which the homogeneuous linear equation
for which the homogeneuous linear equation 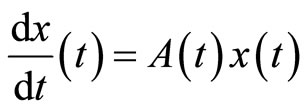 is well posed, stable and has an exponential dichotomy, and
is well posed, stable and has an exponential dichotomy, and 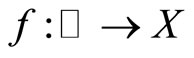 is Eberlein-weakly amost periodic.
is Eberlein-weakly amost periodic.
1. Introduction
The aim of this work is to investigate the existence and uniqueness of a weakly almost periodic solution in the sense of Eberlein for the following linear equation :
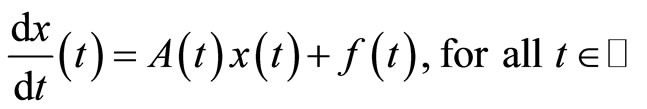 (1)
(1)
for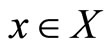 , where X is a complex Banach space,
, where X is a complex Banach space, 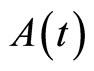 is (unbounded) linear operator acting on X for every fixed
is (unbounded) linear operator acting on X for every fixed  such that for all
such that for all ,
, 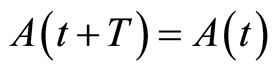 for some
for some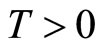 , and the input function
, and the input function 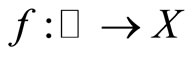 is weakly almost periodic in the sense of Eberlein (Eberlein-weakly almost periodic). In the sequel, we essentially assume that:
is weakly almost periodic in the sense of Eberlein (Eberlein-weakly almost periodic). In the sequel, we essentially assume that:

 is a family of infinitesimal generators for which the corresponding homogeneous equation of (1) is well posed and stable in the following sense: there exists a T-periodic strongly continuous evolutionary process
is a family of infinitesimal generators for which the corresponding homogeneous equation of (1) is well posed and stable in the following sense: there exists a T-periodic strongly continuous evolutionary process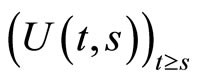 , which is uniformly bounded and strongly continuous such in particular that:
, which is uniformly bounded and strongly continuous such in particular that:
for all

and
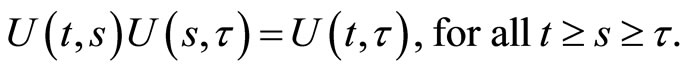
Further, if 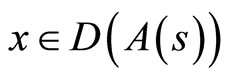 is given and
is given and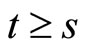 , then
, then 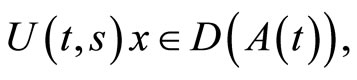 and
and

We also assume
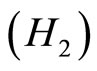 The corresponding homogeneous equation of (1) has an exponential dichotomy, i.e., there exist a family of projections
The corresponding homogeneous equation of (1) has an exponential dichotomy, i.e., there exist a family of projections 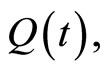
 and positive constants
and positive constants 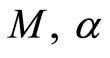 such that the following conditions are satisfied :
such that the following conditions are satisfied :
1) For every fixed 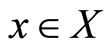 the map
the map 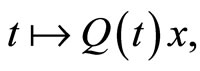 is continuous and T-periodic
is continuous and T-periodic
2) 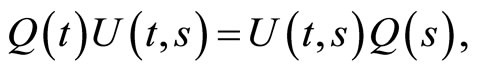
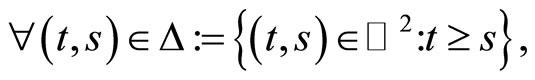
3) 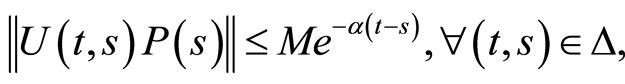 where for all
where for all  and
and 

4) 
5)  is an isomorphism from
is an isomorphism from  onto
onto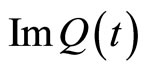 ,
, 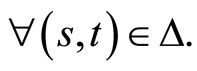
The problem of the existence of almost periodic solutions has been extensively studies in the literature [1-6]. Eberlein-weak almost periodic functions are more general than almost periodic functions and they were introduced by Eberlein [7], for more details about this topics we refer to [8-11] where the authors gave an important overview about the theory of Eberlein weak almost periodic functions and their applications to differential equations. In the literature, many works are devoted to the existence of almost periodic and pseudo almost periodic solutions for differential equations (a pseudo almost periodic function is the sum of an almost periodic function and of an ergodic perturbation), but results about Eberlein weak almost periodic solutions are rare [7,12-16].
In ([17], Chap. 3) the authors investigate the existence and uniqueness of an almost periodic solution for equation (1) when the corresponding homogeneous equation of (1) has an exponential dichotomy and the function f is almost periodic. In ([17], Chap. 3) the authors showed that, if the corresponding homogeneous equation of (1) has an exponential dichotomy and the function f is almost periodic, the equation (1) has a unique bounded integral solution on  which is also almost periodic. Here we propose to extend the result in [17] to the Eberleinweakly almost periodic case.
which is also almost periodic. Here we propose to extend the result in [17] to the Eberleinweakly almost periodic case.
2. Eberlein-Weak Almost Periodic Functions
In the sequel, we give some properties about weak almost periodic functions in the sense of Eberlein (Eberlein-weak almost periodic functions).
Let X and Y be two Banach spaces. Denote by 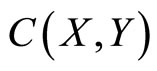 the space of all continuous functions from X to Y. Let
the space of all continuous functions from X to Y. Let 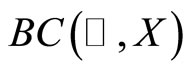 be the space of all bounded and continuous functions from
be the space of all bounded and continuous functions from  to X, equipped with the norm of uniform topology.
to X, equipped with the norm of uniform topology.
Definition 2.1 A bounded continuous function 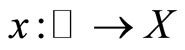 is said to be almost periodic, if the orbit of x, the set of translates of x:
is said to be almost periodic, if the orbit of x, the set of translates of x:
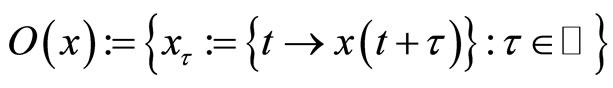
is a relatively compact set in 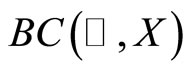 with respect to the supremum norm.
with respect to the supremum norm.
We denote these functions by
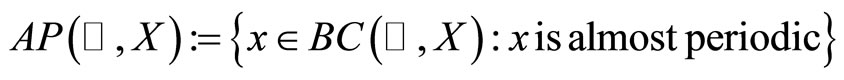
Definition 2.2 A function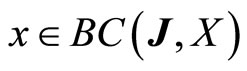 , for
, for 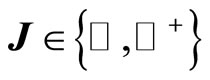 is said to be weakly almost periodic in the sense of Eberlein (Eberlein-weakly almost periodic) if the orbit of x with respect to J:
is said to be weakly almost periodic in the sense of Eberlein (Eberlein-weakly almost periodic) if the orbit of x with respect to J:
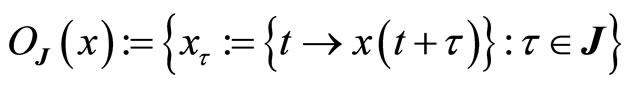
is relatively compact with respect to the weak topology of the sup-normed Banach space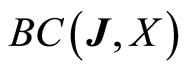 .
.
For the sequel, 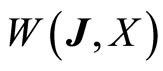 will denote the set of Eberlein-weakly almost periodic X valued functions.
will denote the set of Eberlein-weakly almost periodic X valued functions.
Theorem 2.3 Equipped with the norm
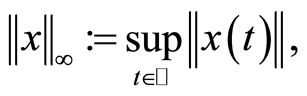
the vector space 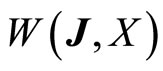 is a Banach space.
is a Banach space.
In [18,19] Deleeuw and Glicksberg proved that if we consider the subspace of those Eberlein weakly almost periodic functions, which contain zero in the weak closure of the orbit (weak topology of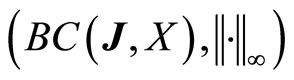 ), i.e.;
), i.e.;
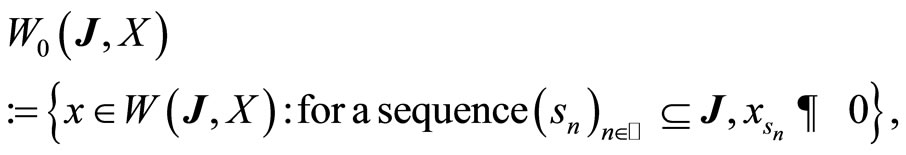
the following decomposition
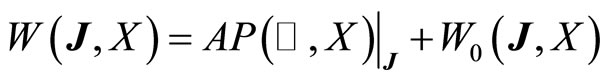
holds. Moreover, if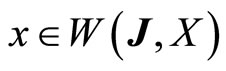 ,
, 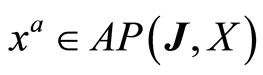 , and
, and 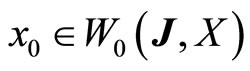 with
with 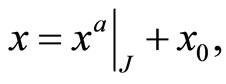 then
then
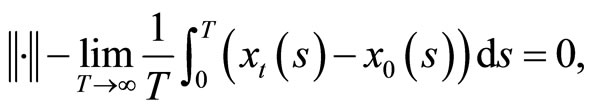
uniformly in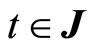 .
.
For a more detailed information about the decomposition and the ergodic result we refer to the book of Krengel [20,21].
In order to prove the weak compactness of the translates, Ruess and Summers extended the double limits criterion of Grothendieck [22] to the following:
Proposition 2.4 A subset 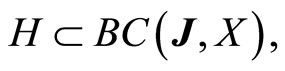 is relatively weakly compact if and only if
is relatively weakly compact if and only if
1) H is bounded in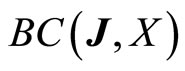 , and
, and
2) for all 
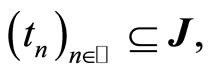 and
and 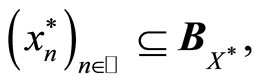 the following double limits condition holds:
the following double limits condition holds:
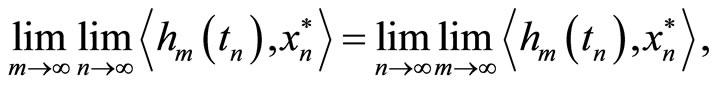
whenever the iterated limits exist.
This result will be the main tool in verifying weak almost periodicity. For the other task we will use.
Proposition 2.5 For every Eberlein weakly almost periodic function f there exists a sequence 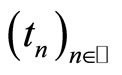 such that if g is the almost periodic part
such that if g is the almost periodic part 
3. Statement of the Main Result
In this section, we state a result of the existence and uniqueness of an Eberlein-weakly almost periodic solution of the Periodic Inhomogeneous Linear Equation (1). The existence and uniqueness of an almost periodic and bounded solution has been studied by M. N’Guérékata ([17]). More precisely, the author proved the following result.
Theorem 3.1 ([17]) Assume that 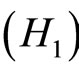 and
and 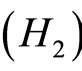 hold. If the function f is continuous and bounded on
hold. If the function f is continuous and bounded on  then Equation (1) has a unique bounded mild solution
then Equation (1) has a unique bounded mild solution 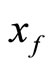 on
on  Moreover, if f is almost periodic, then
Moreover, if f is almost periodic, then 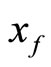 is almost periodic.
is almost periodic.
We propose to extend the above theorem to the case where f is Eberlein-weakly almost periodic.
Theorem 3.2 Assume that  and
and 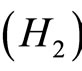 hold. If the function f is Eberlein-weakly almost periodic with a relatively compact range, then Equation (1) has a unique bounded mild solution
hold. If the function f is Eberlein-weakly almost periodic with a relatively compact range, then Equation (1) has a unique bounded mild solution 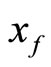 on
on  which is Eberleinweakly almost periodic.
which is Eberleinweakly almost periodic.
For the proof of theorem (3.2), we use the following lemmas.
Lemma 3.3 Let  be a bounded uniformly continuous function with relatively compact range,
be a bounded uniformly continuous function with relatively compact range, 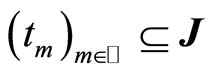 ,
, 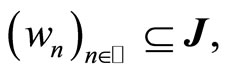 and
and  If
If  , or
, or 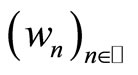 is bounded, then one has
is bounded, then one has
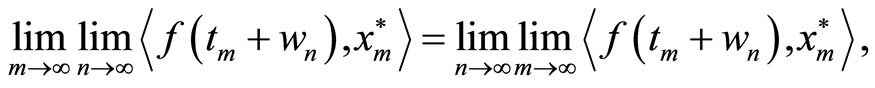
whenever the iterated limits exist.
Proof. Noting that only the equality of the iterated limits has to be proved, we may pass to subsequences. Therefore we assume that the following limits exists
1) 
2) 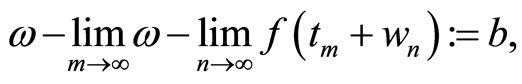
3) 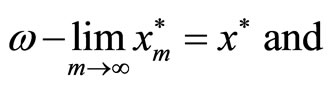
4) 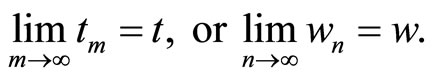
here 1) and 2) can be obtained by a diagonalization argument. Since 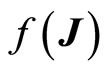 is separable, we may assume that 3) holds.
is separable, we may assume that 3) holds.
Let  then by the uniform continuity of f, we find
then by the uniform continuity of f, we find
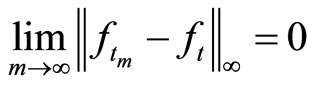
and
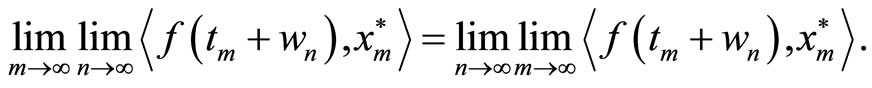
Again by uniform continuity of f, and by the choice of subsequences we find for the interchanged limits.
Lemma 3.4 Let 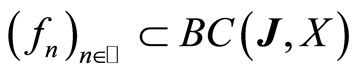 such that for a subcompact set
such that for a subcompact set
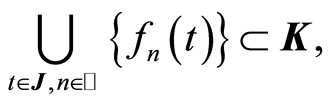
and
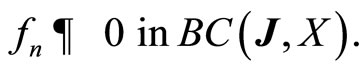
Then 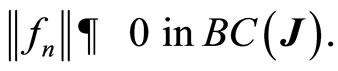
Proof. We first prove that the set 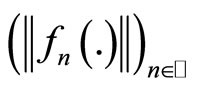 is weakly relatively compact in
is weakly relatively compact in  Thus, for given sequences
Thus, for given sequences 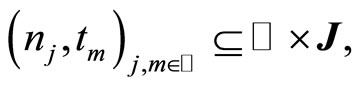 we have to verify the following identity :
we have to verify the following identity :

whenever the iterated limits exist. Since 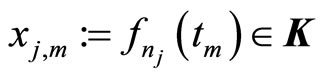 for all
for all 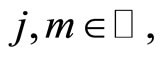 as a consequence of the metric weak compactness of K, we may pass to subsequences of
as a consequence of the metric weak compactness of K, we may pass to subsequences of  and
and 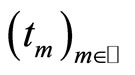 such that the iterated limits of
such that the iterated limits of 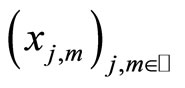 exist in X, without loss of generality the sequences are chosen in this way. The characterization of weak compactness gives,
exist in X, without loss of generality the sequences are chosen in this way. The characterization of weak compactness gives,
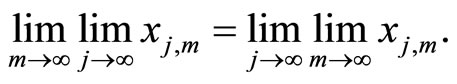
Since 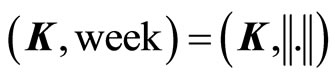 (the convergence holds in norm), hence one will obtain that
(the convergence holds in norm), hence one will obtain that  is weakly relatively compact in
is weakly relatively compact in  Using the fact that :
Using the fact that :

a standard trick of topology gives 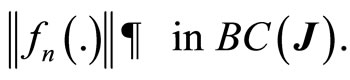
Lemma 3.5 Let, for a Banach space 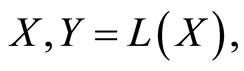 (the space of all bounded linear operators acting on X) and
(the space of all bounded linear operators acting on X) and  periodic. Then, for any given
periodic. Then, for any given 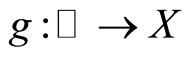 Eberlein-weakly almost periodic with a relatively compact range,
Eberlein-weakly almost periodic with a relatively compact range,

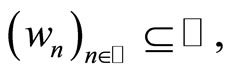
Proof. In Order to prove that 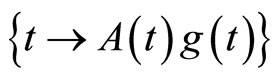 is Eberlein-weakly almost periodic, by W. M. Ruess and W. H. Summers’s criterion (2.4), we have to verify that for given sequences
is Eberlein-weakly almost periodic, by W. M. Ruess and W. H. Summers’s criterion (2.4), we have to verify that for given sequences 
 and
and 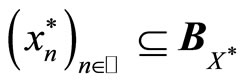
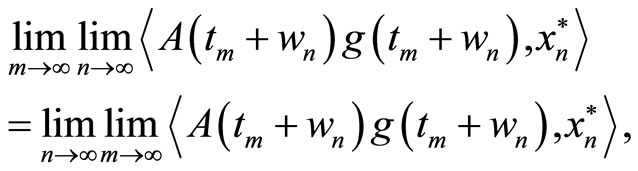
whenever the iterated limits exist. Assuming that the iterated limits exist and by the fact that we only have to prove the equality of them, we may pass to subsequences for the verification. Since g is Eberlein weakly almost periodic with a relatively compact range, by a use of a diagonalization routine, we may assume that
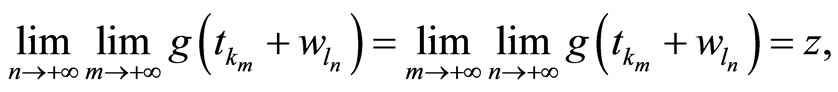
for a suitable choice of subsequences 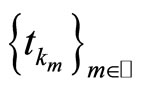 and
and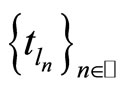 . We define
. We define
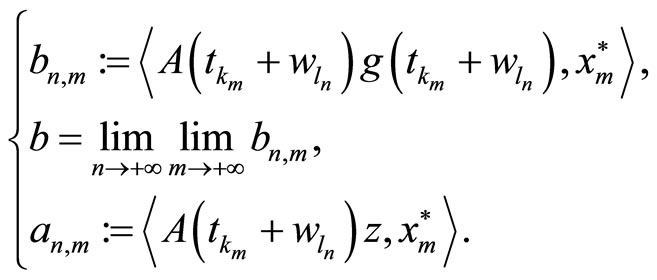
By hypothesis, we have 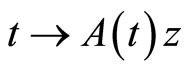 is periodic, thus
is periodic, thus 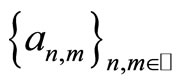 satisfies the double limits condition. Let
satisfies the double limits condition. Let  be the double limit.
be the double limit.
Now,
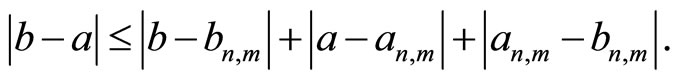
From the convergence of 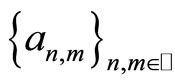 and
and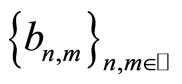 we derive that for every
we derive that for every  there exists an
there exists an 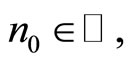 such that for
such that for 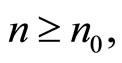 there exist an
there exist an 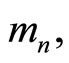 such that
such that
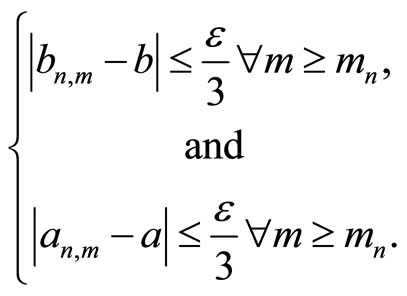
Using the double limits condition of the sequence , for given
, for given  there exists
there exists 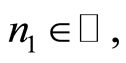 such that for all
such that for all  there is an
there is an 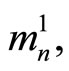 such that
such that
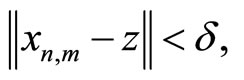 for all
for all 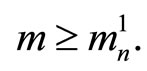 Applying the continuity of the map
Applying the continuity of the map  for
for  we find a
we find a 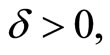 and according to the previous observation, there exists an
and according to the previous observation, there exists an 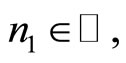 such that for all
such that for all 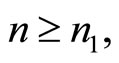 we find an
we find an  with
with

This yields, by a standard estimate, that  and hence
and hence 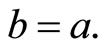
The following example shows that the compactness assumption on the range of g is essential and that the periodicity of 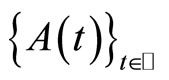 is not sufficient even if additional algebraic structure is given.
is not sufficient even if additional algebraic structure is given.
Example 3.6 We let 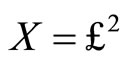 and choose
and choose
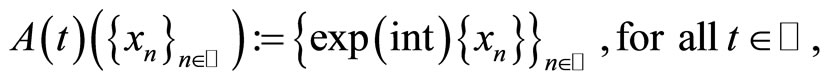
and 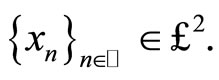
Further, if 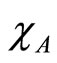 denotes the indicator function for the set A, we choose
denotes the indicator function for the set A, we choose 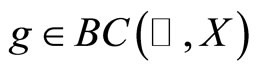
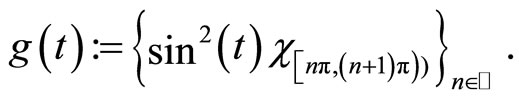
Using Lemma 2. 16 in ([13]), we obtain that g is Eberlein weakly almost periodic. Now, for the sequences
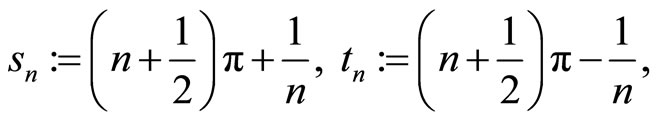
some calculations lead to the identity :

hence 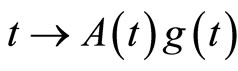 is not uniformly continuous, hence not Eberlein weakly almost periodic.
is not uniformly continuous, hence not Eberlein weakly almost periodic.
Proof. (of Theorem 3.2) Since f is Eberlein-weakly almost periodic, then f is continuous and bounded on . The existence and uniqueness of the bounded mild solution
. The existence and uniqueness of the bounded mild solution 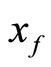 on
on  result of theorem (3.1).
result of theorem (3.1).
We claim that
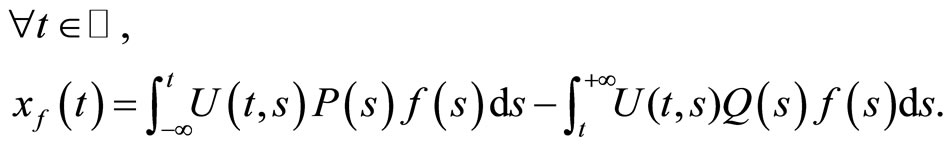 (2)
(2)
In fact, for any  we have
we have
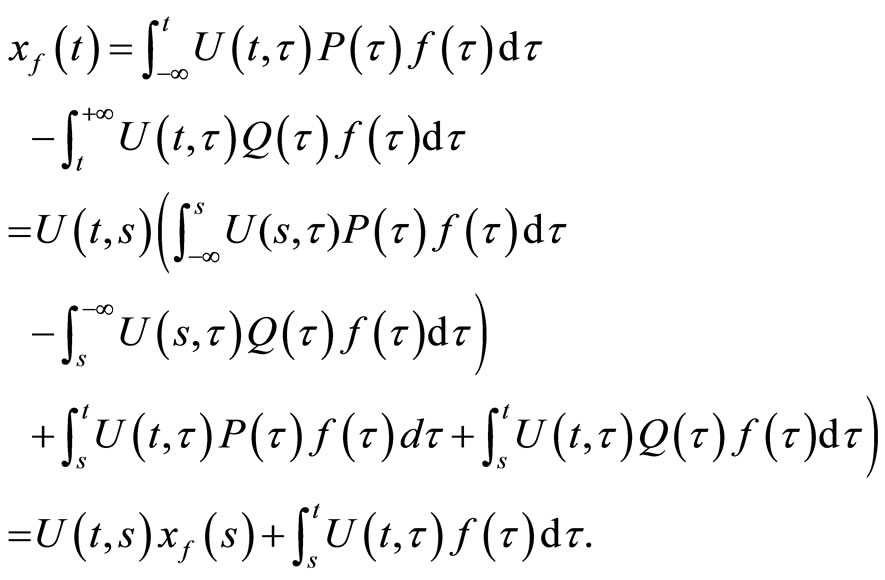
On the other hand, we have
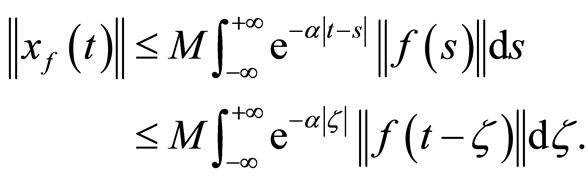
which ends the claim.
Now, to complete the proof, it remains for us to prove that 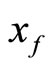 is Eberlein-weakly almost periodic. By Ruess and Summers’s double limits criterion, we have to verify that for given sequences
is Eberlein-weakly almost periodic. By Ruess and Summers’s double limits criterion, we have to verify that for given sequences
 and
and 
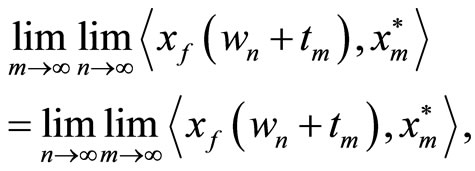
whenever the iterated limits exist. Assuming that the iterated limits exist and by the fact that we only have to prove the equality of them, we may pass to subsequences.
Since 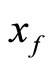 is uniformly continuous, by Lemma (3.3), we may assume that
is uniformly continuous, by Lemma (3.3), we may assume that  and
and 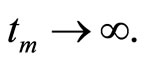 Furthermore without loss of generality
Furthermore without loss of generality 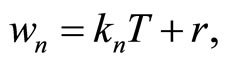 otherwise we have
otherwise we have  and by going over to subsequence
and by going over to subsequence  the uniform continuity gives us that the double limits for these both sequences coincide. Bringing the equality (2) into play we obtain:
the uniform continuity gives us that the double limits for these both sequences coincide. Bringing the equality (2) into play we obtain:
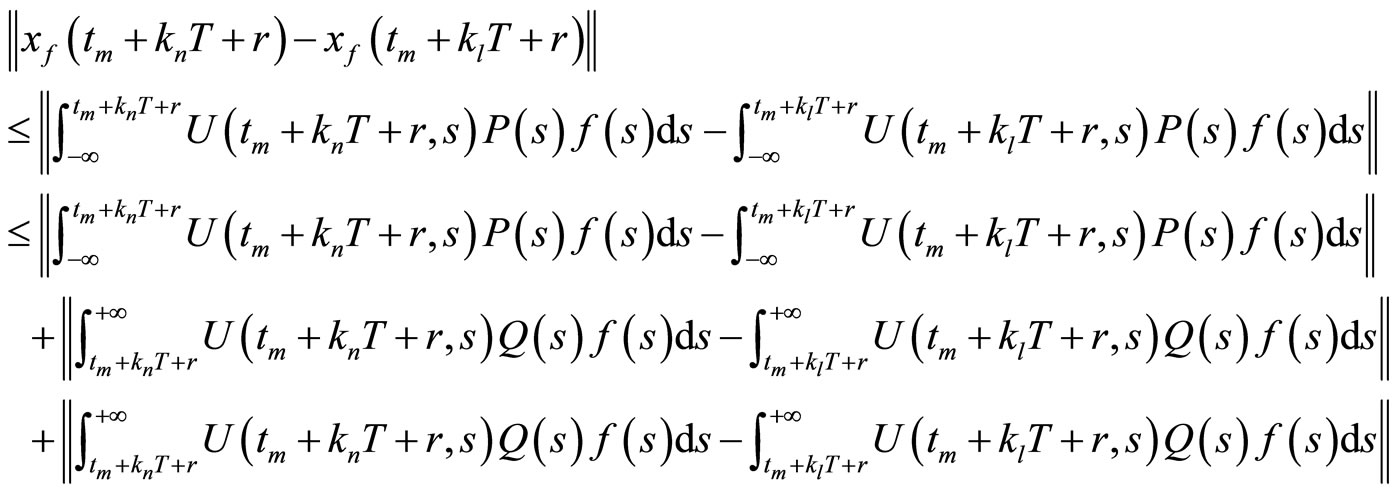
Since 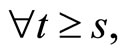
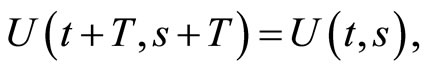 we obtain:
we obtain:
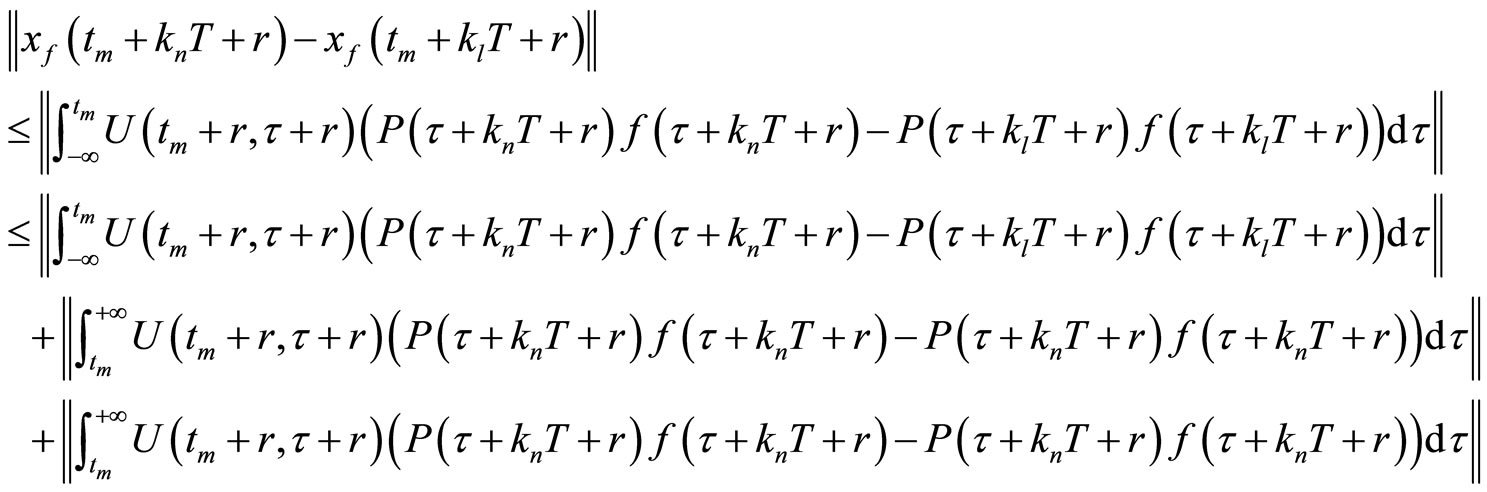
thus,
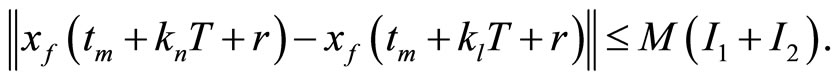
where
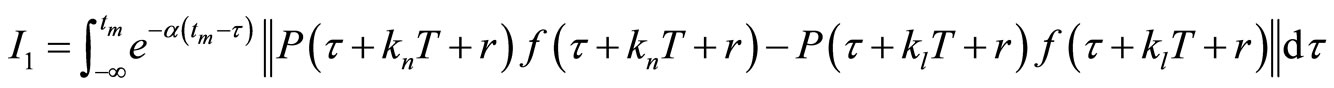
and
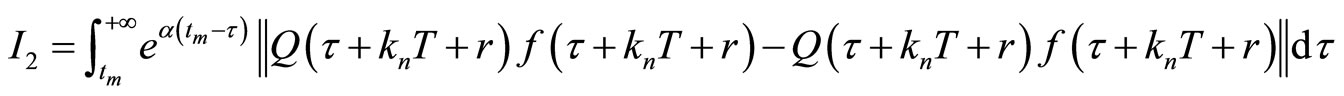
Since by Lemma (3.5)
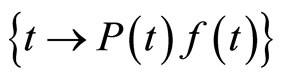
and
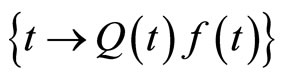
are Eberlein weakly almost periodic, we may assume that
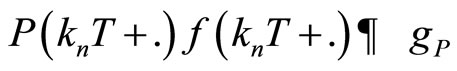
and
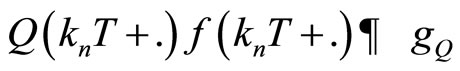
Bringing the last estimate into play we obtain
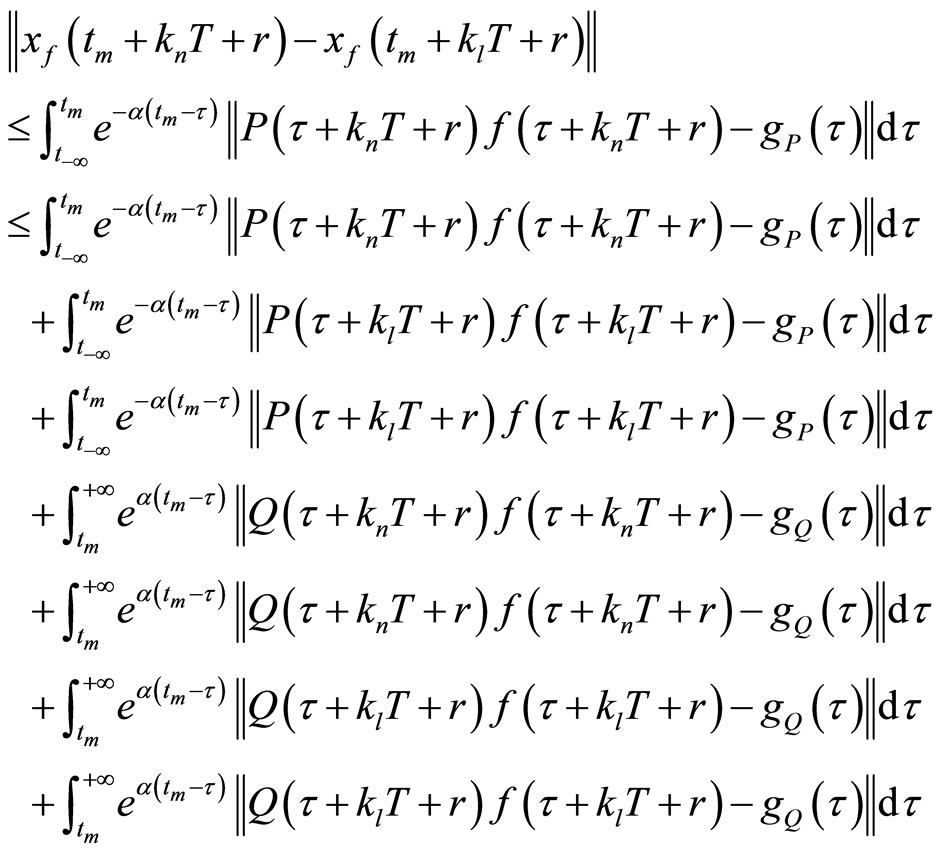
Thus,
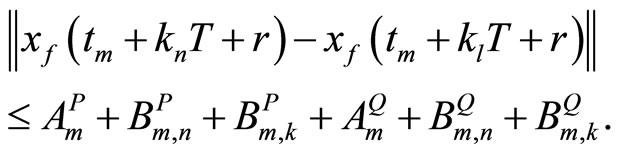
The uniform boundedness of the sequences of linear functional

and

and the fact that Lemma (3.4) applies to
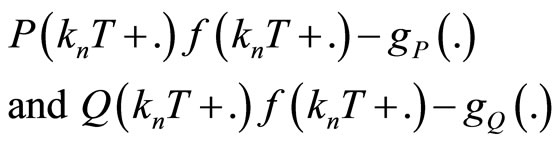
By going to appropriate subsequences, we can assume that the iterated double limits for 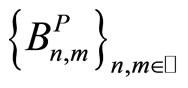 (resp. for
(resp. for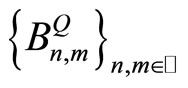 ) exist. Since they have to coincide, they have to be zero. By the triangle inequality we find,
) exist. Since they have to coincide, they have to be zero. By the triangle inequality we find,
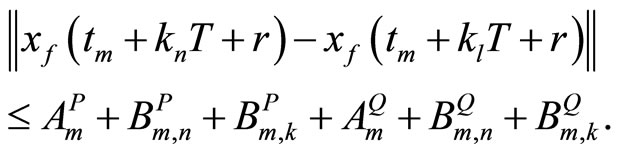
Starting with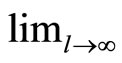 , then
, then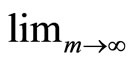 , and at last
, and at last , we obtain
, we obtain

which concludes the proof.
4. Acknowledgements
The authors would like to thank the I. R. D. (Institut de Recherche pour le Développement , UMI 209) for its hospitality and support.
REFERENCES
- C. Corduneanu, “Almost Periodic Functions,” Wiley, New York, 1968.
- A. M. Fink, “Almost Periodic Differential Equations,” Springer-Verlag, New York, 1974.
- C. Zhang, “Almost Periodic Type Functions and Ergodicity,” Science Press, Beijing; Kluwer Academic Publishers, Dordrecht, 2003.
- E. Ait Dads, “Contribution à l’existence de Solutions Presque Périodiques d’une Équation Fonctionnelle non Linéaire,” Thèse d’Etat, Faculté des Sciences Semlalia, Université Cadi Ayyad, Marrakech, 1994.
- E. Ait Dads and K. Ezzinbi, “Existence of Positive Pseudo-Almost-Periodic Solutions for Some Nonlinear Infinite Delay Integral Equations Arising in Epedimic Problems,” Nonlinear Analysis, Theory, Methods and Applications, Vol. 41, No. 1-2, 2002, pp. 1-13.
- E. Ait Dads and K. Ezzinbi, “Pseudo-Almost-Periodic Solutions for Some Delay Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 201, No. 3, 1996, pp. 840-850. doi:10.1006/jmaa.1996.0287
- W. F. Eberlein, “Eberlein Weak Almost Periodicity and Differential Equations in Banach Spaes,” Ph.D. Thesis, Universitat Essen, Germany, 1992.
- W. M. Ruess and W. H. Summers, “Weak Almost Periodicity and the Strongly Ergodic Limit Theorem for Conraction Semigroups,” Israel Journal of Mathematics, Vol. 64, 1988, pp. 139-157.
- W. M. Ruess and W. H. Summers, “Weak Almost Periodicity and the Strongly Ergodic Limit Theorem for Periodic Evolution Systems,” Journal of Functional Analysis, Vol. 94, No. 1, 1990, pp. 177-195. doi:10.1016/0022-1236(90)90033-H
- W. M. Ruess and W. H. Summers, “Weak Almost Periodic Semigroups of Operators,” Pacific Journal of Mathematics, Vol. 143, 1990, pp. 175-193.
- W. M. Ruess and W. H. Summers, “Integration of Asymptotically Almost Periodic Functions and Weak Asymptotic Almost Periodicity,” Dissertationes Mathematicae, Vol. 279, 1989.
- J. Kreulich, “Weakly Almost-Periodic Solutions of Evolution Equations in Banach Spaces,” Differential Integral Equations, Vol. 5, No. 9, 2011, pp. 1005-1027.
- J. Kreulich, “Eberlein-Weakly Almost-Periodicity Sand Differential Equations in Banach Spaces,” Ph.D. Thesis, University Essen, Germany, 1992.
- E. Ait Dads, K. Ezzinbi and S. Fatajou, “Weakly Almost Periodic Solutions for Some Differential Equations in a Banach Space,” Nonlinear Studies, Vol. 4, No. 2, 1997, pp. 157-170.
- E. Ait Dads, K. Ezzinbi and S. Fatajou, “Weakly Almost Periodic Solutions for the Inhomogeneous Linear Equations and Periodic Processes in a Banach Space,” Dynamic Systems and Applications, Vol. 6, 1997, pp. 507- 516.
- E. Ait Dads, K. Ezzinbi and S. Fatajou, “Asymptotic Behaviour of Solutions for Some Differential Equations in Banach Spaces,” African Diaspora Journal of Mathematics, Vol. 12, No. 1, 2011, pp. 1-18.
- H. Liu James, G. M. N’Guérékata and N. Van Minh, “Topics on Stability and Periodicity in Abstract Differential Equations,” Series on Concrete and Applicable Mathematics, Vol. 6, 2008.
- K. De Leeuw and I. Glicksberg, “Applications of Almost Periodic Compactifications,” Acta Mathematica, Vol. 105, No. 1-2, 1961, pp. 63-97. doi:10.1007/BF02559535
- K. De Leeuw and I. Glicksberg, “Almost Periodic Functions on Semigroups,” Acta Mathematica, Vol. 105, No. 1-2, 1961, pp. 99-140. doi:10.1007/BF02559536
- U. Krengel, “Ergodic Theorems,” De Gruyter Studies in Mathematical, 1985. doi:10.1515/9783110844641
- W. M. Ruess and W. H. Summers, “Ergodic Theorems for Semigroups of Operators,” Proceedings of the American Mathematical Society, Vol. 114, No. 2, 1992, pp. 423-432.
- A. Grothendieck, “Critères de Compacité dans les Espaces Fonctionnels Généraux,” American Journal of Mathematics, Vol. 74, No. 1, 1952, pp. 168-186. doi:10.2307/2372076
NOTES
*The authors were partially supported by the IRD project UMMISCO, UMI 209.

