Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19994 , 6 pages DOI:10.4236/am.2012.37103
Modeling of the Dissolved Oxygen in a River with Storage Zone on the Banks
1Department of Mathematics, Accurate Institute of Management and Technology, Greater Noida, India
2Department of Mathematics, Galgotia’s University, Greater Noida, India
3Centre for Atmospheric Sciences, Indian Institute of Technology (IIT), Delhi, India
Email: *nitash_kaushik@rediffmail.com
Received May 3, 2012; revised June 12, 2012; accepted June 19, 2012
Keywords: Mathematical Modeling; Dissolved Oxygen; Biochemical Oxygen Demand; Main Zone; Storage Zone
ABSTRACT
The prediction of water quality in terms of variables like dissolved oxygen (DO), biochemical oxygen demand (BOD), pH value, total dissolved solids (TDS) and salinity etc. is useful for evaluating the use of water for various related purposes. The widely used Streeter and Phelps models for computing biochemical oxygen demand and its impact on dissolved oxygen do not account for the settleable component of BOD and related implications. The model also does not account for the impact of storage zone on the stream’s DO. In the present work an attempt is made to develop a model which simultaneously accounts for the settleable component of BOD and the effect of storage zones on river’s DO. An application of the model to real field data suggests that the cumulative impact of settleable BOD and presence of storage zone in the river is to shift the critical deficit closer to the point source and magnify its amount.
1. Introduction
Dissolved Oxygen is the surrogate variable for the general health of an aquatic eco-system. Low dissolved oxygen in river adversely affects the aquatic system and consequently life of human being. The waste dumped into the river consumes the oxygen dissolved in river water for the process of stabilization. The amount of oxygen consumed by bacteria to stabilize the organic waste aerobically at a stated temperature and in specified period of time, called BOD, is used as an adjunct to DO determination.
The model presented by Streeter and Phelps 1925 [1] and subsequent mathematical formulation by Fair 1939 [2] are the first published mathematical models which were used to determine the DO condition in a stream below single point source under steady state conditions. The interesting characteristic of Streeter and Phelps model is the idea that the river may be represented by a single one-dimensional system. The model was well suited with the computational capabilities of that time, but it did not include that part of BOD which is in settleable form. This situation arises when partially treated/ untreated waste enters the river. Bhargava 1983, 1986(b) [3,4] incorporated the settleable part of BOD along with the soluble part and evaluated the model for accurate prediction of the DO-sag related parameters. Bhargava 1983, 1986(a) [3,5], however, did not include the dispersion term in his model. Tyagi et al. 1999 [6] accounted for both the parts of BOD in their model along with dispersion.
Various authors (Chapra and Runkel 1999 [7], Thackston and Schnelle 1970 [8], Gooseff 2005 [9]) explored and analyzed the impact of dead zone (also referred to as storage zone) in the last three decades. Several approaches have been developed to determine the impact of these storage zones on solute transport (Rutherford 1994 [10], Bencala & Walters 1983 [11], B. H. Schmid 1995 [12], R. L. Runkel 1998 [13] & S. K. Singh 2003 [14]). Bencala & Walters 1983 [11] suggested that a river is to be divided into two areas namely the main zone and storage zone.
The main zone is defined as that portion of the stream in which the advection and dispersion are the dominant transport mechanism, whereas the storage zone is that portion of the stream that contributes to transient storage. Water in storage zone is considered to be stationary relative to the water in main zone. Consequently, advection is not considered in the storage zone, while reaction and exchange of mass between the two zones are considered.
Chapra and Runkel 1999 [7] developed a steady state model that explicitly considers the effect of transient storage on DO below a point source of BOD containing only the dissolved part of BOD. The model illustrates the importance of inclusion of storage zone into stream and river water quality models. The model does not account for the BOD removal due to bioflocculation followed by sedimentation which invariably takes place after the discharge of partially treated sewage into the stream and hence the value of BOD and DO predicted by this model will not represent the actual river conditions in such cases.
The model presented by Chapra and Runkel 1999 [7] is extended to incorporate settleable part of BOD along with the dissolved part which represents the situation in which the partially treated/untreated waste enters the river having stagnant zone on the bank of river. The present work, therefore, addresses such a situation and develops a model to study the cumulative effect of stagnant zone and two types of BOD on river’s DO below a point source, under steady state condition.
2. Development of Model
A mathematical model is developed for the physical system as mentioned below.
2.1. Physical System
Consider a river in which there is an immobile storage zone on both the banks of river. Let the partially treated/ untreated oxygen demanding waste be released continuously at a constant rate into the river through a point source (waste treatment plant).
2.2. Mathematical Representation
The cross-section of the river is divided into two zone’s namely main zone in the centre of the river and storage zone along the two banks where the velocity is assumed to be zero. A mathematical model is developed for the above stated system based on the following assumptions.
• The entire BOD in the waste is in two forms namely dissolved and settleable. The dissolved part of BOD is decaying according to first order kinetics, while the settleable part of BOD is being removed by a linear law. The ratio of settleable part to total BOD is assumed to be fixed at the outfall.
• The size of storage zone is As and it consists of two parts located near the two banks of the river while the size of main zone is A which is located in the centre of river.
• No transverse gradient exists within any of the two zones. However, there is exchange of mass between the two zones which is linearly related to the difference in the respective concentrations.
• In the main zone, advection, reaction and exchange of mass are considered to be the relevant phenomena.
• In the storage zone only exchange of mass with the main zone and reaction within the storage zone are considered.
• In the storage zone the settleable BOD is settled at the outfall itself while in the main zone it is carried forward with the flow and is settled only after a particular distance downstream. Hence the effects of advective forces are considered and included in the transition time Ts, in which all the settleable part get removed from the waste. The transition time Ts = d/v would be longer for deeper rivers and for smaller flocculated particle size.
• Exchange of mass between two zones is considered only for dissolved part of BOD.
• The effect of reaeration is negligible in the storage zone, while in the main zone it is modeled according to Henry’s Law.
• The temperature effect on decomposition rates and oxygen saturation is same in each zone.
• There is no other source and sink of BOD and DO in the river.
Using the above stated assumptions, the steady-state mass balance equations for BOD and DO deficit in the main zone and storage zone respectively are given as follows:
Main-Zone
 (1)
(1)
 (2)
(2)
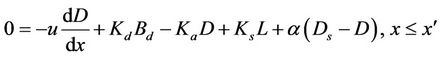 (3a)
(3a)
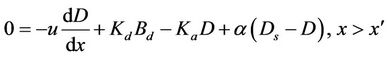 (3b)
(3b)
Storage Zone
 (4)
(4)
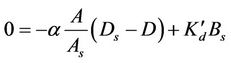 (5)
(5)
where Bd = dissolved part of BOD in main zone (mg/L); Bs = dissolved part of BOD in the storage zone (mg/L); L = Settleable part of BOD in main zone (mg/L); L0 = Initial settleable BOD in the main zone, D = DO deficit in the main zone (mg/L); Ds = DO deficit in the storage zone (mg/L); α = Storage zone exchange coefficient (per day); , is the distance at which all the settleable BOD is removed (m), u = Mean cross-sectional flow velocity (m/day); Kd = decomposition rate of dissolved BOD in the main zone (day−1);
, is the distance at which all the settleable BOD is removed (m), u = Mean cross-sectional flow velocity (m/day); Kd = decomposition rate of dissolved BOD in the main zone (day−1); 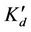 = decomposition rate of dissolved BOD in the storage zone (day−1); Ks = decomposition rate of settleable BOD in the main zone, Ka = coefficient of reaeration in the main zone (day−1); v = Settling velocity of particles (m/day); d = Depth of the river (m).
= decomposition rate of dissolved BOD in the storage zone (day−1); Ks = decomposition rate of settleable BOD in the main zone, Ka = coefficient of reaeration in the main zone (day−1); v = Settling velocity of particles (m/day); d = Depth of the river (m).
2.3. Boundary Conditions
The associated boundary conditions reflecting the release of BOD causing material are  and
and 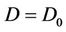 at
at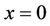 .
.
3. Method of Solution
The value of Bs computed from Equation (4) as follows:
 (6)
(6)
Bs is substituted in Equation (1) to give the following equation
 (7)
(7)
where
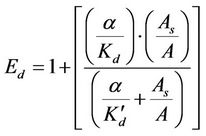
Ed can be identified as a dimensionless enhancement factor representing the impact of the storage zone on decomposition.
Let 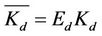 where
where  an apparent decomposition ratio that accounts for the storage-zone (per-day).
an apparent decomposition ratio that accounts for the storage-zone (per-day).
Equation (6) now converts to
 (8)
(8)
with the boundary condition  at
at . On solving (8), we get
. On solving (8), we get
 (9)
(9)
So that the total BOD (BM) in the main zone is given by the following equations
 (10a)
(10a)
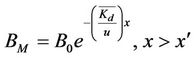 (10b)
(10b)
Using Equations (6), (10a) and (10b), then the total BOD in the storage zone is given by
 (11a)
(11a)
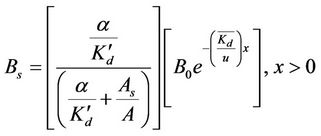 (11b)
(11b)
From Equation (5), we get
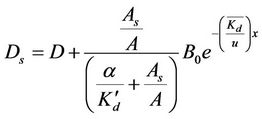 (12)
(12)
The value of Ds when substituted in Equation (3a), yields
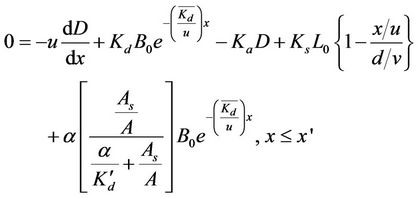 (13a)
(13a)
On solving Equation (13a) with the boundary condition  at
at , we get
, we get
 (13b)
(13b)
The value of Ds when substituted in Equation (3b), yields
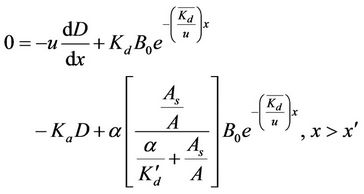 (14a)
(14a)
On solving Equation (14a) with the boundary condition  at
at , we get
, we get
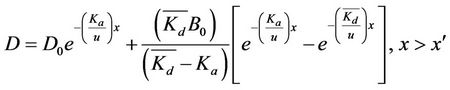 (14b)
(14b)
Using Equations (12), (13b) & (14b), the value of DOdeficit in the storage zone represented by Ds is given as follows:
 (15)
(15)
 (16)
(16)
The dissolved oxygen in both the zones represented by C and Cs respectively is then computed as follows, 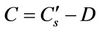 in the main zone and
in the main zone and  in the storage zone, where
in the storage zone, where 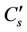 and
and 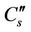 are the value of DO at saturation level in the main zone and the storage zone respectively.
are the value of DO at saturation level in the main zone and the storage zone respectively.
4. Results and Discussion
To analyze the cumulative impact of settleable BOD and storage zone on river’s DO, the model is applied to Uvas Creek for which the physical parameters with their values are outlined in Table 1.
To predict the concentration of DO in the considered river system, some kinetic and chemical parameters are appropriately taken from the literature and their values are given in Table 2. The model is applied to simulate a 3 Km stretch of the Creek along with the present model, The result of conventional S-P model and storage zone version of S-P model (presented by Chapra) are also displayed for comparison.
Case 1: The entire BOD is in dissolved form and the Creek has no storage zone(S-P model).
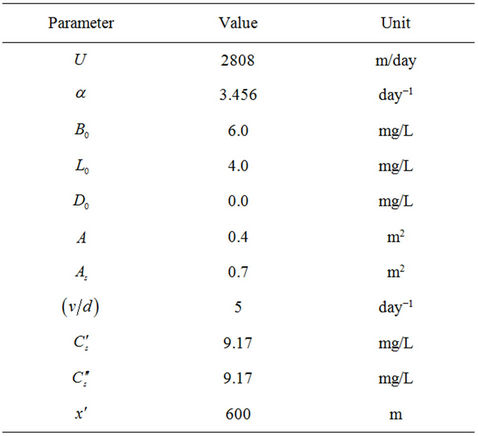
Table 1. Hydraulic parameters.
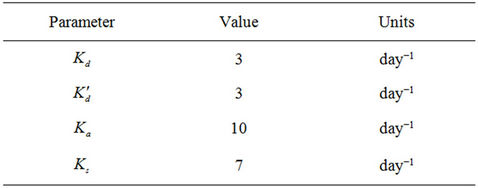
Table 2. Chemical and kinetic parameters.
Case 2: The entire BOD is in dissolved form and the Creek has storage zone (Chapra’s model).
Case 3: A part of total BOD is in settleable form and the Creek has storage zone (The present model).
Figure 1 depicts the comparative BOD distribution in the main zone as predicted by the conventional StreeterPhelps model, Streeter-Phelps storage zone model (i.e. Chapra’s model) and the present model. It is observed from the figure that the concentration of BOD by the present model is less than that predicted by S-P model as well as the Chapra’s model. Since the presented model includes the storage zone which increases the residence time of pollutant in the river resulting in increased BOD assimilation. Furthermore, due to the presence of settleable part, BOD assimilation would be at a faster rate in the initial stretch of the Creek. The cumulative effect of presence of storage zone and settleable part would be more and faster BOD assimilation in the initial stretch (here 600 m) and consequently lesser concentration of remaining BOD is observed in the comparative plots in Figure 1.
Figure 2 depicts the similar plots for all the three cases to compare the distribution of DO with distance downstream in the main zone. It is observed that the concentration of DO as predicted by the present model is

Figure 1. Main zone BOD (Present model vs Chapra’s model and Streeter-Phelps model).

Figure 2. Main zone DO (Present model vs Chapra’s model and Streeter-Phelps model).
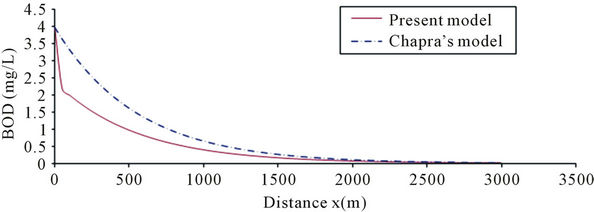
Figure 3. Storage zone BOD (Present model vs Chapra’s model).

Figure 4. Storage zone DO (Present model vs Chapra’s model).
less than that predicted by both Chapra’s model and S-P model in the main zone. Since all other factors affecting the river’s DO being the same everywhere, the greater and faster demand would consume more DO at a faster rate and consequently the DO would decrease more rapidly with increased amount of BOD exertion. Since the DO deficit is more in the presented model, the recovery of DO from atmosphere would be faster as per the Henry’s law. The plots in Figure 2 adequately justify this reasoning.
Figure 3 depicts the comparative BOD distribution in the storage zone as predicted by the Streeter-Phelps storage zone model (i.e., Chapra’s model) and the present model. It is observed from the figure that for the beginning stretch (0 - 50 meters) of the downstream the concentration of BOD by the present model is very less than the concentration of BOD by Chapra’s model. Because the settleable part of BOD in the present model settled at the starting point of downstream, so the remaining BOD of present model is very less than the remaining BOD of Chapra’s model. And the difference of concentration of BOD of two models becomes less gradually with the distance downstream.
Figure 4 depicts the comparative dissolved oxygen
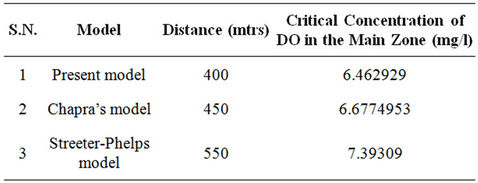
Table 3. Critical concentration of DO in the main zone.
(DO) distribution in the storage zone as predicted by Streeter-Phelps storage zone model (i.e., Chapra’s model) and the present model. It is observed from the figure that for the beginning stretch (0 - 50 meters) of the downstream, the dissolved oxygen by the present model is very high compared to the dissolved oxygen by Chapra’s model. Because the settleable part of BOD in the present model settled at the starting point of downstream, so the remaining BOD of the present model is very less than the remaining BOD of Chapra’s model. Since all other factors affecting the river’s DO being the same everywhere, the less demand would consume less DO and consequently the DO would increase with decreased amount of BOD exertion.
The cumulative impact of settleable part of BOD in the waste water and presence of the storage zone in the river is to reduce the DO concentration at every point at a distance downstream and to move the critical deficit closer to the point source. Table 3 gives a comparison for the concentration and location of critical DO for all the three models used in comparative study.
5. Conclusion
It is concluded that predicting the distribution of DO in the river with the storage zone on the two banks depends on the treatment of waste. If untreated or partially treated waste enters such river then the model presented by Chapra shall be of little use. The present model would be able to predict the DO conditions more accurately and consequently the decision based on such a prediction would be more rational for such a real life situation.
REFERENCES
- H. W. Streeter and E. B. Phelps, “A study of the Pollution and Natural Purification of the Ohio Rivers,” US Public Health Service Bulletin No. 146, 1925.
- G. M. Fair, “The Dissolved Oxygen Sag—An Analysis,” Sewage Works Journal, Vol. 11, No. 3, 1939, p. 445.
- D. S. Bhargava, “Most Rapid BOD Assimilation in Ganga and Yamuna Rivers,” Journal of Environmental Engineering, Vol. 109, No. 1, 1983, pp. 174-187. doi:10.1061/(ASCE)0733-9372(1983)109:1(174)
- D. S. Bhargava, “Models for Polluted Streams Subject to Fast Purification,” Water Research, Vol. 20, 1986, pp. 1-8.
- D. S. Bhargava, “DO Sag Model for Extremely Fast River Purification,” Journal of Environmental Engineering, Vol. 112, 1986, pp. 572-585.
- B. Tyagi, S. Gakkhar and D. S. Bhargava, “Mathematical Modeling of Stream DO-BOD Accounting for Settleable BOD and Periodically Varying BOD Source,” Environmental Software, Vol. 14, 1999, pp. 461-471.
- S. C. Chapra and R. L. Runkel, “Modeling Impact of Storage Zones on Stream Dissolved Oxygen,” Journal of Environmental Engineering, Vol. 125, No. 5, 1999, pp. 415-419. doi:10.1061/(ASCE)0733-9372(1999)125:5(415)
- E. L. Thacksten and K. B. Schnelle, “Predicting Effects of Dead Zone on Stream Mixing,” Sanitary Engineering, Vol. 96, 1970, pp. 319-331.
- M. N. Gooseff, “Determining in Channel (Dead Zone) Transient Storages by Solute Transport in a Bedrock Channel-Alluvial Channel, Sequence Oregon,” Water Resource Research, Vol. 41, 2005, W06014. doi:10.1029/2004WR003513
- J. C. Rutherford, “River Mixing,” Wiley, New York, 1994.
- K. E. Bencala and R. A. Walters, “Simulation of Solute Transport in a Mountain Pool-and-Riffle Stream: A Transient Storage Model,” Water Resource Research, Vol. 19, No. 3, 1983, pp. 718-724. doi:10.1029/WR019i003p00718
- B. H. Schmid, “On the Transient Storage Equations for Longitudinal Solute Transport in Open Channels: Temporal Moments Accounting for the Effects of First-Order Decay,” Hydraulic Research, Vol. 33, No. 5, 1995, pp. 595-609. doi:10.1080/00221689509498559
- R. L. Runkel, “One Dimensional Transport with Inflow and Storage (OTIS): A Solute Transport Model for Streams and Rivers,” US Geological Survey, Water Resources Investigation Report 98-4018, 1998, p. 73.
- S. K. Singh, “Treatment of Stagnant Zone in Riverine Advection Dispersion,” Journal of Hydraulic Engineering, Vol. 129, No. 6, 2003, pp. 470-473. doi:10.1061/(ASCE)0733-9429(2003)129:6(470)
NOTES
*Corresponding author.

