Applied Mathematics
Vol. 3 No. 4 (2012) , Article ID: 18877 , 3 pages DOI:10.4236/am.2012.34048
Some Problems on Best Approximation in Orlicz Spaces*
1College of Mathematics Science, Inner Mongolia Normal University, Huhhot, China
2College of Natural Science, Inner Mongolia Agricultural University, Huhhot, China
Email: wgrd@imnu.edu.cn, 494777843@qq.com
Received January 17, 2012; revised February 19, 2012; accepted February 26, 2012
Keywords: Chebyshev System; Haar Subspace; Orlicz Space; Best Approximation
ABSTRACT
In this paper we studied some problems on best approximation in Orlicz spaces, for which the approximating sets are Haar subspaces, the result of this paper can be considered as the extension of the classical corresponding result.
1. Introduction
Let 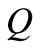 be a compact Hausdorff space,
be a compact Hausdorff space,  be all the continuous functions on
be all the continuous functions on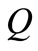 . There are at least
. There are at least 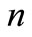 points on
points on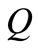 ,
, . Define
. Define
 as
as 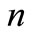 order Chebyshev system if for arbitrary vector
order Chebyshev system if for arbitrary vector ,
,
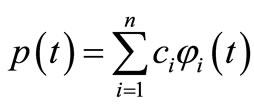 has at most
has at most  zero points on Q [1].
zero points on Q [1].
Define the linear subspace

which is spanned by  order Chebyshev system as a Haar subspace of
order Chebyshev system as a Haar subspace of  [1].
[1].
In this paper, let  and
and 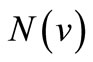 be mutually complementary
be mutually complementary 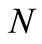 function. The definition and properties of
function. The definition and properties of  function can be seen in [2]. The Orlicz space
function can be seen in [2]. The Orlicz space  corresponding to the N function
corresponding to the N function 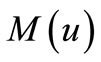 consists of all Lebesgue measurable functions
consists of all Lebesgue measurable functions 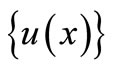 on
on , of which the Orlicz norm
, of which the Orlicz norm
 (1.1)
(1.1)
is finite, here

is the modulus of  corresponding to
corresponding to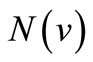 . According to [2], the Orlicz norm (1.1) can also be calculated by
. According to [2], the Orlicz norm (1.1) can also be calculated by
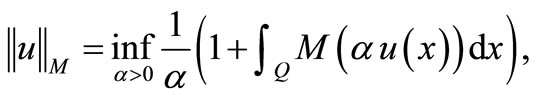 (1.2)
(1.2)
and there exists an , satisfying
, satisfying
 shch that
shch that

here 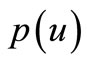 is the derivative of
is the derivative of  on the right. Equivalent to the Orlicz norm (1.1), in Orlicz space
on the right. Equivalent to the Orlicz norm (1.1), in Orlicz space , the Luxemburg norm is defined by
, the Luxemburg norm is defined by
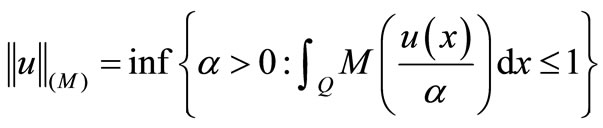 . (1.3)
. (1.3)
In the sequel 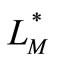 and
and 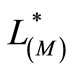 will denote the Orlicz space with Orlicz norm (1.1) and the Luxemburg norm (1.3) respectively.
will denote the Orlicz space with Orlicz norm (1.1) and the Luxemburg norm (1.3) respectively.
It is well known that
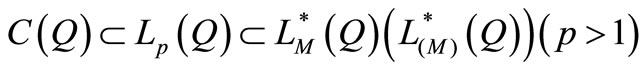 .
.
2. Main Results
Now we choose 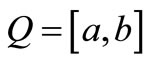 and
and 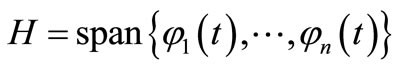 is a Haar subspace of
is a Haar subspace of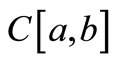 , then we obtain Theorem 1. Let
, then we obtain Theorem 1. Let  be
be  function satisfying
function satisfying  condition, of which the derivative on the right
condition, of which the derivative on the right 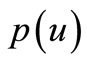 is continuous and strictly monotone increasing,
is continuous and strictly monotone increasing,  ,
,  , if
, if 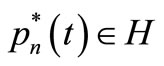 is the best approximator in the mean of
is the best approximator in the mean of 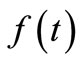 in
in 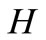 for the Orlicz norm
for the Orlicz norm 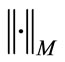 or the Luxemburg norm
or the Luxemburg norm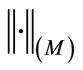 , then there exist at least
, then there exist at least  different zero points of
different zero points of  in
in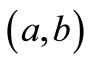 .
.
In order to prove this theorem, first we state the following two lemmas.
Lemma 1. [3-5]. Let  be N function satisfying
be N function satisfying 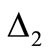 condition, of which the derivative on the right
condition, of which the derivative on the right  is continuous and strictly monotone increasing, F is a linear subspace of
is continuous and strictly monotone increasing, F is a linear subspace of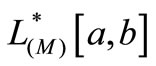 ,
,  then
then  is the best approximator in the mean of
is the best approximator in the mean of 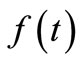 in
in  for the Luxemburg norm
for the Luxemburg norm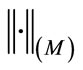 , if and only if for arbitrary function
, if and only if for arbitrary function ,
,
 holds true.
holds true.
Lemma 2. [4,5]. Under the conditions of lemma 1, 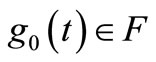 is the best approximator in the mean of
is the best approximator in the mean of 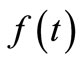 in
in 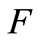 for the Orlicz norm
for the Orlicz norm , if and only if for arbitrary function
, if and only if for arbitrary function ,
,
 holds true, here
holds true, here  satisfies
satisfies
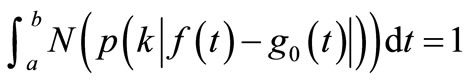 .
.
Proof of Theorem 1. We prove first the case of the Luxemburg norm. Here we take reduction to absurdity. Assume there exist at most  different zero points
different zero points 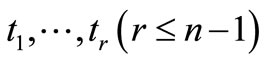 of
of  in
in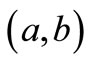 . Based on
. Based on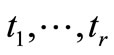 , we choose
, we choose 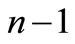 points in
points in , such that
, such that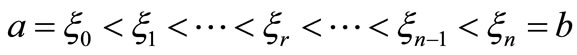 , here
, here ,
,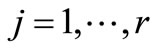 . From lemma 1 we get
. From lemma 1 we get
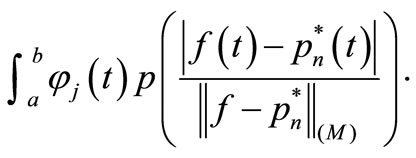
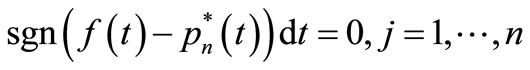 .
.
For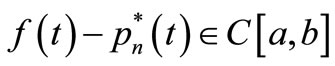 , the above can be deduced as following
, the above can be deduced as following

here every 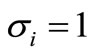 or
or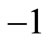 ,
,

According to the theory of system of linear equationswe have that , hence the transposed system of equations
, hence the transposed system of equations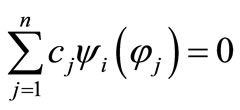 ,
,  also has a nonzero solution
also has a nonzero solution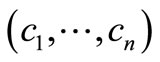 . Set
. Set 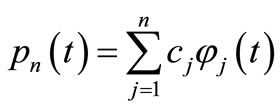 , then
, then  for some
for some . On the other hand,
. On the other hand,
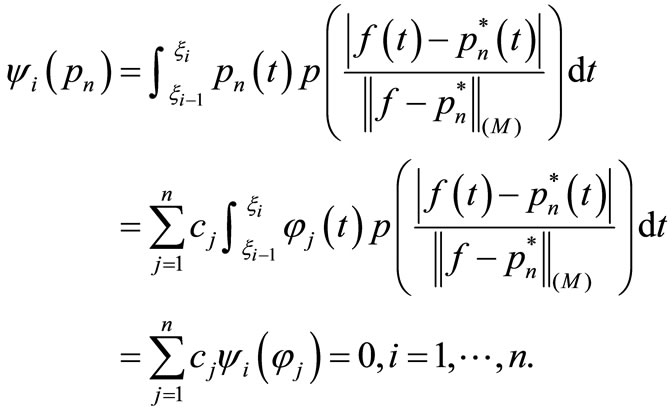
Since 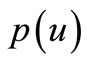 is the derivative of
is the derivative of 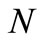 function
function 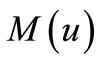 on the right, according to the properties of
on the right, according to the properties of 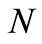 function (see [2]) and the hypothesis of
function (see [2]) and the hypothesis of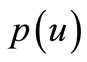 , we obtain
, we obtain
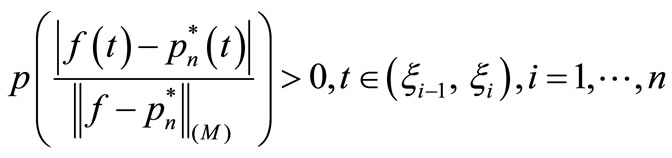 .
.
The above shows that there exist zero points of the continuous function 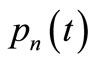 in every interval
in every interval 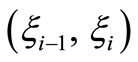
 , that is to say,
, that is to say,  has at least
has at least  different zero points in interval
different zero points in interval . Since
. Since 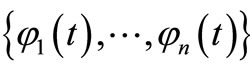 is
is  order Chebyshev system, we get
order Chebyshev system, we get , Together with the previous result, we get a contradiction.
, Together with the previous result, we get a contradiction.
In an analogous way, following lemma 2 we can also prove the case of the Orlicz norm.
In the sequel we choose ,
,  ,
, 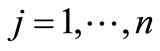 , then the Haar subspace of
, then the Haar subspace of  is
is , consists of all algebraic polynomials of order not larger than
, consists of all algebraic polynomials of order not larger than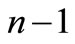 . For
. For , in order to solve the problem of best approximation of
, in order to solve the problem of best approximation of 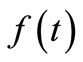 with
with  in Orlicz space, actually we just need to consider the problem of the minimal norm of monic polynomials of order
in Orlicz space, actually we just need to consider the problem of the minimal norm of monic polynomials of order  in Orlicz space, that is, to consider the extreme value problems as following
in Orlicz space, that is, to consider the extreme value problems as following
 ; (2.1)
; (2.1)
 . (2.2)
. (2.2)
The similar problems in  space has not been completely solved except
space has not been completely solved except  (see [6]). In Orlicz spaces the problems have not been studied yet. Here we obtain Theorem 2. Let
(see [6]). In Orlicz spaces the problems have not been studied yet. Here we obtain Theorem 2. Let  be
be  function satisfying
function satisfying 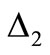 condition, its graph do not contain any straight line segment, its derivative on the right
condition, its graph do not contain any straight line segment, its derivative on the right 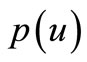 be continuous and strictly monotone increasing, then 1) The extreme value problems (2.1) and (2.2) have unique solution respectively, that is, there exist unique group
be continuous and strictly monotone increasing, then 1) The extreme value problems (2.1) and (2.2) have unique solution respectively, that is, there exist unique group 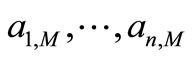 and
and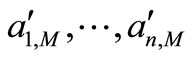 , shch that
, shch that
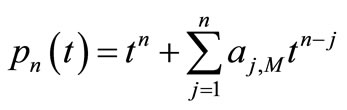
and

satisfy
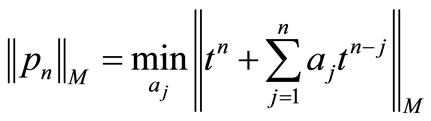 ;
;
 here
here  and
and 
 depend on
depend on 
function  corresponding to the Orlicz space.
corresponding to the Orlicz space.
2) The extremal functions  and
and 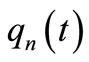 have n different zero points in
have n different zero points in 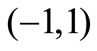 respectively.
respectively.
3) The odevity of extremal functions 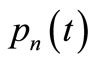 and
and 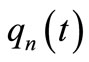 is same to the odevity of natural number
is same to the odevity of natural number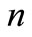 .
.
Proof. 1) From [2] (pp. 160-168), we know, under the conditions of theorem 2, Orlicz spaces 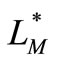 and
and 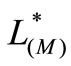 are strictly convex. Since
are strictly convex. Since  is a finite dimensional linear subspace, (1) is obvious by the theory of best approximation (see [1], pp. 1-10).
is a finite dimensional linear subspace, (1) is obvious by the theory of best approximation (see [1], pp. 1-10).
2) From Theorem 1 we can easily obtain it.
3) Since  function
function 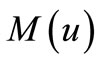 is an even function, so
is an even function, so

Analogously,
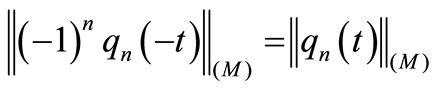
holds true. Hence, from (1), the uniqueness of the extremal function, we obtain
 ;
;
 .
.
By these, (3) follows.
3. Acknowledgements
This work is supported by the National Natural Science Foundation of China under the contracts No. 11161033 and the Natural Science Foundation of Inner Mongolia Autonomous Region under the contracts No. 2009MS0105.
REFERENCES
- Y. S. Sun, “Approximation Theory of Functions,” Beijing Normal University Press, Beijing, 1989.
- C. X. Wu and T. F. Wang, “Orlicz Space and Its Applications,” Hei Long Jiang Science and Technology Press, Harbin, 1983.
- D. L. Xie, “The Characteristics of Best Approximators in Orlicz Spaces,” Journal of Hangzhou University, Vol. 12, No. 3, 1985, pp. 319-322.
- Y. W. Wang and S. T. Chen, “The Best Approximating Operators in Orlicz Spaces,” Pure Mathematics and Applied Mathematics, Vol. 2, No. 2, 1986, pp. 44-51.
- C. X. Wu, T. F. Wang, S. T. Chen and Y. W. Wang, “The Geometric Theory of Orlicz Spaces,” Harbin Industrial University Press, Harbin, 1986.
- J. Gillis and G. Lewis, “Monic Polynomials with Minimal Norm,” Journal of Approximation Theory, Vol. 34, No. 2, 1982, pp. 187-193. doi:10.1016/0021-9045(82)90091-0
NOTES
*Supported by the NSFC (11161033).

