Applied Mathematics
Vol.3 No.3(2012), Article ID:18089,3 pages DOI:10.4236/am.2012.33033
Asymptotic Behaviour to a Von Kármán System with Internal Damping
1Departament of Mathematics, Pará State University, UEPA, Belém, Brazil
2Departament of Mathematics, Federal University of São João Del-Rei, UFSJ, São João Del-Rei, Brazil
3Departament of Mathematics, Federal University of Pará, UFPA, Belém, Brazil
Email: *raposo@ufsj.edu.br
Received December 13, 2011; revised February 13, 2012; accepted February 21, 2012
Keywords: Von Kármán System; Internal Damping; Exponential Decay; Theorem of Nakao
ABSTRACT
In this work we consider the Von Kármán system with internal damping acting on the displacement of the plate and using the Theorem due to Nakao [1] we prove the exponential decay of the solution.
1. Introduction
Theodor von Kármán (1910) [2] started the nonlinear system of partial differential for great deflections and for the Airy stress function of a thin elastic plate. For several years this system was studied in different situations. Using frictional dissipation at boundary, I. Lasiecka et al. [3-5] proved the uniform decay of the solution. G. P. Menzala and E. Zuazua [6] by semigroup properties gave the exponential decay when thermal damping was considered. For Viscoelastic plates with memory, J. E. M. Rivera et al. [7,8] proved that the energy decays uniformly, exponentially or algebraically with the same rate of decay of the relaxation function. C. A. Raposo and M. L. Santos [9] gave a General Decay of solution for the memory case. In [10-13] the authors consider the von Kármán system with frictional dissipations effective in the whole plate, in a part of the plate or at the boundary. It is shown in these works that these dissipations produce uniform rate of decay of the solution when t goes to infinity. In this work we also consider the system with internal damping, which is the natural problem. A distinctive feature of our paper is to use Nakao’s method to show that the energy decays exponentially to zero.
2. Existence of Solution
We use the standard Lebesgue space and Sobolev space with their usual properties as in [14] and in this sense 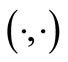 and
and  denotes the inner product in
denotes the inner product in 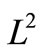 and
and 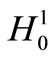 respectively and by
respectively and by  we denote the usual norm in
we denote the usual norm in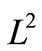 . Let
. Let 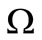 be a bounded domain of the plane with regular boundary
be a bounded domain of the plane with regular boundary![]() . For a real number
. For a real number 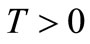 we denote
we denote 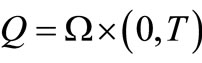 and
and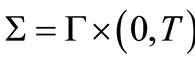 . Here
. Here 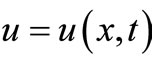 is the displacement,
is the displacement, 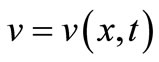 the Airy stress function and
the Airy stress function and 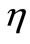 is the unit normal external in
is the unit normal external in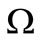 . With this notation we have the following system
. With this notation we have the following system
 (1)
(1)
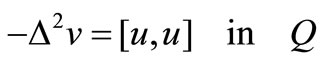 (2)
(2)
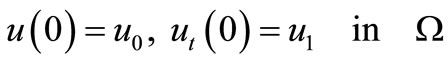 (3)
(3)
 (4)
(4)
where
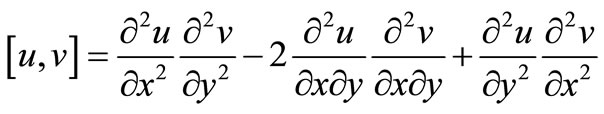
Now using the same idea of [6] we have the following result of existence of solution.
Theorem 2.1. For 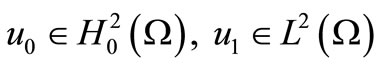 there exists
there exists 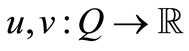 such that
such that
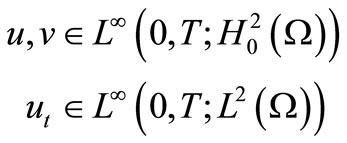
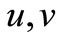 weak solution of (1)-(4).
weak solution of (1)-(4).
Proof. We defining the energy  of the system (1)-(4) by
of the system (1)-(4) by
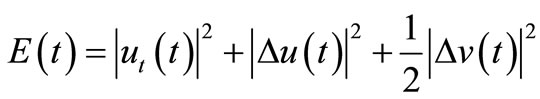 .
.
This system is well posed in the energy space (see [15]) and we have and E’(t) < 0. Galerkin’s method together with the dissipative properties of the energy give us global existence of solution in the energy space. Finally using the results from [5] on the regularity properties of von Kármám bracket the uniqueness follows.
3. Asymptotic Behaviour
In this section, we will use the Theorem of Nakao to prove the exponential decay of the solution.
Theorem 3.1. (Theorem of Nakao) Let 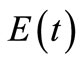 be a nonnegative function on
be a nonnegative function on 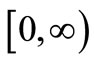 satisfying
satisfying
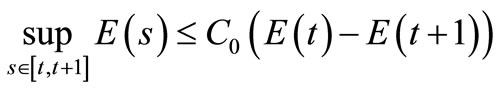
where 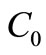 is a positive constant. Then we have
is a positive constant. Then we have
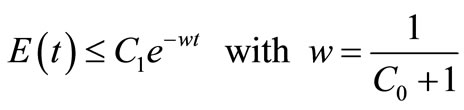 .
.
Proof. See page 748 of [1].
In the sequel we have two lemmasLemma 3.1. The functional 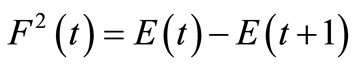 satisfies
satisfies
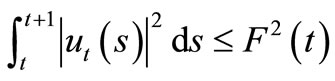 .
.
Proof. Multiplying (1) by  and integrating in
and integrating in , we have
, we have
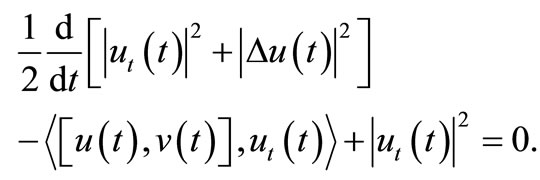
Using (2) we obtain
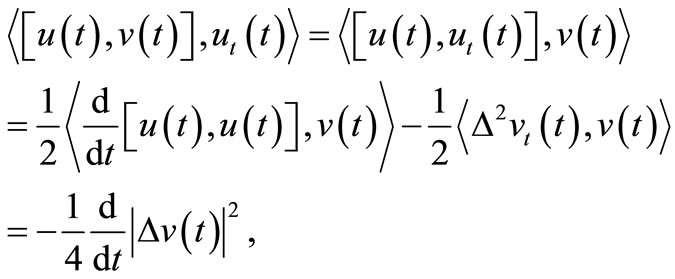
from where follows
 (5)
(5)
Performing integration in , we have
, we have
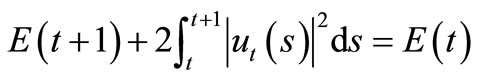 (6)
(6)
then
 . (7)
. (7)
Lemma 3.2. The functional
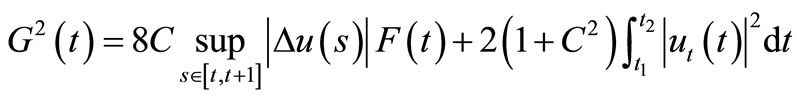
satisfies
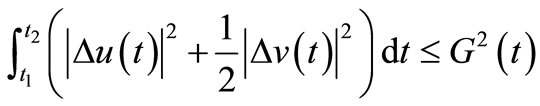 .
.
Proof. First we note that
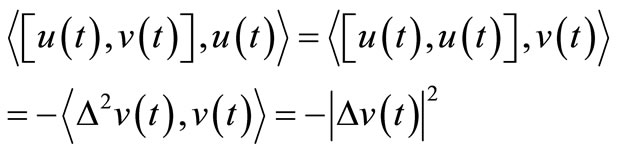 (8)
(8)
From (7) we get  and
and 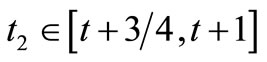 such that
such that
 . (9)
. (9)
Multiplying (1) by u and integrating in , we have
, we have
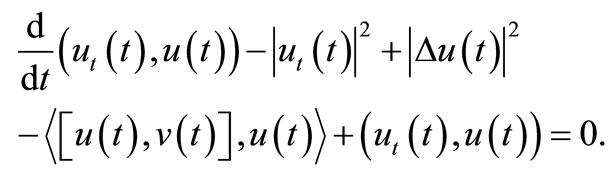
Integrating from  to
to ![]() and using (8) we have
and using (8) we have
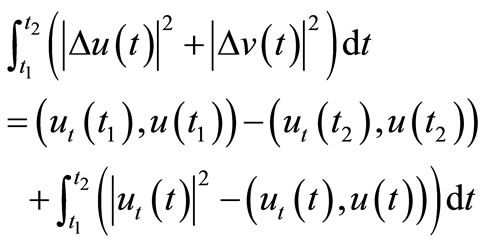
Now, choosing C such that 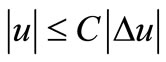 and applying Cauchy-Schuwarz inequality we get
and applying Cauchy-Schuwarz inequality we get
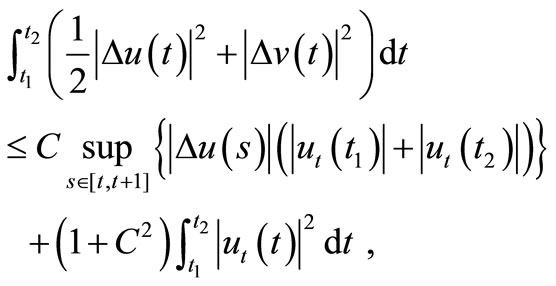
and using (9),
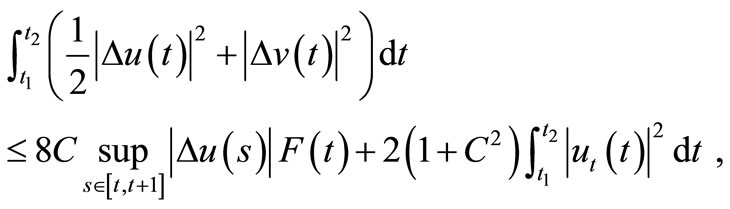
from where follows
 . (10)
. (10)
Now we are in position of to prove our principal result.
Theorem 3.2. The solution 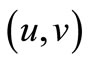 satisfies
satisfies
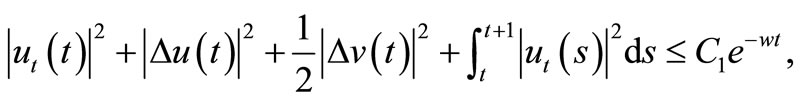 (11)
(11)
for almost every , with
, with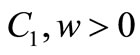 , constants independents from t.
, constants independents from t.
Proof. From (7) and (10) we obtain
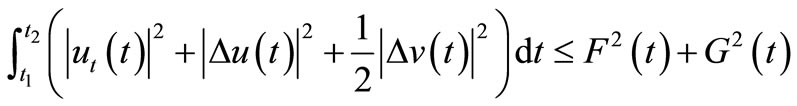 .
.
There exists 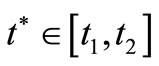 such that
such that
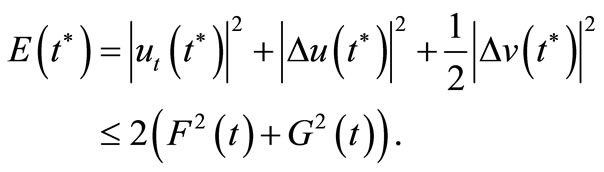 (12)
(12)
From (6) we get
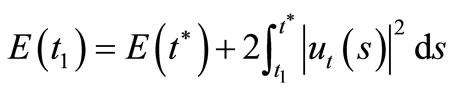 .
.
Then

and
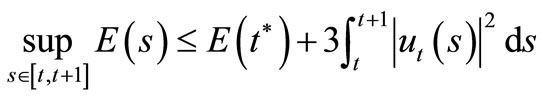
Now using (11) and (12) we obtain

then
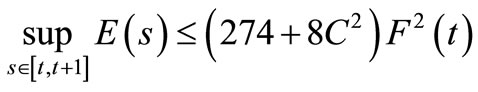 and finally by Theorem of Nakao follows
and finally by Theorem of Nakao follows

with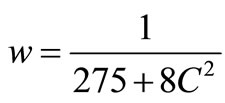 .
.
REFERENCES
- M. Nakao, “A Difference Inequalit and Its Application to Nonolinear Evolution Equation,” Journal of the Mathematical Society of Japan, Vol. 30, No. 4, 1978, pp. 747-762. doi:10.2969/jmsj/03040747
- T. V. Kármán, “Festigkeitsprobleme im Maschinenbaum. Encyklopadie der Math,” Wiss. V/4C, Leipzig, 1910, pp. 311-385.
- M. Horn and I. Lasiecka, “Uniform Decay of Weak Solutions to a Von Kármán Plate with Nonlinear Boundary Dissipation,” Differential and Integral Equations, Vol. 7, No. 4, 1994, pp. 885-908.
- M. Horn and I. Lasiecka, “Global Stabilization of a Dynamical Von Kármán Plate with Nonlinear Boundary Feedback,” Applied Mathematics & Optimization, Vol. 31, No. 1, 1995, pp. 57-84. doi:10.1007/BF01182557
- M. Horn, A. Favini, I. Lasiecka and D. Tataru, “Global Existence, Uniqueness and Regularity to a Von Kármán System with Nonlinear Boundary Dissipation,” Differential and Integral Equations, Vol. 9, No. 2, 1996, pp. 267-294.
- G. P. Menzala and E. Zuazua, “Energy Decay Rates for the Von Kármán System of Thermoelastic Plates,” Differential and Integral Equations, Vol. 11, No. 5, 1998, pp. 755-770.
- J. E. M. Rivera and G. P. Menzala, “Decay Rates of Solutions of a Von Kármán System for Viscoelastic Plates with Memory,” Quarterly of Applied Mathematics, Estados Unidos, Vol. 82, No. 1, 1999, pp.181-200.
- J. E. M. Rivera, H. P. Oquendo and M. L. Santos, “Asymptotic Behavior to a Von Kármán Plate with Boundary Memory Conditions,” Nonlinear Analysis, Vol. 62, No. 7, 2005, pp. 1183-1205. doi:10.1016/j.na.2005.04.025
- C. A. Raposo and M. L. Santos, “General Decay to a Von Kármán System with Memory,” Nonlinear Analysis, Vol. 74, No. 3, 2011, pp. 937 - 945. doi:10.1016/j.na.2010.09.047
- G. Avalos and I. Lasiecka, “Uniform Decays in Nonlinear Thermoelastic System,” In: W. Hager and P. Pardalos, Eds., Optimal Control, Theory Algorithms and Application, Kluwer, 1998, pp. 1-23.
- G. Avalos, I. Lasiecka and R. Triggiani, “Uniform Stability of Nonlinear Thermoelastic Plates with Free Boundary Conditions,” International Series of Numerical Mathematics, Vol. 133, 1999, pp. 13-32.
- H. Koch and A. Stahel, “Global Existence of Classical Solutions to the Dynamical Von Kármán Equations,” Mathematical Methods in the Applied Sciences, Vol. 161, 1993, pp. 581-586. doi:10.1002/mma.1670160806
- J. Puel and M. Tucsnak, “Boundary Stabilization for the Von Kármán Equations,” SIAM Journal on Control and Optimization, Vol. 33, No. 1, 1996, pp. 255-273. doi:10.1137/S0363012992228350
- A. Adams, “Sobolev Spaces,” Academic Press, New York, 1975.
- G. P. Menzala, V. Bisognin, E. Bisognin and E. Zuazua, “On Exponential Stability for Von Kármán Equations in the Presence of Thermal Effects,” Mathematical Methods in the Applied Sciences, Vol. 21, No. 5, 1988, pp. 393- 416.
NOTES
*Corresponding author.

