Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20076 , 6 pages DOI:10.4236/am.2012.36078
The Construction Method for Solving Radial Flow Problem through the Homogeneous Reservoir
1Institute of Applied Mathematics, Xihua University, Chengdu, China
2State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, China
Email: *supinf2003@yahoo.com.cn
Received December 9, 2011; revised April 27, 2012; accepted May 5, 2012
Keywords: Differential Equation; Fluid Flow in Porous Media; Boundary Value Problem; Construction Method; Similar Structure; Radial Flow; Homogeneous Reservoir
ABSTRACT
On the basis of similar structure of solutions of ordinary differential equation (ODE) boundary value problem, the similar construction method was put forward by solving problems of fluid flow in porous media through the homogeneous reservoir. It is indicate that the pressure distribution of dimensionless reservoir and bottom hole in Laplace space, which take on the radial flow, also shows similar structure, and the internal relationship between the above solutions were illustrated in detail.
1. Introduction
Due to the permeability of porous media, reservoir engineers could simulate fluid flow by using media such as ground rock, filters and catalyst beds as well, it is useful to those researches who are interested in the behavior of porous media in different engineering applications. Mechanics of porous media flow plays an important role in many branches of engineering, including geotechnical engineering, material science, biomechanics and petroleum industry.
In 2004, S. C. Li [1,2] proposed a important conjecture that the solution formula of some differential equations under different conditions have the similarity, which is similar to that real numbers can be expressed as continued fraction and geometric graphics have certain similarity, we call it the similar structure of solutions. Over the past six years, for some second-order homogeneous ODE [1-14], and some second-order homogeneous linear partial differential equations (PDE) in Laplace space [15-21] as well as some mathematical models of fluids flow in porous media [22-34], the right smart evolution had been obtained on the study of the similar structure of their solutions.
The previous studies are separate, since the similar structure of solutions merely deduced from one certain model of the differential equation boundary value problem, and that was apparently gone against the analysis of the internal relationship between solutions of different models. This paper is intended to reveal the internal relationships between different mathematical models. First of all, in section two, we provide the theoretical background materials of the similar structure of solutions for solving the modified Bessel equation boundary value problem. Secondly, in section tree and four, we devote to solve the problem of fluid flow in porous media through the homogeneous reservoir. At last, in the fifth section, we reveal the inherent laws between above solutions.
2. The Similar Structure of Solutions of the Modified Bessel Equation Boundary Value Problem
In [1] gives the boundary value problem of the modified Bessel equation
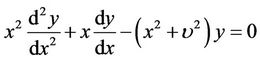 (1)
(1)
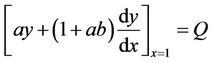 (2)
(2)
 (3a)
(3a)
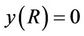 (3b)
(3b)
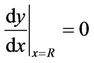 (3c)
(3c)
where a, b,  , R and Q are real constants, and
, R and Q are real constants, and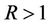 , its solution can be expressed as the following similar structure form
, its solution can be expressed as the following similar structure form
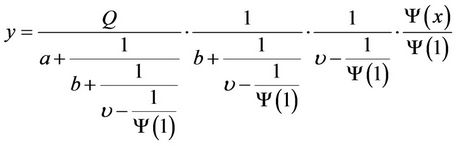 (4)
(4)
where 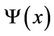 is called the similar kernel function and defined as
is called the similar kernel function and defined as
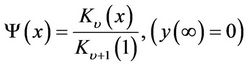 (5)
(5)
 (6)
(6)
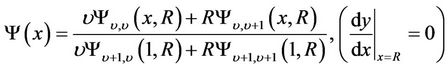 (7)
(7)
where
 ,
,
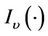 denotes the first kind modified Bessel function with order
denotes the first kind modified Bessel function with order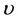 , and
, and  denotes the second kind modified Bessel function with order
denotes the second kind modified Bessel function with order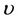 . Furthermore, we have
. Furthermore, we have
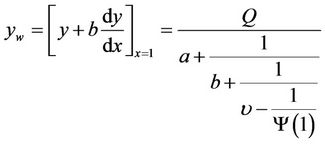 (8)
(8)
When  in the modified Bessel Equation (1), if we setting
in the modified Bessel Equation (1), if we setting 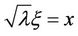 (where
(where  is real constant, and
is real constant, and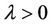 ), then y satisfies the ODE
), then y satisfies the ODE
 (9)
(9)
Similarly as Equations (2) and (3) the boundary value conditions are
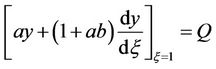 (10)
(10)
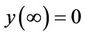 (11a)
(11a)
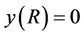 (11b)
(11b)
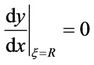 (11c)
(11c)
Quite similar to solve the ODE boundary value problem, by Equations (9) and (11) have the following similar structure form of solution
 (12)
(12)
where 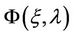 is also called the similar kernel function and defined as
is also called the similar kernel function and defined as
 (13)
(13)
 (14)
(14)
 (15)
(15)
where
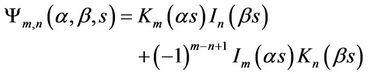 (16)
(16)
In particular, we also have
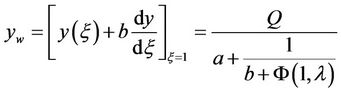 (17)
(17)
3. The Radial Flow Problem through the Homogeneous Reservoir
According to [22], the mathematical model of radial flow through the homogeneous reservoir has been described as follows
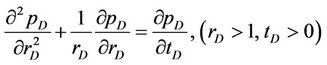 (18)
(18)
 (19)
(19)
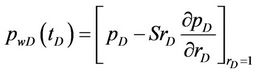 (20)
(20)
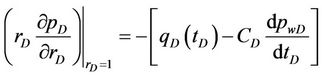 (21)
(21)
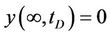 (22a)
(22a)
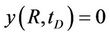 (22b)
(22b)
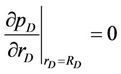 (22c)
(22c)
where pD, rD, tD, CD, RD, and qD are dimensionless variables respectively represent the pressure of any point in reservoir, the distance of reservoir from any point to the wellbore, time, the wellbore storage coefficient, the outer boundary radius of circular reservoir and the liquid flow output of bottom hole (which may depend on time t), and S is the skin factor (well bottom pollution factor). The outer boundary conditions
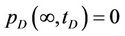 ,
, 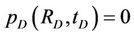
and
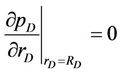
denote that the outer boundary of circular reservoir are infinite, constant pressure and closed respectively.
Taking the Laplace transform of 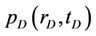 with respect to tD, we obtain the ODE with parameter z (where z is variable in Laplace space)
with respect to tD, we obtain the ODE with parameter z (where z is variable in Laplace space)
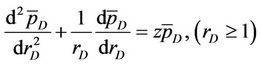 (23)
(23)
and with the boundary conditions
 (24)
(24)
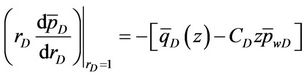 (25)
(25)
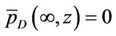 (26a)
(26a)
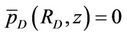 (26b)
(26b)
 (26c)
(26c)
If let
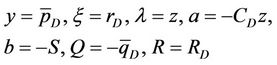 (27)
(27)
then the boundary value problem, Equations (23)-(26) becomes the boundary value problem of Equations (9)- (11). Consequently, according to Equation (12), we know that the similar structure formula of dimensionless reservoir pressure distribution at any point for homogeneous reservoir radial flow model in Laplace space is
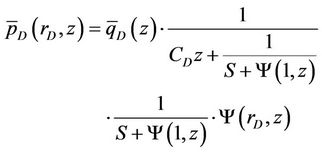 (28)
(28)
where  is called the similar kernel function and defined as
is called the similar kernel function and defined as
 (29)
(29)
 (30)
(30)
 (31)
(31)
Similarly, according to Equation (17), we see that the similar structure formula of dimensionless well bottom hole pressure distribution for homogeneous reservoir radial flow model in Laplace space is
 (32)
(32)
In particular, when the liquid flow output of bottom hole is constant, set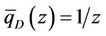 , then Equations (28) and (32) still hold.
, then Equations (28) and (32) still hold.
4. The Radial Flow Problem through the Homogeneous Reservoir Considering the Effective Well Radius
According to [35], the mathematical model of radial flow through the homogeneous reservoir has been described as follows
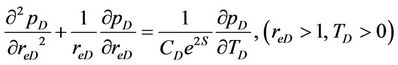 (33)
(33)
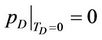 (34)
(34)
 (35)
(35)
 (36a)
(36a)
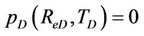 (36b)
(36b)
 (36c)
(36c)
where ,
, 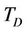 and
and 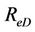 are given as follows, respectively
are given as follows, respectively
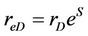 ,
, 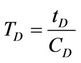 ,
,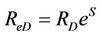 (37)
(37)
The outer boundary conditions
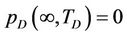 ,
, 
and

denote that the outer boundary of circular reservoir are infinite, constant pressure and closed, respectively.
Taking the Laplace transform of  with respect to
with respect to , we obtain the ODE with parameter z (where z is variable in Laplace space)
, we obtain the ODE with parameter z (where z is variable in Laplace space)
 (38)
(38)
and with the boundary value conditions
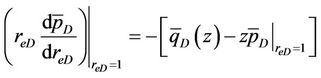 (39)
(39)
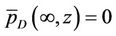 (40a)
(40a)
 (40b)
(40b)
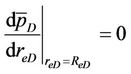 (40c)
(40c)
If let
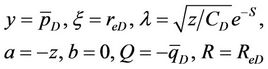 (41)
(41)
then the boundary value problem Equations (38)-(40) becomes the boundary value problem Equations (9)-(11). Consequently, according to Equation (12), we know that the similar structure formula of dimensionless reservoir pressure distribution at any point for homogeneous reservoir radial flow model in Laplace space is
 (42)
(42)
where 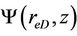 is called the similar kernel function and defined as
is called the similar kernel function and defined as
 (43)
(43)
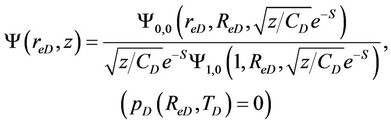 (44)
(44)
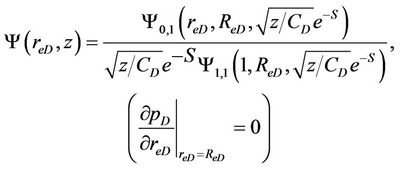 (45)
(45)
Similarly, according to Equation (17), we know that the similar structure formula of dimensionless bottom hole pressure distribution for homogeneous reservoir radial flow model in Laplace space is
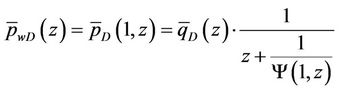 (46)
(46)
In particular, when the liquid flow output of bottom hole is constant, set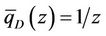 , then Equations (42) and (46) still hold.
, then Equations (42) and (46) still hold.
5. Conclusions
Form above discussion, the conclusion can be reached that 1) In section three and four, we use the property of similar structure of ODE boundary value problem, and in the process of solving problem of radial flow through homogeneous reservoir in Laplace space, we can get the expecting outcome by means of algebra constructive theory in Laplace space, and avoid the procedure of solving Bessel equation and the complicated partial derivative operation, but making simple change of variables (such as Equation (27) or Equation (41)) only.
We find this is a simple, convenient and effective method, and an innovation idea for solving problem of fluid flow in porous media.
2) Different similar kernel functions (see Equations (5)-(7), (13)-(15), (29)-(31) and (43)-(45)) corresponding to different right (outer) boundary value conditions (see Equations (3), (11), (22) and (36)), respectively. Actually, the similar kernel functions are the basic solutions which corresponding to the especial left (inner) boundary value conditions (see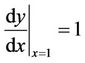 ,
,  ,
, 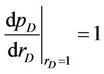 and
and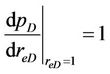 ) respectively.
) respectively.
3) The similar structure formula of solutions (see Equations (4) or (8), (12) or (17), (28) or (32) and (42) or (46)) depend on the left (inner) boundary conditions (see Equations (2), (10), (24), (25) and (39)), instead of the determine equations (see Equations (1), (9), (23) and (38)) and the right (outer) boundary value conditions (see Equations (3), (11), (22) and (36)). From the unified expression in Equation (28) and (32), it is easy to see how the wellbore storage effects, skin factors, as well as the outer boundaries influence the reservoir pressure and bottom hole pressure. This expression brought great convenience for programming well test analysis software, and simplified the program algorithm.
4) If take the Laplace transform to the measured pressure data, well test analysis (dynamic analysis of pressure) can be conducted directly in Laplace space, this also can reflect the advantage of the similar structure of solutions in this paper. In general, using Stehfest numerical inversion formula, the solutions we got in this paper can be transformed into numerical solution in real space, which fully meat the need of the application of well test analysis.
5) This arouses our interest in studying the similar structure of solutions. On the one hand, it is clearly that we can get direct solutions satisfying more especial left (inner) boundary conditions (such as the real constants and in Equation (2) satisfying restricted conditions) from the similar structure expression. On the other hand, using the similar structure expression and the basic solutions (i.e. the similar kernel functions), we can construct some more complicated practical problems. Therefore, we put forward the construction method for solving the boundary value problem of ODE, and it is called the similar construction method.
6. Acknowledgements
This work was supported by the Natural Science Key Projects of the Sichuan Education Bureau of China (No. 12ZA164), the Research Fund of Key Disciplinary of Application Mathematics of Xihua University (No. XZD0910-09-1), and the Graduate Innovation Found of Xihua University (No. YCJJ201110).
REFERENCES
- S. C. Li, L. Z. Yi and P. S. Zheng, “The Similar Structure of Differential Equations on Fixed Solution Problem,” Journal of Sichuan University (Natural Science Edition), Vol. 43, No. 4, 2006, pp. 933-934.
- M. H. Jia and S. C. Li, “The Similar Structure of Solution Differential Equation on Boundary Value Problem,” College Mathematics, Vol. 21, No. 5, 2005, pp. 37-39.
- R. P.Agarwal and D. O’Regan, “Ordinary and Partial Differential Equations,” Springer, New York, 2009.
- D. L. Powers, “Boundary Value Problems,” 5th Edition, Academic Press, Elsevier, New York, 1999.
- M. A. Khamsi, “Homogeneous Linear Equations with Constant Coefficients,” 1992. http://www.sosmath.com/diffeq/second/constantcof/constantcof.html.
- P. S. Zheng, S. C. Li and Y. F. Zhang, “The Formal Similarity of Solutions on the Class of Ordinary Differential Equation System,” Journal of Jilin University (Information Science Edition), Vol. 23, No. 8, 2005, pp. 56-60.
- P. S. Zheng, S. C. Li and Y. F. Zhang, “The Solution’s Structure of a Type of Ordinary Differential Equation System with Closed Right Boundary Conditions,” Journal of Xihua University (Natural Science Edition), Vol. 24, No. 6, 2005, pp. 88-90.
- Z. C. Chen, P. H. Liu and S. C. Li, “The Similar Structure of Composite Bessel Equation on Fixed Solution Problem,” Journal of Chongqing Techno Business University (Natural Science Edition), Vol. 23, No. 1, 2006, pp. 1-4.
- P. H. Liu, Z. C. Chen and S. C. Li, “Similar Structure of Fixed Solution Problems for Composite Abnormal Bessel Equations,”Journal of Xihua University (Natural Science Edition), Vol. 25, No. 2, 2006, pp. 23-26.
- S. C. Li, “The Similar Structure of Solution of Second-Order Linear Homogeneous Differential Equations with Constant Coefficients on the Boundary Value Problem,”Journal of Xihua University (Natural Science Edition), Vol. 26, No. 1, 2007, pp. 84-85.
- S. C. Li, “The Similar Structure of Solution to the Boundary Value Problem for Second-Order Linear Homogeneous Differential Equations,” Journal of Xihua University (Natural Science Edition), Vol. 28, No. 5, 2009, pp. 40-41.
- J. Yan, S. C. Li and C. L. Xing, “The Similar Structures of Solutions to First Class Boundary Value Problem of Second-Order Euler’s Equation,” Journal of Xihua University (Natural Science Edition), Vol. 28, No. 8, 2009, pp. 86-88.
- Q. Y. Li, S. C. Li and Y. Chi, “The Similar Structure of Solution of Linear Homogeneous Differential Equations with Constant Coefficients on the Boundary Value Problem,” Sichuan Ordnance Journal, Vol. 31, No. 4, 2010, pp. 126-129.
- S. C. Li, “Preliminary Exploration and Prospects of the Similar Structure of Solutions of Differential Equations,” Journal of Xihua University (Natural Science Edition), Vol. 29, No. 2, 2010, pp. 223-226.
- J. Kevorkian, “Partial Differential Equations: Analytical Solution Techniques,” 2nd Edition, Springer, New York, 2000.
- A. D. Polyanin, “Handbook of Linear Partial Differential Equations for Engineers and Scientists,” Chapman & Hall/CRC Press, Boca Raton, 2002.
- A. Sommerfeld, “Partial Differential Equations in Physics,” Academic Press, New York, 1949.
- J. D. Tian and S. C. Li, “The Formal Similarity of Solutions in the Laplace Space on the Class of Quasilinear Partial Differential Equation,” Mathematical Theory and Applications, Vol. 24, No. 2, 2004, pp. 66-73.
- M. H. Jia and S. C. Li, “The Formal Similarity of Solutions in the Laplace Space on the Class of Fluid Flow Differential Equation,” Journal of Electronic Science and Technology of China, Vol. 3, No. 2, 2005, pp. 172-174.
- S. C. Li, “The Formal Similarity of Solutions in the Laplace Space on the Class of Partial Differential Equation System,” Journal of Xihua University (Natural Science Edition), Vol. 26, No. 4, 2007, pp. 83-86.
- J. P. Su, S. C. Li and C. J. Li, “The Similar of Solutions in the Laplace Space of Composite Parabolic Partial Differential Equation,” Journal of Zaozhuang University, Vol. 26, No. 2, 2009, pp. 6-11.
- S. C. Li, P. S. Zheng and Y. F. Zhang, “The Similar Structure of Pressure Distribution in the Homogenous Reservoir,” Pure and Applied Mathematics, Vol. 22, No. 4, 2006, pp. 459-463.
- W. Z. Xu, S. C. Li and P. S. Zheng, “The Structure of the Solution of Pressure Distribution in the Fractal Homogenous Reservoir and Analytic Graph,” Mathematics and its Applications, Atomic Energy Publishing Company, Beijing, 2007, pp. 541-544.
- S. C. Li, P. S. Zheng and Y. F. Zhang, “The Similar Structure of Pressure Distribution in the Composite Reservoir,” Journal of Mathematics in Practice and Theory, Vol. 38, No. 3, 2008, pp. 23-28.
- S. C. Li, P. S. Zheng and Y. F. Zhang, “Similar Structure of Pressure Distribution in the Multilayer Reservoir,” Applied Mathematics A Journal of Chinese Universities, Vol. 24, No. 2, 2009, pp. 234-238.
- S. C. Li, X. P. Li and B. G. Huang, “Research on Homogeneous Reservoir Pressure Performance,” Drilling & Production Technology, Vol. 25, No. 1, 2002, pp. 50-51.
- S. C. Li, D. H. Liu and P. Z. Zhang, “Pressure Distribution of the Homogeneous Reservoir with Different Boundary Conditions,” Journal of Jianghan Petroleum Institute, Vol. 23, No. 2, 2001, pp. 16-17.
- S. C. Li, P. S. Zheng and Y. F. Zhang, “The Similar Structure of Pressure Distribution in the Fractal Reservoir,” Resources, Environment & Porous Flow Mechanics, Proceedings of 8th Research Conference of Porous Flow Mechanics of China, China Scientific & Technical Publishers, Beijing, 2005, pp. 79-83.
- S. C. Li and J. J. Zhang, “Similar Structure of Pressure Distribution in the Fractal Dual Porosity Reservoir,” Journal of Xihua University (Natural Science Edition), Vol. 25, No. 1, 2006, pp. 40-43.
- C. X. Xu, S. C. Li and W. B. Zhu, “The Similar Structure of Pressure Distribution in the Dual Porosity Reservoir,” Drilling & Production Technology, Vol. 29, No. 4, 2006, pp. 28-30.
- C. X. Xu, S. C. Li and W. B. Zhu, “The Similar Structure of Pressure Distribution in the Fractal Composite Reservoir,” Drilling & Production Technology, Vol. 29, No. 5, 2006, pp. 39-42.
- P. S. Zheng, C. X. Xu and W. Z. Xu, “Well Analusis Method Based on the Similar Structure of Pressure Distribution in the Composite Reservior,” Drilling & Production Technology, Vol. 30, No. 3, 2007, pp. 49-50.
- W. B. Zhu, S. C. Li and C. X. Xu, “The Similar Structure of Pressure Distribution in the Fractal Multilayer Reservoir,” Drilling & Production Technology, Vol. 31, No. 3, 2008, pp. 67-69.
- P. S. Zheng, S. C. Li and W. B. Zhu, “The Similar Structure of Pressure Distribution in the Double Porosity Composite Reservoir,” Drilling & Production Technology, Vol. 31, No. 4, 2008, pp. 80-81.
- S. C. Li and B. G. Huang, “Laplace Transform and Bessel Functions and the Theoretical Basis of Well Test Analysis,” Petroleum Industry Press, Beijing, 2000.
NOTES
*Corresponding author.

