Applied Mathematics
Vol.3 No.1(2012), Article ID:16756,5 pages DOI:10.4236/am.2012.31003
A Note on Stability of Longitudinal Vibrations of an Inhomogeneous Beam
1Department of Mathematics, National Institutes of Technology, Durgapur, India
2Department of Mathematics, J. K. College, Purulia, India
Email: {pknandi.math, goraing}@gmail.com
Received September 18, 2011; revised November 28, 2011; accepted December 5, 2011
Keywords: Inhomogeneous beam; longitudinal vibrations; uniform stabilization; energy decay estimate
ABSTRACT
In this paper, we have considered an inhomogeneous beam with a damping distributed along the length of the beam. The beam is clamped at both ends and is assumed to vibrate longitudinally. We have estimated the total energy of the system at any time t. By constructing suitable Lyapunov functional, it is established directly that the energy of this system decays exponentially.
1. Introduction
In the last few decades the use of flexible structures is on rise. Research in the area of stabilization of vibrations of flexible structures like strings, beams, plates has been gaining importance since early seventies. The study of the stabilization for these problems is significant in the sense to suppress the vibrations to assure a good performance of the overall system.
The vibrations of flexible structures are usually nonlinear in practice. As the non-linear study of such structures is rather cumbersome for analytical treatment, so linearized mathematical models are chosen for simplicity and concise results. The linearized vibrations of flexible structures are usually governed by partial differential equations, particularly, the second order wave equation and the fourth-order Euler-Bernoulli beam equation. Several authors have established stabilization for the wave equation in a bounded domain (cf. G. Chen [1,2], J. Lagnese [3,4], J. L. Lions [5], V. Komornik [6] and the references therein). There are different types of stability for the vibrations of flexible structures and the most important of all these is the uniform stability. Recently, P. K. Nandi, G. C. Gorain and S. Kar [7] has established the uniform exponential stabilization of a solar panel for flexural modes of vibrations. The exponential energy decay estimate is established by Yaojun Ye [8] in case of nonlinear Kirchoff-type vibrations.
The energy decay estimate in developing the theory of stabilization over distributed parameter system in view of its application in various flexible structures has been established by several authors (cf. G. Chen [1,2], J. Lagnese [3,4], J. L. Lions [5], V. Komornik and E. Zuazua [9]). The question of uniform stabilization or point-wise stabilization of Euler-Bernoulli beams or serially connected beams has been studied by a number of authors (cf. J. L. Lions [5], K. Ammari and M. Tuesnak [10], K. Liu and Z. Liu [11], K. Nagaya [12], R. Rebarbery [13] etc.).
2. Mathematical Formulation of the Problem
We consider a flexible inhomogeneous beam of length ![]() which is clamped at both ends. It is initially set to vibrate in the longitudinal direction along
which is clamped at both ends. It is initially set to vibrate in the longitudinal direction along 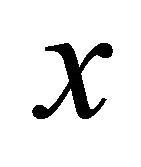 axis. At time
axis. At time , if
, if 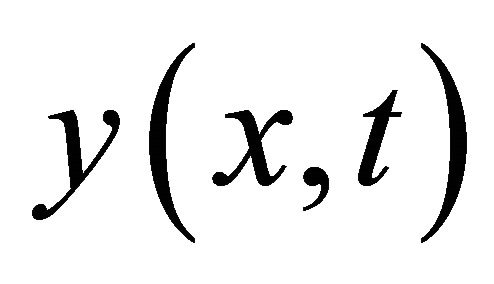 is the longitudinal displacement of the beam at a position
is the longitudinal displacement of the beam at a position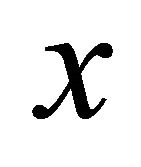 , then it satisfies the differential equation (cf. K. Liu and Z. Liu [11])
, then it satisfies the differential equation (cf. K. Liu and Z. Liu [11])
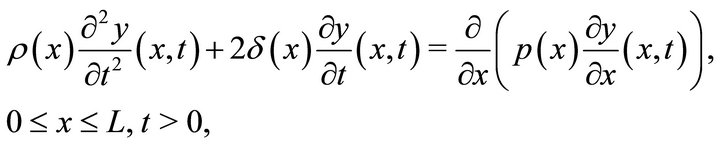 (1)
(1)
where the coefficients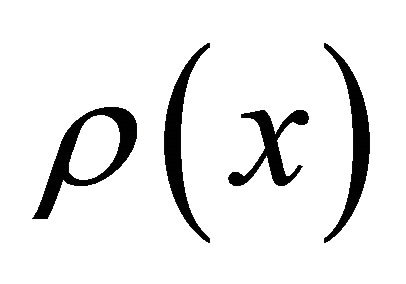 ,
, 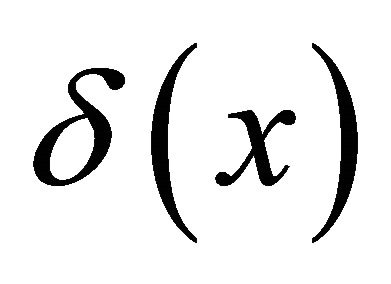 and
and 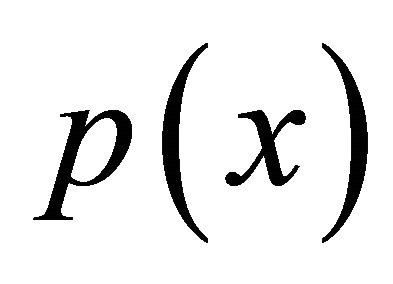 are functions of
are functions of ![]() for a general inhomogeneous beam with
for a general inhomogeneous beam with 
For a clamped beam, the boundary conditions are
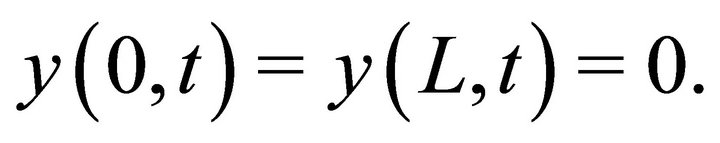 (2)
(2)
Let the beam be set to vibrate with initial values
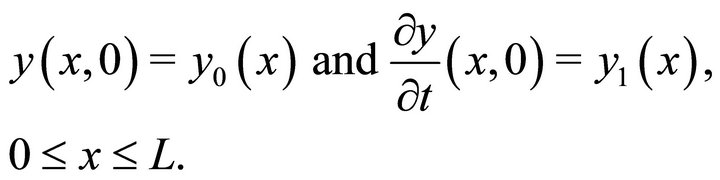 (3)
(3)
3. Energy of the System
The total energy E(t) of the System (1)-(3) at time t is defined by
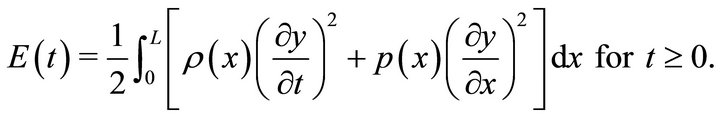 (4)
(4)
Differentiating (4) with respect to t and using (1), we obtain
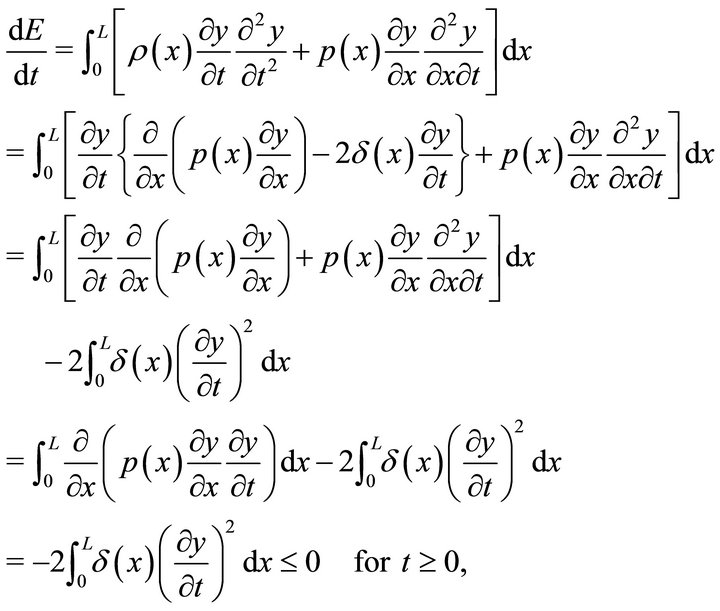 (5)
(5)
where the integration is performed by parts and the boundary conditions in (2) are used. Integrating (5) over [0, t], we get
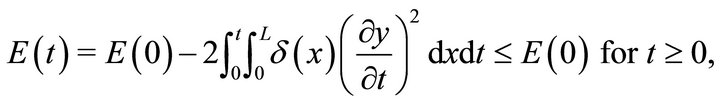 (6)
(6)
where
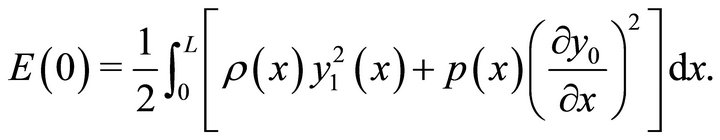 (7)
(7)
In view of (5), the rate of change of energy with time is negative, so the energy of the system is dissipating with time. Our aim in this work is to establish the uniform exponential decay of this energy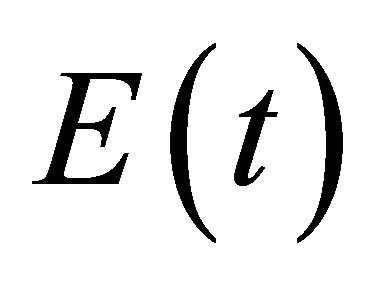 .
.
Now the estimate (6) implies that, if 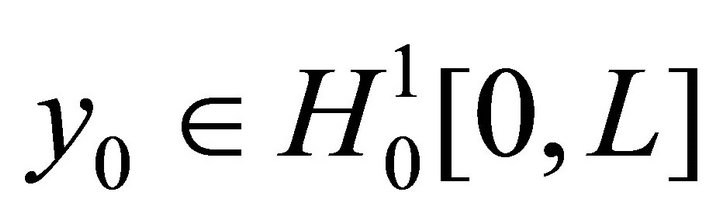 and
and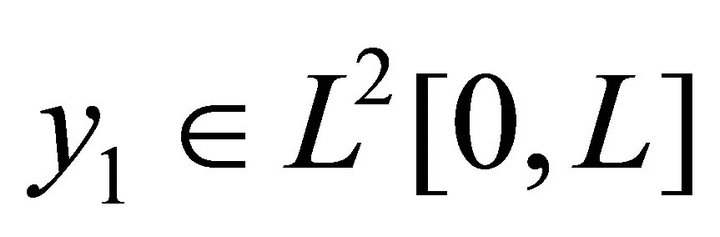 , where
, where
 (8)
(8)
is the subspace of the classical Sobolev space
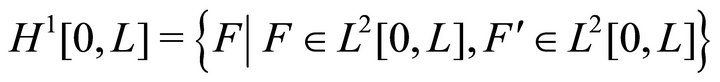 (9)
(9)
of real valued functions of order one, then 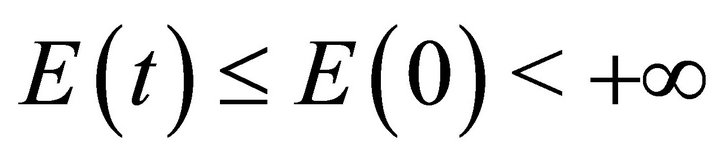 for every
for every 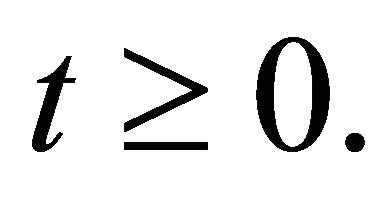 Hence the System (1)-(3) has a unique solution for
Hence the System (1)-(3) has a unique solution for 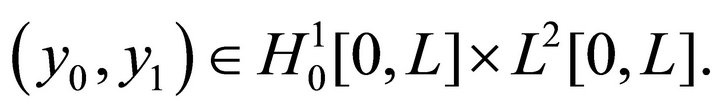
4. Uniform Stability Result and Proof
The main result of this paper can be stated in the following theorem.
Theorem 1. Let 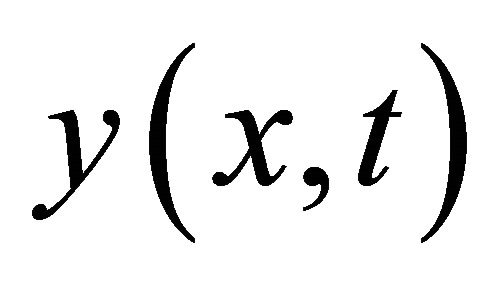 be a solution of the system (1)-(3) with the initial values
be a solution of the system (1)-(3) with the initial values 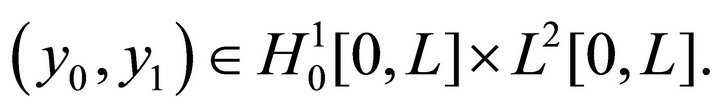 Then the total energy of the system decays uniformly exponentially with time, that means, the energy
Then the total energy of the system decays uniformly exponentially with time, that means, the energy 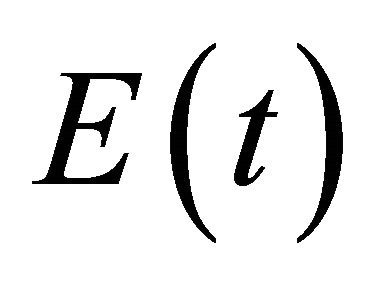 satisfies the relation
satisfies the relation
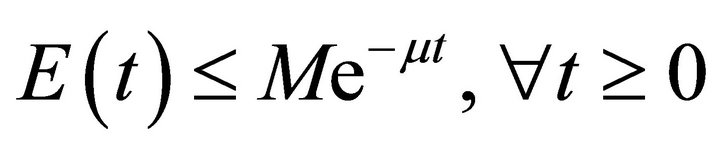 (10)
(10)
for some finite reals 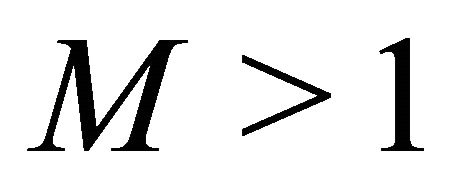 and
and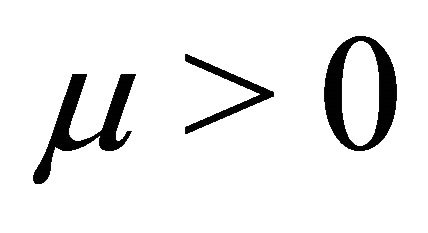 , both being independent of time
, both being independent of time .
.
The theorem will be proved using the following results. For any real number 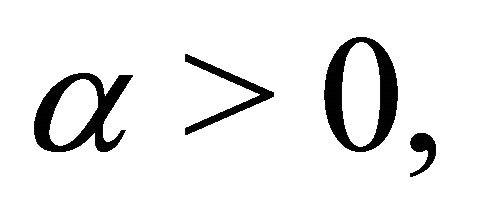 we have by the CauchySchwartz’s inequality
we have by the CauchySchwartz’s inequality
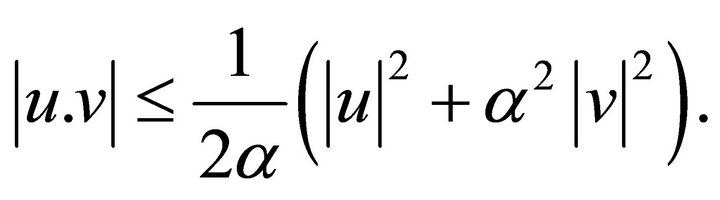 (11)
(11)
By Poincare type Scheeffer’s inequality [14], we have
 (12)
(12)
By mean value theorem of integral calculus, there are reals ,
,  ,
,  ,
, 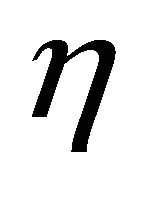 ,
,  satisfying
satisfying
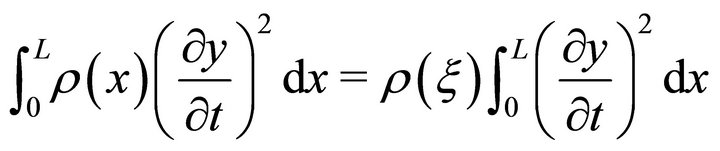 (13)
(13)
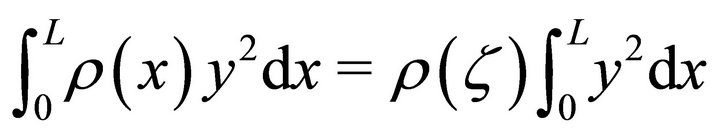 (14)
(14)
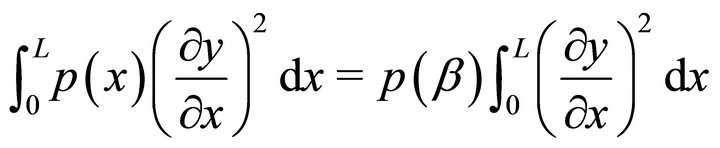 (15)
(15)
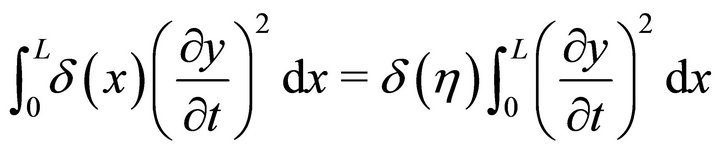 (16)
(16)
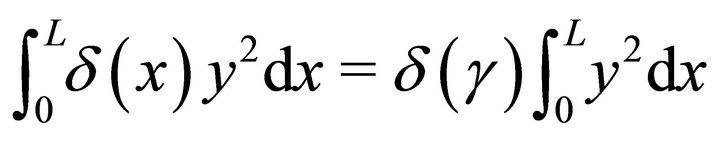 (17)
(17)
Next we consider the following lemmas:
Lemma 1. For every solution 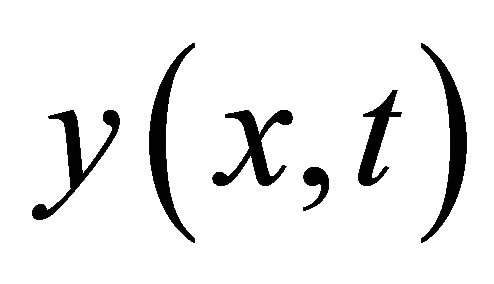 of the system (1)-(3), the time derivative of the functional
of the system (1)-(3), the time derivative of the functional  (cf. G. C. Gorain [15], G. C. Gorain and S. K. Bose [16]) defined by
(cf. G. C. Gorain [15], G. C. Gorain and S. K. Bose [16]) defined by
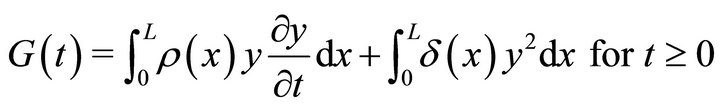 (18)
(18)
satisfies
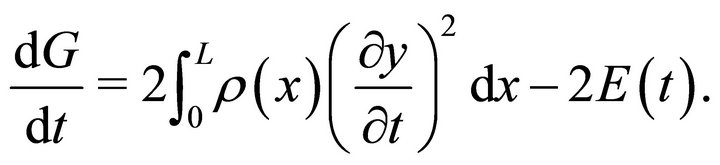 (19)
(19)
Proof: Differentiating (18) with respect to  and using the equation (1), we obtain
and using the equation (1), we obtain
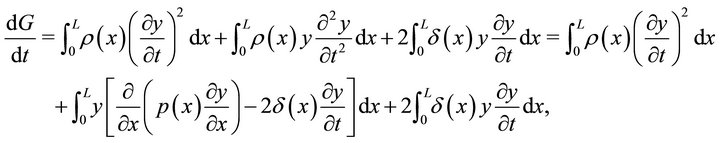 (20)
(20)
Integrating by parts and using the boundary Conditions (2) and the energy Identity (4), we get
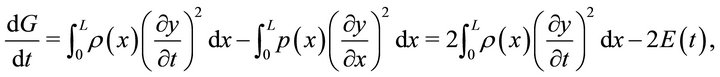 (21)
(21)
Hence the lemma.
Lemma 2. For every solution  of the System (1)-(3), an estimate of the functional
of the System (1)-(3), an estimate of the functional  is given by
is given by
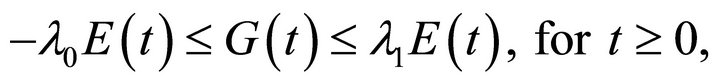 (22)
(22)
where
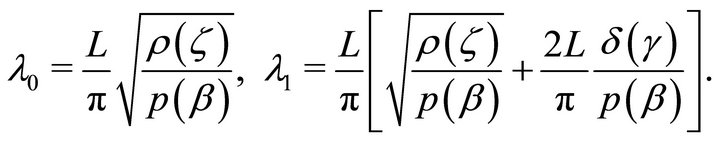 (23)
(23)
Proof: We can estimate the 1st term (18) as,
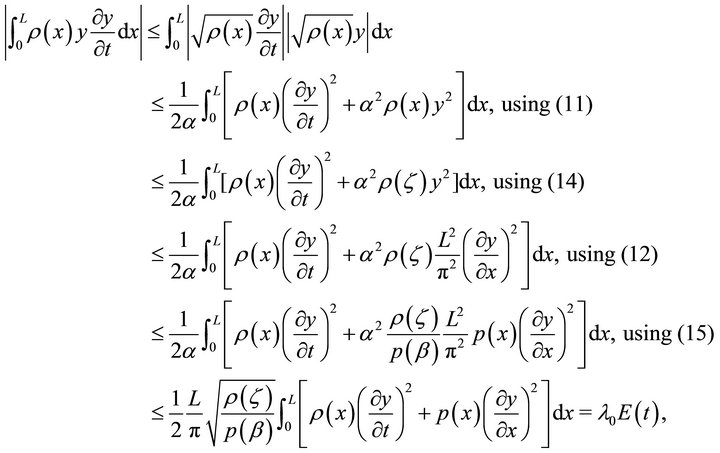 (24)
(24)
where
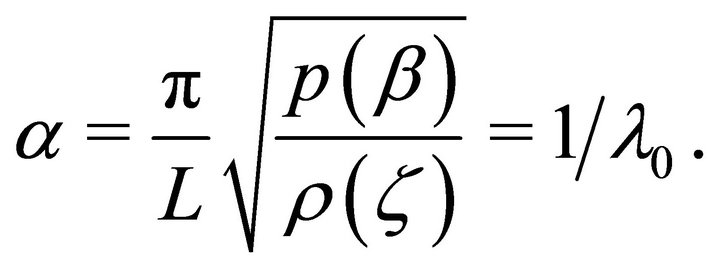 (25)
(25)
Again, we can estimate the 2nd term (18) as,
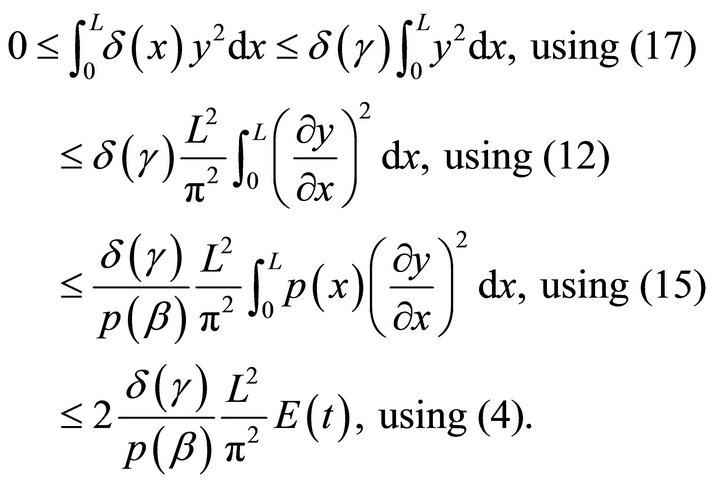 (26)
(26)
Adding (24) and (26), the lemma follows immediately.
Proof of Theorem 1: Proceeding as in G. C. Gorain [15] and G. C. Gorain and S. K. Bose [16], we define energy like Lyapunov functional 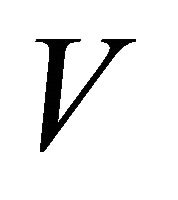 by
by
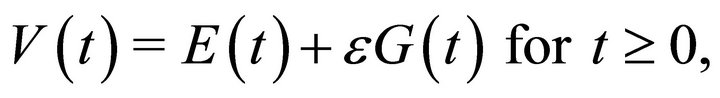 (27)
(27)
where 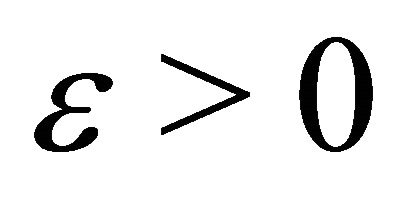 is a small constant.
is a small constant.
In view of Lemma 2, the functional 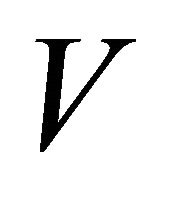 defined by (27) can be estimated as
defined by (27) can be estimated as
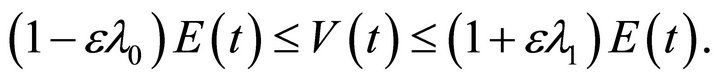 (28)
(28)
Since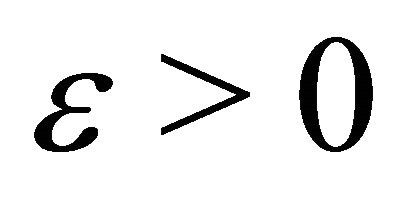 , we may assume that
, we may assume that
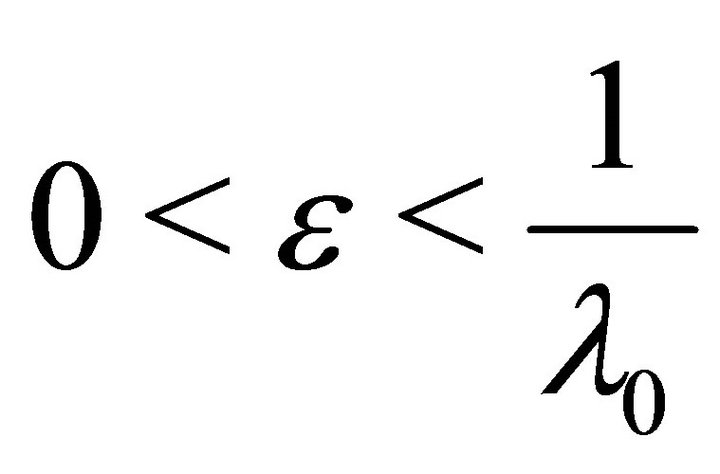 (29)
(29)
so that 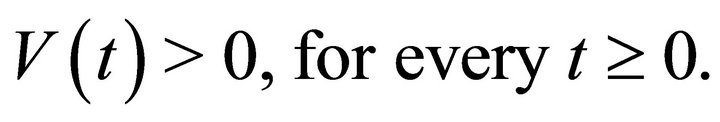
Differentiating (27) with respect to , and using (5) and (19), we obtain
, and using (5) and (19), we obtain
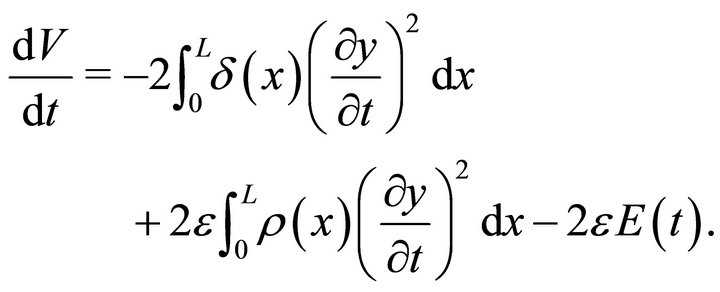 (30)
(30)
Hence, using the above relation (13) and (16), we can write (30) as
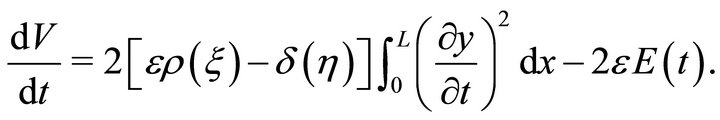 (31)
(31)
Since 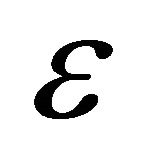 is small, we may choose further
is small, we may choose further
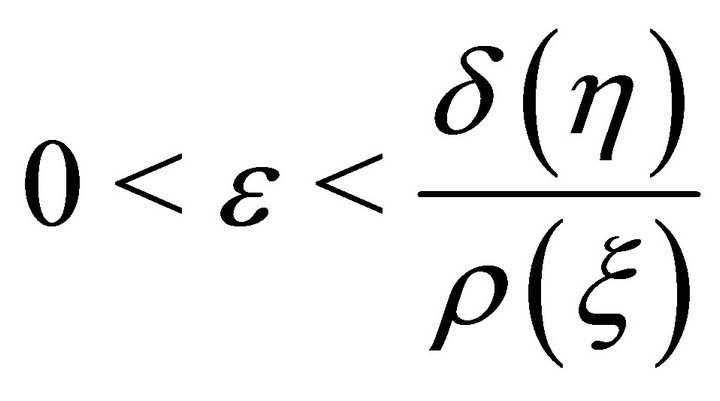 (32)
(32)
so that the differential relation (31) reduces to
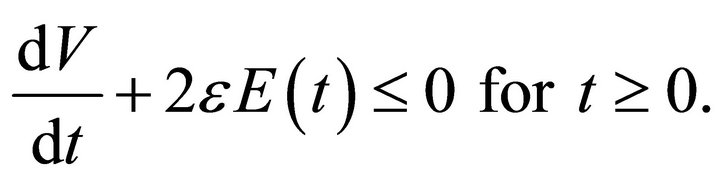 (33)
(33)
Invoking the Inequality (28), the relation (33) leads to the differential inequality
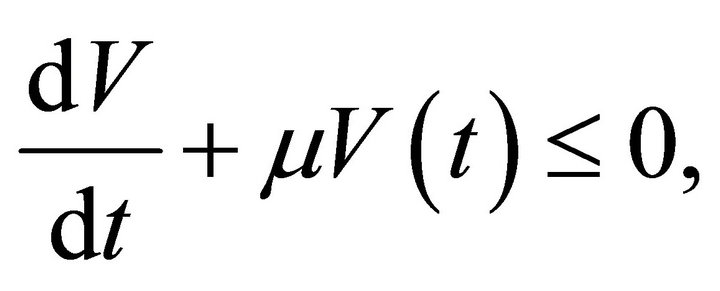 (34)
(34)
where
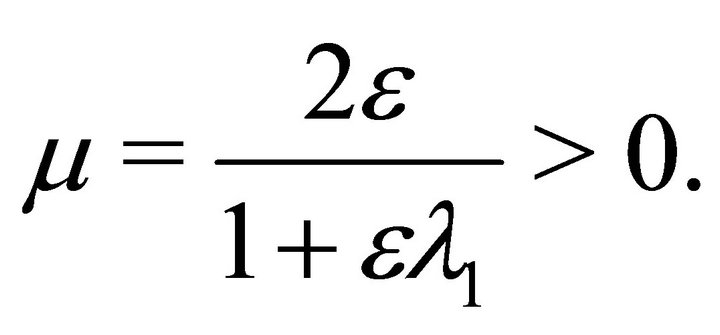 (35)
(35)
Multiplying (34) by 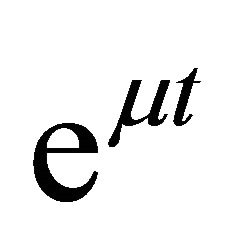 and integrating from 0 to
and integrating from 0 to , we obtain
, we obtain
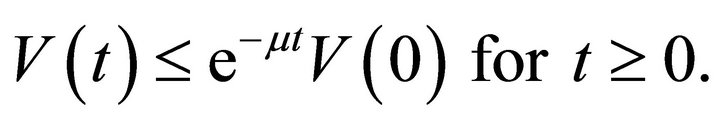 (36)
(36)
Applying again the inequality (28) in (36), we get
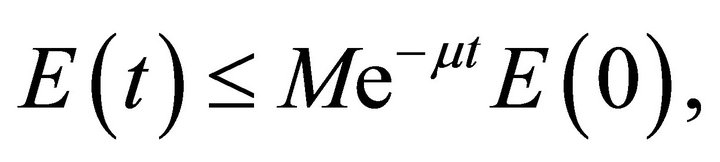 (37)
(37)
where
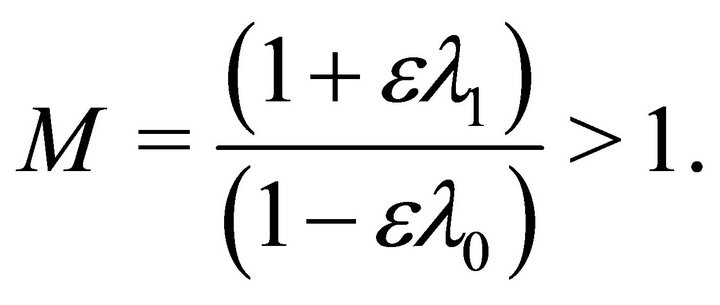 (38)
(38)
Hence the theorem.
5. Conclusion
We have established here the uniform stabilization of the vibrations of an inhomogeneous beam which is clamped at both ends. The result is achieved directly by means of an exponential energy decay estimate. It is significant in the sense that the solution of the system given by (1)-(3) converges uniformly to zero as time  tends to
tends to . The result shows that the vibrations of the inhomogeneous beam decay rapidly for large value of
. The result shows that the vibrations of the inhomogeneous beam decay rapidly for large value of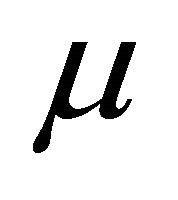 . Again
. Again
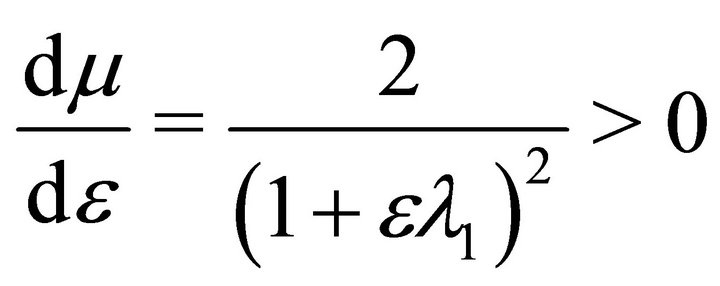 (39)
(39)
shows that exponential decay rate being a function of 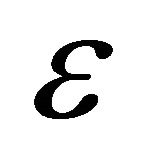 will be maximum for largest admissible value of
will be maximum for largest admissible value of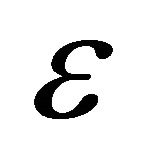 .
.
REFERENCES
- G. Chen, “Energy decay estimates and exact boundaryvalue controllability for the wave equation in a bounded domain,” Journal de Mathématiques Pures et Appliquées, Vol. 58, 1979, pp. 249-273.
- G. Chen, “A note on the boundary stabilization of the wave equation,” SIAM Journal of Control and Optimization, Vol. 19, No. 1, 1981, pp. 106-113. doi:10.1137/0319008
- J. Lagnese, “Note on boundary stabilization of wave equations,” SIAM Journal of Control and Optimization, Vol. 26, No. 5, 1988, pp. 1250-1256. doi:10.1137/0326068
- J. Lagnese, “Decay of solutions of wave equations in a bounded region with boundary dissipation,” Journal of Differential Equations, Vol. 50, No. 2, 1983, pp. 163-182. doi:10.1016/0022-0396(83)90073-6
- J. L. Lions, “Exact controllability, stabilization and perturbations for distributed systems,” SIAM Review, Vol. 30, No. 1, 1988, pp. 1-68. doi:10.1137/1030001
- V. Komornik, “Rapid boundary stabilization of wave equations,” SIAM Journal of Control and Optimization, Vol. 29, No. 1, 1991, pp. 197-208. doi:10.1137/0329011
- P. K. Nandi, G. C. Gorain and S. Kar, “Uniform exponential stabilization for flexural vibrations of a solar panel,” Applied Mathematics, Vol. 2, No. 6, 2011, pp. 661- 665. doi:10.4236/am.2011.26087
- Y. J. Ye, “On the Exponential Decay of Solutions for Some Kirchoff-Type Modelling Equations with Strong Dissipation,” Applied Mathematics, Vol. 1, No. 6, 2010, pp. 529- 533. doi:10.4236/am.2010.16070
- V. Komornik and E. Zuazua, “A direct method for boundary stabilization of the wave equation,” Journal de Mathématiques Pures et Appliquées, Vol. 69, No. 1, 1990, pp. 33-54.
- K. Ammari and M. Tuesnak, “Stabilization of Bernoulli-Euler Beams by Means of a Point FEedback Force,” SIAM Journal of Control and Optimization, Vol. 39, No. 4, 2000, pp. 1160-1181. doi:10.1137/S0363012998349315
- K. Liu and Z. Liu, “Exponential Decay of Energy of the Euler-Bernoulli Beam with Locally Distributed KelvinVoigt Damping,” SIAM Journal of Control and Optimization, Vol. 36, No. 4, 1998, pp. 1086-1098. doi:10.1137/S0363012996310703
- K. Nagaya, “Method of control of flexible beams subject to forced vibrations by use of inertia force cancellations,” Journal of Sound and Vibration, Vol. 184, No. 2, 1995, pp. 184-194. doi:10.1006/jsvi.1995.0311
- R. Rebarbery, “Exponential stability of Coupled beams with dissipative joints: A frequency domain approach,” SIAM Journal of Control and Optimization, Vol. 33, No. 1, 1995, pp. 1-28. doi:10.1137/S0363012992240321
- D. S. Mitrinović, J. E. Pečarić and A. M. Fink, “Inequalities Involving Functions and Their Integrals and Derivatives,” Kluwer, Dordrecht, 1991.
- G. C. Gorain, “Exponential energy decay estimate for the solutions of n-dimensional Kirchhoff type wave equation,” Applied Mathematics and Computation, Vol. 177, No. 1, 2006, pp. 235-242. doi:10.1016/j.amc.2005.11.003
- G. C. Gorain and S. K. Bose, “Exact controllability and boundary stabilization of torsional vibrations of an internally damped flexible space structures,” Journal of Optimization Theory and Applications, Vol. 99, No. 2, 1998, pp. 423-442. doi:10.1023/A:1021778428222

