Received 24 August 2014; revised 7 October 2014; accepted 1 November 2014

ABSTRACT

In this paper we consider sequences of observations that irregularly space at infrequent time intervals. We will discuss about one of the most important issues of stochastic processes, named Markov chains. We would reconstruct the collected imperfect data as a Markov chain and obtain an algorithm for finding maximum likelihood estimate of transition matrix. This approach is known as 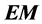algorithm, which includes main optimum advantages among other approaches, and consists of two phases: phase (maximization of target function). Continue the phase 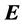and 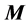to achieve the sequence convergence of matrix. Its limit is the optimal estimator. This algorithm, in contrast with other optimum algorithms which could be used for this purpose, is practicable in maximum likelihood estimate, and unlike to the methods which involve mathematical, is executable by computer. At the end we will survey the theoretical outcomes with numerical computation by using software.

Keywords:

Markov Chain, Matrix Transition, Maximum Likelihood, 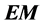Algorithm, Missing Data

1. Introduction

Today, we humans are faced with many of the random variables and processes. One of the most important issues is the random process of Markov chain. Markov chain is often used to describe how the system changes over time. If we are able to model the system sufficiently to form a Markov chain model, we can then evaluate its various theoretical results through system analysis. In this article, the Matrix transition of Markov chain needed for imperfect observation within a given time is obtained through 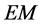algorithm.

The 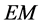algorithm has two stages: 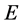stage and 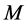stage. This algorithm basically works in this way: We first take into consideration the initial value for the parameter which in this case is the transition matrix.

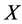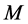The full set of data () is then reconstructed from missing data by estimation of these parameters in stage. In the stage, the maximum likelihood of reconstructed data is maximized to get a new estimation of the parameter. Then, based on this new estimation, the 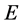stage is repeated and we get the second estimation in the stage. Finally, we continue this process as far as to get convergence estimates.

Dempstr [1] , Raj [2] , Johnson et al. [3] have obtained the value of maximum likelihood of the transition matrix for a sequence of observations.

Among the researchers who examined the issues of statistical inference of Markov chains and published articles in this area are Melichson [4] , Capee [5] , Chip [6] and Robert [7] .

2. Modeling of Missing Data Based on Markov Chain

Following observations in Table 1 are series of real data obtained about a kind of disease related to 3 patients at different times during 6 months in a hospital. We have missed some of the data because the patients have not attended the hospital in some cases. Number 1 indicates that the patient’s condition is satisfactory and number 2 shows the patients are in a very bad condition. The asterisk indicates that in a particular time point, the data has not been observed.

First, the patient’s condition is reported as: 1) Next month, no data are is available. Two months later the condition of that patient is reported as; 2) One month later his condition is reported as (1) again, and so on. We call such a set of data incomplete and it is shown as.

The incomplete data are collected against complete data (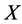) which are gathered in all intervals between the first and the last observation.

Such a system can be modeled as a Markov chain with condition space and transition matrix P.

Generally, we will have if we consider as the number of condition change from to at the time interval. as the transition probability from to condition at t time, as the number of condition change from to in a time unit for the whole data , and as the element of matrix, i.e. condition change probability a stage from to condition. Having this fact in mind that with the incomplete data and the nonzero suitable initial transition matrix, there will be different complete data with their own probabilities, we estimate the transition matrix by the algorithm as follows:

1—First, we change the specified incomplete data () to complete data () by considering a suitable amount for those intervals we have no observation and data. In other words, we reconstruct the complete data () from the incomplete data.

2—We consider an initial value for an arbitrary non-zero element of the transfer matrix as.

3—We compute maximum likelihood of observations with the initial transmission matrix as follows:

(1)

4—We calculate the relative maximum (1) and show it as.

5—We repeat the steps 3 and 4 so much that the obtained matrix sequence gets to convergence matrix, in other words, our optimal estimate is.

The calculation and unique maximum are stated through the following theorem.

Theorem 1: Suppose that the matrix transition of the imperfect data in Table 1 is, then

Proof: We assume the system at the time is in the condition and at the next time interval it is in the condition. The probability that a change occurs between conditions and is done in the time interval is computed according to the Figure 1 provided that the system gets to n condition at from the starting point condition at.

First the system starting from m condition changes to condition with the probability of at the time unit of. Then the system is likely to change to n condition at with the probability of.

Suppose that we define and as follows:

: Cases in which changes from i to j condition occurs at.

: Cases in which system starting from m condition at gets to n condition at.

Then we have:

It is clear that the probability of the number of condition changes between the and conditions along with a change from to condition at the t time interval is equal to:.

So, the expected number of such condition changes in all time intervals is: because and conditions repeatedly occurs at t intervals. Therefore, the expected number of transitions from to condition on the condition of observed data and Matrix transition accumulating on all observed data is obtained as follows:.

Theorem 2: Suppose that the matrix transition of the imperfect data in Table 1 is, then there is a unique relative maximum with its entry is as follows:

Proof:

(2)

Equation (2) has been obtained because the sum of entries in each line is one.

(3)

Adding Equation (3) on, we have:

(4)

By replacing Equation (4) in Equation (3), the proof is completed.

Remark: the fourth stage in algorithm is computed and algorithm is completed as the following:

1) We compute.

2) We compute matrix transition of first stage through this formula:

The obtained s for all and forms another matrix in the form of for the next iteration.

3. Numerical Computation

In this section, all the theories mentioned are surveyed on the Table 1 through a program written in software.

For actual observations we have Table 2 which is number of change from to at the time interval.

Conducting computer program written on the bases of the algorithm to estimate the matrix transition of the system and the original transition, we will have the following outputs:

, ,

, ,

, ,

, ,

,

(5)

Algorithm with another initial matrix will be:

, ,

, ,

, ,

, ,

,

(6)

As it is seen, the results (5) and (6) are the same in either way.

4. Conclusions

In using the algorithm, we are practically faced with some issues which should be focused to accelerate our work and save time.

1) If the initial transition matrix, which is arbitrarily chosen, is of a zero entry or the number of transitions from one condition to another one is zero in a unit of time, the corresponding entries of all produced matrices are zero, too. The initial matrix entries must be non-zero to avoid such condition.

2) Increase in the number of time units between successive observations increases the power of transition matrix. If the number of the observed condition changes is relatively low, the time interval between observations is high. Accordingly, with respect to time needed for computation, it is not economical to integrate all these to-

gether in the analysis. Actually it is better to keep the maximum time interval at the level in which the probability of condition change is ignored. If the maximum time interval is too large, the increase in the time unit can be effective.

3) If the maximum time intervals are relatively low, the computation time of each stage is short, although different performances may be necessary before achieving convergence.

4) In practical computation, we have accepted that when the maximum difference between successive entries of transition matrix is smaller than a predetermined value, e.g.. In other words, convergence is achieved when for all values of i, j, and the given value for r, we have:.

Acknowledgements

The support of Research Committee of Persian Gulf University is greatly acknowledged.

References

NOTES

^*Corresponding author.