Modern Economy
Vol.06 No.02(2015), Article ID:53788,11 pages
10.4236/me.2015.62013

Stock Selection and Timing Ability of the Taiwan Equity Funds―The Application of Stochastic Beta, GARCH, and Nonlinear GLS

Yeong-Jia Goo1, Feng-Huei Chang2*, Kuo-Liang Chiu3

1Department of Business Administration, National Taipei University, Taipei, Taiwan

2Department of Finance, Chihlee Institute of Technology, New Taipei, Taiwan

3Department of Integrated Marketing, Cathay Life Insurance Co., Ltd., Taipei, Taiwan

Email: goo@mail.ntpu.edu.tw, *fenghuei@mail.chihlee.edu.tw, chiu741216@hotmail.com

Copyright © 2015 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 9 January 2015; accepted 28 January 2015; published 4 February 2015

ABSTRACT

This study simultaneously examines funds’ selectivity, beta stationary, and timing decisions by the modified method of Chen and Stockum (1986). We adopt GARCH, generalized least square (GLS), and a nonlinear parameter-estimator model to increase the estimate efficiency. The results indicate that up to 86% of the funds have stochastic betas, over 99% show positive but insignificant selectivity, and 83% indicate negatively significant market-timing ability. This suggests that Taiwan domestic-equity fund managers, on average, do not have stock selectivity and timing ability, which seems to support the efficient market hypothesis.

Keywords:

Mutual Fund, Stock Selectivity, Timing Ability, GARCH, Nonlinear GLS

1. Introduction

The performance evaluation of mutual funds has drawn considerable attention in the finance literature and practice. The basis of conventional fund-performance measurements of market timing was shown to be unrealistic, limiting the manager to constant beta during up and down markets [1] -[3] . Quite a few existing studies presented empirical results that supported an unstable level of systematic risk for mutual funds, such as Klemkosy and Maness [4] , Kon and Jen [5] , Fabozzi and Francis [6] [7] , Miller and Gressis [8] , Radcliffe, Brooks, and Levy [9] , Golec [10] , Busse [11] and Matallín and Fernández-Izquierdo [12] . However, previous related work on the Taiwan fund market is sparse.

Theoretically, the risk that a mutual fund manager faces involves systematic risk (the market risk) and non- systematic risk (the idiosyncratic risk). A fund manager should be capable of minimizing the non-systematic risk by a diversified portfolio. Systematic risk is the main risk, especially in such a globalized financial market where international financial markets correlate closely to each other and when a particular country risk has become the decisive factor that shakes the market prices. For a fund that is designed to be managed by an active strategy, its systematic risk, beta, should vary with the fund manager’s decision-making. In this context, are the systematic risks, betas, of Taiwan mutual funds constant or random? Although much work on the performance evaluation of Taiwan mutual funds has been conducted, so far it has not been clearly understood whether the fund’s systematic risk level is nonstationary. Therefore, the first aim of this study is to examine whether there exists nonstationary beta in Taiwan fund market.

The question of whether professional portfolio managers can deliver expected returns in excess of naive benchmarks has received considerable attention in both academic research and practical decision-making. Fama [13] first made the distinction between stock selection (micro-forecasting) and timing ability (macro-forecasting) as a criterion of mutual fund performance. However, the evidence on the ability of managers to deliver superior stock selection and market timing remains controversial. Kon [14] found that individual funds exhibited positive-timing ability and performance by examining 37 US funds from 1960 to 1976, but concluded that the study results were consistent with the efficient markets hypothesis (EMH). In other words, fund managers as a group did not have special information regarding unanticipated market movements. A large number of previous studies on US mutual funds have reported that a negative relationship is found between a manager’s stock selectivity and market-timing ability. Such studies include Lehman and Modest [15] , Grinblatt and Titman [16] , Cumby and Glen [17] , Connor and Korajczyk [18] , Coggin, Fabozzi, and Rahman [19] , Coggin and Hunter [20] , and Dellva, DeMaskey and Smith [21] . Henriksson [22] used both the Henriksson and Merton parametric and non-parametric models to investigate 116 mutual funds from 1968 to 1980. Only three funds had significantly positive estimates of market-timing ability in the parametric tests for the sample period. Chang and Lewellen (1984) [23] reported that neither skillful market timing nor clever security-selection abilities were evident in abundance in observed mutual fund-return data. Kao, Cheng, and Chan [24] reported that managers of international mutual funds possessed good selectivity and overall performance; however, they also found weak evidence of poor market-timing ability. Grinblatt and Titman [16] [25] and Wermers [26] concluded that mutual fund managers, especially those that oversaw growth-oriented funds, had the ability to choose stocks that outperformed their benchmarks before any expenses were deducted. Wermers [27] found that mutual funds, on average, held stocks that outperformed a broad market index by 130 basis points per year. There seems to be less debate for the examination of positive results on the stock selectivity. However, even with the availability of many measuring models, the empirical results have been quite mixed for market-timing ability. Lee and Rahman [28] found that 16 out of 93 US funds exhibited significant positive-timing ability. Bollen and Busse [29] also showed that mutual funds possessed significant timing ability by examining the daily US fund data.

Related studies on non-US markets are relatively few. However, the empirical findings have been broadly similar to US results. Flectcher [30] examined 101 UK unit trusts from 1980 to 1986 and found positive-selec- tion ability and negative-timing ability. Hallahan and Faff [31] investigated Australian equity trusts from 1988 to 1997 and found limited evidence of timing ability by applying the models of Treynor and Mazuy [32] , Chen and Stockum [33] , and dual-beta. Stevenson [34] examined Irish domiciled funds from 1988 to 2000 by using four alternative models. The results revealed evidence of poor stock-selection ability across the 35 funds tested, while the macro-forecasting results were more varied with some evidence of positive-timing ability in two of the models. Romacho and Cortez [35] investigated the timing and selectivity skills for 21 Portuguese-owned open- end mutual funds by applying the model of Henriksson and Merton [36] . The results showed that managers did not exhibit selectivity and timing abilities, and there was even some evidence of negative timing. Abdel-Kader and Kuang [37] examined the performance of 30 Hong Kong mutual funds from August 1995 to July 2005. They reported that no significant selectivity and timing ability were shown in the results of the actively managed mutual funds. Andrew, Nitzsche and Cuthbertson [38] used the models of Henriksson and Merton and Treynor and Muzuy to examine quarterly returns of 734 UK pooled pension funds, ranging from UK equity to funds specializing in Pacific Basin equities, from March 1980 to December 2004. The non-parametric tests found almost no statistically significant evidence that the managers of these funds generated alpha, or were able to time the market.

Debate on the specification of the selectivity and market-timing models used has also centered on recent studies. Ferson and Schadt [39] argued that controlling for time variation associated with the state of the economy made the average performance as well as the market-timing ability of mutual funds looked better when compared with traditional performance measures. Similar conditional performance evaluations include those of Christopherson, Ferson, and Glassman [40] , Sawicki and Ong [41] , and Ferson and Qian [42] . Several works have extended the study analysis into a multiple portfolio-benchmark framework owing, in part, to the potential problem of misspecification, such as in Connor and Korajczyk [18] and Elton, Gruber, Das and Hlavka [43] . This study approaches the issue of misspecification by applying the general autoregressive conditional heteroscedasticity (GARCH) model proposed by Engle [44] and Bollerslev [45] to capture the characteristic of volatility clustering in time-series data.

Existing studies examining timing and selectivity have often found inconclusive results and related works that discuss the market-timing ability of Taiwan fund managers are also limited. The majority of previous studies on the issue of micro- and macro-forecasting have largely analyzed larger capital markets such as the US and the UK, or a longer sample period such as monthly data. Our study, by looking at a small and thinly traded market, should allow for comparisons to be drawn for any differences in the performance of fund managers based on markets of differing sizes and liquidity. This present study analyzes the 144 Taiwan open-end domestic equity mutual funds from August 2004 to July 2009. One advantage of our study is the use of methodological impro- vement. We extend the time-varying beta method proposed by Chen and Stockum [33] to simultaneously investigate mutual funds’ selectivity, beta stationarity, and timing decisions. The heteroscedasticity of the residual term that might exist in the stochastic beta-parameter model is corrected in the study. We employ the GARCH (1,1) model for adjusting the volatility-clustering nature in a time-series data. In order to regain unbiased and efficient estimators, the generalized least squares (GLS) and a nonlinear-parameter estimate are also used to solve the problem that the residual term is correlated to the independent variable.

The rest of the paper is organized as follows. The following section provides details of the data set used in the study. The third section details the model specification and estimation procedure. Section four presents the empirical results and Section five presents the conclusions.

2. Data

The data used in this paper consists of 144 Taiwan open-end domestic mutual funds obtained from the Taiwan Economic Journal (TEJ) data bank. We study daily returns from August 2004 to July 2009. The fund data are originally classified into eight categories: 1) Common Equity Fund, 2) Medium-Small Capital Fund, 3) High- Tech Fund, 4) Value Stock Fund, 5) Theme Fund, 6) Taiwan Enterprise Fund, 7) Index Fund, and 8) OTC Equity Fund according to the TEJ data bank and the Securities Investment Trust & Consulting Association (SITCA). The Index Fund, belonging to a passive-strategy fund, was deleted from the fund-sample data. For each type of fund, the database contains fund net asset value (NAV), fund daily returns, the daily rate of return of Taiwan Stock Exchange Capitalization Weighted Stock Index (TAIEX), and the one-year deposit rate of the Bank of Taiwan. The one-year deposit rate is then transformed to a daily deposit rate, which is used as the proxy for the risk-free rate. All of the funds available that existed during the sample period are included in the data set. The resulting base sample has a total of 144 equity funds (representing over 80% of the total net assets (TNA) of Taiwan domestic-equity funds), 35 fund companies, 7 fund categories, 1240 daily returns for each fund and a total of approximately 176,580 fund-daily observations over the sample period. Table 1 summarizes the number of funds in each category.

The net asset values and dividends are combined to form a daily return series for each fund 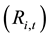as follows:

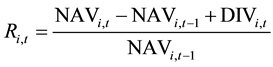, (1)

where 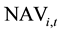is the net asset value of fund on day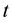, and are the ex-div dividends of fund 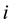on day.

The daily market return series for the TAIEX 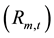is calculated as below:

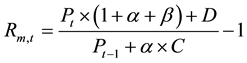(2)

Table 1. The number of funds in each category.

where 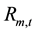is the rate of return of TAIEX on day, 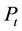is the closing price of TAIEX on day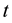, 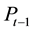is the closing price before the ex-right date on day, is the cash capital increase share distribution rate, is the shareholder stock dividend rate, is the cash capital increase subscription price, and is the cash dividends on ex-cash dividend day.

The one-year deposit rate of the Bank of Taiwan, transformed to the deposit rate on a daily basis as

follows, which is used as the proxy for the daily risk-free rate.

. (3)

3. Methodological Framework

3.1. Stochastic Beta Model

We employ the stochastic beta model proposed by Chen and Stockum (1986) [33] , which can be expressed as

(4)

where is the systematic risk level of fund at time, is the excess return at time, is the mean beta level in the absence of market timing, is changes due to market timing, and is the random error. Equation (4) indicates that the market-timing activity can be active or passive. Active market timing requires the fund managers to shift the portfolio beta according to their expectations. While the random error, , allows the beta of a mutual fund to vary due to nonsystematic factors since the beta of a portfolio may change in the absence of market timing. Thus, should be regarded as a decision variable instead of a fixed coefficient.

Substituting into the ex-post market model in an excess return form of mutual funds as Equation (5) and considering the Autoregressive Conditional Heteroscedasticity (ARCH) effect provide the conditional stochastic-parameter model that is to be estimated as Equation (6):

(5)

, (6)

where is the indicator of stock-selection ability for a fund manager, is a measure of the systematic risk level of mutual fund at time, is the indicator of market-timing ability for a fund manager, is the residual term, and is the conditional variance term of the ARCH effect.

3.2. The Estimation Procedure

The ordinary least-square (OLS) estimation may result in an unbiased but inefficient parameter estimator, since the residual term correlates with the independent variable, (in Equation (6)). Thus we apply the stochastic-parameter model and modify the estimation procedure according to Hildreth and Houck (1968) [46] , which are able to estimate the variance of parameters and deal with the problem of heteroscedasticity. The estimate procedure is as follows.

The first step is to transform the above stochastic-parameter model (6) into the matrix form as Equation (7):

(7)

where represents a column vector of the excess returns, represents an matrix of regressors, denotes a vector of parameters, and is a column vector of the residual term.

The column vector can be further decomposed as:

(8)

where denotes an diagonal matrix with its nonzero elements appear on the main diagonal, represents a column vector with its nth element, is a column vector with its nth element.

The second step is to correct the heteroscedasticity problem using the generalized least squares (GLS) method. We could divide all the regression variables by the following formula:

. (9)

After the above transformation, the best linear GLS estimators, , can be shown as:

(10)

where denotes an diagonal matrix with the diagonal elements. Substitute Equation (8) into, can be further decomposed as below:

(11)

where represents an diagonal matrix with the diagonal elements, and denotes an identity matrix.

The third step is to use the nonlinear-estimation procedure for estimating and. Since direct estimation to separate and for each mutual fund is not available, we need to find a way to measure these two variance parameters. Once and are obtained for each fund, the GLS estimation could be applied.

By using ordinary least squares (OLS) for Equation (7), the residual term can be shown as follows:

(12)

Let, is an idempotent matrix, i.e., and. Thus,

(13)

Substitute Equation (11) into Equation (13), and the variance-covariance matrix of the residual term can be written as:

(14)

Since the values of and are on the diagonal elements, the diagonal elements on both sides of Equation (14) can be written as:

(15)

Let to Equation (15) yields

, (16)

where

: matrix, the square terms of

: vector, the square terms of excess returns

: vector, the diagonal elements of

: vector, the residual terms

, .

If we apply the OLS to Equation (16), it yields

. (17)

Since and are unconditional estimators, by using OLS the parameter estimators might result in negative values, which are unacceptable because both are variance measures. Therefore, we apply a nonlinear-es- timation procedure from SAS Statistical Software and set a restriction that the two parameter estimators must be semipositive. This can be expressed as:

(18)

The fourth step is to estimate the GLS parameter estimators. After we obtain the restricted OLS estimators, and through Equations (3)-(18), the best linear GLS estimators can be estimated as

(19)

where is an diagonal matrix with its diagonal elements,.

The fifth step is to calculate. Substitute the above GLS parameter estimator into Equation (4), and we can obtain the value of for each fund.

To investigate the mutual funds’ beta stationarity, timing, and how the selectivity abilities correlate to the con- ventional fund-performance measurements, the examined alternative hypotheses are generalized as follows:

1) H1: the beta of each fund exhibits the nonstationary behavior;

2) H2-1: each fund manager exhibits stock-selection ability;

3) H2-2: each fund manager exhibits market-timing ability;

4) H3: the stock selectivity and timing abilities positively correlate to the conventional performance measurements such as the Sharpe and Treynor indexes;

5) H4-1: the stock-selection ability differs among the fund categories;

6) H4-2: the market-timing ability differs among the fund categories.

4. Empirical Results

4.1. Tests for Time-Series Data

The results of the ADF test [47] with 10 lags suggest that all the sample fund-return series are stationary. The Ljung-Box tests [48] also reject the null hypothesis of no autocorrelation for the overall fund returns at the 1% level. The ARCH-LM tests with 10 lags suggest the presence of heteroscedasticity in the fund-sample data [44] . In short, these results suggest that the unconditional stochastic beta model would be poorly specified. Therefore, we add the GARCH model into our methodological framework as it takes into account volatility clustering over time [45] .

Similar to the above results of fund returns, the testing results for the market-return series also show stationarity, significant serial correlation, and significant ARCH effects.

4.2. The Random Behavior of the Funds’ Betas

Following the estimate procedure discussed in Section 3, the parameter estimates of the 144 funds being investigated are summarized in Table 2. The parameter estimator of for each mutual fund is obtained through the use of the NLIN procedure and Newton’s method from SAS Statistical Software. As shown in column 1 of

Table 2. Summary Results of Equation (5) and Equation (6).

Table 2, around 86% of the funds (124 out of 144 funds) are found to have random beta behavior, at a 5% level. This measures the non-market oriented source of a mutual fund’s beta nonstationarity. The inclusion of in Equations (3)-(4) allows the beta nonstationarity of mutual funds to be stochastic. This flexibility is desirable as a fund’s beta may be nonstationary even if the fund manager is not engaged in market timing. Figure 1 illustrates the moving pattern of the average beta of 144 funds with the average value 0.8831. This clearly indicates that the systematic risk level, beta, of a mutual fund behaves randomly over time; it is neither a constant nor the dual-beta type as proposed by Henriksson and Merton [36] and Chang and Lewellen [23] .

4.3. The Results of Funds’ Stock Selectivity and Market Timing

4.3.1. Stock Selectivity and Market Timing for the Individual Fund

As shown in Table 2, columns 2, 3, and 4 report funds’ selectivity, target systematic risk, and timing performance. There are 143 positive-selectivity measures and only 1 negative selectivity. However, none of the positive-selectivity measures are statistically significant at the 10% level. This indicates that a significant portion of fund managers are not capable of selecting undervalued securities.

The results of timing performances, measured by, reveal that there are 5 positive performances and 139 negative performances. While the 5 positive performances show statistical insignificance, 119 out of the 139 negative performances are significant at the 5% level. This suggests that none of the mutual funds in the sample could time the market. The results of significantly negative-timing performances may reveal that fund managers tend to operate inversely to the ups and downs of the market. In other words, when the market is up, fund managers may decrease their exposure to stocks and investment. This might be due to the high fund turnover rate and liquidating requirement from fund investors.

Tables 3-5 report the rankings for the individual fund ranked by stock selectivity, timing ability, and the conventional performance measures, respectively. The results of Table 3 show that the top performing funds ranked by the Sharpe index also have better stock-selection ability, contrary to the results of the timing ability in Table 4. As shown in Table 5, the fund rankings by the Sharpe and Treynor indexes are similar and the majority of the sample funds outperform the market. Only 13 out of 144 funds have worse performances than the market when ranked by the Sharpe index and only 4 out of 144 funds underperform when ranked by the Treynor index.

To better understand the relationship between various kinds of fund performance measures, we use the Spearman rank correlation test to examine whether they have similarities in distinguishing fund performances. As reported in Table 6, the Sharpe index, the Treynor index, and the stock-selection ability are highly positively correlated with each other, while the Sharpe index negatively correlates to the market-timing ability but not significantly. Thus we could conjecture that the stock selectivity contributes more than the timing ability to the whole fund performance in our sample data. In addition, Table 6 also shows the negative correlation between stock selectivity and market timing for the individual fund, which indicates a trade-off relationship. In other words, when the market-timing ability is worse, a fund manager’s ability to pick undervalued stocks becomes well, and the reverse is true. This negative-correlation result is consistent with the findings of previous studies.

4.3.2. Stock Selectivity and Market Timing for Different Fund Categories

Table 7 reports the comparison results for the average values of beta, stock selectivity, and market-timing ability. In the case of stock-selectivity ability, the OTC Equity Fund performs better when compared with the other fund categories; while for market-timing ability, the Value Stock Fund performs relatively better than the other

Figure 1. The moving pattern of the average beta. This figure shows the moving pattern of the average beta for the 144 sample funds. The value of the average beta is 0.8831.

Table 3. Individual fund ranking by stock selectivity and the Sharpe index.

Table 4. Individual fund ranking by timing ability and the Sharpe index.

Table 5. Individual fund ranking by the Sharpe index and Treynor index.

Table 6. The results of the Spearman correlation test for performance measures.

Table 7. Comparison results for the average values of beta, stock selectivity, and market-timing ability.

fund categories although the timing ability shows negative values. The insignificantly negative-timing ability for the Theme Fund and the Value Stock Fund is due to the investigated sub-samples being too small. Interestingly, the rankings of seven fund categories seem to show a negative relationship between the stock selectivity and timing ability. Last, in the case of the average beta, the High-Tech Fund has the highest beta, 0.8960; next is the Common Equity Fund and the lowest is the Taiwan Enterprise Fund. This seems to be consistent with the fact that high-tech stocks usually have higher trading volumes in Taiwan Stock Exchange. In addition, the average value of betas for all seven fund categories are less than one, which indicates that fund managers tend to be more conservative or less active in the study sample period in order to avoid losing in the financial crisis.

Table 8 and Table 9 report the results of analysis of variance (ANOVA) test and Duncan test for the seven fund categories ranked by stock selectivity and market-timing ability, respectively. The significant F value of the ANOVA test, whether in the case of stock selectivity or timing ability, indicates that significant differences exist between the seven fund categories. The results of the Duncan test in Table 8 show that the OTC Equity Fund has superior stock-selection ability than the High-Tech Fund, the Common Equity Fund, and the Value Stock Fund. Moreover, the Medium-Small Capital Fund performs better in stock selectivity than the Value Stock Fund. On the other hand, in the case of market-timing ability, the Value Stock Fund outperforms the Taiwan Enterprise Fund, the Medium-Small Capital Fund and the OTC Equity Fund. The Common Equity Fund, High-Tech Fund, and Theme Fund outperform the Medium-Small Capital Fund and the OTC Equity Fund, while the Taiwan Enterprise Fund performs better than the OTC Equity Fund.

5. Conclusions

In contrast to conventional performance measures based on constant systematic risk, this study aims to examine mutual funds’ stock selectivity and timing ability on the basis of allowing the funds’ systematic risk levels to change due to both the timing decisions and the non-market oriented factors. To better specify the fund-perfor- mance measures and increase the efficiency of the parameter estimators, this study also takes into account the heteroscedasticity that might exist in the stochastic beta model. A number of results emerge from this study, which can be summarized as follows.

First, the systematic risk levels of mutual funds are found to be nonstationary, consistent with the findings of many previous studies on the US fund data [7] [33] [49] . This result reveals that the beta nonstationarity is caused by market timing (the market factor) and random behavior (the non-market factor). Additionally, the average value of beta coefficients for all the sample funds is found to be less than one. This might be due to more conservative management strategy on the part of fund managers caused by the international financial crisis dur-

Table 8. The results of the ANOVA test and Duncan test for the seven fund categories ranked by stock electivity α.

*represents the significance at the 10% level.

Table 9. The results of the ANOVA test and Duncan test for the seven fund categories ranked by market timing ability δ1.

*represents the significance at the 10% level.

ing our study period.

Second, our empirical study results in positive but not significant stock selectivity and significantly negative-timing ability. This implies that Taiwan open-end domestic equity funds, on average, do not have stock-se- lection ability and market-timing ability although over 90% of the Taiwan domestic equity funds outperform the market when measured in terms of the Sharpe and Treynor indexes. The negative-timing ability implies that the fund managers tend to operate inversely to whether the market is up or down. This might be due to the high turnover rate of the Taiwan fund market and that fund managers liquidate the redemption requirement from investors. These results seem to be consistent with the EMH.

Third, the empirical results show a negative relationship between stock selectivity and timing ability in different fund categories. For an individual fund, the results also show a trade-off relationship between stock selectivity and timing ability. The analysis of the Spearman correlation test shows that the stock selectivity has similar distinguishability to conventional performance measures such as the Sharpe and Treynor indexes, while timing ability negatively correlates to the Sharpe index, but not significantly.

Last, both the stock selectivity and timing ability are found to be significantly different between different fund categories. The OTC Equity Fund has superior stock selectivity while the Value Stock Fund has relatively better market-timing ability. This seems to imply that there are more bargain buys in the OTC market and that the price fluctuation of the undervalued stocks could be irrelative to the market factor.

This paper examines funds’ selectivity, beta stationary, and timing decisions simultaneously by a time-vary- ing beta model. GARCH, GLS and a nonlinear parameter-estimator model are applied to increase the estimate efficiency. The application to other instances of multi-factor model may be considered in the future.

References

  1. Sharpe, W.F. (1966) Mutual Fund Performance. The Journal of Business, 39, 119-138. http://dx.doi.org/10.1086/294846
  2. Treynor, J.L. (1965) How to Rate Management of Investment Funds. Harvard Business Review, 43, 63-75.
  3. Jensen, M.C. (1968) The Performance of Mutual Funds in the Period 1945-1964. The Journal of Finance, 23, 389-416. http://dx.doi.org/10.1111/j.1540-6261.1968.tb00815.x
  4. Klemkosy, R.C. and Maness, T.S. (1978) The Predictability of Real Portfolio Risk Levels. The Journal of Finance, 33, 631-639. http://dx.doi.org/10.1111/j.1540-6261.1978.tb04873.x
  5. Kon, S.J. and Jen, F.C. (1978) Estimation of Time-Varying Systematic Risk and Performance of Mutual Fund Portfolios: An Application of Switching Regression. The Journal of Finance, 33, 457-475. http://dx.doi.org/10.1111/j.1540-6261.1978.tb04861.x
  6. Fabozzi, F.J. and Francis, J.C. (1979) Mutual Fund Systematic Risk for Bull and Bear Markets: An Empirical Investigation. The Journal of Finance, 34, 1243-1250. http://dx.doi.org/10.1111/j.1540-6261.1979.tb00069.x
  7. Francis, J.C. and Fabozzi, F.J. (1980) Stability of Mutual Fund Systematic Risk Statistic. Journal of Business Research, 8, 263-275. http://dx.doi.org/10.1016/0148-2963(80)90014-4
  8. Miller, T.W. and Gressis, N. (1980) Nonstationary and Evaluation of Mutual Fund Performance. The Journal of Financial and Quantative Analysis, 15, 639-654. http://dx.doi.org/10.2307/2330402
  9. Radcliffe, R., Brooks, R. and Levy, H. (1993) Active Timing Decisions of Equity Mutual Funds. Financial Service Review, 2, 21-39. http://dx.doi.org/10.1016/1057-0810(92)90013-3
  10. Golec, J.H. (1996) The Effects of Mutual Fund Managers’ Characteristics on Their Portfolio Performance, Risk and Fees. Financial Services Review, 5, 133-147. http://dx.doi.org/10.1016/S1057-0810(96)90006-2
  11. Busse, J.A. (2001) Another Look at Mutual Fund Tournaments. Journal of Financial and Quantitative Analysis, 36, 53-73. http://dx.doi.org/10.2307/2676197
  12. Matallín, J.C. and Fernández-Izquierdo, A. (2003) Passive Timing Effect in Portfolio Management. Applied Economics, 35, 1829-1837. http://dx.doi.org/10.1080/0003684032000150404
  13. Fama, E.F. (1972) Components of Investment Performance. Journal of Finance, 27, 551-567.
  14. Kon, S.J. (1983) The Market Timing Performance of Mutual Fund Managers. Journal of Business, 56, 323-347. http://dx.doi.org/10.1086/296204
  15. Lehman, B.N. and Modest, D.M. (1987) Mutual Fund Performance Evaluation: A Comparison of Benchmark and Non- Benchmark Comparisons. Journal of Finance, 42, 233-265. http://dx.doi.org/10.1111/j.1540-6261.1987.tb02566.x
  16. Grinblatt, M. and Titman, S. (1989) Portfolio Performance Evaluation: Old Issues and New Insights. Review of Financial Studies, 2, 393-421. http://dx.doi.org/10.1093/rfs/2.3.393
  17. Cumby, R.E. and Glen, J.D. (1990) Evaluation the Performance of International Mutual Funds, Journal of Finance, 45, 497-521. http://dx.doi.org/10.1111/j.1540-6261.1990.tb03700.x
  18. Connor, G. and Korajczyk, R.A. (1991) The Attributes, Behavior and Performance of US Mutual Funds. Review of Quantitative Finance and Accounting, 1, 5-26. http://dx.doi.org/10.1007/BF02408404
  19. Coggin, T.D., Fabozzi, F.J. and Rahman, S. (1993) The Investment Performance of US Equity Pension Fund Managers: An Empirical Investigation. Journal of Finance, 48, 1039-1056. http://dx.doi.org/10.1111/j.1540-6261.1993.tb04029.x
  20. Coggin, T.D. and Hunter, J.E. (1991) A Meta-Analysis of Mutual Fund Performance. Review of Quantitative Finance and Accounting, 3, 189-201. http://dx.doi.org/10.1007/BF02407005
  21. Dellva, W.L., DeMaskey, A.L. and Smith, C.A. (2001) Selectivity and Market Timing Performance of Fidelity Sector Mutual Funds. Financial Review, 36, 39-54. http://dx.doi.org/10.1111/j.1540-6288.2001.tb00003.x
  22. Henriksson, R.D. (1984) Market Timing and Mutual Fund Performance: An Empirical Investigation. The Journal of Business, 57, 73-96. http://dx.doi.org/10.1086/296225
  23. Chang, E.C. and Lewellen, W.G. (1984) Market Timing and Mutual Fund Investment Performance. Journal of Business, 57, 57-72. http://dx.doi.org/10.1086/296224
  24. Kao, G.W., Cheng, T.W. and Chan, K.C. (1998) International Mutual Fund Selectivity and Market Timing during Up and Down Market Conditions. The Financial Review, 33, 127-144. http://dx.doi.org/10.1111/j.1540-6288.1998.tb01373.x
  25. Grinblatt, M. and Titman, S. (1993) Performance Measurement without Benchmarks: An Examination of Mutual Fund Returns. Journal of Business, 66, 47-68. http://dx.doi.org/10.1086/296593
  26. Wermers, R. (1997) Momentum Investment Strategies of Mutual Funds, Performance Persistence, and Survivorship Bias. Working Paper, University of Colorado, Denver.
  27. Wermers, R. (2000) Mutual Fund Performance: An Empirical Decomposition into Stock-Picking Talent, Style, Transactions Costs, and Expenses. Journal of Finance, 55, 1655-1703. http://dx.doi.org/10.1111/0022-1082.00263
  28. Lee, C.F. and Rahman, S. (1990) Market Timing, Selectivity, and Mutual Fund Performance: An Empirical Investigation. Journal of Business, 63, 261-278. http://dx.doi.org/10.1086/296505
  29. Bollen, P.B. and Busse, J.A. (2001) On the Timing Ability of Mutual Fund Managers. Journal of Finance, 56, 1075- 1094. http://dx.doi.org/10.1111/0022-1082.00356
  30. Flectcher, J. (1995) An Examination of Selectivity and Market Timing Performance of UK Unit Trusts. Journal of Business Finance & Accounting, 22, 143-156. http://dx.doi.org/10.1111/j.1468-5957.1995.tb00676.x
  31. Hallahan, T.A. and Faff, R.W. (1999) An Examination of Australian Equity Trusts for Selectivity and Market Timing Performance. Journal of Multinational Financial Management, 9, 387-402. http://dx.doi.org/10.1016/S1042-444X(99)00008-0
  32. Treynor, J.L. and Mazuy, K. (1966) Can Mutual Fund Outguess the Market? Harvard Business Review, 44, 131-136.
  33. Chen, C.R. and Stockum, S. (1986) Selectivity, Market Timing and Random Beta Behavior of Mutual Funds: A Generalized Model. Journal of Financial Research, 9, 87-96. http://dx.doi.org/10.1111/j.1475-6803.1986.tb00437.x
  34. Stevenson, S. (2004) A Performance Evaluation of Portfolio Managers: Tests of Micro and Macro Forecasting. The European Journal of Finance, 10, 391-411. http://dx.doi.org/10.1080/1351847032000143413
  35. Romacho, J.C. and Cortez, M.C. (2006) Timing and Selectivity in Portuguese Mutual Fund Performance. Research in International Business & Finance, 20, 348-368. http://dx.doi.org/10.1016/j.ribaf.2005.05.005
  36. Henriksson, R.D. and Merton, R.C. (1981) On Market Timing and Investment Performance. II. Statistical Procedures for Evaluating Forecasting Skills. Journal of Business, 54, 513-533. http://dx.doi.org/10.1086/296144
  37. Abdel-Kader, M. and Kuang, Y.Q. (2007) Risk-Adjusted Performance, Selectivity, Timing Ability and Performance Persistence of Hong Kong Mutual Funds. Journal of Asia-Pacific Business, 8, 25-58. http://dx.doi.org/10.1300/J098v08n02_03
  38. Andrew, C., Nitzsche, D. and Cuthbertson, K. (2009) An Empirical Investigation into the Performance of UK Pension Fund Managers. Journal of Pension Economics and Finance, 9, 533-547.
  39. Ferson, W.E. and Schadt, R.W. (1996) Measuring Fund Strategy and Performance in Changing Economic Conditions. Journal of Finance, 51, 425-461. http://dx.doi.org/10.1111/j.1540-6261.1996.tb02690.x
  40. Christopherson, J.A., Ferson, W.E. and Glassman, D.A. (1998) Conditioning Manager Alphas on Economic Information: Another Look at the Persistence of Performance. Review of Financial Studies, 11, 111-142. http://dx.doi.org/10.1093/rfs/11.1.111
  41. Sawicki, J. and Ong, F. (2000) Evaluating Managed Fund Performance Using Conditional Measures: Australian Evidence. Pacific-Basin Finance Journal, 8, 505-528. http://dx.doi.org/10.1016/S0927-538X(00)00027-5
  42. Ferson, W.E. and Qian, M. (2004) Conditional Performance Evaluation, Revisited. The Research Foundation of CFA Institute Press. http://www-bcf.usc.edu/~ferson/papers/CPE.PDF
  43. Elton, E.J., Gruber, M.J., Das, S. and Hlavka, M. (1993) Efficiency with Costly Information: A Reinterpretation of Evidence form Managed Portfolios. Review of Financial Studies, 6, 1-22. http://dx.doi.org/10.1093/rfs/6.1.1
  44. Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. http://dx.doi.org/10.2307/1912773
  45. Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroscedasticity. Journal of Econometrics, 31, 307-327. http://dx.doi.org/10.1016/0304-4076(86)90063-1
  46. Hildreth, C. and Houck, J.P. (1968) Some Estimators for a Linear Model with Random Coefficients. Journal of American Statistical Association, 63, 584-595.
  47. Dickey, D.A. and Fuller, W.A. (1981) Likelihood Ratio Statistics for Autoregressive Time Series with Unit Root. Eco- nometrica, 49, 1057-1072. http://dx.doi.org/10.2307/1912517
  48. Ljung, G.M. and Box, G.E.P. (1978) On a Measure of Lack of Fit in Time Series Models. Biometrika, 65, 297-303. http://dx.doi.org/10.1093/biomet/65.2.297
  49. Lockwood, L.J. and Kadiyala, K.R. (1988) Measuring Investment Performance with a Stochastic Parameter Regression Model. Journal of Banking and Finance, 12, 457-467. http://dx.doi.org/10.1016/0378-4266(88)90009-X

NOTES

*Corresponding author.

Journal Menu >>