Modern Economy
Vol. 4 No. 7 (2013) , Article ID: 34706 , 11 pages DOI:10.4236/me.2013.47051
Exchange Rate and Current Account Dynamics with Habits over Consumption and Money Holdings
1Faculty of Economics, Ritsumeikan University, Kusatsu, Japan
2Institute of Social and Economic Research, Osaka University, Ibaraki, Japan
Email: *gombi@ec.ritsumei.ac.jp
Copyright © 2013 Ichiro Gombi, Shinsuke Ikeda. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 18, 2013; revised March 30, 2013; accepted April 30, 2013
Keywords: Habit formation; Money; Exchange rate; Current account
ABSTRACT
Incorporating two independent habits over consumption and money holdings into a small country model, we examine the adjustment dynamics of the current account and the exchange rate to expansionary monetary and fiscal shocks under two alternative policy regimes: (1) the endogenous income transfer regime; and (2) the endogenous fiscal spending regime. In response to the shocks under regime (1), the exchange rate depreciates on impact and in the long run whereas it appreciates (depreciates) in transition if preferences for real money balances exhibit distant (adjacent) complementarity. Under regime (2), the consumption habits and the monetary habits jointly generate possibly non-monotonic current account dynamics. An induced increase in fiscal spending in regime (2) can generate a current account surplus in the case where the monetary habits exhibit strong distant complementarity.
1. Introduction
The academic as well as practical concerns about the fluctuation of exchange rates and the movement of the current account grow as the integration of the world economy progresses in the recent decades. To describe jointly the dynamics of exchange rates and the current account, there has been cumulative theoretical research that is conducted in the dynamic optimization framework. The seminal work by Obstfeld [1] is the first attempt, which specifies consumer preferences in such non-time separable form as endogenous time preferences. Mansoorian [2] and other related articles (e.g., Mansoorian and Neaime [3]) propose habit models as an alternative empirically relevant specification to examine monetary phenomena in the open economy setting. Although the studies successfully show that incorporating habit formation helps to understand open macroeconomic phenomena, the framework is restricted in the following two aspects: first, the crawling peg exchange-rate regime is assumed, so that the exchange rate is exogenously given; second, habit is specified over the sub-utility defined as the homothetic bundle of consumption and real money balances. Although these specifications enable one to apply straightforwardly the implication of habit formation to monetary issues of open economies, we need a more comprehensive framework to examine the exchangerate and current-account dynamics by focusing on specific roles that are played by habits over real money balances and over consumption.
The purpose of this article is to do it: we examine the dynamic adjustment of the current account and the exchange rate to monetary and fiscal policies by introducing the money-specific habits as well as the consumption-specific habits in the form of weakly nonseparable preferences.1 This specification of habits enables us to allow for different degrees of habit strength between consumption and money.2 Whereas consumer preferences are assumed to be of the type of adjacent complementarity,3 we will not put any restriction on the degree of monetary habits because there is no empirical report on the strength of habits on real money balances.
By assuming that the government’s budget is always balanced we analyze the effects of macroeconomic policies under two alternative regimes: (1) the endogenous income transfer regime, in which income transfer payments (τ) are endogenously determined so as to retain the balanced budget for exogenous values of the money growth rate (μ) and of fiscal spending (g); and (2) the endogenous fiscal spending regime, in which g is endogenously determined so as to balance the budget for exogenous μ and τ .
The results of comparative dynamics that we shall show are summarized in Table 1, where the results of [1] and [2] are also listed for comparison. In the endogenous income transfer regime (see column (1)), we consider the effects of monetary policy (an increase in μ) and fiscal policy (an increase in g) separately. For the monetary policy we show that the “super neutrality of money” holds valid in the present habit model: on impact and in the long run, the policy does not affect real sector variables, with making real money balances decrease and hence the exchange rate depreciate. In transition, the exchange rate is shown to depreciate or appreciate as preferences for real money balances exhibit adjacent or distant complementarity (i.e., AC or DC in the table). The fiscal policy exerts similar effects on those monetary variables due to a negative income effect. With habit persistence of consumption, on the other hand, the policy induces the current account deficit as in the familiar argument of the Keynesian type (e.g., Mansoorian [10]).
In the endogenous fiscal spending regime (as shown in column (2)), since a change in inflation tax revenues affects fiscal spending, changes in real money balances directly affect the current account. Habit formation over real money balances as well as that over consumption thus plays critical roles in generating the current account dynamics. The resulting effects on net foreign assets depend on the intertemporal complementarities of real money balances as well as of consumption. For example, although preferences for consumption are assumed to be of adjacent complementarity, the induced increase in fiscal spending causes a current account surplus if preferences for real money balances exhibit strong distant complementarity. The transition dynamics of the net foreign assets are shown to be non-monotonic under certain conditions.
To our knowledge, Shi and Epstein [11] is the unique study which addresses the exchange rate dynamics using a habit model. By incorporating habits into an endogenous time preference model of the Uzawa type, they derive cyclical dynamics of the current account and the exchange rate. However, Shi and Epstein consider habits over the homothetic bundle of consumption and money, in which habits of consumption and those of real money balances do not play independent roles. Their model also retains the same (undesirable) property for the steady state equilibrium as the models with the Uzawa utility (e.g., [1]) has. For example, an increase in fiscal spending causes long-run accumulation of external assets (see column (3) of Table 1). By resolving these problems, we reexamine the exchange-rate/current-account dynamics

Table 1. The main results of comparative dynamics.
using a habit model.
The remainder of the paper is structured as follows: In Section 2, we present a small open monetary model with habit formation. In the following Sections 3 and 4, we examine equilibrium dynamics of consumption, real money balances, exchange rates, and net foreign assets, and analyze the effects of macroeconomic policies on the current account and the exchange rate. The effects of monetary policy and fiscal policy under the endogenous income transfer regime are analyzed in Section 3. We analyze the effect of mixed monetary policy with fiscal policy under the endogenous fiscal spending regime, and then show possibilities of non-monotonic current account dynamics in Section 4. Section 5 concludes the paper.
2. The Model
Consider a small open monetary economy where identical agents live infinitely. There is only one internationally traded good in the model. Since the foreign price of the good is assumed to be constant, the rate of inflation (the rate of change in the domestic price of the good) is equal to the rate of depreciation of the domestic currency, which is denoted by εt. The representative agent is endowed with constant units  of the good and consumes some of the good
of the good and consumes some of the good 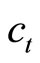 at each instant. He holds non-human wealth in the form of real money balances
at each instant. He holds non-human wealth in the form of real money balances 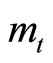 and/or internationally traded bonds
and/or internationally traded bonds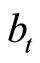 , which yields a constant interest rate
, which yields a constant interest rate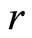 . He faces the following flow budget constraint:
. He faces the following flow budget constraint:
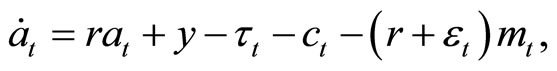 (1)
(1)
where total wealth 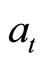 defined as
defined as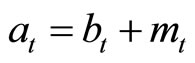 ,
, 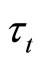 denotes lump-sum income transfer to the government, and a dot over a variable denotes the time derivative of the variable through the paper.
denotes lump-sum income transfer to the government, and a dot over a variable denotes the time derivative of the variable through the paper.
Consumption and real money balances affect utility directly as well as indirectly through forming habits. Let 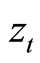 and
and  represent the habit capitals with respect to consumption and real money balances, respectively. We specify
represent the habit capitals with respect to consumption and real money balances, respectively. We specify  and
and 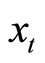 as
as
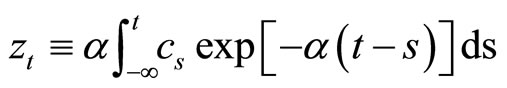
and
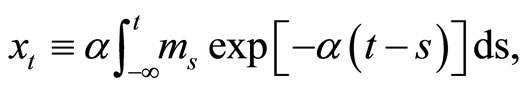
equivalently:
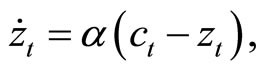 (2)
(2)
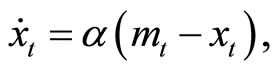 (3)
(3)
where 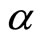 represents the velocity of habit formation. For brevity, we have assumed that the habit velocity
represents the velocity of habit formation. For brevity, we have assumed that the habit velocity 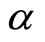 is common for
is common for  and
and . The representative agent maximizes the following lifetime utility
. The representative agent maximizes the following lifetime utility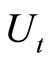 :
:
 (4)
(4)
where 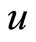 and
and 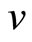 represent felicity functions and where, to ensure the existence of the steady-state equilibrium, we assume that the discount rate is equal to the world interest rate
represent felicity functions and where, to ensure the existence of the steady-state equilibrium, we assume that the discount rate is equal to the world interest rate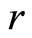 . Function
. Function  is assumed to satisfy the standard regularity conditions: (C1)
is assumed to satisfy the standard regularity conditions: (C1) 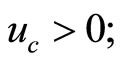 (C2)
(C2) 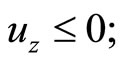 (C3)
(C3)  (C4)
(C4) 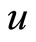 is concave in (c,z) (C5)
is concave in (c,z) (C5) 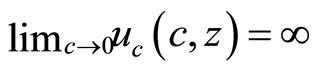 uniformly in
uniformly in  and (C6)
and (C6)
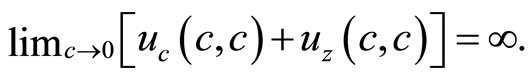
Function  is specified in the same way. The additive separable specification of the utility functions allows us to introduce weak nonseparability caused by habits, where habits of consumption and real money balances independently affect total expenditure and hence wealth accumulation.
is specified in the same way. The additive separable specification of the utility functions allows us to introduce weak nonseparability caused by habits, where habits of consumption and real money balances independently affect total expenditure and hence wealth accumulation.
As in Ryder and Heal [12], preference for consumption time-profile is said to display adjacent (distant) complementarity when

where an increase in today’s habits ceteris paribus enlarges (decreases) today's optimal consumption. Adjacent and distant complementarities of the preference for the time-profile of real money balances are defined similarly in terms of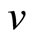 .
.
The government’s flow budget constraint is specified as:
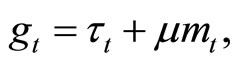 (5)
(5)
where 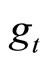 represents fiscal spending,
represents fiscal spending,  does the growth rate of nominal money balances.
does the growth rate of nominal money balances.
We shall consider two alternative policy regimes: (R1) the endogenous income transfer regime, in which fiscal spending  is constant and lump-sum tax
is constant and lump-sum tax 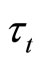 is chosen by the government in order to satisfy its constraint (5); and (R2) the endogenous fiscal spending regime, where lump-sum tax
is chosen by the government in order to satisfy its constraint (5); and (R2) the endogenous fiscal spending regime, where lump-sum tax 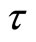 is constant and fiscal spending
is constant and fiscal spending 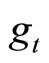 is determined so as to satisfy (5). In the endogenous income transfer regime, raising
is determined so as to satisfy (5). In the endogenous income transfer regime, raising  as a fiscal policy and raising
as a fiscal policy and raising 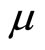 as a monetary policy are independent policy instruments, whereas, in the endogenous fiscal policy regime, the monetary policy of raising
as a monetary policy are independent policy instruments, whereas, in the endogenous fiscal policy regime, the monetary policy of raising 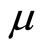 inevitably changes fiscal spending
inevitably changes fiscal spending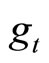 , so that the two macroeconomic policies simultaneously affect the economy. In Section 3, we shall examine the effects of monetary and fiscal policies separately in the endogenous income transfer regime. Section 4, in turn, explores the combined effect of the mixed monetary policy in the endogenous fiscal spending regime.
, so that the two macroeconomic policies simultaneously affect the economy. In Section 3, we shall examine the effects of monetary and fiscal policies separately in the endogenous income transfer regime. Section 4, in turn, explores the combined effect of the mixed monetary policy in the endogenous fiscal spending regime.
From the definition of real money balance, its growth is shown as:
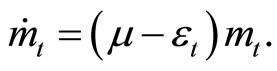 (6)
(6)
To ease terminology, we say that the domestic currency is appreciating (depreciating) when the rate of change in the exchange rate 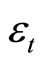 is lower (higher) than the long-run core rate of inflation
is lower (higher) than the long-run core rate of inflation 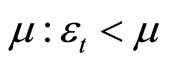
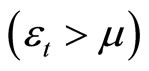 . With the terminology,
. With the terminology, when
when 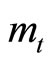 increases (decreases) over time, domestic currency is appreciating (depreciating) as shown in Figure 1.
increases (decreases) over time, domestic currency is appreciating (depreciating) as shown in Figure 1.
Now we can define the representative agent’s optimization problem as follows. Given the initial values  the representative agent chooses
the representative agent chooses
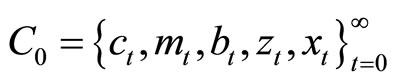
so as to maximize (4) subject to: (c1) the flow budget constraint (1); (c2) the habit formation of consumption (2) and of real money balances (3); and (c3) the transversality conditions.
After solving the representative agent’s problem,4 we obtain that consumption habit z follows the autonomous dynamics:
 (7)
(7)
where the stable root of the autonomous dynamics  is defined as
is defined as
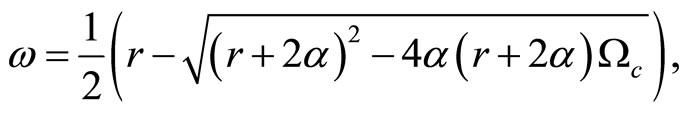 (8)
(8)
where:
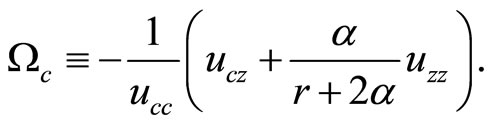 (9)
(9)
A positive (negative) 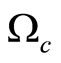 implies adjacent (distant) complementarity for
implies adjacent (distant) complementarity for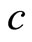 .
.
We substitute this saddle trajectory (7) into (2) to obtain:
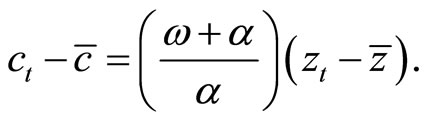 (10)
(10)
To simplify discussion below, we focus on the case of adjacent complementarity, which is empirically relevant as shown in, e.g., Ferson and Constantinides [6] and Gurber [14].
Assumption 1. The representative agent’s preferences exhibit adjacent complementarity for consumption profile, i.e.,  and hence
and hence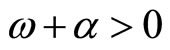 .
.
Solving the representative agent problem also yields the result that monetary habit capital 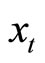 follows the autonomous dynamics (see Appendix A in [13] for derivation):
follows the autonomous dynamics (see Appendix A in [13] for derivation):
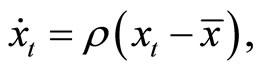 (11)
(11)
 (a)
(a)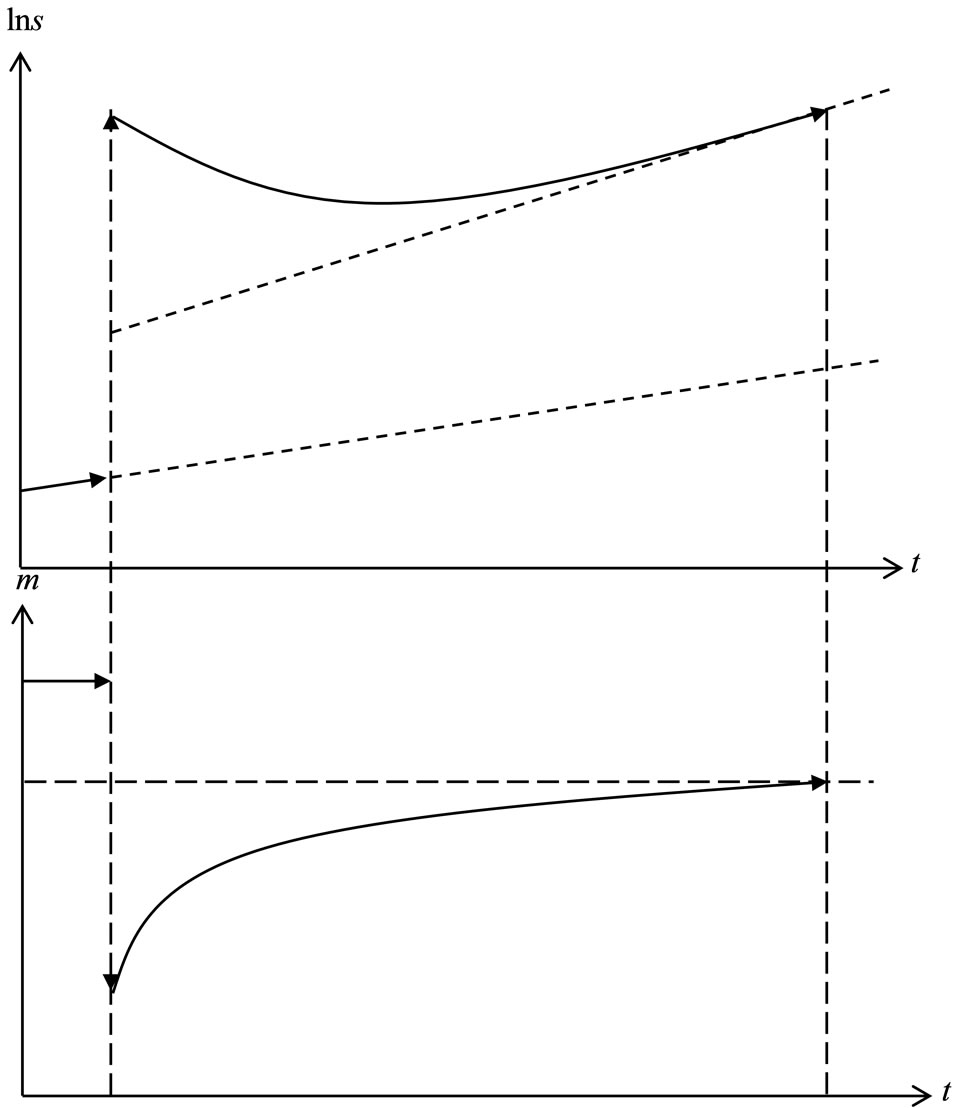 (b)
(b)
Figure 1. Equilibrium dynamics of exchange rate s and real money balances m. (a) Currency Depreciation: ε > μ when α + ρ > 0; (b) Currency Appreciation: ε > μ when α + ρ < 0.
where the root of the autonomous dynamics is denoted as . The saddle-point stability condition of the dynamics, i.e.,
. The saddle-point stability condition of the dynamics, i.e.,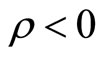 , is satisfied if and only if
, is satisfied if and only if
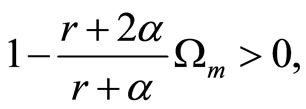
where
 which is positive (negative) when preferences for real money balances are of the type of adjacent (distant) complementarity. We assume the above saddle-point stability condition.
which is positive (negative) when preferences for real money balances are of the type of adjacent (distant) complementarity. We assume the above saddle-point stability condition.
Substituting (11) into (3) yields:
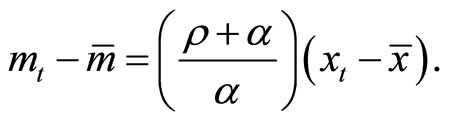 (12)
(12)
As in the case of the consumption-habit dynamics (10), the sign of ρ + α is positive (negative) when preferences for real money balances are of the type of adjacent (distant) complementarity.
As shown in Appendix B of [13], we obtain that
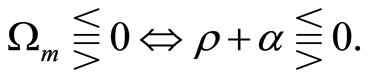
This relationship and (12) imply the following property:
Property 1. Real money balances  positively (negatively) comove with their habits
positively (negatively) comove with their habits  if preferences for real money balances exhibit adjacent (distant) complementarity,
if preferences for real money balances exhibit adjacent (distant) complementarity, 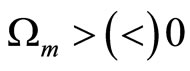 and hence
and hence .
.
Figure 2 illustrates Property 1. Although preferences for consumption have been often reported to display adjacent complementarities, there is no empirical evidence regarding habit-forming behavior of real money balances. Therefore, we do not put any restriction on the sign of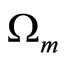 .
.
In the present setting of weak nonseparability, relationship between (10) and (12) can be specified for consumption and money balance holdings, wherein we characterize the consumer preferences by using the following terminology:
Definition 1. Consuming good is said to be more (less) habit forming than holding real money balances if  is larger (smaller) than
is larger (smaller) than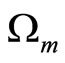 , and hence if
, and hence if  is larger (smaller) than
is larger (smaller) than .
.
Combining the representative agent’s flow constraint (1) and the government’s flow constraint (5), we obtain the balance-of-payment equation as follows:
 (13)
(13)
3. Endogenous Income-Transfer Regime
Start with the endogenous income-transfer regime. Since the dynamics of real money balances and their habits do not directly affect the balance-of-payment Equation (13), the dynamics of 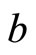 are generated only
are generated only
 (a)
(a) (b)
(b)
Figure 2. Saddle path dynamics of real money balances m and it’s monetary habits z. (a) Adjacent complementarity: α + ρ > 0; (b) Distant complementarity: α + ρ < 0.
by consumption-habit capital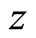 . Let us set local deviations
. Let us set local deviations  equal to
equal to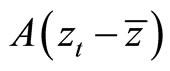 , where
, where  is an undetermined constant. We linearize (13) around the steady-state point and substitute
is an undetermined constant. We linearize (13) around the steady-state point and substitute 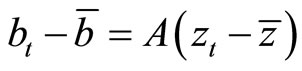 into the result. By determining
into the result. By determining 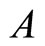 such that they satisfy (13), the equilibrium dynamics of
such that they satisfy (13), the equilibrium dynamics of 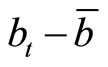 are obtained as:
are obtained as:
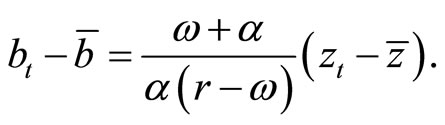 (14)
(14)
For given initial values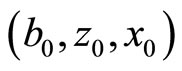 , the steady-state equilibrium
, the steady-state equilibrium 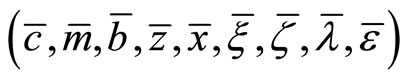 is determined by the following nine equations:
is determined by the following nine equations:
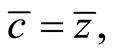 (15)
(15)
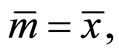 (16)
(16)
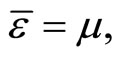 (17)
(17)
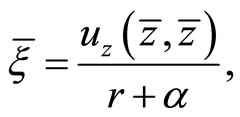 (18)
(18)
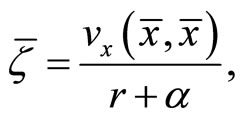 (19)
(19)
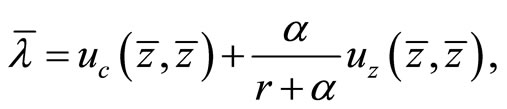 (20)
(20)
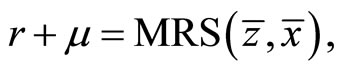 (21)
(21)
 (22)
(22)
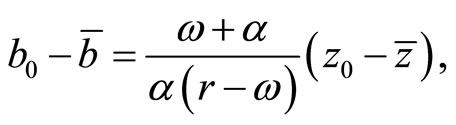 (23)
(23)
where MRS represents the steady-state marginal rate of substitution between 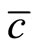 and
and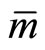 :
:

3.1. The Effect of Monetary Policy
Since (22) and (23) do not contain the monetary variables m, x and 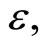 the monetary policy here, i.e., a helicopterdropped change in
the monetary policy here, i.e., a helicopterdropped change in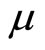 , is perfectly neutral to the consumption-related variables c,
, is perfectly neutral to the consumption-related variables c, 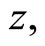 and
and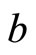 .5 From (21), an increase in
.5 From (21), an increase in 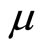 only reduces the steady-state level of real money balances
only reduces the steady-state level of real money balances , which causes the dynamic adjustment of the money-related variables
, which causes the dynamic adjustment of the money-related variables 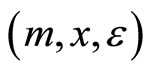 with leaving the steady-state values of
with leaving the steady-state values of 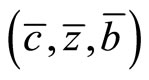 unchanged, where the dynamics of the money-related variables follow Property 1.
unchanged, where the dynamics of the money-related variables follow Property 1.
This implies that an increase in costs of holding money due to a rise in 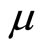 discretely reduces real money balances and thereby causing the exchange rate to sharply depreciate on impact. Thereafter, if preferences for real money balances exhibit adjacent(distant) complementarity, real money balances gradually decrease (increase) and hence, the exchange rate experiences further depreciation (inversely appreciation) in entire transition.
discretely reduces real money balances and thereby causing the exchange rate to sharply depreciate on impact. Thereafter, if preferences for real money balances exhibit adjacent(distant) complementarity, real money balances gradually decrease (increase) and hence, the exchange rate experiences further depreciation (inversely appreciation) in entire transition.
These results can be summarized as the following proposition:
Proposition 1. Suppose that the government adopts the endogenous income-transfer regime. Then, a permanent increase in the monetary growth rate is ineffective on the consumption-related variables c, z and b. In response to the policy1) on impact and in the long-run, real money balances decrease and hence the exchange rate depreciates; and 2) in transition, exchange-rate depreciation (appreciation) takes place when liquidity preferences exhibit adjacent (distant) complementarity.
Figures 1 and 2 illustrate the equilibrium dynamics that are obtained in Proposition 1, where, in panels (a) and (b) of Figure 2, points  and
and 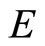 represent the preand post-shock equilibrium points. Although the dynamics of real money balances for adjacent complementarity (panel (a) in Figure 2), i.e., an initial discrete reduction and subsequent over-time decrease, are similar to what Mansoorian [2] shows using a habit model of the crawling pegged exchange rate regime (as shown in column (4) of Table 1), the adjustment in our model is brought about by an initial discrete depreciation followed by over-time depreciation of the domestic currency value (see panel (a) of Figure 1). When liquidity preferences exhibit distant complementarity, in contrast, the initial discrete depreciation is so large that the exchange rate therefore appreciates over time, as Obstfeld [1] shows with using an endogenous time-preference model (see column (3) of Table 1). Unlike in those previous models, consumption and the current account here are not affected by the monetary policy.
represent the preand post-shock equilibrium points. Although the dynamics of real money balances for adjacent complementarity (panel (a) in Figure 2), i.e., an initial discrete reduction and subsequent over-time decrease, are similar to what Mansoorian [2] shows using a habit model of the crawling pegged exchange rate regime (as shown in column (4) of Table 1), the adjustment in our model is brought about by an initial discrete depreciation followed by over-time depreciation of the domestic currency value (see panel (a) of Figure 1). When liquidity preferences exhibit distant complementarity, in contrast, the initial discrete depreciation is so large that the exchange rate therefore appreciates over time, as Obstfeld [1] shows with using an endogenous time-preference model (see column (3) of Table 1). Unlike in those previous models, consumption and the current account here are not affected by the monetary policy.
3.2. The Effect of Fiscal Policy
Let us next analyze the steady-state effects of a onceand-for-all increase in fiscal spending g. Differentiating (21), (22) and (23) with respect to g, we obtain the steady-state effects on 
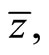 and
and 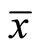 as follows:
as follows:
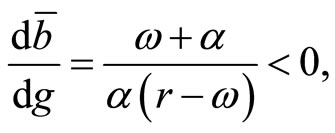 (24)
(24)
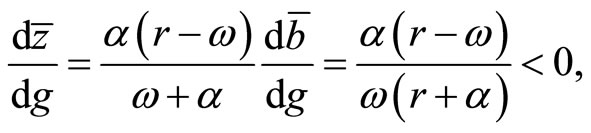 (25)
(25)
 (26)
(26)
This implies that an increase in 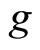 has negative effects on the steady-state values of consumption, real money balances, and net foreign assets.
has negative effects on the steady-state values of consumption, real money balances, and net foreign assets.
From Assumption 1, (10), (14), (24), and (25), the adjustment processes of  and
and 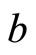 induced by an increase in
induced by an increase in 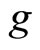 are the same results as in the literature (e.g., Mansoorian [10], Ikeda and Gombi [15]). An increase in fiscal spending leads
are the same results as in the literature (e.g., Mansoorian [10], Ikeda and Gombi [15]). An increase in fiscal spending leads  to fall less than its long-run level
to fall less than its long-run level  on impact, and to gradually decrease to
on impact, and to gradually decrease to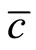 , which induces the current account deficit.
, which induces the current account deficit.
As shown in (26), an increase in 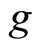 definitely reduces the steady-state real money balance
definitely reduces the steady-state real money balance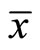 . From (12), the adjustment processes of
. From (12), the adjustment processes of 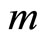 and the exchange rate depend on the intertemporal complementarity of preferences for real money balances as in the case of monetary policy depicted by Figure 1. We can summarize these results as the following proposition:
and the exchange rate depend on the intertemporal complementarity of preferences for real money balances as in the case of monetary policy depicted by Figure 1. We can summarize these results as the following proposition:
Proposition 2. Suppose that the government adopts the endogenous income-transfer regime. Then, under Assumption 1 with habit formation, in response to a permanent increase in fiscal spending1) on impact and in the long-run, real money balances decrease and hence the exchange rate depreciates; and 2) in transition, jointly with the current account deficits, exchange-rate depreciation (appreciation) takes place when liquidity preferences exhibit adjacent (distant) complementarity.
Proposition 2 shows that the dynamic relationship between the exchange rate and the current account depends crucially on the intertemporal complementarities of preferences for both consumption and money. Although preferences for consumption have been often reported to display adjacent complementarities, there is no empirical research on habit-forming behavior in money holdings. If the preferences exhibit adjacent complementarities, the instantaneous depreciation falls short of the long-run depreciation, so that the economy experiences interim currency depreciation with current account deficits. With distant complementarities for the liquidity preferences, an initial depreciation causes overshooting, which is followed by gradual appreciating process.
By using the endogenous time preference model, Obstfeld [1] shows that the same fiscal policy as in Proposition 2 causes current account surplus and currency appreciation in transition (see column (3)). Proposition 2 shows that the results of the monetary habit model, which could be empirically more relevant, totally differ from what he predicts.
4. Endogenous Fiscal Spending Regime
In this section let us consider the case of the endogenous fiscal spending regime, where lump-sum tax 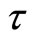 is constant and fiscal spending
is constant and fiscal spending  is determined so as to satisfy the government’s flow constraint (5). Substituting (5) into the balance-of-payment equation (13), we have:
is determined so as to satisfy the government’s flow constraint (5). Substituting (5) into the balance-of-payment equation (13), we have:
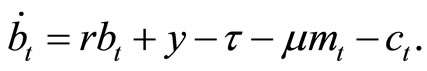 (27)
(27)
In contrast to the endogenous income transfer regime, the dynamics of real money balances and their habits do directly affect the balance-of-payment equation (27) in this regime, and therefore the dynamics of  are generated not only by consumption-habit capital
are generated not only by consumption-habit capital , but also by liquidity-habit capital
, but also by liquidity-habit capital . Using the same technique as in the previous section, the equilibrium dynamics of
. Using the same technique as in the previous section, the equilibrium dynamics of  are obtained as:
are obtained as:
 (28)
(28)
Figure 3 shows the phase diagram of consumptionand liquidity-habits on the 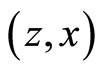 -space, where point
-space, where point 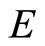 represents the steady-state point. The dynamics of the habit stocks
represents the steady-state point. The dynamics of the habit stocks 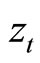 and
and 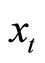 are generated by the autonomous Equations (7) and (11). Schedule
are generated by the autonomous Equations (7) and (11). Schedule 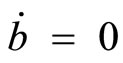 is a trajectory that is obtained by differentiating (28), substituting (7) and (11) into the result, and setting the result equal to zero:
is a trajectory that is obtained by differentiating (28), substituting (7) and (11) into the result, and setting the result equal to zero:

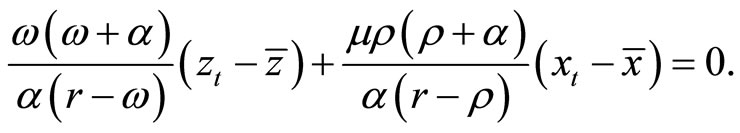
This depicts the set of  that makes the current account balanced. As shown in panel (a) of Figure 3, where preferences for real money balances display adjacent complementarity, the
that makes the current account balanced. As shown in panel (a) of Figure 3, where preferences for real money balances display adjacent complementarity, the 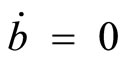 schedule is downward sloping, whose upper (lower) side exhibits current account deficit (surplus). This is because, with adjacent complementarity of preferences for consumption, a large habit stock z implies a high consumption level, which induces the current account deficits.
schedule is downward sloping, whose upper (lower) side exhibits current account deficit (surplus). This is because, with adjacent complementarity of preferences for consumption, a large habit stock z implies a high consumption level, which induces the current account deficits.
The consequence of the change in (27) and (28) alters the steady-state relationships (22) and (23) as follows:
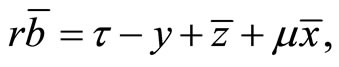 (29)
(29)
 (30)
(30)
The rest of the steady-state relationships (15) through (21) remains the same in this regime. The steady-state values of 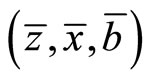 are jointly determined from (21), (29), and (30). Given
are jointly determined from (21), (29), and (30). Given , the other steady-state variables
, the other steady-state variables 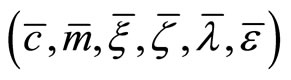 are determined by (15) through (20).
are determined by (15) through (20).
4.1. The Effect of Mixed Monetary Policy
In the endogenous fiscal spending regime, monetary policy such as a rise in  accompanies with the increase in fiscal spending
accompanies with the increase in fiscal spending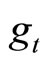 , therefore this mixed policy should have the combined effects of the monetary and
, therefore this mixed policy should have the combined effects of the monetary and
 (a)
(a)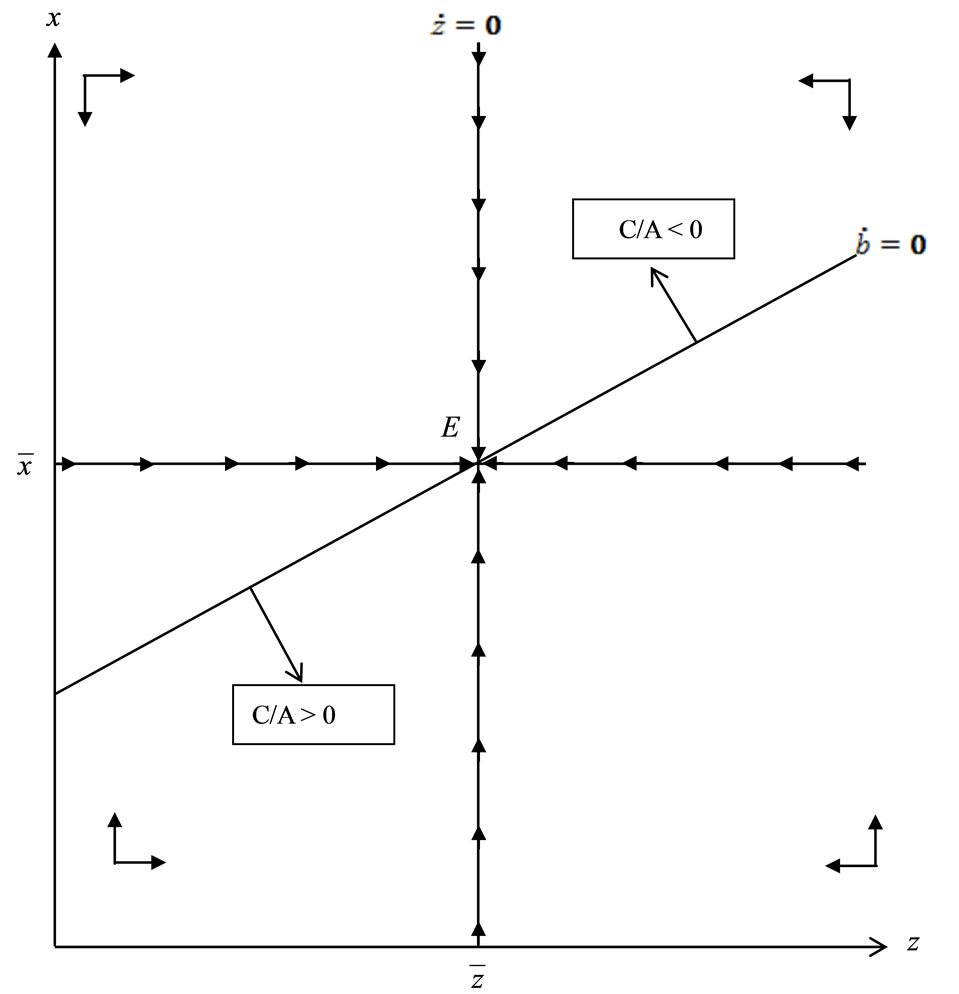 (b)
(b)
Figure 3. Phase diagram of money-habits x and consumption-habits z with the signs of the current account. (a) Adjacent complementarity: α + ρ > 0; (b) Distant complementarity: α + ρ < 0.
fiscal policy. Then, let us consider a once-and-for-all increase in . By differentiating (21), (29), and (30) with respect to
. By differentiating (21), (29), and (30) with respect to , the steady-state effects on
, the steady-state effects on  and
and  are obtained as:
are obtained as:
 (31)
(31)
 (32)
(32)
where:

which is positive under saddle-point stability.
The mixed monetary policy has two effects on the steady-state values of consumption-habit and liquidityhabit capitals : 1) an income effect, which is a negative effect caused by a decrease in real income owing to the increase in fiscal spending; and 2) a substitution effect, i.e., demand shifts from
: 1) an income effect, which is a negative effect caused by a decrease in real income owing to the increase in fiscal spending; and 2) a substitution effect, i.e., demand shifts from  toward
toward 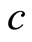 owing to the rise in
owing to the rise in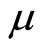 . In (31) and (32), the first terms, which are proportionate to the steady-state real money balance
. In (31) and (32), the first terms, which are proportionate to the steady-state real money balance , represent the income effect and the second terms represent the substitution effect. Both of the effects affect
, represent the income effect and the second terms represent the substitution effect. Both of the effects affect 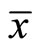 negatively, so that
negatively, so that 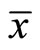 definitely decreases and hence the exchange rate depreciates on impact and in the longrun. The sign of the overall effect on
definitely decreases and hence the exchange rate depreciates on impact and in the longrun. The sign of the overall effect on 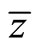 depends on the relative magnitudes of the negative income effect and the positive substitution effect.
depends on the relative magnitudes of the negative income effect and the positive substitution effect.
To examine the steady-state effect on external asset holdings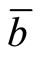 , we differentiate (29) by
, we differentiate (29) by 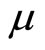 and substitute (31) and (32) into the result to obtain:
and substitute (31) and (32) into the result to obtain:
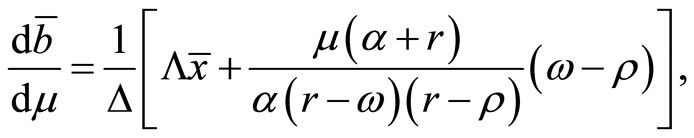 (33)
(33)
where:
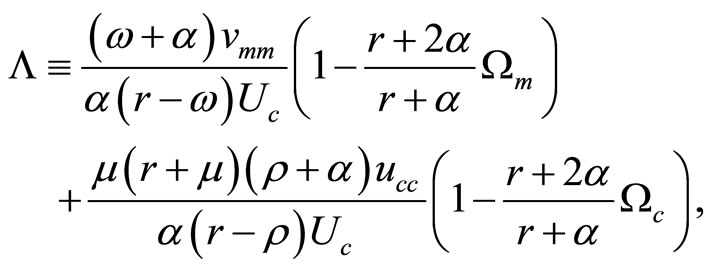
which is negative when preferences for real money balances exhibit adjacent complementarity or relatively weak distant complementarity, which can be dominated by the adjacent complementarity of preferences for consumption defined by Assumption 1.
In (33), the first term 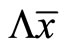 on the right-hand side represents the income effect on disposable net income
on the right-hand side represents the income effect on disposable net income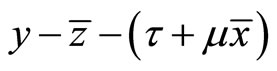 . The first term in the definition of
. The first term in the definition of  can be either negative or positive as preferences for real money balances display the adjacent or distant complementarity while the second term in
can be either negative or positive as preferences for real money balances display the adjacent or distant complementarity while the second term in  is negative from Assumption 1. In sum, the first term
is negative from Assumption 1. In sum, the first term 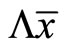 is negative unless the liquidity preference exhibits relatively strong distant complementarity. The second term of (33) represents the substitution effect on the net income, which is assumed to be positive since it seems quite natural that consumption is more habit forming than money holdings, i.e.,
is negative unless the liquidity preference exhibits relatively strong distant complementarity. The second term of (33) represents the substitution effect on the net income, which is assumed to be positive since it seems quite natural that consumption is more habit forming than money holdings, i.e., .
.
Although the sign of (33) is ambiguous, the larger the habit for real money balances is, the more likely it is to be negative. For example, when preferences for real money balances is of the type of adjacent complementarity 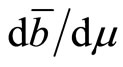 is necessarily negative. When the preferences display sufficiently strong distant complementarity,
is necessarily negative. When the preferences display sufficiently strong distant complementarity, 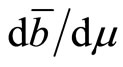 in turn takes positive sign.
in turn takes positive sign.
The effects of the mixed monetary policy can be summarized as the following proposition:
Proposition 3. With Assumption 1, suppose that a permanent increase in the growth rate of money in the endogenous fiscal spending regime takes place. Then:
1) real money balances decrease and hence the exchange rate depreciates, on impact and in the long-run;
2) exchange-rate depreciation (appreciation) takes place in transition when liquidity preferences exhibit adjacent (distant) complementarity; and3) the stronger the habit for real money balances is, the more likely the steady-state external assets are to decrease in response to the policy; In particular(a) 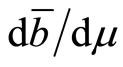 is negative when preferences for real money balances exhibit adjacent complementarity, and(b)
is negative when preferences for real money balances exhibit adjacent complementarity, and(b) 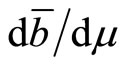 is positive when preferences for real money balances display sufficiently strong distant complementarity.
is positive when preferences for real money balances display sufficiently strong distant complementarity.
Proposition 3 implies that an increase in 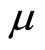 affects real money balances and hence the exchange rate just in the same way as in the endogenous income transfer regime, whereas the monetary policy is not surperneutral any more: induced changes in fiscal spending affect consumption and hence the current account. Note however that the effect on the current account dynamics differs from that of an increase in fiscal spending in the previous regime. Especially when liquidity preferences display sufficiently strong distant complementarity, the current account runs surplus even though preferences for consumption are assumed to be of adjacent complementarity.
affects real money balances and hence the exchange rate just in the same way as in the endogenous income transfer regime, whereas the monetary policy is not surperneutral any more: induced changes in fiscal spending affect consumption and hence the current account. Note however that the effect on the current account dynamics differs from that of an increase in fiscal spending in the previous regime. Especially when liquidity preferences display sufficiently strong distant complementarity, the current account runs surplus even though preferences for consumption are assumed to be of adjacent complementarity.
By setting 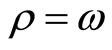 in (33), we obtain the following corollary:
in (33), we obtain the following corollary:
Corollary 1. Suppose that with Assumption 1, consumer preferences are weakly separable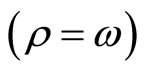 . Then, a permanent increase in the growth rate of money
. Then, a permanent increase in the growth rate of money 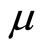 in the endogenous fiscal spending regime necessarily reduces the steady-state holding of net foreign assets
in the endogenous fiscal spending regime necessarily reduces the steady-state holding of net foreign assets .
.
Corollary 1 is consistent with the literature (e.g., Mansoorian [2]), in which a permanent increase in crawling pegged rate of exchange rate definitely reduces 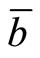 when preferences for homothetic consumption bundle of
when preferences for homothetic consumption bundle of 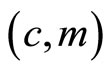 exhibit adjacent complementarity (as shown in column (4) of Table 1).
exhibit adjacent complementarity (as shown in column (4) of Table 1).
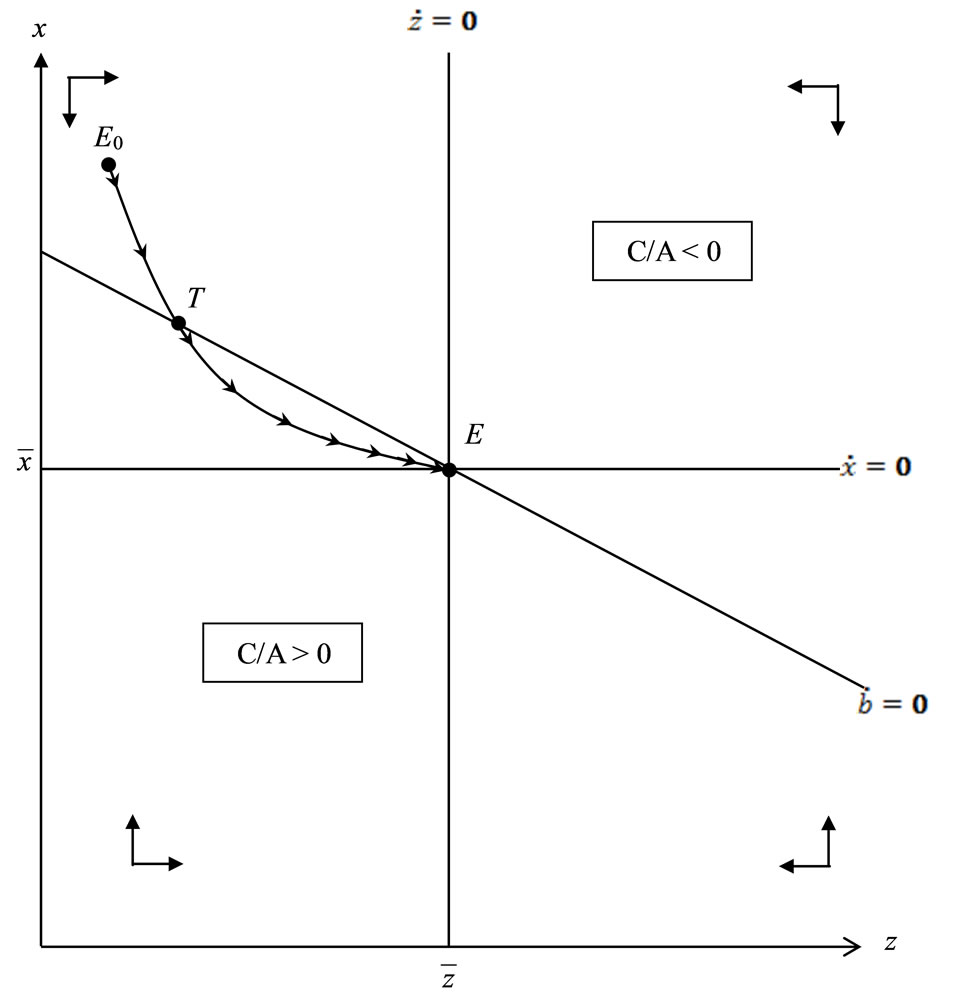
4.2. Transition: Possibilities of Non-Monotonic Dynamics
To examine the adjustment processes of the current account, especially focusing on the possibilities of nonmonotonic transition dynamics, we substitute (10) and (12) into (28) and differentiate the result by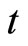 , and then obtain the following:
, and then obtain the following:
 (34)
(34)
This means that the current account 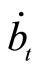 depends positively on the growth of consumption and of real money balances, where the individual dynamics of consumption and of real money balances are given by (10) and (12). As the adjustment speeds
depends positively on the growth of consumption and of real money balances, where the individual dynamics of consumption and of real money balances are given by (10) and (12). As the adjustment speeds  of
of 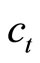 and
and 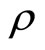 of
of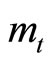 , respectively, generally differ, the current account can change its signs in the middle of transition if the signs of
, respectively, generally differ, the current account can change its signs in the middle of transition if the signs of 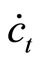 and
and 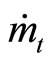 in transition are opposite.
in transition are opposite.
Two such cases of non-monotonic current account dynamics are illustrated in panels (a) and (b) of Figure 4 as the time profiles from the initial steady-state point 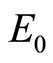 through the turning point
through the turning point 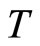 to the new steady-state point
to the new steady-state point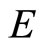 . In each panel, since adjacent complementarity of preferences for consumption means that consumption
. In each panel, since adjacent complementarity of preferences for consumption means that consumption 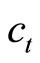 positively correlates with its habit
positively correlates with its habit , larger consumption habit
, larger consumption habit 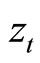 from the
from the 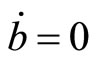 schedule implies higher consumption level than its steady-state level
schedule implies higher consumption level than its steady-state level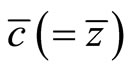 , thereby inducing the current account deficits in the right-hand side of the
, thereby inducing the current account deficits in the right-hand side of the 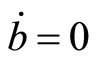 schedule.
schedule.
For the explanatory purpose, let us take only a case shown in panel (b), in which preferences for real money balances 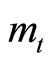 display distant complementarity, implying that
display distant complementarity, implying that 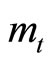 is negatively correlated with its habit capital
is negatively correlated with its habit capital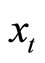 . A rise in
. A rise in 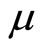 at
at 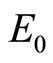 caused by the mixed monetary policy reduces
caused by the mixed monetary policy reduces , and then
, and then 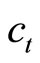 monotonically decreases over time:
monotonically decreases over time:  (shown as
(shown as 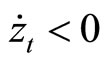 in the panel). On the other hand, the mixed policy definitely drops down
in the panel). On the other hand, the mixed policy definitely drops down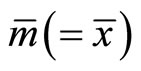 , and causing
, and causing , i.e., the opposite signs of
, i.e., the opposite signs of 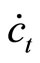 and
and 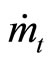 in entire transition with
in entire transition with  as shown in panel (b). Since consuming good is more habit forming than holding money balances in this case, the adjustment of
as shown in panel (b). Since consuming good is more habit forming than holding money balances in this case, the adjustment of 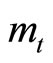 is more rapid than that of
is more rapid than that of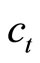 , i.e.,
, i.e., . The shock at point
. The shock at point  initially induces current account surplus because, on
initially induces current account surplus because, on 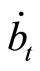 in (34), the effect of positive
in (34), the effect of positive  initially dominates the effect of negative
initially dominates the effect of negative . Since the dominant effect of
. Since the dominant effect of 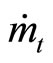 wanes faster than that of
wanes faster than that of  due to the difference in the adjustment speeds
due to the difference in the adjustment speeds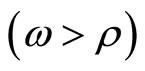 , the current account surplus lasts until the economy passes through the turning point
, the current account surplus lasts until the economy passes through the turning point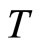 , where the countervailing effects of
, where the countervailing effects of 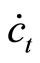 and
and  are totally offset on the
are totally offset on the 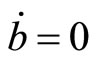 schedule, and thereafter turns to deficits as the negative effect of
schedule, and thereafter turns to deficits as the negative effect of 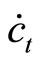 dominates the positive effect of
dominates the positive effect of  on
on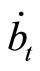 . The current account deficits continue until the economy arrives at the new steady-state levels at point
. The current account deficits continue until the economy arrives at the new steady-state levels at point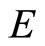 .
.
As is proved in Appendix C of [13], non-monotonic behavior of the current account does indeed take place if either the set of conditions (a1) through (a3) or the set of conditions from (b1) to (b3) in the following proposition holds valid:
Proposition 4. With Assumption 1, in response to a permanent increase in the growth rate of money in the endogenous fiscal spending regime, the current account can display non-monotonic dynamics. In particular, the following dynamic adjustments 1 and 2 can take place:
1) As illustrated in Figure 4(a), the current account runs deficits initially and then turns to surplus while the exchange rate depreciates in transition if the following three conditions are satisfied:
(a1) preferences for real money balances exhibit adjacent complementarity,  while consuming goods is more habit forming than holding money balances,
while consuming goods is more habit forming than holding money balances, ;
;
(a2) the steady-state effect on consumption is positive, ; and(a3) the steady-state effect on external asset holdings is negative,
; and(a3) the steady-state effect on external asset holdings is negative, .
.
2) As illustrated in Figure 4(b), the current account runs surplus initially and then turns to deficits while the exchange rate appreciates in transition if the following three conditions are met:
(b1) preferences for real money balances exhibit distant complementarity,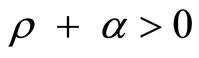 ;
;
(b2) the steady-state effect on consumption is negative,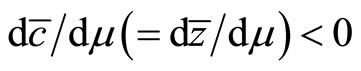 ; and(b3) the steady-state effect on external asset holdings is positive,
; and(b3) the steady-state effect on external asset holdings is positive,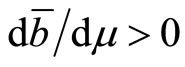 .
.
In the case of panel (a) (panel (b)), the initial current account deficits (surplus) dominates the latter current account surplus (deficits), which can be summarized as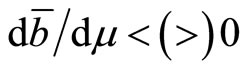 , as conditioned in (a3) (in (b3)).6
, as conditioned in (a3) (in (b3)).6
Note that the non-monotonic dynamics of current account 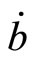 make unclear correlation between the exchange rate
make unclear correlation between the exchange rate 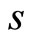 and the net foreign assets
and the net foreign assets 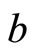 since the dynamics of
since the dynamics of  are always monotonic. This non-monotonic comovement of the exchange rate and the current account is one of theoretical counter-examples to the standard prediction that the exchange rate
are always monotonic. This non-monotonic comovement of the exchange rate and the current account is one of theoretical counter-examples to the standard prediction that the exchange rate  moves positively with the net foreign assets
moves positively with the net foreign assets 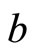 (e.g., Obstfeld [1], Obstfeld and Rogoff [16]).
(e.g., Obstfeld [1], Obstfeld and Rogoff [16]).
 (a)
(a)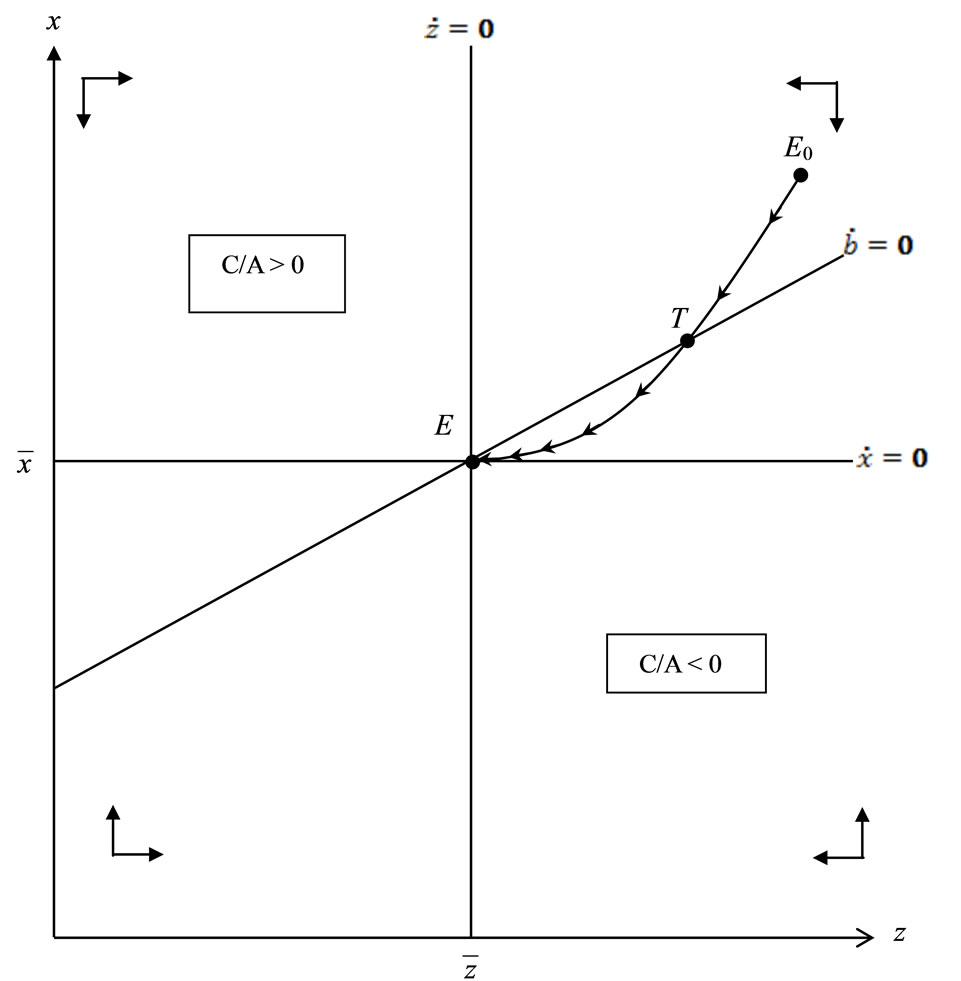 (b)
(b)
Figure 4. Possible non-monotonic transition paths of current account dynamics. (a) Adjacent complementarity: α + ρ > 0; (b) Distant complementarity: α + ρ < 0.
Note also that the independent habit forces over consumption and money play the critical role in generating non-monotonic dynamics of the current account. This mechanism differs from that in the existing literature discussing on non-monotonic current account dynamics: Shi and Epstein [4] incorporate habit formation and endogenous discounting; and Mansoorian and Neaime [3] focus on habits and durability. Our model proposes a new specification to describe empirically plausible nonmonotonicity of the current account dynamics.
5. Conclusions
Incorporating habits over consumption and over real money balances into a small country model, we have examined the dynamic adjustment of the current account and the exchange rate to monetary and fiscal policies in two alternative policy regimes: (1) the endogenous income transfer regime; and (2) the endogenous fiscal spending regime. In response to the policies under either regime, the exchange rate definitely depreciates on impact and in the long run whereas the exchange rate depreciates (appreciates) in transition if preferences for real money balances exhibit adjacent (distant) complementarity. In regime (2), the habits over consumption and real money balances jointly generate possibly non-monotonic current account dynamics, and an induced increase in fiscal spending can cause current account surplus under strong distant complementarity of real money balances.
As a possible direction for future research, it would be interesting to extend our mutually independent consumptionand money-habits model to a two-country framework as developed by Ikeda and Gombi [17] so as to contribute to producing richer implications for the movements of the current account and the exchange rate.
6. Acknowledgements
The authors are grateful for the helpful comments on the earlier versions circulated as [13] to Y. Ono, T. Ogawa, and the participants of the Osaka University Global COE Conference of the Economic Analysis for Time-Preference and Economic Dynamics (Matsuyama, Japan), the 72nd International Atlantic Economic Conference (Istanbul, Turkey), and the Asset Pricing Research Workshop (Osaka, Japan). They also appreciate financial supports to Gombi from the faculty research fund from 2011 to 2013 of Ritsumeikan University, and to Ikeda from Grants-in-Aid for Scientific Research (B No. 21330046) from the Japan Society for the Promotion of Science and the 21st COE Program and the Joint Usage/Research Center Project of ISER from the Ministry of Education, Culture, Sports, Science and Technology. In addition, Gombi gratitudes for facilitative supports from the School of Economics and Finance, the Collage of Business, Massey University during his sabbatical stay at Palmerston North, New Zealand as a visiting research fellow.
REFERENCES
- M. Obstfeld, “Macroeconomic Policy, Exchange-Rate Dynamics, and Optimal Asset Accumulation,” Journal of Political Economy, Vol. 89, No. 6, 1981, pp. 1142-1161. doi:10.1086/261026
- A. Mansoorian, “On the Macroeconomic Policy Implications of Habit Persistence,” Journal of Money, Credit, and Banking, Vol. 28, No. 1, 1996, pp. 119-129. doi:10.2307/2077970
- A. Mansoorian and S. Neaime, “Durable Goods, Habits, Time Preference, and Exchange Rates,” The North American Journal of Economics and Finance, Vol. 14, No. 1, 2003, pp. 115-130. doi:10.1016/S1062-9408(02)00115-8
- S. Shi, “Weakly Nonseparable Preference and Distortionary Taxes in a Small Open Economy,” International Economic Review, Vol. 35, 1994, pp. 411-428. doi:10.2307/2527061
- S. Ikeda, “Exportand Import-Specific Habit Formation,” Review of Development Economics, Vol. 13, No. 4, 2009, pp. 709-718. doi:10.1111/j.1467-9361.2009.00525.x
- G. Constantinides, “Habit Formation: A Resolution of the Equity Premium Puzzle,” Journal of Political Economy, Vol. 98, No. 3, 1990, pp. 519-543. doi:10.1086/261693
- J. Y. Campbell and J. H. Cochrane, “By Force of Habit: A Consumption-Based Explanation of Aggregate Stock Market Behavior,” Journal of Political Economy, Vol. 107, No. 2, 1999, pp. 205-251. doi:10.1086/250059
- C. D. Carroll, J. Overland and D. N. Weil, “Saving and Growth with Habit Formation,” American Economic Review, Vol. 90, No. 3, 2000, pp. 341-355. doi:10.1257/aer.90.3.341
- A. Daz, J. Pijoan-Mas and J. Ros-Rull, “Precautionary Savings and Wealth Distribution under Habit Formation Preferences,” Journal of Monetary Economics, Vol. 50, No. 6, 2003, pp. 1257-1291. doi:10.1016/S0304-3932(03)00078-3
- A. Mansoorian, “Habit Persistence and the HarbergerLaursen-Metzler Effect in an Infinite Horizon Model,” Journal of International Economics, Vol. 34, No. 1-2, 1993, pp. 153-166. doi:10.1016/0022-1996(93)90071-5
- S. Shi and L. G. Epstein, “Habits and Time Preference,” International Economic Review, Vol. 34, No. 1, 1993, pp. 61-84. doi:10.2307/2526950
- H. E. Ryder and G. M. Heal, “Optimal Growth with Intertemporally Dependent Preference,” Review of Economic Studies, Vol. 40, No. 1, 1973, pp. 1-33. doi:10.2307/2296736
- I. Gombi and S. Ikeda, “Macroeconomic Policy, Current Accounts, and Exchange Rate Dynamics with Habit Formation,” Unpublished (Available upon Request), 2012.
- J. W. Gruber, “A Present Value Test of Habits and the Current Account,” Journal of Monetary Economics, Vol. 51, No. 7, 2004, pp. 1495-1507. doi:10.1016/j.jmoneco.2003.12.004
- S. Ikeda and I. Gombi, “Habits, Costly Investment, and Current Account Dynamics,” Journal of International Economics, Vol. 49, No. 2, 1999, pp. 363-384. doi:10.1016/S0022-1996(98)00067-1
- M. Obstfeld and K. Rogoff, “Foundations of International Macroeconomics,” MIT Press, Cambridge Mass, 1996.
- S. Ikeda and I. Gombi, “Habit Formation in an Interdependent World Economy,” Macroeconomic Dynamics, Vol. 13, No. 4, 2009, pp. 477-492. doi:10.1017/S1365100509080183
NOTES
*Corresponding author.
1For weakly non-separable preferences, see Shi [4]. Also see Ikeda [5] for the application of weakly non-separable preferences to a habit model.
2It is quite natural to think that each good and service has a different degree of habit strength. For example, so called habitual goods like tobacco and alcohol show strong degrees of habit. Playing video games can be thought as one of habitual services especially for kids. Therefore, we think that liquidity service has somewhat different degree of habit strength from consuming goods.
3There are empirical evidences to that consumption habits are of the type of adjacent complementarity (e.g., Constantinides [6]; Campbell and Cochrane [7]; Carroll et al. [8]; and Diaz et al. [9]).
4For detailed derivations of the analytical results in the paper, see Gombi and Ikeda [13], which is available upon request.
5This is because 1) domestic money is internationally non-traded asset, 2) felicity functions u(c, z) and v(m, x) are specified as additively separable, and 3) the income transfer the representative agents to perfectly compensates the inflation tax induced by an increase in μ in the non-distortionary way.
6An applied econometrician could easily identify these two cases by observing the relation of the opposite signs between dynamics of 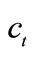 and those of
and those of 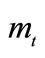 in transition:
in transition: 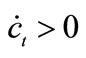 and
and 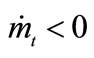 in the case of panel (a) whereas
in the case of panel (a) whereas 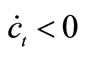 and
and 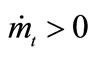 in the case of (b).
in the case of (b).

