Journal of Biophysical Chemistry
Vol.4 No.2(2013), Article ID:31764,6 pages DOI:10.4236/jbpc.2013.42007
Spin nature of genetic code
![]()
1School of Physics and Astronomy, University of Manchester, Manchester, UK
2Faculty of Biology and Soil, Saint-Petersburg State University, Saint Petersburg, Russia
email: atulub@yahoo.co.uk
Copyright © 2013 Alexander A. Tulub, Vassily E. Stefanov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 25 January 2013; revised 27 February 2013; accepted 9 March 2013
Keywords: Spintronics; Nucleotides; Genetic Code; Quantum Computations; Berry’s Phase; Hyperfine Coupling
ABSTRACT
Nature has developed codon as a tool to manipulate a two-electron spin symmetry (short-living electrons, forming a radical pair, arise from the Mg-bound nucleosidetriphosphate cleavage at the triplet/singlet (T/S) crossing), which permits or forbids further nucleotide synthesis (DNA/RNA) and the synthesis of proteins. The thesis is confirmed by conducting DFT:B3LYP (6- 311G** basis set) computations (T/S potential energy surfaces) with the model system composed of the template (C-G-C-G-A nucleotide sequence) and the growing chain (G-C-G nucleotide sequence, DNA or RNA). The origin of codon is in hyperfine interaction between a single electron, transferred onto the template, and three 31P nuclei built into the phosphorus fragments of nucleotides. The nuclei, together with the polynucleotide structure, form a spiral twist that is homeomorphic to a triangle patch on the Poincare sphere. Each triangle has unique angle values depending on the nucleotide nature and their position in the codon. The patch tracing produces the Berry phase changing the electron spin orientation from “up” to “down”. The Berry phase accumulation proceeds around the (T/S) conical intersections (CIs). The CIs are a result of complementary recognition between nucleotide bases at distances exceeding the commonly accepted Watson-Crick pairing by 0.17 A. Upon changing spin symmetry, the DNA or RNA chain is allowed to elongate by attaching a newly coming nucleotide. Without complementary recognition between the bases, the chain stops its elongation. The Berry phase accumulation along the patch tracing explains the effect of Crick’s wobbling when the second nucleotide plays a primary role in recognition. The data is directly linked to cre- ation of a quantum computing device.
1. INTRODUCTION
As our understanding of DNA structure is practically complete, the molecule; however, remains a total mystery [1]. This is notably true when we try to find answers to the physical nature of DNA operation and the origin of genetic code. The latter is proved to be triplet [2]. However, it is very unlikely that anyone today is able to explain why it is triplet, including the effect of wobbling, when the second nucleotide plays a primary role in recognition [3]. The paper aims to shed light on why genetic code is triplet. The answer is rooted in recently found short-living spin nature of nucleotides [4,5].
2. MODELING
In living cells DNA/RNA chain growing proceeds on its complementary template (actually, with the help of DNA/RNA polymerase [6]; the latter is not included into computations because of its complexity) and assumes the Mg-induced nucleosidetriphosphate (NTP; N = G, A. C, T, U) decay to nucleosidemonophosphate (NMP) [6]. The Mg-NTP decay is spin-dependent [4]. It occurs at the conical intersection (CI) of the triplet (T) and singlet (S) potential energy surfaces (PESs) and assumes overcoming a potential barrier of 25.4 kcal/mol [4,5]. The CI passage produces a radical pair (RP)—·NMP and ·OH (· stands for a radical)—which spin correlation determines the further elongation of the chain or termination of its growth. With the RP and its two spins in mind, we have a picture (Figure 1) that models the process of DNA/RNA nucleotide synthesis on the complementary DNA template and proves the necessity of a triplet nucleotide se-
 (a)
(a) (b)
(b)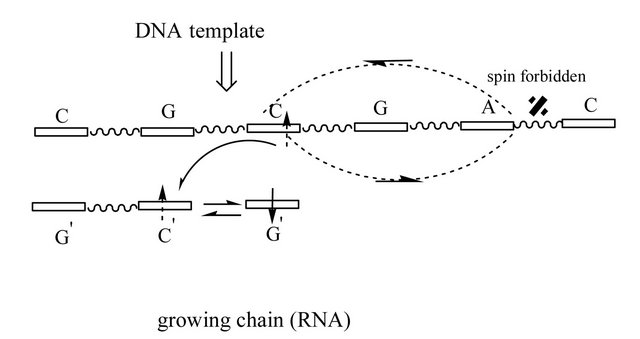 (c)
(c)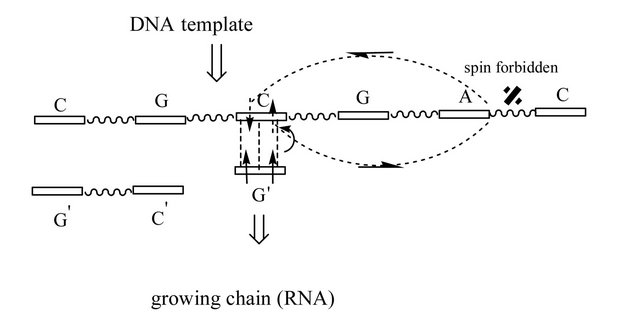 (d)
(d)
Figure 1. Model structure of the nucleotide growing chain (DNA/RNA) on the DNA template; (a) and (b) structures correspond to DNA, (c) and (d)—to RNA. G’ (growing chain) and C (template) are connected by weak H-bonds—dashed lines (the initial recognition process between the complementary nucleotides; details see in text); the rest nucleotides are H-bonded (W-C distances ((a) and (b)) or non-bonded ((c) and (d)). The initially created RP is in T state (two arrows, indicating spins, are up-directed) and their spins, for simplicity, rest on the G’ nucleotide (actually, the spins are on ·G’MP and ·OH, see text and [4]). One electron spin migrates on the template (a small curved arrow). The two curved arrows covering the C-G-A nucleotides indicate a closed path on the Poincare sphere (Figure 3). After tracing the path, the spin flip occurs, which corresponds to accumulating a Berry phase g = p. Energetically, it favors the electron transfer back onto the growing chain ((b) and (d)), particularly onto the C’ nucleotide (chemically, it launches the production of the water molecule and the ·C’ nucleotide with the oppositely directed spin to that on ·G’MP, details in [4]). Any RP, in our case this is ·C’ and ·G’MP, with up and down spins, prefers to recombine, which results in production of the diester bond between C’ and G’ (back and forth arrows). The difference between DNA and RNA nucleotide polymerization is that the first makes G’ and C closer as the second separates G’ and C. Diester bonds are indicated with wave lines.
quence (codon).
The C and G nucleotides of the template are complementary bonded to the G’ and C’ nucleotides—the DNA growing chain, Figure 1(a) (hereinafter, the upper bars indicate nucleotides of the growing chain). If G’ and C’ are RNA nucleotides, H-bonds are not formed; the named nucleotides are separated from their counterparts by 2.38 A [7]. The rest nucleotides (C, G, A, C) of the template are not bonded unless the first C nucleotide, see below. The adjoining G’ nucleotide (the growing chain) is a radical ·G’MP (DNA or RNA nucleotide). Its geometry was found previously together with the geometry of the ·OH-HO-C3-sugar fragment attached to the C’ nucleotide (left) [4]. The G’ nucleotide forms three complementary H-bonds with the C nucleotide of the template. The initial distances, however, are 0.17 A longer than those in the classical Watson-Crick (W-C) pairing (in Figures 1(a) and (c)) this is shown by a displacement of G’ compared to C’, up and down, respectively) that makes H-bonding highly weak. The outlined structure (together with further structural geometries) is a result of carrying out DFT:B3LYP (6-311G** basis set; New York Blue Gene/L supercomputer complex, NYCCS) computations (T and S states) in search of conical intersections (CI) and in finding the energy minima in the [T1,T2] region—0.05 A displacements of freely making/breaking-bond atoms (H-bonds, decomposed G’TP products, water molecules) [8]. The core atoms (nucleotide bases, sugars, diester bonds of the linked nucleotides) were fixed to make computations less timeand resource-consuming. The structure is surrounded by the water environment of 87 water molecules on the periphery of the hydrophilic parts (double water shell). The found structures (Figures 1(a) and (c)) were considered as initial ones in the [T1,T2] region. The hyperfine coupling (hfc) between a free electron of the RP (see below) and magnetic nuclei—31P nuclei showing 100% natural abundance [9] and large hfc [10,11]—was included in the vicinity of the T1 and T2 (T/S) crossings (Figure 2). Including the hyperfine coupling slows computations significantly but, as we shall see, its presence is absolutely vital for our purposes— specifically, when the electron is able to change its spin polarization upon the influence of hfc. Outside the [T1,T2] region, Figure 2, the same DFT:B3LYP method was used. The only distinction was in not including the hyperfine interaction as the DNA/RNA systems outside T1 and T2 do not “feel” its presence.
3. RESULTS AND DISCUSSION
The G’TP (DNA/RNA) decay upon acting the Mgcofactor (T/S crossing) results in producing two electrons, which are formally placed on the G’ nucleotide, Figures 1(a) and (c) (actually, this is a ·G’MP and ·OH-HO-sugar-C’ complex, surrounded by a water shell of 18 water molecules [4], that makes a single ensemble). Totally, the two electrons form a T radical pair. The T* point might formally be assigned to the local minimum in the [T1,T2] region, see below. T* is distanced from T1 (DNA) or T2 (RNA) by D = 0.62 kcal/mol—the value, which nearly identical to vibration energy of hydrogen atoms (the energy of stretching modes [12]). It is worth recalling that the H-bonding energy in the true Watson-Crick G-C pair is ~12 kcal/mol (DFT computations [13]).
Since the RP is in T state, one of the RP electrons migrates onto the template (the C nucleotide) to make the distance between the electrons as large as possible (Pauli exclusion principle) [14], Figure 1. The process occurs thanks to the T PES (the upper part in Figure 2), which reveals the left or right tilt depending on what sort of nucleotide we have—DNA or RNA. The tilts arise immediately after switching on the H-bonds in computations (if H-bonds are not switched on, the tilts never arise; this, for instance, is the case when the nucleotide bases are not complementary). Switching on H-bonds shifts the local minima to T1/T2 (DNA or RNA) and prevents the system from coming back to T*. Figuratively, T* acts as a “molecular clairvoyant” pointing out which way the nucleotide, depending on its nature, to go-left (DNA), right (RNA), or stay where it is (non-complementary nucleotide bases). Without being complementary bonded, small vibrations make the T* state globally unstable (any Tstate in biological systems is normally unstable) that stops nucleotide chain lengthening and finally removes the “unlucky” nucleotide because the latter is unable to form a diester bond. The H-bonding, on the contrary, directs the nucleotides to T1 or T2, determining further nucleotide bonding, see below. The electron transfer on the template (the H-bonds are switched on) might be viewed as a proton-coupled transfer [15] when protons assist the electron migration through stretching proton vibration modes in the G’-C pair. The electron migration separates the RP electrons making them occupy two different strands—the analogue of what we have in quantum wires if the initial state is T [14].
The spin of the migrated electron “reads” three nucleotides on the right. To answer why that is happening one can have in mind at least three things. First, when we speak about spin, it assumes the presence of a magnetic field that allows us to “see” the spin. DNA or RNA in living cells has no external magnetic field (Earth’s natural magnetic field is highly low, ~5 G, to initiate biochemical processes [16]), but has the internal field, B [16]. The latter originates mostly from the hyperfine coupling (B = Bhfc = I A S, where I and S are nuclear and electron spin operators, and A is the hfc tensor [17]), which in phosphorus-containing systems can reach the level of weak Zeeman fields [18,19]. In organic radicals like ours it is common to neglect the spin-orbit coupling
(a)

(b)
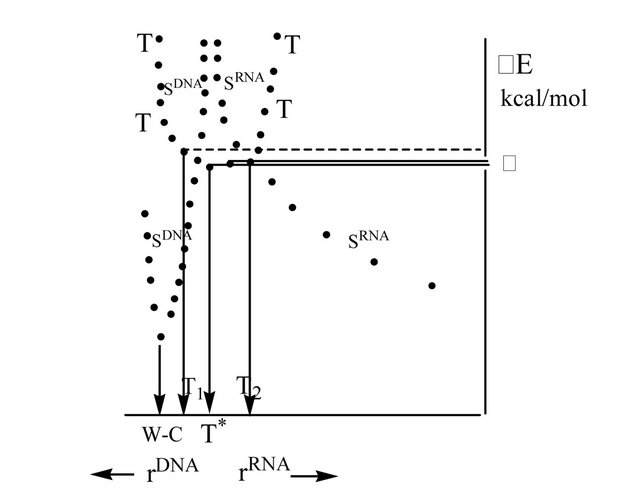
Figure 2. Potential energy surface cuts of T and SDNA and SRNA. In the upper part of the picture T surface crosses S surfaces—T1 and T2 points—which become the minima in case of DNA/RNA growing chain ((a) and (b)); D is the energy difference between T* and T1/T2, see text. W-C point corresponds to the energy minimum in case of DNA (the growing chain and the template are W-C distanced); T* point indicates the local energy minimum in case of non-complementary nucleotide pairs.
SOC [17]. Mathematically, it means that the effective spin Hamiltonian becomes a real electron spin of the paramagnetic molecule with a definitely computed sign along x, y, and z coordinates. Physically, the neglect of SOC in RP systems composed of light atoms comes from the fact that the electron orbital angular momentum of the unpaired electron is practically quenched. Second, the B vector is highly dependent on the nucleotide-nucleotide space curvature-gauge field [20] (or gauge potential A, using the language of the gauge field theory [21]). Third, the presence of A creates a geometric phase on a curved manifold (twist structures, nested structures etc.) known today as Berry’s phase [22,23].
When one of the electrons migrates onto the template (see above), its spin “feels” the hfc effect emerging from three 31P nuclei. This happens because the template has a right-hand twist sequentially, domain after domain (each of three nucleotides), blocking the hfc effect between the free electron and the phosphorus atoms (as we shall see the effect is directly linked to the value cosf)—the gauge field flux associated in our case with B [24,25]. The twist cannot be changed, say to the left twist (the nature will not allow it), or exceed the value of π/2 (a polar angle, q), Figure 3 [26,27]. The latter comes from the fact that the quantum computations proceed in the Hilbert space assuming the presence of a projection operator on this very space, up to the wave function phase, f. The said fact limits the value q Î [0, π/2 on the projection space (surface g over C manifold around T1 or T2, Figure 4), but does not restrict the value of the gauge field flux through the contours g, f, e etc., Figure 4, in the bundle space (for the purpose of clarity, we deliberately restrict ourselves with three bundle layers), which is determined by q and the azimuth angle, j Î [0, π]. Topologically, the picture identifies the hfc interaction with the electron spin “motion” on the Poincare sphere [24,25] having a triangle patch, Figure 3, with unique phase values fi, Figure 4. The triangle connects three points centered on the 31P atoms of the template, Figure 3. The general formulae for Berry’s phase picturing a spin motion on such a Poincare sphere is γ = π (1 − cosS03f). Because of the evident fact that γ cannot accumulate its topological charge (the Chern number is confined from above [25]), the Berry phase has to be flagged, γ = [0, π], Figure 3. The first flag corresponds to the electron migration onto the template (no phase, cosf0 = 1), the last flag corresponds to the electron spin “motion” to the third nucleotide. The phase γ reaches its maximum each time upon tracing the patch: γ = π, cosSf0 = 0). The last flag, among other things, does not allow the topological charge to change its sign. That particularly explains why the electron spin “jump” from A to C nucleotide on the template is forbidden, Figure 1.
As we just said, each patch is unique. It assumes that the values fι can basically be different. Thus, if f exceeds π/6, then cosf2 prevails, because upon summation over i the value cosf2 becomes defining. Physically, the situation corresponds to that when the second nucleotide in a three-nucleotide sequence becomes defining (the effect of wobbling [3], e curve, Figure 4)) and the third nucleotide becomes irrelevant (the genetic code is degenerate [6]). Figure 4 shows different values of the Berry phase accumulation within the closed interval γ Î [0, π]. If f equals to π/6 (f curve, Figure 4), the contribution of each nucleotide is valuable (the situation when all the nucleotides are “weak”, like in case of a three-A nucleotide sequence [6]).
The closure of the C path produces the electron spin flip, γ = π. The energy gain of the spin flip, according to our computations (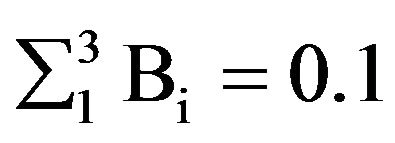 T, summation is over the
T, summation is over the


Figure 3. (a) Poincare sphere with a triangle patch corresponding to closure of the path C. Geometrically, the picture is homeomorphic to the hyperfine interaction understood as the electron spin scattering on three 31P atoms (vertices of the triangle). The tangent vector (the analogue of A) along the path experiences change in its orientation limited by the Berry phase interval g Î [0, π]; (b) is the isomorphic right-handed motion of the electron spin in space (details see in text).
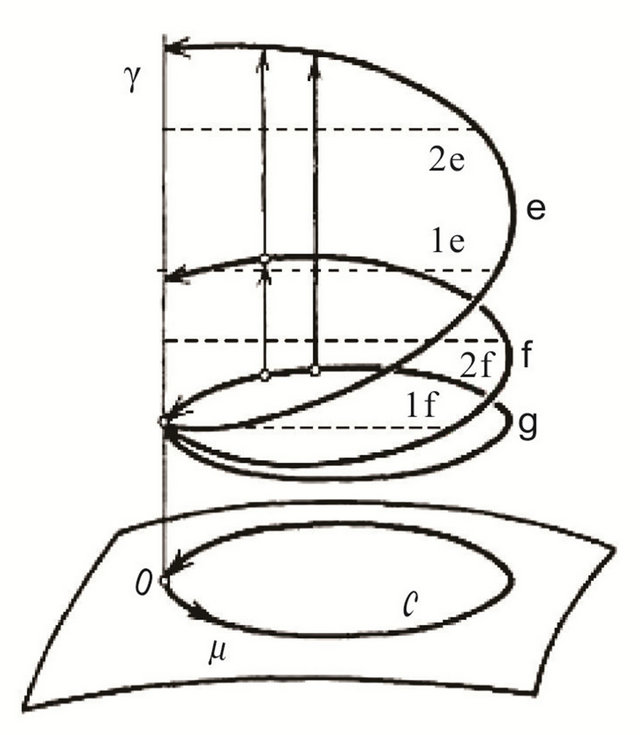
Figure 4. Visualization of the bundle space formation (g, f, e, etc.) over the closed loop C on the Poincare sphere (the base) with a parameter μ (in our case it is associated with the direction of the path tracing). g is the projection of C onto the Hilbert space of U(1) symmetry; f is the first bundle layer with f = π/6; e is the second bundle layer with f > π/6; γ is the Berry phase covering the bundle space. Dashed lines correspond to projection of f on γ.
magnetic fields from three nucleotides) is 0.02 cm−1. The T1 (DNA) and T2 (RNA) points undergo symmetry change from T to S (T/S crossing), Figure 2. This, in turn, provokes the electron back transfer onto the growing chain. The RP now is in S state. This immediately launches the RP recombination that proceeds through the Mg-assisted homolytic O-H bond break (the sugar-C3-O-H fragment of the C’ nucleotide). The ·H transfer onto the ·OH radical forms the water molecule. As a result, instead of the ·OH radical we have the ·C’ radical—correctly speaking, the C’-sugar-O· radical. The two radicals, ·C’ and ·G’MP, with oppositely directed spins recombine through making the diester bond [6]. The details of the outlined process might be found in [4].
It has to be stressed that the spin back transfer (T®S) shifts the G’ nucleotide up (DNA, Figure 1(b)) or down (RNA, Figure 1 (d)) so that the growing chain and G’ become leveled relative to the distance between the growing chain and the template. This facilitates formation of the diester bond. Both processes assume going along the SDNA or SRNA PESs in the direction of lowing the value of total energy E, Figure 2. If T1/T2 are chosen as reference points (DE = 0), DEW-C(DNA) = − 25.6 kcal/mol (diester bond making plus W-C bond making). When compared with the energy barrier (see Section II) for the Mg-G’TP (the initial stage of the system), one can see that the energy gain upon the chain elongation is negligibly small. The effect is not surprising—it just confirms the idea that highly complex biochemical reactions in living cells produce very small energy, leaving biological systems thermodynamically stable. The DNA global minima, DEW-C(DNA), and the T state are separated by a huge energy ~4.6 eV (the T curve goes sharply upward, Figure 2). The result fully agrees with the previously published data [28]. In case of RNA, the diester binding energy gain is ~12.3 kcal/mol. Without the confinement by RNA polymerase (in our case it was initially reached by fixing the distance between the growing chain and the template), RNA and the template show separation leading to decrease in the total energy (SRNA curve, Figure 2). This result is widely known in cell biology—DNA and RNA single strands “do not like each other” [6].
4. CONCLUDING REMARKS
In conclusion, a few remarks are required to generalize what is codon and how it operates.
1) Topologically, each codon might be considered as a single layer of the bundle space covering all the DNA/ RNA chain length.
2) The codon acts as the electron spin flip generator (at the ends of the loop closure), which initiates (the phase g = p; S state) or prevents (the phase g = 0; T state) further molecular synthesis, including amino acid synthesis.
3) The non-integrable Berry phase, associated with B (space curvature), allows us to work with phases, which fully describes the gauge fields (various magnetic fields). Together, at the imaginary time point [29], they produce the invariant e(g = p) = 23, corresponding to the number of possible amino acids that DNA encodes (commonly the number is reduced to “20” that is identical to e3 = 20 if p is replaced by its closest integer number “3”). Chemically and biologically, we are unable to deal with a noninteger number of molecules.
4) When dealt with phases, it assumes the interference effects of all possible electron trajectories (in first approximation, this corresponds to the electron scattering on nuclei 31P) with non-zero values of A. When such a nucleotide-string device constructed, one can speak about performing quantum computations with a non-integer basis (number e, raised to variable powers (phases)).
5) Any attempts to “see” phase operation in DNA with true W-C distances are doomed to failure. The fact is that, first, DNA has no free electrons (they emerge locally and they are short-lived) and, second, the energy between complementary strings hugely exceeds the energy of hyperfine coupling, which is “not seen” except the CIs.
REFERENCES
- Chou, K.C., Endres, R.G., Cox, D.L. and Singh, R.R.P. (2004) The quest to high-conductance DNA. Review of Modern Physics, 76, 195-214. doi:10.1103/RevModPhys.76.195
- Crick, F. (1988) Chapter 8: The genetic code. What mad pursuit: A personal view of scientific discovery. Basic Books, New York.
- Crick (1966) Codon-anticodon pairing: The wobble hypothesis. Journal of Molecular Biology, 19, 548-555.
- Tulub, A.A. (2011). Spin effects govern DNA/RNA nucleotide polymerization. Journal of Biophysical Chemistry, 2, 300-309. doi:10.4236/jbpc.2011.23034
- Tulub, A.A. (2008) Mg spin affects adenosinetriphosphate activity. PMC. Physics B, 1, 18. doi:10.1186/1754-0429-1-18
- Berg, J.M., Tymoczko, J.L. and Stryer, L. (2002) Biochemistry. 5th Edition. W. H. Freeman Publishing, New York.
- Korkhin, Y.U., Unligil, O., Littlefield, P., Nelson, D., Stuart, P., Sigler, S. and Abrescia, N. (2009) Evolution of complex RNA polymerases: The complete archaeal RNA polymerase structure. PLoS Biology, 7, 102-128. doi:10.1371/journal.pbio.1000102
- Haas, Y. and Zilberg S. (2004). The use of elementary reaction coordinates in the search of conical intersections. In: Worth, G.A. and Althorpe, S.C., Eds., Quantum dynamics and conical intersections, CCPG Publishing, 145- 187.
- Cvade-Menum, B.J. (2003) Using phosphorus-31 nuclear magnetic resonance spectroscopy to characterize organic phosphorus in environmental samples (Chapter 2). In: B.L. Turner, E. Frossard and D.S. Baldwin, Eds., Organic phosphorus in the environment, CABI Pibl, London, 21- 45.
- Koptyug, I.V., Sluggett, G.W., Ghatlia, N.D., Landis, M.S., Turro, N.J., Ganapathy, S. and Bentrude, W.G. (1996) Magnetic field dependence of the 31P CIDNP in the photolysis of a benzyl phosphite. Evidence for a T-S mechanism. Journal of Physical Chemistry, 100, 14581-14583. doi:10.1021/jp9619705
- Jockusch, S. and Turro, N.J. (1998) Phosphinoyl Radicals: Structure and Reactivity. A Laser Flash Photolysis and Time-Resolved ESR Investigation. Journal of American Chemical Society, 120, 11773-11777. doi:10.1021/ja982463z
- Saenger, W. (1984) Principles of nuclear acid structures. Springer Verlag, New York.
- Preuss, M., Schmidt, W.G., Seino, K., Ller, J.F. and Bechstedt, F. (2003) Groundand excited-state properties of DNA base molecules from plane-wave calculations using ultrasoft pseudopotentials. Journal of Computing Chemistry, 25, 112-122. doi:10.1002/jcc.10372
- Žutić, I. and Das Sarma, S. (2004) Spintronics: Fundamentals and applications. Reviews of Modern Physics, 76, 323-357. doi:10.1103/RevModPhys.76.323
- Hammes-Schiffer, S. and Soudackov, A.V. (2008) Proton-coupled electron transfer in solution, proteins, and electrochemistry. Journal of Physical Chemistry B, 112, 14108-14116. doi:10.1021/jp805876e
- Kahn, O. (1993) Molecular magnetism. VCH Publishers Inc., New York.
- van Lenthe, E., Ad van der, A. and Wormer, P.E.S. (1998) Density functional calculations of molecular hyperfine interactions in the zero order regular approximation for relativistic effects. Journal of Chemical Physics, 108, 4783- 4796. doi:10.1063/1.475889
- Turro, N.J. (1991) Modern molecular photochemistry. University Science Books.
- Koptyug, I.V., Sluggett, G.W., Ghatlia, N.D., Landis, M.S., Turro, N.J., Ganapathy, S. and Bentrude, W.G., (1996) Magnetic Field Dependence of the 31P CIDNP in the Photolysis of a Benzyl Phosphite. Evidence for a T-S Mechanism. Journal of Chemical Physics, 100, 14581-14583. doi:10.1021/jp9619705
- Schutz, B.F. (1982) Geometrical methods of mathematiccal physics. London.
- Bachman, D. (2010) A geometric approach to differential forms. California Polytech. State University Publishers, San Luis Obispo.
- Reta, R. (2000) Manifistation of Berry’s phase in molecules and condensed matter. Journal of Physics-Condensed Matter, 12, 107-143. doi:10.1088/0953-8984/12/9/201
- Berry, M.V. (1984) Quantal phase factors accompanying adiabatic changes. Proceedings of the Royal Society of London Series A, 392, 45-57.
- Rojo, A.G. and Bloch, A.M. (2010) The rolling sphere, the quantum spin, and a simple view of the Landau-Zener problem. American Journal of Physics, 78, 1014-1024. doi:10.1119/1.3456565
- Mangiarotti, L. and Sardanashvily, G. (2002) Connections in classical and quantum field theory. World Science Publishers, Singapore-New York.
- Boulanger, J., le Bihan, N., Catheline, S. and Rosetto, V. (2012) Observation of a non-adiabatic geometric phase for elastic waves. Annals of Physics, 327, 952-958. doi:10.1016/j.aop.2011.11.014
- Žutić, I. and Fabian J. (2007) Spintronics: Silicon twists. Nature, 447, 268-269. doi:10.1038/447269a
- Domcke, W., Yarkony, D. and Koppel, H. (2004) Conical intersections: Electronic structure, dynamics and spectroscopy. World Science, New York.
- El-Nabulsbi, R.A. (2012) Lagrangian and hamiltonian dynamics with imaginary time. Journal of Applied Analysis, 18, 283-295.

