Wireless Engineering and Technology
Vol. 4 No. 2 (2013) , Article ID: 29798 , 10 pages DOI:10.4236/wet.2013.42012
Novel Optimized Cross-Layer Design with Maximum Weighted Capacity Based Resource Allocation for AMC/HARQ Wireless Networks
![]()
1Electronic and Communication Department, Ain Shams University, Cairo, Egypt; 2National Telecommunication Institute, Cairo, Egypt.
Email: reham.elmayet@las.int, heshamelbadawy@ieee.org, sramlye@netscape.net
Copyright © 2013 Reham A. El-Mayet et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 24th, 2012; revised January 6th, 2013; accepted January 19th, 2013
Keywords: AMC; Cross-Layer Design; HARQ; Nakagami-m Fading Channel; QoS
ABSTRACT
To provide quality-of service (QoS) guarantees for heterogeneous applications, most recent wireless communications technologies and standards combine the error-correcting capability of hybrid automatic repeat request (HARQ) schemes at the data link layer (DLL) with the adaptation ability of the adaptive modulation and coding (AMC) modes at the physical layer (PHY) layer. This paper aims to investigate the aggregated system capacity as well as the breakdown of this capacity for different ACM modes in each HARQ scheme. This investigation was done by using maximum weighted capacity (MWC) resource allocation at the PHY layer in conjunction with a novel packet error rate (PER)- based scheduling at the medium access control (MAC) layer. As a result, the dominant AMC mode corresponding to channel SNR was available.
1. Introduction
In order to enhance the throughput of the wireless communication system, link adaptation (LA) technologies are considered not only at the physical layer, but also at the upper-protocol-layers such as data link layer when designing the wireless networks. LA technologies use the instantaneous channel state information (CSI) to adaptively control the data transmission of wireless channel, maintain constant transmission power to reduce the interference of other users and satisfy different business’ needs, and save resources to improve overall throughput for the system. In addition, the adaptive system can easily provide services with different qualities, such as higher information transmission rate, lower packet error rate, and higher spectral efficiency. LA technologies mainly include adaptive modulation and coding (AMC) at the physical layer (PHY) and hybrid automatic repeat request (HARQ) at the data link layer (DLL). The AMC schemes can be used to match transmission rates to timevarying channel, in order to obtain maximum throughput and improve spectral efficiency [1]. Cross-layer design (CLD) which combines AMC and HARQ is extensively studied in order to match the transmission rates to timevarying wireless communication channel conditions [2].
HARQ provides a good tackling technique to solve the tradeoff between channel coding and packet retransmission. It is a well suited solution to enforce the link quality at the medium access control (MAC) layer in wireless environments, and has been adopted in some towards-4G standards (3GPP LTE Release 8, for instance) [3]. It also can be considered as a combination of forward error correction (FEC) and automatic repeat request (ARQ) which is used to improve reliability [1].
A major concern in data communication is how to control transmission errors caused by channel noise so that error-free data can be delivered to the user. A solution to this problem is using HARQ schemes:
Type-I HARQ, the ARQ adopted in 3GPP (R99) is called as HARQ type I. It uses a fixed rate FEC code along with ARQ. In this scheme, both error detection and FEC bits are added to each packet prior to transmission, when the received code word is detected in error, two situations may arise. If the number of errors is within error-correcting capabilities of the code, the errors are corrected. Otherwise, the received coded data block is discarded and a retransmission is requested by the receiver, similar to standard ARQ [4]. The disadvantage of the type I HARQ scheme is that once the code rate is fixed, all parity bits for error correction are transmitted even if they are not all needed, thus reducing the channel use efficiency [5].
Type-II HARQ, it’s an incremental redundancy (IR) HARQ. It considers the time selective property of the wireless channels. At first transmission, the data packet has no or little redundancy. If it fails, each retransmission includes additional redundancy bits from channel encoder; the redundancy is increased in the repeated transmission of the same packet. Thus, retransmission of type-II HARQ only uses the information bits that have not been transmitted in the previous transmissions. If all the channel coded information bits have been transmitted, then the channel code will be retransmitted. When the decoder has received the information packet, it combines all the information packets together to decode. The retransmission packet could not decode alone, it could be decoded only if it was combined together with the previous transmitted information packet [2].
Type-III HARQ, it also an IR scheme but it uses the concept of self-decodable codes; it can be combined with the error data stored and then decoded. The retransmission uses the puncture matrix which is complementary with the puncture matrix for the first transmission. Every puncture matrix has the same code rate and the same error-correction ability [2]. At the receiver, if a frame is detected to be in error, it is stored and a negative acknowledgement (NACK) is fed back. Upon arrival of the retransmission, the receiver attempts to decode the second transmission of the frame. If the decoding is successful, an ACK is fed back; otherwise the frame is stored and combines all the packets together to decode. The retransmission will continue until the decoding is successful or maximum number of transmission has reached [6].
HARQ in 3GPP Long Term Evolution (LTE), both LTE and LTE-Advanced (LTE-A) use HARQ. In LTE, HARQ reordering is done in the radio link control (RLC) layer. So, it operates into different modes: the unacknowledged mode (without ARQ) or in acknowledged mode (with active ARQ). In LTE-A, HARQ is very similar to HARQ in LTE, only small adaptations have been done to cope with the change in the supported bandwidth since LTE-A is supposed to support bandwidth up to 100 MHz [7].
In wireless networking, quality of service (QoS) plays a crucial role in performance measurement. There are four main schemes that are carried out for dynamic subcarrier and power allocation to different OFDM systems users, which allow a flexible multiuser access and enhancement of the multiuser diversity [2]: maximum capacity based resource allocation, proportional fairness based resource allocation, adaptive subcarrier and power allocation in OFDM based on maximizing utility and maximum weighted capacity (MWC) based resource allocation.
The AMC/HARQ CLD concept has been proposed in many literatures such as [1,2,4,6]. In [1], the performance of type I, II, III HARQ with AMC over Nakagami-m fading channel was analyzed, a closed form expression of PER and average spectral efficiency were derived and the conditional probability density function of signal-tonoise ratio (SNR) was calculated using Marcov model. In [2], the HARQ (type-II, type-III) was applied to the cross-layer framework in order to satisfy the prescribed delay and PER constraints at LL. In [4], Jaume Ramis had proposed an analytical link level queuing model to formulate a cross-layer design conceived as a constrained optimization problem to exploit the joint impact on QoS performance of both AMC at the PHY layer and HARQchase combining based-error control at the DLC-layer. Feijn Shi studied the joint design of type-III HARQ protocol at the data link layer and AMC scheme at the PHY layer through closed-form expressions for throughput, average delay and packet loss rate in [6]. Cross-layer scheduling techniques for multiuser OFDM system were introduced in [8,9] by Nan Zhou: in [8], a packet batch based cross-layer scheduling scheme was proposed. This scheme considers the differences between the batches in the same queue, so it is more flexible and efficient than conventional queue based scheduling. In [9], cross-layer resource allocations based on MWC technique and delay satisfaction (DS) scheduling scheme in the downlink multiuser OFDM system were proposed. The current paper will try to investigate the CLD and its enhancements for OFDM based wireless networks. Differently from the previously mentioned publications, the current paper introduces another vision for CLD in both uplink and downlink multiuser OFDM system by considering the packet error rate (PER) as well as the SNR constraints on the overall performance.
In this paper, based on the AMC/HARQ cross-layer design, the system capacity was investigated for different SNR of OFDM channels for different HARQ schemes. Also, a novel PER based data scheduling technique based on MWC resource allocation was proposed.
In Section 2, the system model is presented. Sub-carrier and power allocation are presented in Section 3. PER based data scheduling is presented in Section 4. Numerical results and analysis are shown in Section 5. Finally, Section 6 concludes this paper.
2. System Model
The point-to-point wireless packet communication system under consideration in this paper is illustrated in
Figure 1, showing the most important blocks involved in the transmission and reception processes for a single user. The HARQ protocol with AMC is used over the Nakagami-m fading channel, the channel gain is assumed to be constant during the transmission of one frame, and it varies during the transmission of the next frame. Also, the channel is assumed to support QoS-guaranteed traffic characterized by a packet error rate (PER) and a predetermined acceptable link layer PER Ploss. The processing unit at the data link layer is a packet of fixed size, and the processing unit at the physical layer is a frame made of a variable number of packets that depends on the transmission mode (TM) selected by the AMC scheme. The receiving buffer can accurately detect the received SNR and decide the next modulation scheme, then feedback channel state message to the source node. On the other hand, if the destination node cannot decode the received data packet correctly, it feeds back NACK signaling to the source node, otherwise, it feeds back acknowledge (ACK) signaling, and the transmission of all signaling messages are assumed to be error free, the maximum number of retransmissions is denoted Rmax.
2.1. Channel Modeling
This paper adopts The Nakagami-m channel model. .The probability density function (pdf) of the received SNR γ, is given by [2]:
 (1)
(1)
where, γ is the instantaneous received SNR, and
 is the average received SNR; m is the Nakagami fading parameter (m ≥ 1/2).
is the average received SNR; m is the Nakagami fading parameter (m ≥ 1/2). 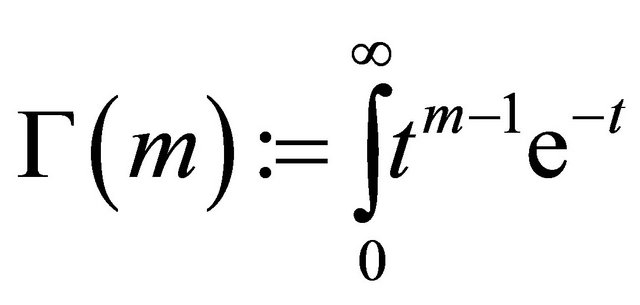 is the gamma function.
is the gamma function.
2.2. Combining AMC with HARQ Schemes
Given γ in the previous channel model, the objective of AMC is to select a suitable TM to maximize the data rate
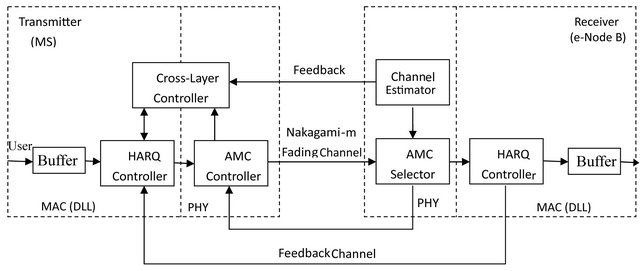
Figure 1. Single link between a single-antenna transmitter (MS) and a single-antenna receiver (e-Node B).
while maintaining a prescribed PER Ploss.
To combine the AMC at PHY and HARQ schemes at LL, only finite delays could be afforded. So, the maximum number of the transmission of one packet Rmax could be determined by dividing the maximum allowable system delay over the round trip delay required for each transmission. If a packet is still erroneous after Rmax transmissions, it will be dropped, packet loss is declared. So, acceptable Ploss should be predetermined [2].
To simplify the design, the following approximate instantaneous PER expression is used [1,2,6]:
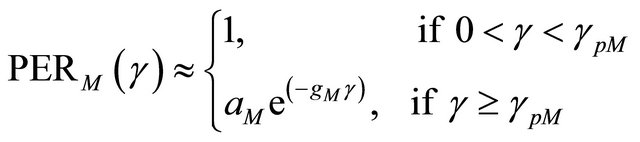 (2)
(2)
here, M is the mode index to identify the AMC mode. The parameters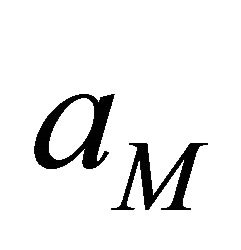 ,
, and
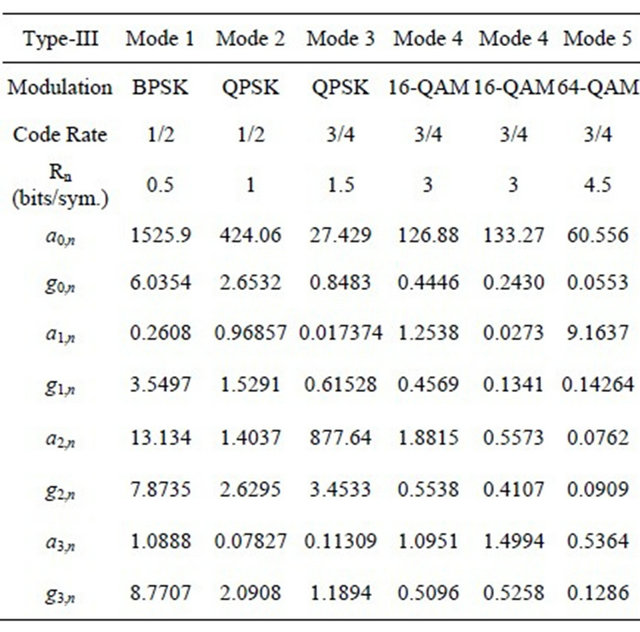
and  are mode-dependent parameters, which are listed in Tables 1 and 2 for packet length Np = 1080 bits. These parameters are obtained by fitting Equation (2) to the exact PER [10]. This expression is used to approximate the PER, when the convolutional code is used. Tables 1 and 2 show the values of these parameters for HARQ-type II and HARQ-type III respectively [2].
are mode-dependent parameters, which are listed in Tables 1 and 2 for packet length Np = 1080 bits. These parameters are obtained by fitting Equation (2) to the exact PER [10]. This expression is used to approximate the PER, when the convolutional code is used. Tables 1 and 2 show the values of these parameters for HARQ-type II and HARQ-type III respectively [2].
In the following Tables 1 and 2, the index r in parameters ar,M and gr,M, represents the number of retransmission. r = 0, 1, 2, 3 represent the first, second, third and fourth transmission. M = 1 - 6 represent the AMC mode.
For the type-I HARQ, PER of each transmission is the same as the first transmission of type-II, III HARQ. So, the parameters a0,M and g0,M are the PER curve fitting parameters of type-I HARQ for each AMC mode. The expression of the PER for type-I HARQ is given by:
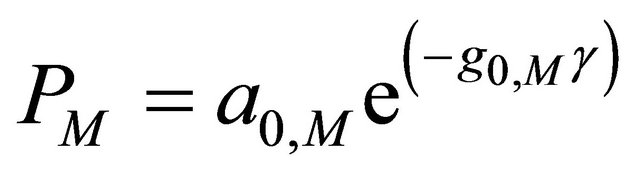 (3)
(3)
Table 1. Transmission modes for type II HARQ [2].

Table 2. Transmission modes for type III HARQ [2].
Based on the parameters in the Tables 1 and 2, the PER curves for the type-II, III HARQ can be calculated from:
 (4)
(4)
P0,M is the PER for the first transmission, 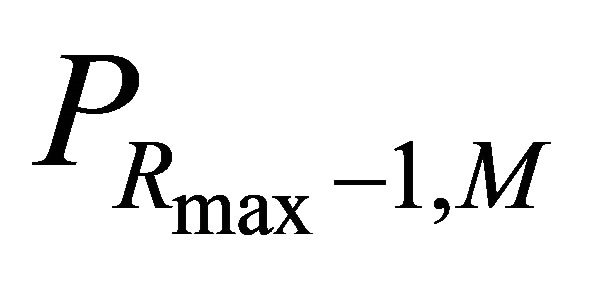
is the PER for the Rmaxth transmission, the index M is the AMC mode.
Equation (5) must be valid, in order to satisfy that the PER is lower than the packet loss probability Ploss after the Rmax transmissions at LL:
 (5)
(5)
Then, the average PER for each mode is given by:
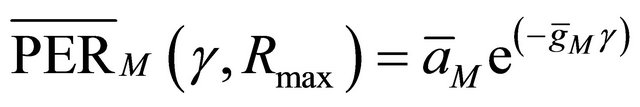 (6)
(6)
where,
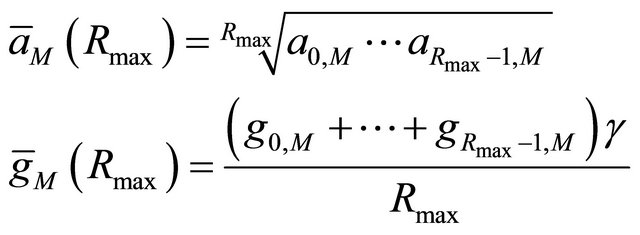 (7)
(7)
For the type-I HARQ, in order to satisfy the PER requirement at LL, 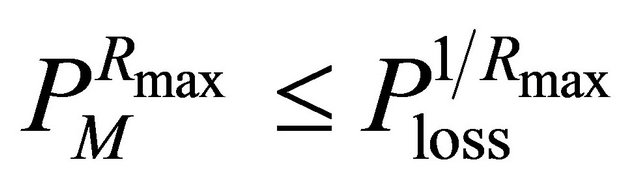 , then we get
, then we get
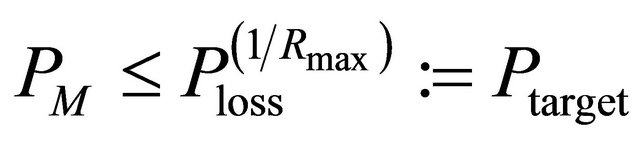 (8)
(8)
2.3. Different AMC Mode Interval Calculation
The parameter Ptarget(Rmax) is a key parameter transferred from LL to PHY. Ptarget(Rmax) transfers the PER constraint Ploss and the time delay requirement Rmax to PHY, in order to control the determination of the intervals for different modulation and coding schemes. The intervals are dynamic because of two reasons: first, Ptarget(Rmax) important factor to determine the intervals and it is affected by Ploss and Rmax; second, PER curve in PHY for each transmission mode  are affected by Rmax. For type-I HARQ, PM is not affected by Rmax. For type-II, and type-III HARQ, PM decreases as Rmax increases. The intervals of different AMC modes can be calculated from the expression [2,6]:
are affected by Rmax. For type-I HARQ, PM is not affected by Rmax. For type-II, and type-III HARQ, PM decreases as Rmax increases. The intervals of different AMC modes can be calculated from the expression [2,6]:
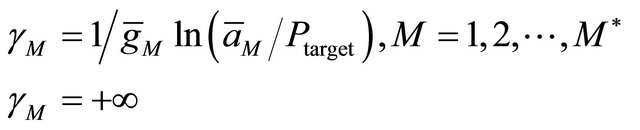 (9)
(9)
By substituting by ,
,  for (type-II & III) and Ptarget into the expression (9), we could figure out the intervals of type-I, II, III HARQ for different transmission modes, when the maximum number of transmission is Rmax and the maximum PER probability is Ploss.
for (type-II & III) and Ptarget into the expression (9), we could figure out the intervals of type-I, II, III HARQ for different transmission modes, when the maximum number of transmission is Rmax and the maximum PER probability is Ploss.
2.4. ACM Model Selection
At PHY layer, when SNR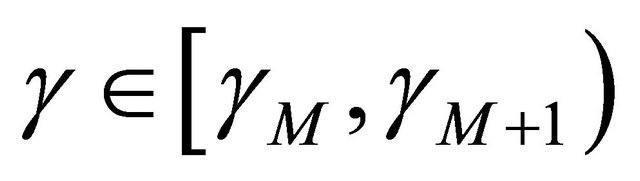 , the mode M modulation and coding will be chosen. So if we put Equation (1) into the expression below, then we will choose mode M with probability [2,6]:
, the mode M modulation and coding will be chosen. So if we put Equation (1) into the expression below, then we will choose mode M with probability [2,6]:
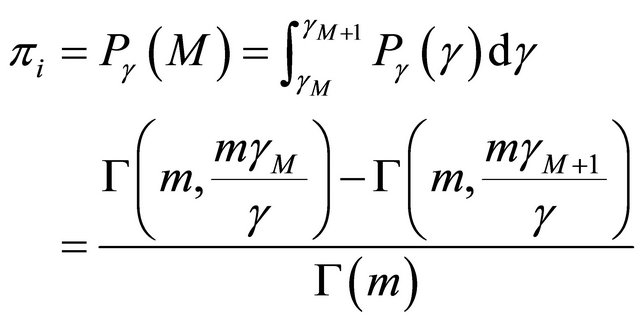 (10)
(10)
where, 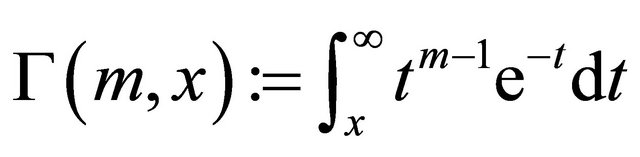 is complementary in complete Gamma function.
is complementary in complete Gamma function.
3. Subcarrier and Power Allocation for the Downlink
By considering a downlink OFDM system with U users, it’s assumed that each subcarrier is occupied by only one user [11]. With cross-layer optimization, the QoS information is transferred from the traffic controller at the MAC layer to the subcarrier, and power controller at the PHY layer for resource allocation. Then, the resource allocation results are fed-back to the traffic controller in the base station for scheduling of the data to be sent out in each slot [8].
In consistence with [9], this paper assumes a total bandwidth of B shared by N subcarriers, and the OFDM signaling is time slotted. Each slot has duration of Tslot. Let, Ωu denotes the index set of subcarriers allocated to user u . Let pu,n be the power allocated to user u on subcarrier n; (n ∊ Ωu). hu,n is the corresponding channel gain. No is the power spectral density of Additive White Gaussian Noise (AWGN). By assuming perfect channel estimation, the achievable data rate of user u on subcarrier n is expressed as [9]:
. Let pu,n be the power allocated to user u on subcarrier n; (n ∊ Ωu). hu,n is the corresponding channel gain. No is the power spectral density of Additive White Gaussian Noise (AWGN). By assuming perfect channel estimation, the achievable data rate of user u on subcarrier n is expressed as [9]:
 (11)
(11)
where,
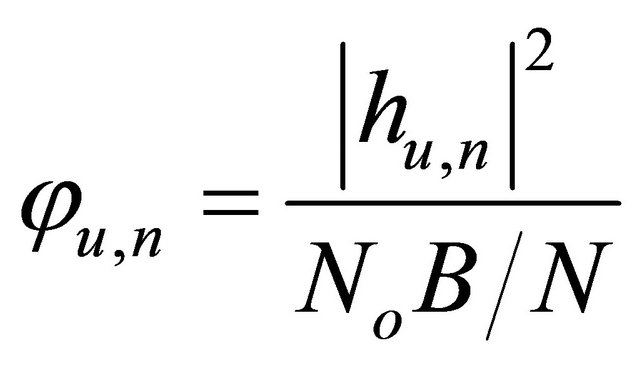 (12)
(12)
is the channel-to-noise power ratio for user u on subcarrier n.
Therefore, the total data rate of user u is given by:
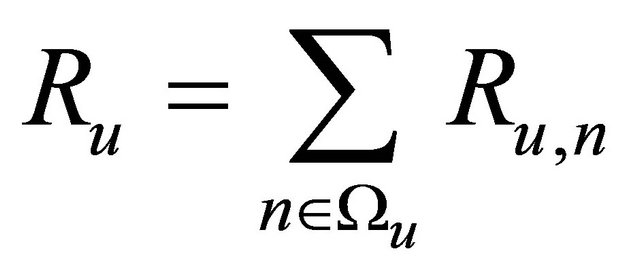 (13)
(13)
A resource allocation scheme had been proposed in [2], to maximize the weighted sum of all users’ capacity J, i.e., to maximize
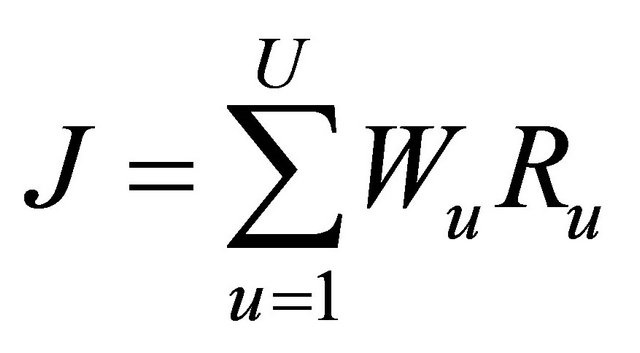 (14)
(14)
Subject to: 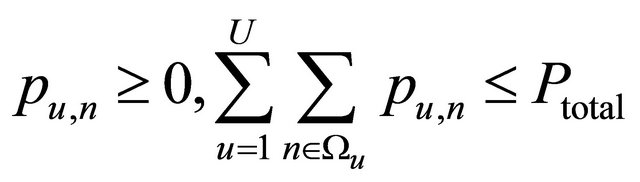
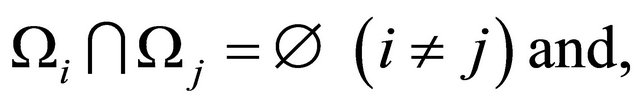
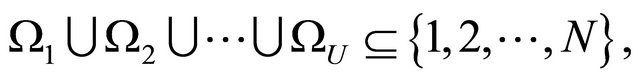
where, Wu denotes the weight for user u, which is evaluated based on the cross-layer optimization criteria. So it indicates the QoS information for user u, and is obtained from the result of data scheduling at the MAC layer as will be investigated in Section 4 and Ptotal denotes the total power.
The optimization process is divided into two stages namely, subcarrier allocation and power allocation.
3.1. Optimal MWC Based Subcarrier Allocation
For simplicity, by assuming uniform power allocation across all subcarriers, i.e., each subcarrier is allocated a power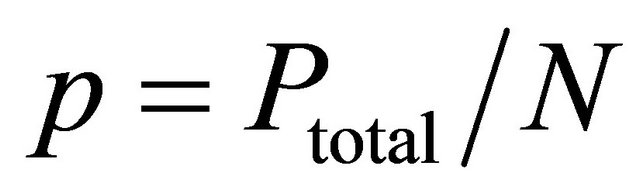 . Optimal subcarrier allocation leads to the maximum cost function, which is denoted by Jmax. If an arbitrary subcarrier n allocated to user u
. Optimal subcarrier allocation leads to the maximum cost function, which is denoted by Jmax. If an arbitrary subcarrier n allocated to user u 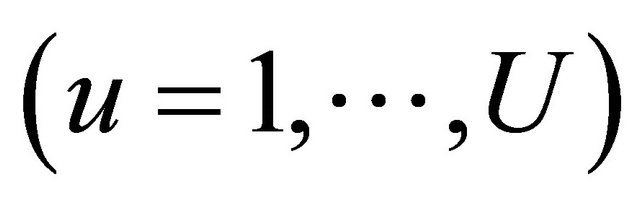 with optimal subcarrier allocation is now reassigned to user s, let
with optimal subcarrier allocation is now reassigned to user s, let 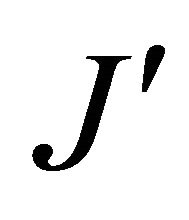 denote the resulting cost function. The difference between the two cost functions is given by [9]:
denote the resulting cost function. The difference between the two cost functions is given by [9]:
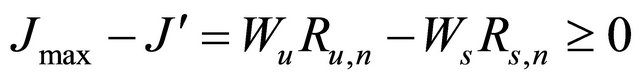 (15)
(15)
Substituting (11) into (15), we have
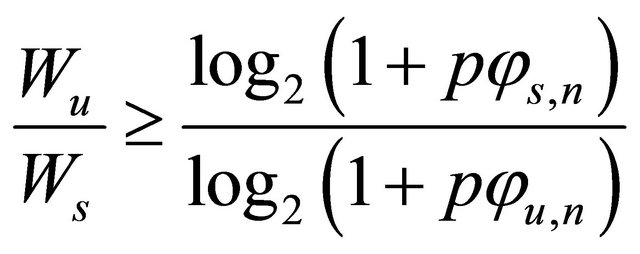 (16)
(16)
which implies that, with optimal subcarrier allocation, subcarrier n should be allocated to user u rather than users if Equation (16) is satisfied. However, it is prohibitively complex to perform optimal subcarrier allocation with a large number of subcarriers. Therefore, a suboptimal scheme is desired.
• Suboptimal MWC based subcarrier allocation Intuitively, to maximize the cost function in Equation (14), a larger weight demands a higher data rate. Let Ru/Wu denote the Rate-to-Weight Ratio (RWR) and assuming uniform power allocation across all subcarriers. Then, the following suboptimal subcarrier allocation scheme is employed, where the user with the lowest RWR is allowed to pick subcarriers in each of iteration [9]:
1) Initialization:
a) Set Ru =0,  for all u
for all u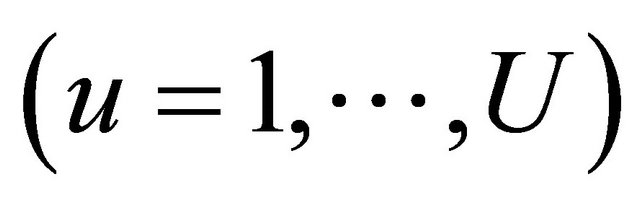 , sort Wu in the descending order, and let
, sort Wu in the descending order, and let 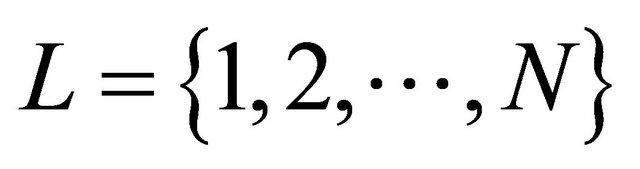 denote the set of unallocated subcarriers.
denote the set of unallocated subcarriers.
For u = 1 to U:
b) If 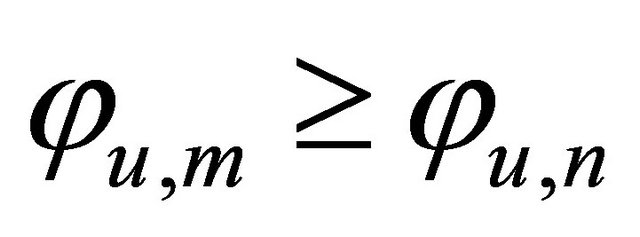 (
(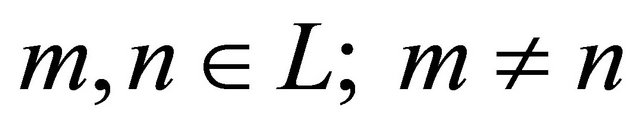 ), assign subcarrier m to user u, i.e., add subcarrier m to Ωu. Remove subcarrier m from L. Update Ru according to Equation (5).
), assign subcarrier m to user u, i.e., add subcarrier m to Ωu. Remove subcarrier m from L. Update Ru according to Equation (5).
2) Find the minimum Ru/Wu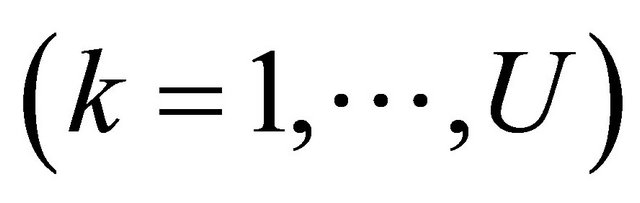 , and repeat 1 b) for the corresponding user u.
, and repeat 1 b) for the corresponding user u.
3) Repeat 2) until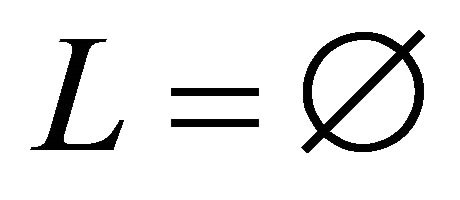 .
.
3.2. Optimal MWC Based Power Allocation
Following subcarrier allocation, the optimal power allocation for each user can be obtained by using the Lagrange multiplier, i.e., (14) can be rewritten as:
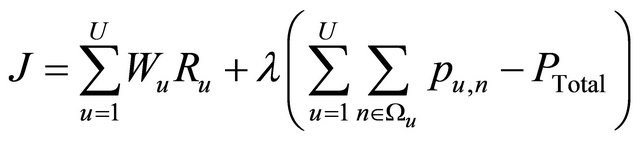 (17)
(17)
Subject to 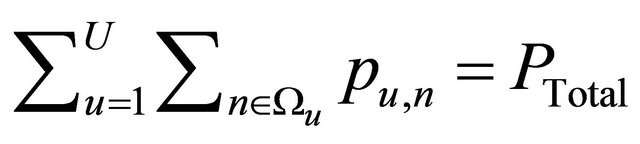 and pu,n ≥ 0. Letting
and pu,n ≥ 0. Letting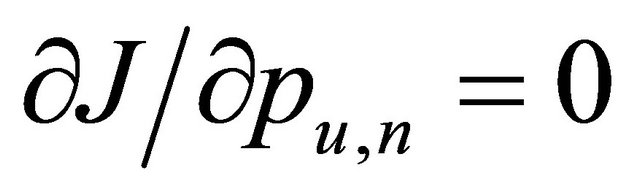 , the optimal solution for pu,n is given by:
, the optimal solution for pu,n is given by:
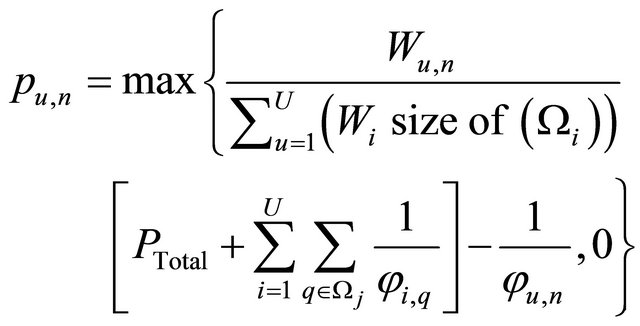 (18)
(18)
Consider users j and u (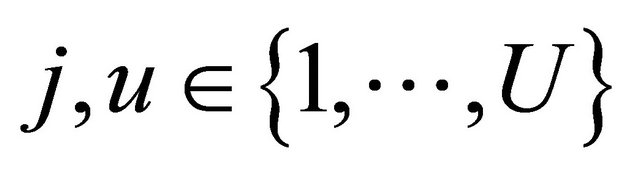 ), and subcarrier m ∊ Ωj and n ∊ Ωu are two arbitrary subcarriers allocated to users j and u, respectively. By
), and subcarrier m ∊ Ωj and n ∊ Ωu are two arbitrary subcarriers allocated to users j and u, respectively. By , we can drive:
, we can drive:
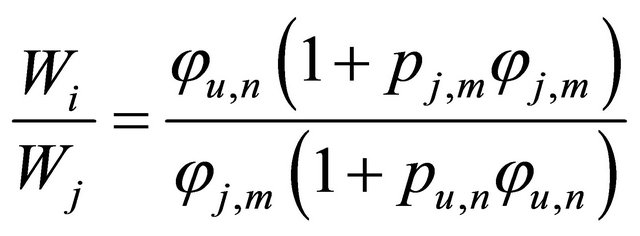 (19)
(19)
1) If Wj/Wu = 1, from (19) it can be derived that:
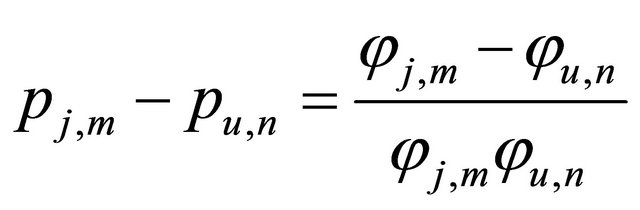 (20)
(20)
Equation (20) implies that with equal weight, the subcarrier with a better channel gain is allocated more power, which is the same result as water-filling [12].
2) If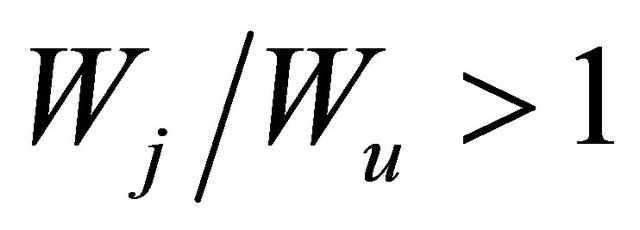 , we have:
, we have:
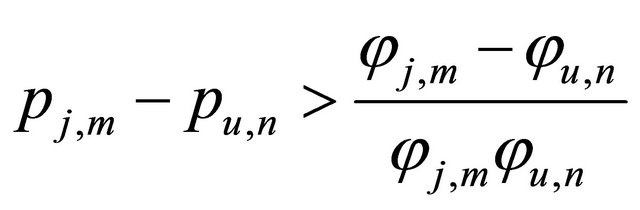 (21)
(21)
Equation (21) implies that the subcarrier corresponding to the user with a higher weight is allocated more power than the case using water-filling.
4. Packet Error Rate Based Data Scheduling
After receiving the resource allocation results from the PHY layer, which indicates the amount of data allowed for each user, the MAC layer performs scheduling for each batch of data to be sent out. This paper proposes a novel scheduling scheme, which assigns the weight depending on the average PER in each ACM mode, after the intervals of different ACM modes are calculated from Equation (9).
The weight Wu denotes the weight of the batch of user u corresponding to the ACM mode Mi, which is given by:
 (22)
(22)
where, Ti is the total number of users in ACM mode i, and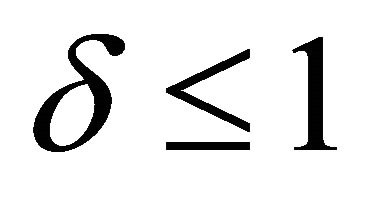 .
.
Equation (22) gives higher priority to the user whose batch of data has the maximum PER.
To give the higher priority to the user whose batch of data has the minimum PER, the following equation may be used:
 (23)
(23)
5. Numerical Results and Analysis
In order to investigate the proposed cross-layer optimization scheme, numerical results will be deduced for HARQ schemes over a Nakagami-m fading channel. The data unit is assumed to be one frame, and each frame contains a fixed number of symbols. The receiving buffer can accurately detect the received γ and decides the next modulation scheme, then feedback channel state message to the source node; on the other hand, if the destination node cannot decode the received data packet correctly, it feeds back NACK signaling.
5.1. SNR Margins for Different HARQ Modes
In order that, the different modulation and coding schemes is assessed in the case of having only the AWGN. So, Figure 2 presents the obtained probability of PER against the apparent SNR for different AMC modes.
Figures 2 and 3 show the case of having different SNR margins to sustain the PER at a certain range. The obtained results in Figures 2 and 3 are in consistence with those published in many references as [1,2].
The retransmission technique depends on the used HARQ scheme. Also, it is assumed that the transmissions of all signaling messages are assumed to be error free, maximum number of retransmissions, Rmax = 4 and the ACM modes M = 6.

Figure 2. Different ACM modes for type II HARQ.
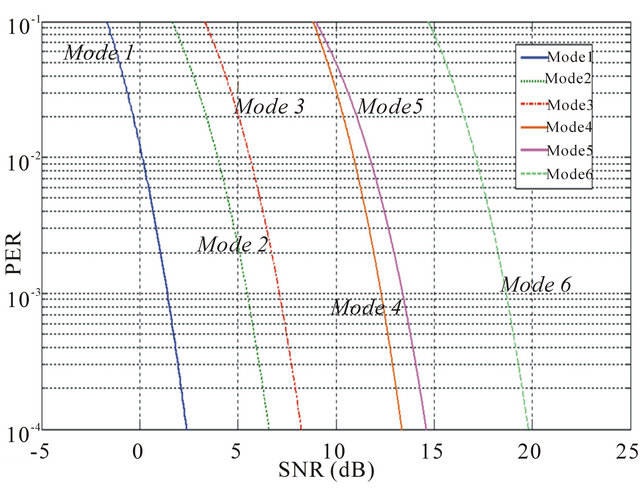
Figure 3. Different ACM modes for type III HARQ.
5.2. Effect of Proposed PER Scheduling Criteria on the System Capacity
This paper employs the proposed MWC based resource allocation at the PHY layer and the PER based scheduling at the MAC layer for consistency. It considers a LTE system listed in [13], with U = 100 users, a total transmit power of Ptotal = 1 W, a total bandwidth of B = 10 MHz, subcarrier width of 15 KHz, physical source block code of 180 KHz bandwidth and 50 available Physical Resource Block (PRB). The power spectral density of AWGN is N0 = −80 dBW/Hz [9] and δ in Equations (22) and (23) is taken to be 0.8.
Figures 4 and 5 show the obtained throughput for each mode by deploying the minimum PER using Equation (23) after running different number of iterations with different HARQ techniques. Whereas, Figures 6 and 7 show the obtained throughput for each mode by deploying the maximum PER using Equation (22) after running different number of iterations with different HARQ techniques.
So, it may be noticed that, the PER maximum as well as the minimum margins are closely estimating the vali-

Figure 4. Average SNR against system capacity (J) HARQ type II-minimum PER.
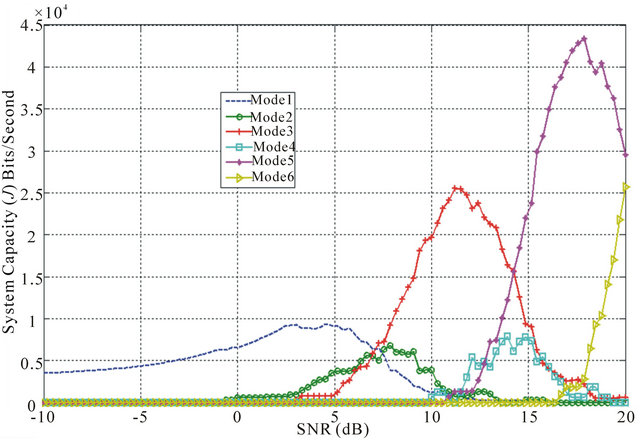
Figure 5. Average SNR against system capacity (J) HARQ type III-minimum PER.
dation range for each AMC mode separately. This may be explained as a result of having good and stable CLD optimization for different AMC modes with different HARQ.
5.3. Effect of Service Requests on HARQ-Type III
Figures 8-10, are investigating the effect of having more customers talking on the same Enhanced e-NodeB site and contenting upon the available throughput.
So, these figures show that by increasing the number of customers, it’s noticed that there’s a steady increase in the required SNR to achieve the same throughput. This may be explained by that the system will be more starving to the power in order to overwhelm the existing interference which arises from the existing customers.
5.4. LTE System Capacity with Proposed CLD Based PER Scheduling
In Figures 11-14, it is shown that for LTE system parameters, HARQ type III will have much better performance (aggregated throughput) than that of HARQ type II. This
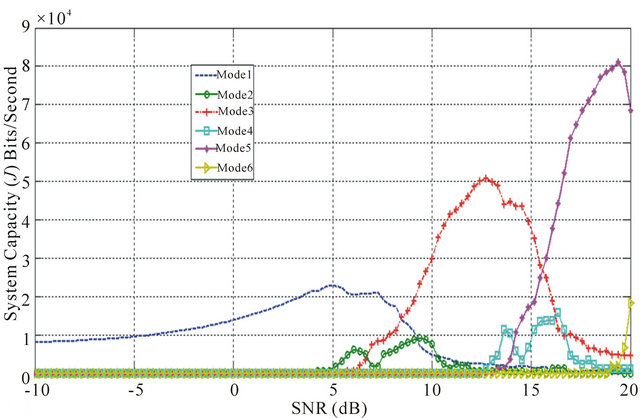
Figure 6. Average SNR against system capacity (J) HARQ type II-maximum PER.

Figure 7. Average SNR against system capacity (J) HARQ type III-maximum PE.
may be explained by that the HARQ type III will have higher coding gain so, the obtained throughput is improved and can be achieved in lower SNR (compared to HARQ type II required SNR).
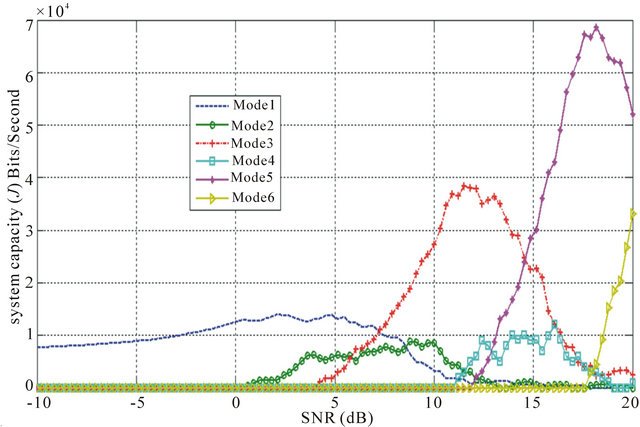
Figure 8. Average SNR against system capacity (J) K = 100- HARQ type III.
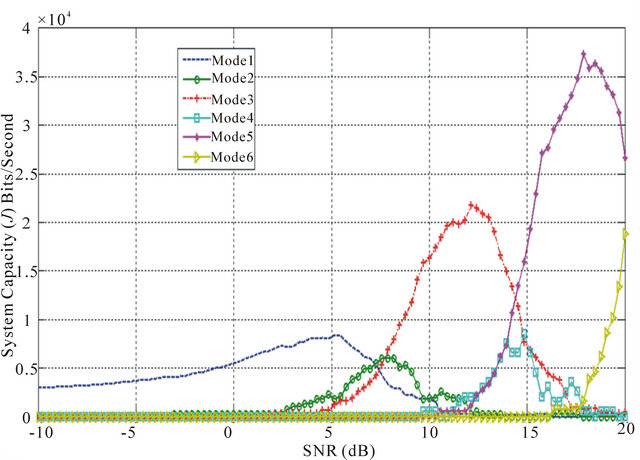
Figure 9. Average SNR against system capacity (J) K = 200- HARQ type III.

Figure 10. Average SNR against system capacity (J) K = 300-HARQ type III.
 (a)
(a)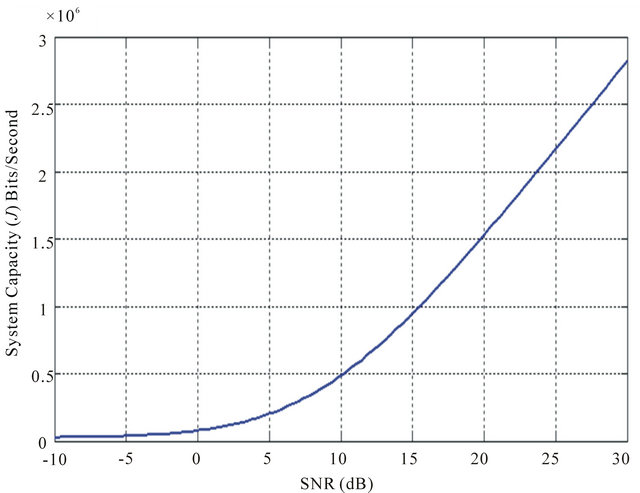 (b)
(b)
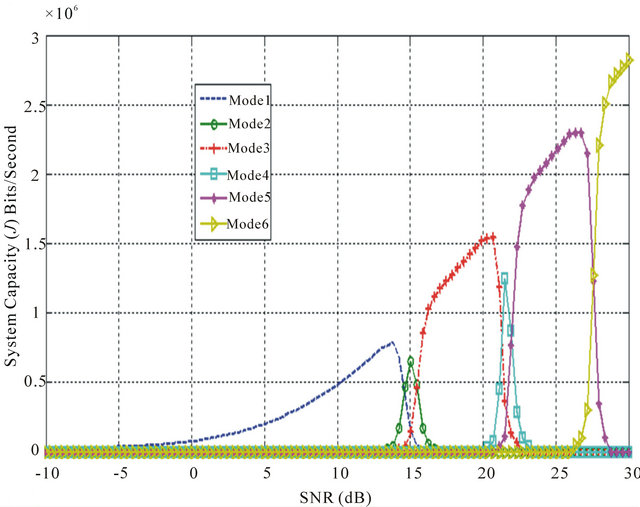
Figure 11. (a) Average SNR against system capacity (J) for each mode in LTE system with proposed maximum PER based scheduling-HARQ type II; (b) Average SNR against aggregated system capacity (J) in LTE system with proposed maximum PER based scheduling-HARQ type II.
6. Conclusion
A novel optimized cross-layer design (CLD) for AMC/ HARQ wireless networks was presented. In this paper, MWC resource allocation at PHY layer is used. In addition, the new PER based data scheduling is proposed in order to investigate the aggregated throughput, after developing AMC/HARQ schemes. Also, this paper introduces an analysis and complete investigation for breaking down of different AMC modes in the same HARQ scheme. The concurrent paper aims to put in the spot the relation between the dominant operational ACM modes in conjunction with the available SNR, which will be useful for practical implementation and deployment for the cross-layer design of certain operator or service provider.
 (a)
(a)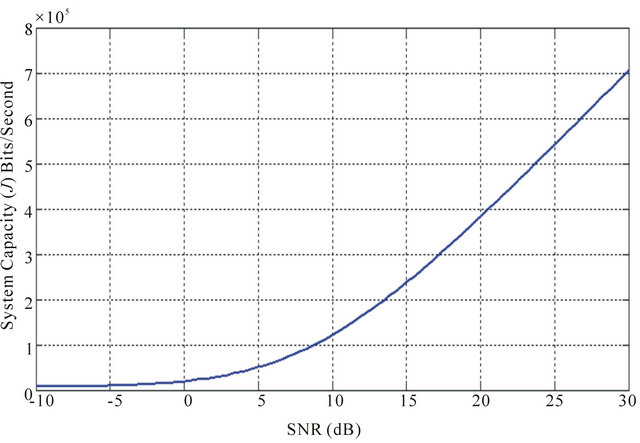 (b)
(b)
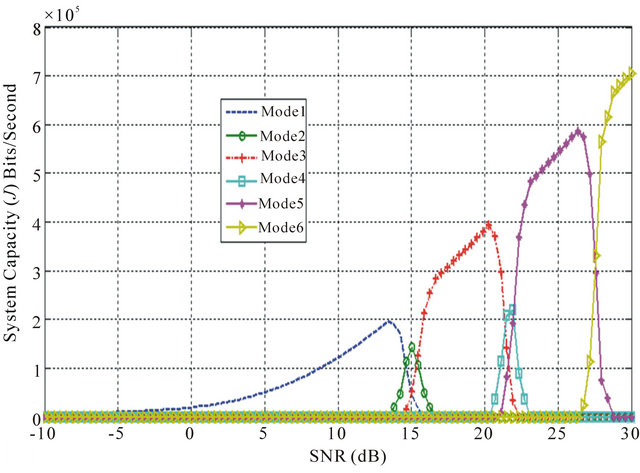
Figure 12. (a) Average SNR against system capacity (J) for each mode in LTE system with proposed minimum PER based scheduling-HARQ type II; (b) Average SNR against aggregated system capacity (J) in LTE system with proposed minimum PER based scheduling-HARQ type II.
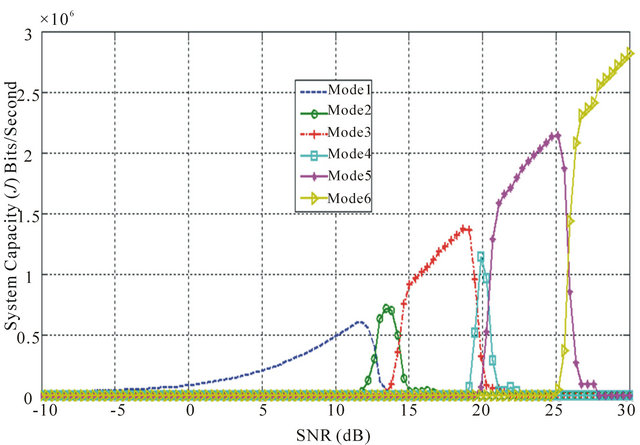 (a)
(a) (b)
(b)
Figure 13. (a) Average SNR against system capacity (J) for each mode in LTE system with proposed maximum PER based scheduling-HARQ type III; (b) Average SNR against aggregated system capacity (J) for each mode in LTE system with proposed maximum PER based scheduling-HARQ type III.
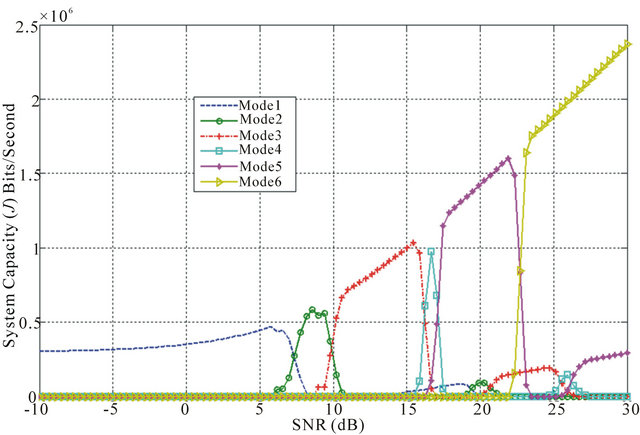 (a)
(a)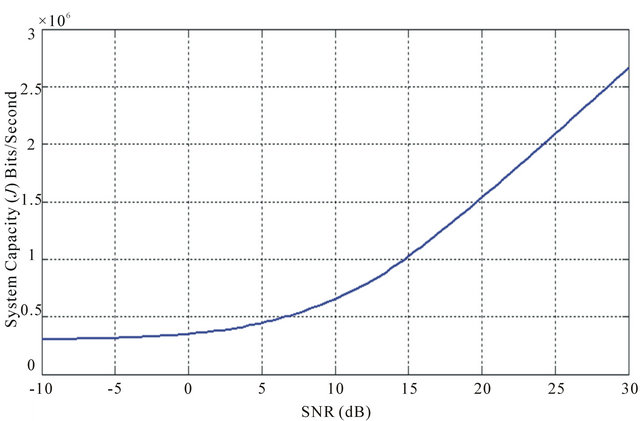 (b)
(b)
Figure 14. (a) Average SNR against system capacity (J) for each mode in LTE system with proposed minimum PER based scheduling-HARQ type III; (b) Average SNR against aggregated system capacity in LTE system with proposed minimum PER based scheduling-HARQ type III.
REFERENCES
- C.-Q. Dai, Y. Rao, L. Jiang, Q.-B. Chen and Q. Huang, “Cross-Layer Design of Combining HARQ with Adaptive Modulation and Coding for Nakagami-m Fading Channels,” Journal of Communications, Academy Publisher, Vol. 7, No. 6, 2012, pp. 458-463.
- C. C. Li, L. L. Xu and D. F. Yuan, “Performance Analysis and Comparison of HARQ Schemes in Cross Layer Design,” Fourth International Conference on Communications and Networking in China, Ji’nan, 26-28 August 2009, pp. 1-5.
- S. Marcille, P. Ciblat and C. J. Le Martret, “A CrossLayer HARQ scheme Robust to Imperfect Feedback,” 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers, 4-7 November 2012, pp. 143-147.
- J. Ramis, G. Femenias, F. Riera-Palou and L. Carrasco, “Cross-Layer Optimization of Adaptive Multi-Rate Wireless Networks Using Truncated Chase Combining HARQ,” Global Telecommunications Conference, Palma de Mallorca, 6-10 December 2010, pp. 1-6.
- S. Kallel and D. Haccoun, “Generalized Type II Hybrid ARQ Scheme Using Punctured Convolutional Coding,” IEEE Transactions on Communications, Vol. 38, No. 11, 1990, pp. 1938-1946. doi:10.1109/26.61474
- F. Shi, D. Yuan and L. Xu, “Performance Analysis of Type-III HARQ Scheme in Cross-Layer Design for QuosGuaranteed Traffic,” International Workshop on Cross Layer Design, Ji’nan, 20-21 September 2007, pp. 133-137. doi:10.1109/IWCLD.2007.4379055
- A. M. Cipriano, P. Gagneuri, G. Vivier and S. Sezginer, “Overview of ARQ and HARQ in Beyond 3G System,” IEEE 21st International Symposium on Personal, Indoor and Mobile Radio Communications Workshops, Colombes, 26-30 September 2010, pp. 424-429.
- N. Zhou, X. Zhu, Y. Huang and H. Lin, “Novel Batch Dependant Cross-Layer Scheduling for Multiuser OFDM Systems,” IEEE International Conference, Beijing, 19-23 May 2008, pp. 3878-3882.
- N. Zhou, X. Zhu and Y. Huang, “Cross-Layer Optimization with Guaranteed QoS for Wireless Multiuser OFDM Systems,” IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, 3-7 September 2007, pp. 1-5.
- X. Wang, Q. Liu and G. B. Giannakis, “Analyzing and Optimizing Adaptive Modulation Coding Jointly with ARQ for QoS-Guaranteed Traffic,” IEEE Transactions on Vehicular Technology, Vol. 56, No. 2, 2007, pp. 710- 720. doi:10.1109/TVT.2007.891465
- Z. Shen, J. G. Andrews and B. L. Evans, “Adaptive Resource Allocation in Multiuser OFDM Systems with Proportional Rate Constraints,” IEEE Transactions on Wireless Communications, Vol. 4, No. 6, 2005, pp. 2726-2737. doi:10.1109/TWC.2005.858010
- T. M. Cover and J. A. Thomas, “Elements of Information Theory,” Wiley, New York, 1991. doi:10.1002/0471200611
- “3GPP Long Term Evolution: System Overview, Product Development and Test Challenges,” Agilent Technology, 2009. http://cp.literature.agilent.com/litweb/pdf/5989-8139EN.pdf

