Wireless Engineering and Technology
Vol.3 No.1(2012), Article ID:16942,7 pages DOI:10.4236/wet.2012.31003
Improving Bandwidth of Yagi-Uda Arrays
![]()
Cataldo & Fisher, LLC, Woburn, USA.
Email: rf2@ieee.org
Received October 13th, 2011; revised October 30th, 2011; accepted November 18th, 2011
Keywords: Variable Z0; Z0; Characteristic Impedance; Feed System; Antenna; Antenna Design; Antenna Optimization; Design Objectives; Performance Objectives; Bandwidth; Impedance Bandwidth; Broadband; Ultra Wideband; UWB; Yagi; Yagi-Uda; Central Force Optimization; CFO; Numerical Optimization; Optimization Algorithm; Metaheuristic; Dominating Cone Line Search; DCLS
ABSTRACT
A novel approach for improving antenna bandwidth is described using a 6-element Yagi-Uda array as an example. The new approach applies Central Force Optimization, a deterministic metaheuristic, and Variable  technology, a novel, proprietary design and optimization methodology, to produce an array with 33.09% fractional impedance bandwidth. This array’s performance is compared to its CFO-optimized Fixed
technology, a novel, proprietary design and optimization methodology, to produce an array with 33.09% fractional impedance bandwidth. This array’s performance is compared to its CFO-optimized Fixed 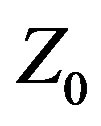 counterpart, and to the performance of a 6-element Dominating Cone Line Search-optimized array. Both CFO-optimized antennas exhibit better performance than the DCLS array, especially with respect to impedance bandwidth. Although the Yagi-Uda antenna was chosen to illustrate this new approach to antenna design and optimization, the methodology is entirely general and can be applied to any antenna against any set of performance objectives.
counterpart, and to the performance of a 6-element Dominating Cone Line Search-optimized array. Both CFO-optimized antennas exhibit better performance than the DCLS array, especially with respect to impedance bandwidth. Although the Yagi-Uda antenna was chosen to illustrate this new approach to antenna design and optimization, the methodology is entirely general and can be applied to any antenna against any set of performance objectives.
1. Introduction
This note describes a novel approach to improving antenna bandwidth using a six-element Yagi-Uda array as an example. Developed more than 85 years ago [1,2], the “Yagi” still is widely used, but it is inherently narrowband, to quote: “Usually Yagi-Uda arrays have low input impedance and relatively narrow bandwidth (on the order of about 2%)” [3, p.396]. Modern well-designed Yagis achieve greater bandwidth, on the order of 5% [4] to more than 15% [5], but these bandwidths still are far below the requirements of many wireless systems. The Federal Communications Commission, for example, defines an Ultra Wideband (UWB) antenna as having a fractional impedance bandwidth (IBW) of at least 20%, or an absolute bandwidth of 500 MHz [6, p.15]. Central Force Optimization (CFO) and Variable 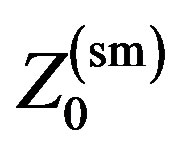 1 technology (Var
1 technology (Var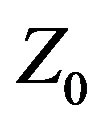 ,
,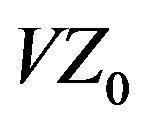 ) are applied to the Yagi design problem, and the array’s IBW performance is compared to another state-of-the-art design. The CFO-
) are applied to the Yagi design problem, and the array’s IBW performance is compared to another state-of-the-art design. The CFO- Yagi achieves a very robust IBW of 33.09% for VSWR ≤ 2:1.
Yagi achieves a very robust IBW of 33.09% for VSWR ≤ 2:1.
2. Yagi-Uda Array
The 6-element array comprises a center-fed driven element (DE) excited by a radio-frequency (RF) source flanked by a parasitic reflector (REF) on one side and four parasitic directors ( ,
, ) on the other. All elements are PEC (Perfectly Electrically Conducting). Three Yagis are described in this paper. Two were optimized with CFO, one using Variable
) on the other. All elements are PEC (Perfectly Electrically Conducting). Three Yagis are described in this paper. Two were optimized with CFO, one using Variable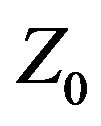 , which treats
, which treats 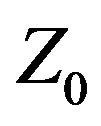 as an unknown variable whose value is to be determined by the optimization algorithm [7,8], and the other using the traditional approach of assigning
as an unknown variable whose value is to be determined by the optimization algorithm [7,8], and the other using the traditional approach of assigning  a fixed value (50 Ω resistive in this case). These two antennas are referred to, respectively, as CFO-VZ0 and CFO-FZ0. CFO was selected as the optimization algorithm because it has performed well against recognized benchmark functions and problems in applied electromagnetics [9-18] and is a useful tool for antenna optimization.
a fixed value (50 Ω resistive in this case). These two antennas are referred to, respectively, as CFO-VZ0 and CFO-FZ0. CFO was selected as the optimization algorithm because it has performed well against recognized benchmark functions and problems in applied electromagnetics [9-18] and is a useful tool for antenna optimization.
The third antenna was optimized with Dominating Cone Line Search (DCLS) [5] and therefore provides a state-of-the-art comparison. The “A3” Yagi, whose dimensions are adapted from in table IV in [5] (REF moved to the Y-axis), was chosen for comparison because it has the largest bandwidth of the three antennas discussed in that paper. Both CFO and DCLS are deterministic algorithms, thus providing the major advantage compared to stochastic algorithms of returning the same results for every run with the same setup.
The Yagis’ performance was computed using NEC- 4.2D (Numerical Electromagnetics Code ver. 4.2 double precision) [19-21]. NEC is a widely used Method of Moments (MoM) wire structure modeling program developed at Lawrence Livermore National Laboratory (LLNL). A freeware version of NEC-2 is available online (source code, executables and a GUI) [22,23]. The modeled antennas are shown in Figure 1 (visualized using 4nec2 [22], the red circle indicating the RF source with the axis length being 1 meter for scaling). Each design’s geometry is quite different.
Table 1 shows element lengths and positions along the boom (+X-axis). Dimensions are in wavelengths, 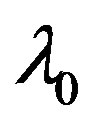 , at the design frequency,
, at the design frequency,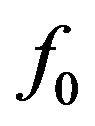 . The corresponding NEC input files appear in Figure 2. Because NEC requires dimen-
. The corresponding NEC input files appear in Figure 2. Because NEC requires dimen-
 CFO-VZ0
CFO-VZ0 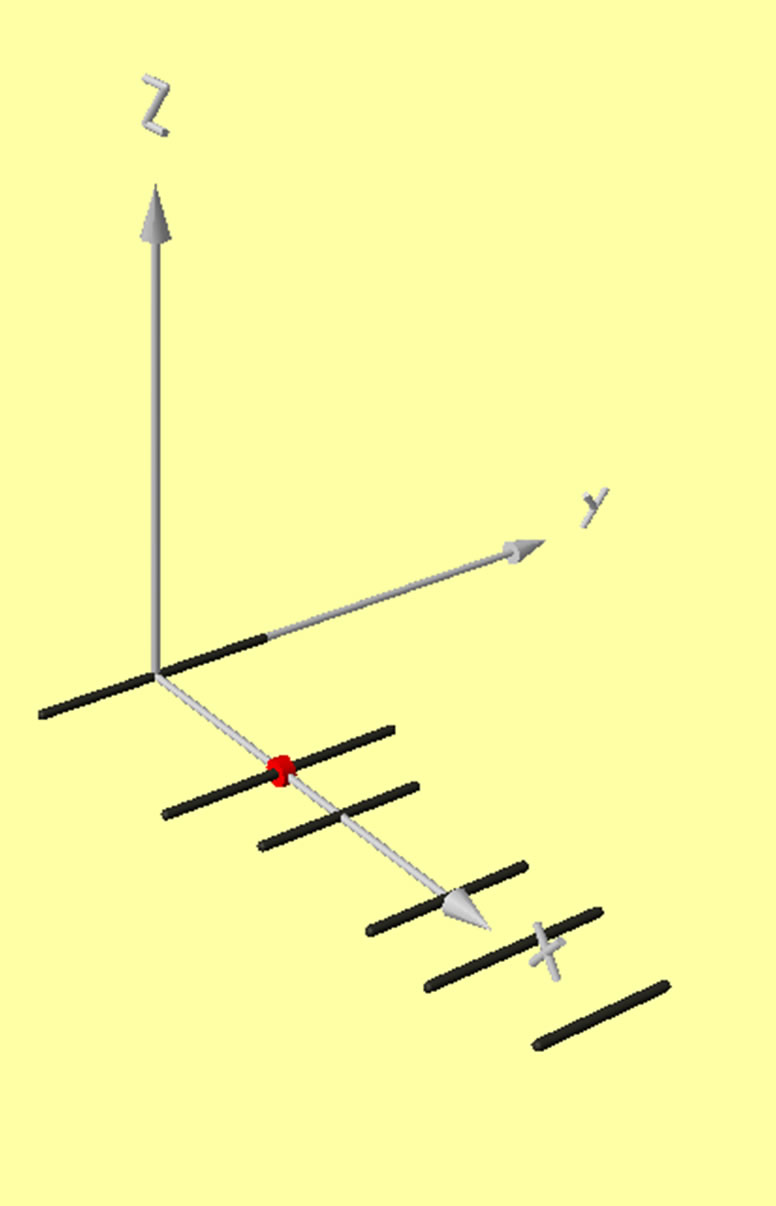 CFO-FZ0
CFO-FZ0 
A3 Figure 1. 6-element yagis.

Table 1. Yagi element lengths & boom positions.
sions in meters, 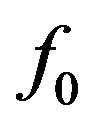 was chosen to be 299.8 MHz corresponding to a wavelength of
was chosen to be 299.8 MHz corresponding to a wavelength of  meter. The Yagi designs therefore can be scaled to any frequency because dimensions in meters are in wavelengths at
meter. The Yagi designs therefore can be scaled to any frequency because dimensions in meters are in wavelengths at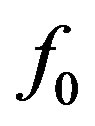 . The element radius was set to 0.009097 meter (or
. The element radius was set to 0.009097 meter (or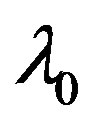 ) because that value is used in [5]. Note that the design frequency
) because that value is used in [5]. Note that the design frequency 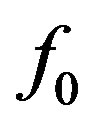 and the band center frequency,
and the band center frequency,  , discussed below are not (necessarily) the same. Even though the array is designed at a particular frequency, the optimized design’s best performance may be (likely is) in a band whose center frequency is different.
, discussed below are not (necessarily) the same. Even though the array is designed at a particular frequency, the optimized design’s best performance may be (likely is) in a band whose center frequency is different.
3. CFO-Variable Z0
The objective function (fitness) to be maximized by CFO was defined as
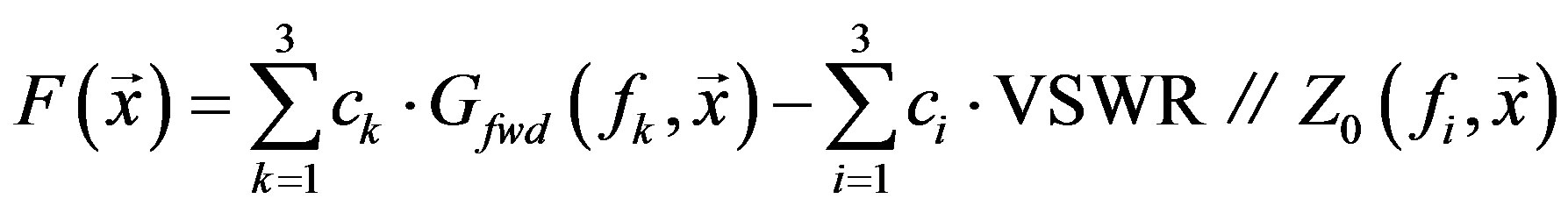
where  is the frequency and
is the frequency and 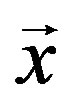 the decision vector defined as
the decision vector defined as
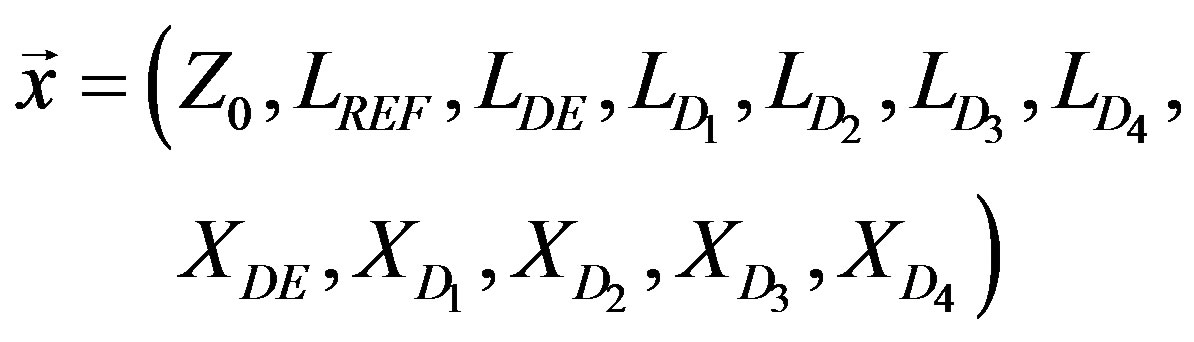
The Yagi optimization problem is 12-dimensional with the following decision variables: , the feed system characteristic impedance (or source internal impedance if there is no feed line); and the eleven geometric variables corresponding to the Yagi element lengths (“
, the feed system characteristic impedance (or source internal impedance if there is no feed line); and the eleven geometric variables corresponding to the Yagi element lengths (“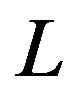 ”) and boom coordinates (“
”) and boom coordinates (“ ”), each subscripted with the corresponding element name (note that REF is placed symmetrically on the Y-axis, that is, at
”), each subscripted with the corresponding element name (note that REF is placed symmetrically on the Y-axis, that is, at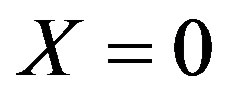 ). The fitness increases with increasing forward gain
). The fitness increases with increasing forward gain  and decreasing
and decreasing ,
, 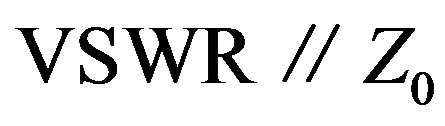 being the voltage standing wave ratio relative to
being the voltage standing wave ratio relative to  (// denotes “relative to”). The fitness is evaluated at three frequencies as shown in Table 2 using the empirically determined coefficients
(// denotes “relative to”). The fitness is evaluated at three frequencies as shown in Table 2 using the empirically determined coefficients  and
and .
.  is evaluated in the direction of the + X-axis (θ = 90˚, φ = 0˚ in NEC’s right-handed spherical polar coordinate system). Algorithm details and a complete source code listing are available online [8], and an electronic listing is available upon request to the author (rf2@ieee.org).
is evaluated in the direction of the + X-axis (θ = 90˚, φ = 0˚ in NEC’s right-handed spherical polar coordinate system). Algorithm details and a complete source code listing are available online [8], and an electronic listing is available upon request to the author (rf2@ieee.org).
The objective function is designed to maximize gain and bandwidth. The term “bandwidth” refers generally to the range of frequencies over which some specific an-

Table 2. Fitness coefficients.
Figure 2. (a) CFO-VZ0; (b) CFO-FZ0; (c) A3.
tenna performance measure is met. For example, “gain bandwidth” is the frequency range over which a minimum power gain is achieved, and so on with respect to other performance measures. IBW is defined as the frequency band or bands within which the antenna input impedance, 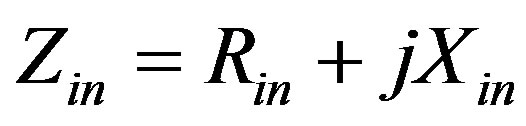 ,
, 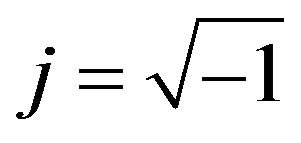 , is matched to the feed system characteristic impedance,
, is matched to the feed system characteristic impedance,  , within specified limits. The desired degree of matching can be specified in many ways, for example, in terms of the antenna’s actual input impedance (resistance,
, within specified limits. The desired degree of matching can be specified in many ways, for example, in terms of the antenna’s actual input impedance (resistance,  , and reactance,
, and reactance, ) as a function of frequency, or, as is more often the case in practice, in terms of a maximum VSWR. IBW typically is specified as
) as a function of frequency, or, as is more often the case in practice, in terms of a maximum VSWR. IBW typically is specified as 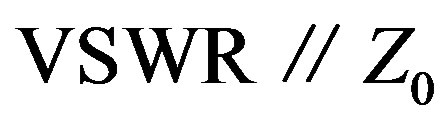 ≤ 2:1, which is equivalent to a return loss (scattering parameter
≤ 2:1, which is equivalent to a return loss (scattering parameter ) approximately less than –10 dB. Other VSWR thresholds can be used instead, and frequently are. Military systems, for example, often use a 3:1 threshold. Zehforoosh et al. [24] describe the design of an UWB microstrip antenna and provide a good summary of
) approximately less than –10 dB. Other VSWR thresholds can be used instead, and frequently are. Military systems, for example, often use a 3:1 threshold. Zehforoosh et al. [24] describe the design of an UWB microstrip antenna and provide a good summary of ’s significance as a design parameter in the context of IBW.
’s significance as a design parameter in the context of IBW.
Of course, the antenna designer is free to specify any desired fitness function, and its specific form will produce different antenna designs as a consequence of the different decision space landscape. Some objective functions may introduce  indirectly as a variable quantity, as is done here through the VSWR; or it may be introduced explicitly as, for example, in the bowtie fitness function in [7], where it is variable, or in the second and third objective functions used in [25], where it is fixed.
indirectly as a variable quantity, as is done here through the VSWR; or it may be introduced explicitly as, for example, in the bowtie fitness function in [7], where it is variable, or in the second and third objective functions used in [25], where it is fixed.
The objective of maximizing IBW is more easily met using Variable 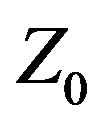 instead of traditional methodology. Var
instead of traditional methodology. Var  is a new, proprietary (patent pending) paradigm for antenna design and optimization methodology that apparently has been heretofore overlooked. For purposes of discussion the term “design” refers to the process of specifying a complete set of parameters defining an antenna meeting specific performance objectives, while “optimization” refers to specifying a complete set of parameters defining the antenna that best meets specific performance objectives. Methodology refers to the methods, techniques, processes, or procedures traditionally used for antenna design and optimization that treat Z0 as a fixed parameter with a constant value that is assigned at the start of the methodology (even if multiple parametric runs are made). Traditional methodology does not consider
is a new, proprietary (patent pending) paradigm for antenna design and optimization methodology that apparently has been heretofore overlooked. For purposes of discussion the term “design” refers to the process of specifying a complete set of parameters defining an antenna meeting specific performance objectives, while “optimization” refers to specifying a complete set of parameters defining the antenna that best meets specific performance objectives. Methodology refers to the methods, techniques, processes, or procedures traditionally used for antenna design and optimization that treat Z0 as a fixed parameter with a constant value that is assigned at the start of the methodology (even if multiple parametric runs are made). Traditional methodology does not consider  a variable quantity whose value is determined by the methodology. This distinction is fundamental and quite important. Traditional methodology excludes from the outset all designs that could provide better performance by using some other value of
a variable quantity whose value is determined by the methodology. This distinction is fundamental and quite important. Traditional methodology excludes from the outset all designs that could provide better performance by using some other value of . The A3 array, for example, was designed against
. The A3 array, for example, was designed against  = 50 Ω resistive, but its performance likely would be better with another value. By treating
= 50 Ω resistive, but its performance likely would be better with another value. By treating  as another design variable in the set of variable antenna system parameters to be determined by the methodology, Var
as another design variable in the set of variable antenna system parameters to be determined by the methodology, Var 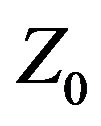 improves on traditional methodology by adding another degree of freedom to the design space or, in the case of optimization, the decision space, thereby making it easier to achieve any particular performance objectives. While Var
improves on traditional methodology by adding another degree of freedom to the design space or, in the case of optimization, the decision space, thereby making it easier to achieve any particular performance objectives. While Var  is especially useful for increasing IBW, it can be used to achieve any performance objectives, including ones not involving IBW.
is especially useful for increasing IBW, it can be used to achieve any performance objectives, including ones not involving IBW.
Besides CFO, any number of other commonly employed algorithms, such as Particle Swarm (PSO) [26], Ant Colony (ACO) [27], Group Search Optimizer (GSO) [28], Differential Evolution (DE) [29-31], or Genetic Algorithm (GA) [32] could be used instead. This “product by process” approach applies to any methodology, deterministic ones like CFO; stochastic metaheuristics like PSO, ACO, GSO, DE or GA; analytic approaches such as extended Wu-King impedance loading [14]; or even “seat of the pants” design or optimization based on experience, intuition, or a “best guess.” The specific design or optimization methodology is irrelevant to the novelty and utility of treating  as a design variable instead of a fixed parameter. Var
as a design variable instead of a fixed parameter. Var 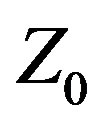 can be used advantageously with any design or optimization methodology.
can be used advantageously with any design or optimization methodology.
4. Results
Figure 3 plots VSWR for the three Yagis, and Table 3 summarizes the bandwidth data for three different VSWR thresholds (2:1, 2.5:1, and 3:1). In the table, 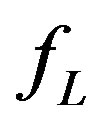 and
and  are the lower and upper frequency limits (MHz) corresponding to VSWRs not exceeding the specified threshold, and
are the lower and upper frequency limits (MHz) corresponding to VSWRs not exceeding the specified threshold, and  is the bandwidth in MHz. The fractional bandwidth in percent relative to the band center frequency
is the bandwidth in MHz. The fractional bandwidth in percent relative to the band center frequency  is computed as
is computed as
 . The CFO-Var
. The CFO-Var 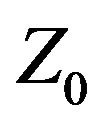 Yagi exhibits
Yagi exhibits
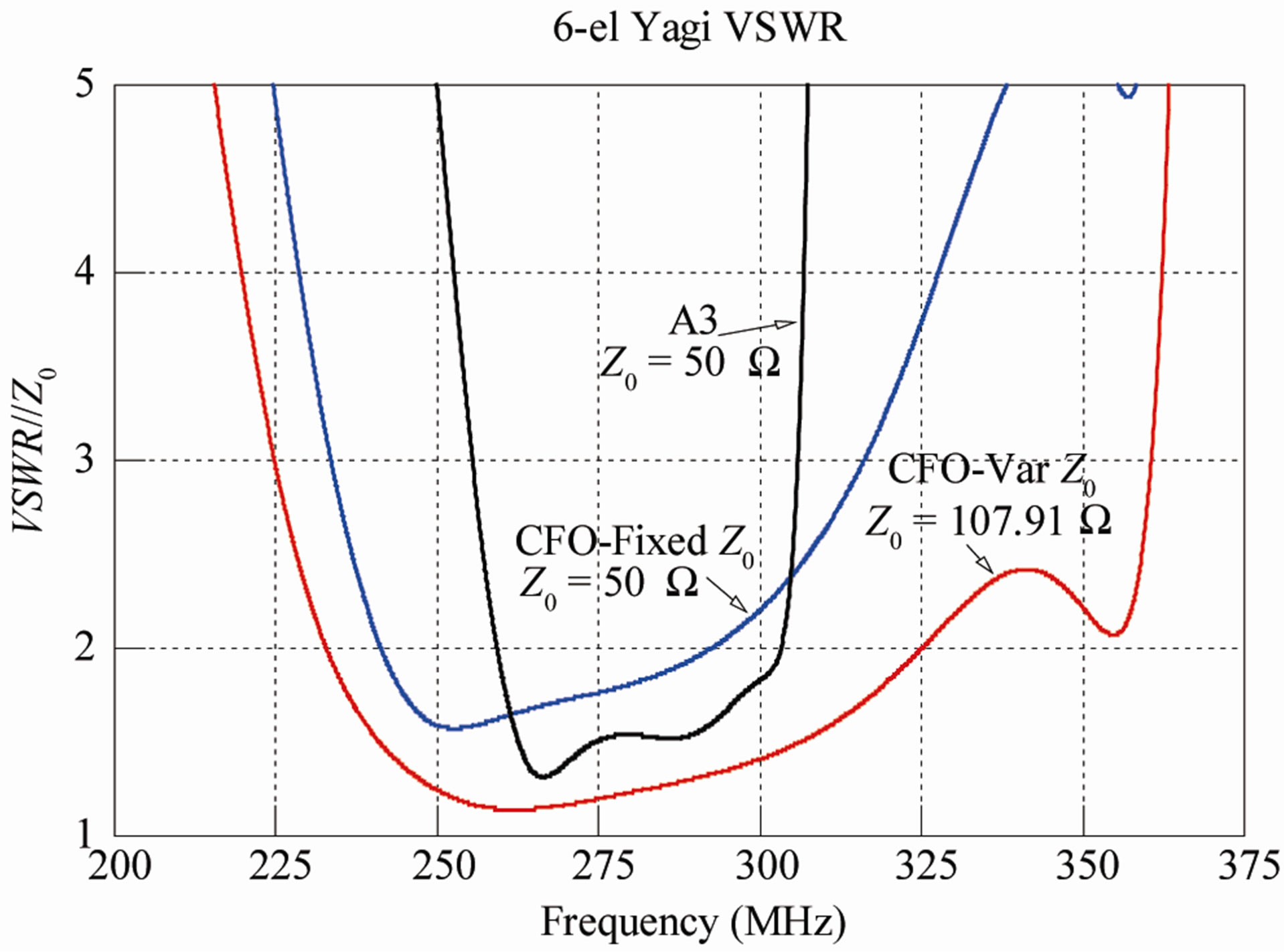
Figure 3. Yagi VSWR relative to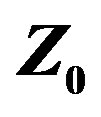 .
.
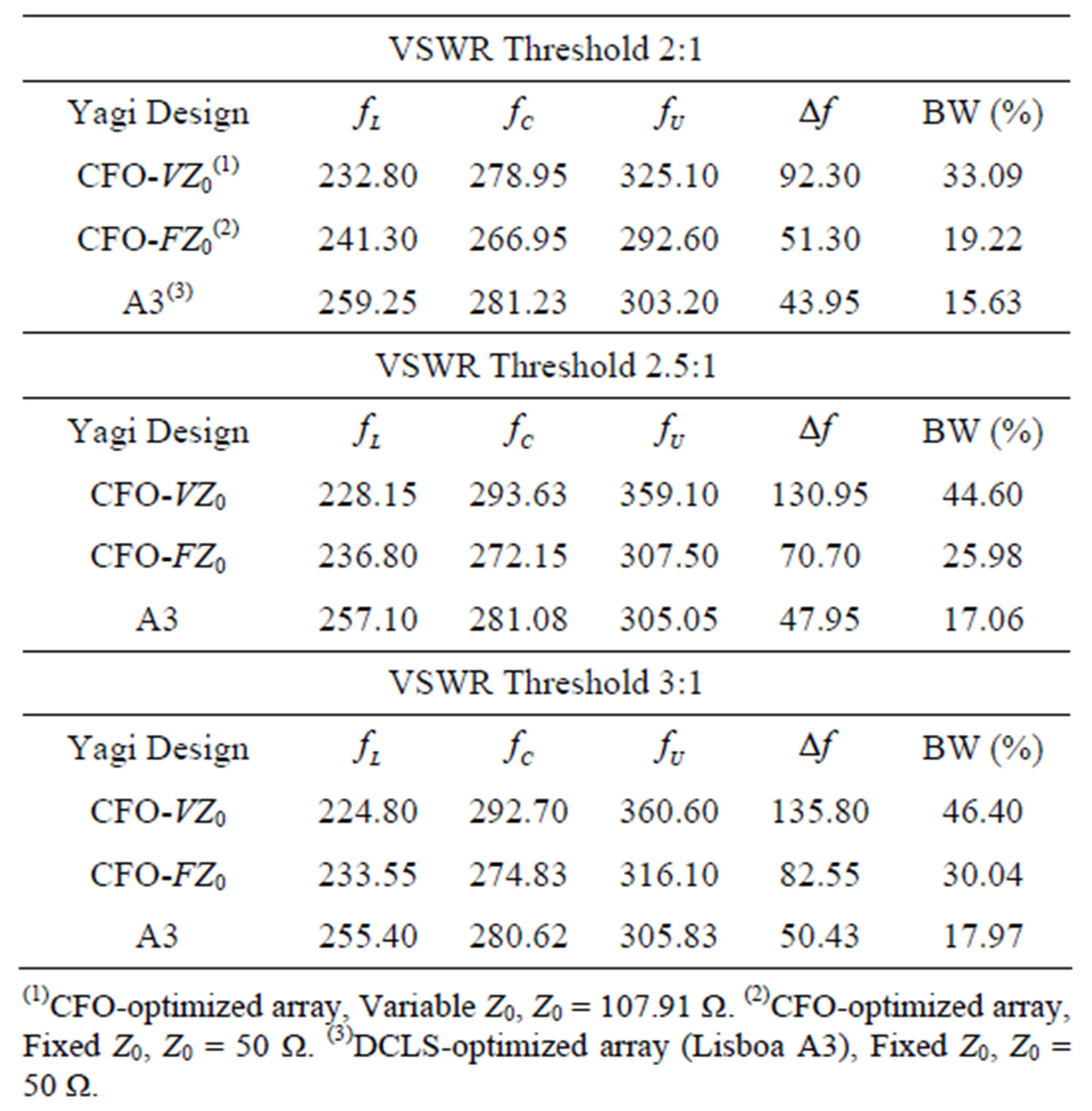
Table 3. 6-el Yagi bandwidth.
UWB performance (fractional bandwidth ≥ 20%) at all VSWR thresholds, whereas the fixed  antenna is UWB at 2.5:1 and above. The Var
antenna is UWB at 2.5:1 and above. The Var  approach increased the Yagi’s VSWR ≤ 2:1 IBW from 19.22% at
approach increased the Yagi’s VSWR ≤ 2:1 IBW from 19.22% at 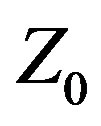 = 50 Ω to 33.09% at
= 50 Ω to 33.09% at 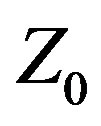 = 107.91 Ω. This improvement is dramatic, and directly attributable to Var
= 107.91 Ω. This improvement is dramatic, and directly attributable to Var  because CFO is a deterministic metaheuristic (the improvement thus cannot be a consequence of an optimizer’s stochasticity). With respect to matching this array to a “standard” 50 Ω feed system impedance, a 2.16:1 impedance ratio broadband transformer or other suitable matching network is required, which easily is accomplished with state-of-the-art matching techniques. By injecting an additional degree of freedom into the traditional antenna design or optimization methodology, Var
because CFO is a deterministic metaheuristic (the improvement thus cannot be a consequence of an optimizer’s stochasticity). With respect to matching this array to a “standard” 50 Ω feed system impedance, a 2.16:1 impedance ratio broadband transformer or other suitable matching network is required, which easily is accomplished with state-of-the-art matching techniques. By injecting an additional degree of freedom into the traditional antenna design or optimization methodology, Var  technology has produced a substantially better antenna than the CFO-optimized traditional fixed
technology has produced a substantially better antenna than the CFO-optimized traditional fixed 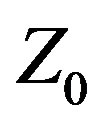 design.
design.
Compared to the CFO-optimized Yagis, the A3 array is considerably more narrowband. Its VSWR ≤ 2:1 IBW is only 15.63%, and it increases only slightly to 17.97% at 3:1. The A3 array’s best IBW performance across all three VSWR thresholds is not as good as the CFO-FZ0 array at its lowest threshold. This is a consequence of the very steep skirts in its VSWR plot. While the CFO-Var  array exhibits similarly steep skirts, as is evident from the plot, its basic IBW is much greater to start.
array exhibits similarly steep skirts, as is evident from the plot, its basic IBW is much greater to start.
Figures 4 and 5 plot forward gain (dBi, decibels relative to isotropic) and front-to-back ratio (FBR), respectively [note that in this case directivity power gain are equal because the PEC array elements result in 100% radiation efficiency]. The CFO-optimized arrays have generally flatter gain curves with moderate gain values compared to the A3 design. While the A3’s gain is higher mid-band, the gain bandwidth is narrow, and the gain falls off precipitously with increasing frequency. Both CFO-optimized arrays also exhibit a substantial decrease in gain at the high end of the band, but the drop off occurs well above the highest frequency with acceptable
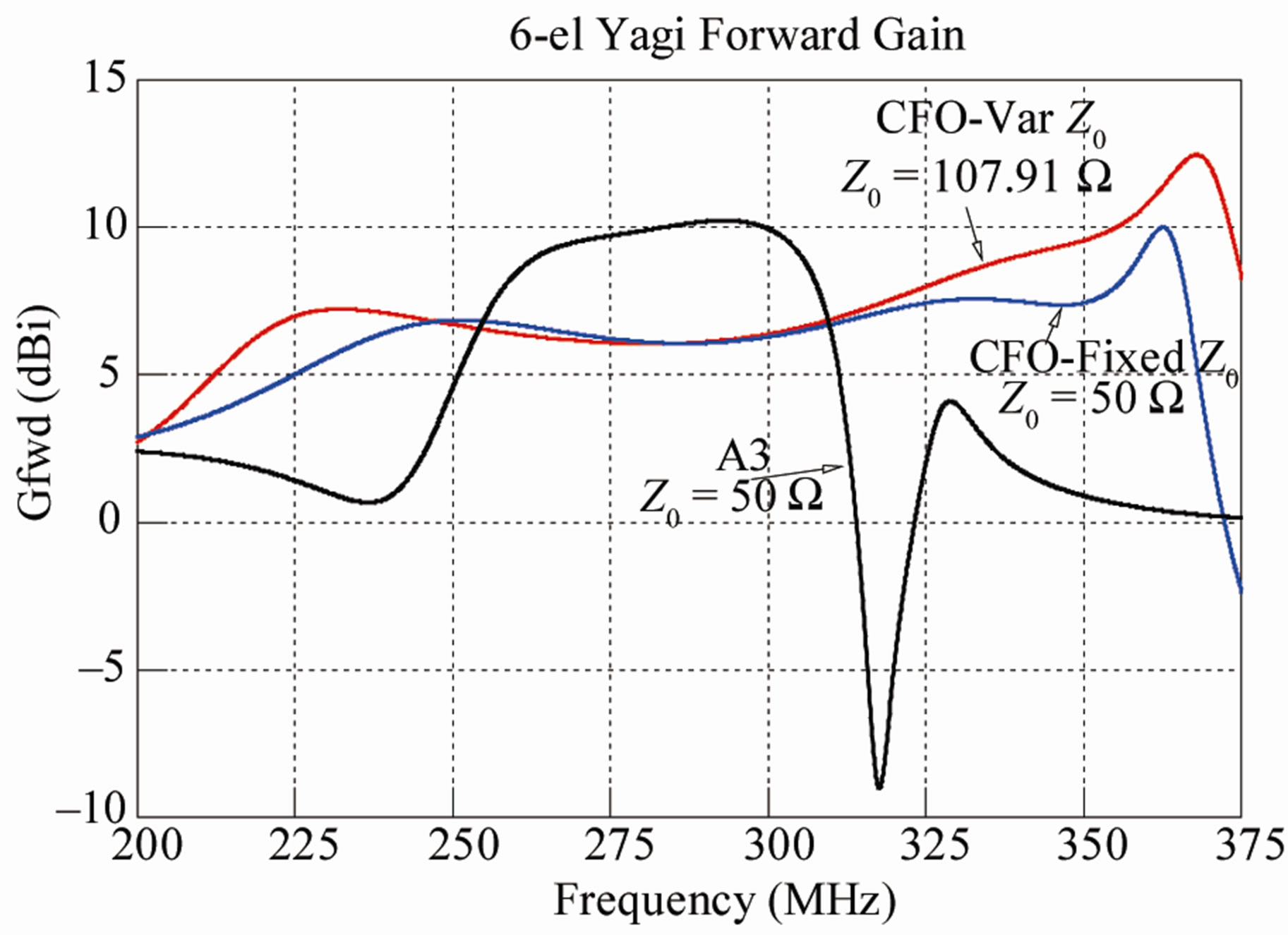
Figure 4. Yagi forward gain.
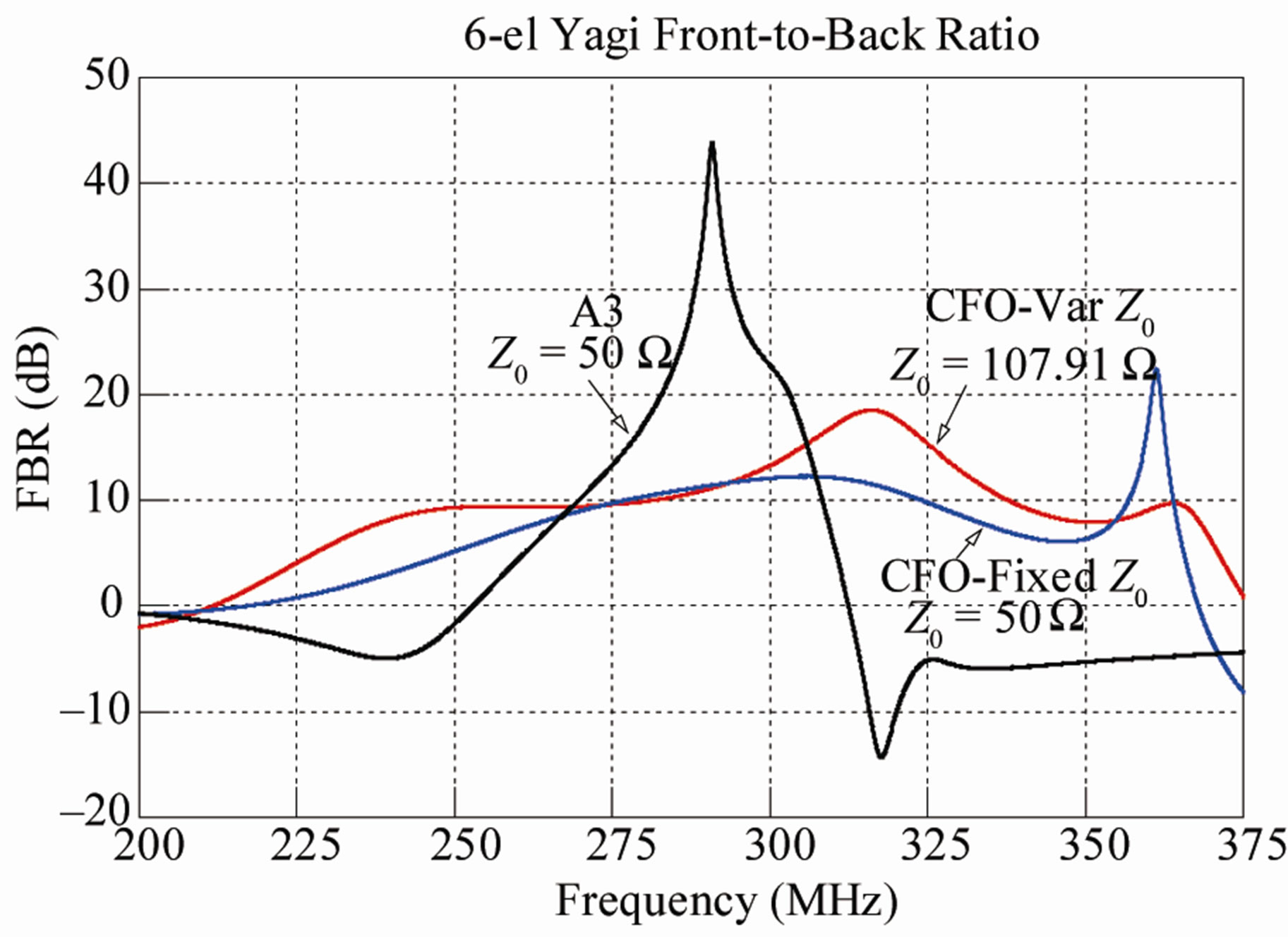
Figure 5. Yagi FBR.
VSWR. The A3 array has a very high mid-band FBR, but only over a fairly narrow range of frequencies. On either side, its FBR decreases sharply and quickly. The CFOoptimized arrays exhibit more moderate FBR values, but over a much greater bandwidth, with the Var 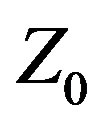 design performing better than its Fixed
design performing better than its Fixed 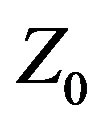 counterpart.
counterpart.
Input resistance and reactance appear in Figures 6 and 7, respectively. The two CFO-optimized arrays exhibit similar behavior for  with moderate values across the band, whereas the A3’s input resistance drops nearly to zero beyond around 310 MHz. For all three antennas, the reactance increases more or less monotonically from about –110 Ω at 200 MHz to between +130 Ω and +130 Ω at 375 MHz. Each Yagi exhibits a single resonance across the entire band.
with moderate values across the band, whereas the A3’s input resistance drops nearly to zero beyond around 310 MHz. For all three antennas, the reactance increases more or less monotonically from about –110 Ω at 200 MHz to between +130 Ω and +130 Ω at 375 MHz. Each Yagi exhibits a single resonance across the entire band.
5. Conclusion
This paper provides an example of applying Central Force Optimization and Variable  technology to the design of a wideband Yagi-Uda array. Even though Yagis are generally considered “narrowband” antennas, the CFO-Var
technology to the design of a wideband Yagi-Uda array. Even though Yagis are generally considered “narrowband” antennas, the CFO-Var 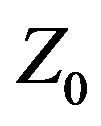 approach produces a Yagi design with good gain and FBR over a fractional bandwidth greater
approach produces a Yagi design with good gain and FBR over a fractional bandwidth greater

Figure 6. Yagi input resistance.

Figure 7. Yagi input reactance.
than 33% with VSWR ≤ 2:1. Variable  is a new approach to antenna design (patent pending) in which the feed system characteristic impedance (or source internal impedance),
is a new approach to antenna design (patent pending) in which the feed system characteristic impedance (or source internal impedance), 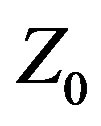 , is treated as a variable quantity whose value is determined by the design or optimization methodology. Variable
, is treated as a variable quantity whose value is determined by the design or optimization methodology. Variable  is a heretofore overlooked and fundamentally different antenna design methodology that departs from the traditional methodology of treating
is a heretofore overlooked and fundamentally different antenna design methodology that departs from the traditional methodology of treating  as a fixed design parameter whose value is specified at the outset and never changes. By introducing into the antenna design or decision space an additional degree of freedom, Variable
as a fixed design parameter whose value is specified at the outset and never changes. By introducing into the antenna design or decision space an additional degree of freedom, Variable  makes it easier to achieve specific performance goals, as illustrated by the Yagi design example. While Variable
makes it easier to achieve specific performance goals, as illustrated by the Yagi design example. While Variable  should be especially useful for improving IBW, it will be useful in achieving any desired antenna performance objectives, even objectives not involving IBW directly.
should be especially useful for improving IBW, it will be useful in achieving any desired antenna performance objectives, even objectives not involving IBW directly.
REFERENCES
- S. Uda, “Wireless Beam of Short Electric Waves,” Journal of the Institute of Electrical Engineers (Japan), March 1926, pp. 273-282.
- H. Yagi, “Beam Transmission of Ultra Short Waves,” P Proceedings of the IEEE, Vol. 85, No. 11, 1928, pp. 1864 -1874.
- C. A. Balanis, “Antenna Theory: Analysis and Design,” Harper & Row, Publishers, New York, 1982.
- The ARRL Antenna Book, 20th Edition, American Radio Relay League, Inc., Newington, 2008.
- A. C. Lisboa, D. A. G. Vieira, J. A. Vasconcelos, R. R. Saldanha and R. H. C. Takahashi, “Monotonically Improving Yagi-Uda Conflicting Specifications Using the Dominating Cone Line Search Method,” IEEE Transactions on Magnetics, Vol. 45, No. 3, 2009, pp. 1494-1497. doi:10.1109/TMAG.2009.2012688
- Federal Communications Commission, “Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems,” First Report and Order, FCC 02-48, Washington DC, 2002.
- R. A. Formato, “A Novel Methodology for Antenna Design and Optimization: Variable Z0 (ver. 2),” 2011. http://arXiv.org/abs/1107.1437
- R. A. Formato, “UWB Array Design Using Variable Z0 Technology and Central Force Optimization, ver. 2,” 2011. http://arXiv.org/abs/1108.0901
- R. A. Formato, “Central Force Optimization: A New Metaheuristic with Applications in Applied Electromagnetics,” Progress in Electromagnetics Research, Vol. 77, 2007, pp. 425-491. doi:10.2528/PIER07082403
- G. M. Qubati, N. I. Dib, and R. A. Formato, “Antenna Benchmark Performance and Array Synthesis Using Central Force Optimization,” Microwaves, Antennas & Propagation, Vol. 4, No. 5, 2010, pp. 583-592, 2010.
- G. Qubati, “Central Force Optimization Method and Its Application to the Design of Antennas,” Masters Dissertation, Jordan University of Science and Technology, Amman, 2010.
- G. M. Qubati, and N. I. Dib, “Microstrip Patch Antenna Optimization Using Modified Central Force Optimization,” Progress in Electromagnetics Research, Vol. 21, 2010, pp. 281-298.
- M. J. Asi and N. I. Dib, “Design of Multilayer Microwave Broadband Absorbers Using Central Force Optimization,” Progress in Electromagnetics Research B, Vol. 26, 2010, pp. 101-113. doi:10.2528/PIERB10090103
- R. A. Formato, “New Techniques for Increasing Antenna Bandwidth with Impedance Loading,” Progress in Electromagnetics Research B, Vol. 29, 2011, pp. 269-288. doi:10.2528/PIERB11021904
- R. A. Formato, “Improved CFO Algorithm for Antenna Optimization,” Progress in Electromagnetics Research B, Vol. 19, 2010, pp. 405-425. doi:10.2528/PIERB09112309
- R. A. Formato, “Parameter-Free Deterministic Global Search with Simplified Central Force Optimization,” In: D.-S. Huang, Z. Zhao, V. Bevilacqua and J. C. Figueroa, Eds., Advanced Intelligent Computing Theories and Applications (ICIC2010), Springer-Verlag, Berlin, 2010, pp. 309-318.
- R. A. Formato, “Central Force Optimization with Variable Initial Probes and Adaptive Decision Space,” Applied Mathematics and Computation, Vol. 217, No. 21, 2011, pp. 8866-8872. doi:10.1016/j.amc.2011.03.151
- R. A. Formato, “Central Force Optimization Applied to the PBM Suite of Antenna Benchmarks,” 2010. http://arXiv.org/abs/1003.0221.
- G. J. Burke, “Numerical Electromagnetics Code—NEC- 4.2 Method of Moments, Part I: User’s Manual,” LLNLSM-490875, Lawrence Livermore National Laboratory, Livermore, 2011.
- G. J. Burke, “Numerical Electromagnetics Code—NEC-4, Method of Moments, Part I: User’s Manual and Part II: Program Description—Theory,” UCRL-MA-109338, Lawrence Livermore National Laboratory, Livermore, 1992.
- G. J. Burke and A. J. Poggio, “Numerical Electromagnetics Code (NEC)—Method of Moments,” Parts I, II and III, UCID-19934, Lawrence Livermore National Laboratory, Livermore, January 1981.
- “4nec2” Antenna Modeling Freeware by Arie Voors, 2005. http://home.ict.nl/~arivoors/
- Unofficial Numerical Electromagnetic Code (NEC) Archives, http://www.si-list.net/swindex.html
- Y. Zehforoosh, C. Ghobadi and J. Nourinia, “Antenna Design for Ultra Wideband Application Using a New Multilayer Structure,” PIERS Online, Vol. 2, No. 6, 2006, pp. 544-549. doi:10.2529/PIERS060531145356
- R. A. Formato, “Issues in Antenna Optimization—A Monopole Case Study,” 2011. http://arXiv.org/abs/1103.5629
- J. Kennedy, and R. Eberhart, “Particle Swarm Optimization,” Proceeding of IEEE Conference on Neural Networks, Vol. 4, 1995, pp. 1942-1948.
- M. Dorigo, V. Maniezzo and A. Colorni, “Positive Feedback as a Search Strategy,” Dipartimento di Elettronica, Politecnico di Milano, Italy, Technical Report 91-016, 1991. http://iridia.ulb.ac.be/~mdorigo/pub_x_subj.html
- S. He, Q. H. Wu, and J. R. Saunders, “Group Search Optimizer: An Optimization Algorithm Inspired by Animal Searching Behavior,” IEEE Trans. Evol. Computation, Vol. 13, No. 5, 2009, pp. 973-990.
- R. Storn and K. V. Price, “Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces,” Technical Report TR-95- 012, ICSI (Univ. of California, Berkeley), 1995. http://www.icsi.berkeley.edu/~storn/litera.html
- R. Storn and K. V. Price, “Minimizing the Real Functions of the ICEC 1996 Contest by Differential Evolution,” Proceedings of 1996 IEEE International Conference on Evolutionary Computation, Nagoya, 20-22 May 1996, pp. 842-844. doi:10.1109/ICEC.1996.542711
- A. Chowdhury, A. Ghosh, R. Giri and S. Das, “Optimization of Antenna Configuration with a Fitness-Adaptive Differential Evolution Algorithm,” Progress in Electromagnetics Research B, Vol. 26, 2010, pp. 291-319. doi:10.2528/PIERB10080703
- E. A. Jones and W. T. Joines, “Design of Yagi-Uda Antennas Using Genetic Algorithms,” IEEE Transactions on Antennas and Propagation, Vol. 45, No. 9, 1997, pp. 1386-1392. doi:10.1109/8.623128
NOTES
1Variable Z0, V Z0, and Var Z0 are trademarks and service marks of Massachusetts Corporation Variable Z0, Ltd., P.O. Box 1714, Harwich, MA 02645 USA.

