Smart Grid and Renewable Energy
Vol.06 No.06(2015), Article ID:57492,13 pages
10.4236/sgre.2015.66015
Power Quality Issues Concerning Photovoltaic Generation and Electrical Vehicle Loads in Distribution Grids
Jaan Niitsoo1, Paul Taklaja1, Ivo Palu1, Joni Klüss2
1Department of Electrical Power Engineering, Tallinn University of Technology, Tallinn, Estonia
2Department of Electrical Engineering and Automation, Aalto University, Helsinki, Finland
Email: jaan.niitsoo@ttu.ee
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 May 2015; accepted 26 June 2015; published 29 June 2015
ABSTRACT
The high utilization level of renewable generation including residential photovoltaic (PV) systems together with the uncontrolled charging of electric vehicles (EVs) can have a significant impact on load characteristics in distribution networks. Harmonic content of PV generation, EV charging loads, and their influence on power quality indicators in residential distribution networks are discussed in this paper. For investigating likely power quality scenarios, PV generation and EV charging measurement results including current harmonic amplitude and phase angle values are used and compared with present load characteristics. Different modelling scenarios are analysed and a simplified model of harmonics in PVs and EVs is offered. The results of the study show moderate additional harmonic distortion in residential load current and voltage distortion at the substation’s busbar when PV generation and EV loading are added. The scenarios presented in this paper can be further used for modelling the actual harmonic loads of the PVs and EVs in distribution networks.
Keywords:
Current Measurement, Distributed Generation, Electric Vehicles, Load Modelling, Photo Voltaic, Power Quality, Power System Harmonics

1. Introduction
Power distribution networks are designed to operate with sinusoidal voltage. The deviation of the actual voltage waveform from an ideal sine wave is a fundamental aspect related to power quality. This deviation can be described as a sum of harmonic voltage components. A higher level of harmonics correlates to larger distortion. From the point of view of electromagnetic compatibility, harmonics must be kept within given compatibility levels to enable satisfactory operation of all equipment supplied by the network. Furthermore, since electricity is also defined as a product, utility companies could be held responsible for excessively high harmonic levels and any resulting damage to customers’ property [1] .
The appliances and electric devices connected to the public power supply network are also designed to operate with a sinusoidal voltage at rated power. However, many of the connected loads are nonlinear, meaning that they draw current with a distorted sine waveform. It has been estimated that already in 2012, 60% of the power system loads in USA were nonlinear loads [2] . Nonlinear current in turn provides nonsinusoidal voltage drop, thus resulting in distorted network voltage. In particular, distortion levels may increase significantly when numerous harmonic emitting devices are utilized in bulk [3] .
Distorted voltage and current may result in undesirable effects not only for the distribution system, but also for the customers. Nonlinear loads inject harmonic currents and induce increased voltage drops over both phase and neutral conductors [4] . As a result, potential damage to sensitive electronic equipment and capacitor banks, overheating of transformers and neutral conductors, and additional losses in the power system are likely. Degraded power quality entails additional costs for both the electricity distributor and its customers as these effects cause premature aging and failure in power system devices [5] - [7] .
Advances in power electronics has led to the widespread use of switching converters for the general public use as well as industrial applications. Power electronic converters draw non-sinusoidal current from the grid and this has led to a rapid increase in the number of nonlinear loads. In addition to the increased number of electronic devices, also resistive devices such as incandescent lamps are ever more frequently replaced by energy saving lamps utilizing nonlinear elements. Depending on type and brand, switching power supplies absorb distorted currents which flow through the impedances of the power distribution system and result in distortion of system bus voltage [8] .
Similarly, modern EV chargers employ switching power converters. Due to the high energy requirement of the EV, charging at home can use power levels very close to the ones of the actual residential customers drawing, 10 - 15 A [9] . The charging of EVs produces considerable additional power electronic load which can generate harmonics and result in associated power quality issues in residential networks.
Power electronics is also implemented in residential photovoltaic (PV) generators, which is currently the dominant renewable energy source in urban and metropolitan areas. The inverters required to supply households from the PVs are nonlinear power supplies, meaning that they provide distorted waveform outputs that increase the levels of harmonics. This technology is enjoying rapid growth due to a combination of subsidies, the abundance of sunshine, and the low impact of the technology on the urban landscape [5] .
The present study identifies and analyses possible power quality scenarios in a residential distribution network by examining the impact of nonlinear domestic loads such as EVs and PV inverters. Measured power consumption and current waveforms of different home appliances, EVs and PV inverter have been used for the analysis. All loads considered in the model were provided with magnitudes and phase angles of each harmonic up to the 50th order. The main purpose of this paper is to present the use of actual measurement data from different devices for modelling the effects on the residential distribution network and give an estimation of the important values for further modelling.
2. Theoretical Background
In electrical power networks, a non-sinusoidal periodic waveforms can be presented as a sum of numerous harmonic components (harmonics), each having an integer-multiple frequency of the main frequency. Different waveforms have different harmonic content, referring to different patterns of individual harmonic magnitudes and phase shift compared to the main frequency component. Hereafter in this paper, the presented measurements of loads are all indicated as magnitudes and phase shift of each individual harmonic up to the 50th order.
Distortions can be observed individually by comparing different harmonic components and calculating harmonic distortion (HD). A more general approach to quantifying the distortions is using the total harmonic distortion level (THD). Total harmonic distortion can be expressed separately for current harmonic distortion as THDI and for voltage distortion as THDU. The total harmonic distortion indicators can be calculated using corresponding Equations (1) and (2),
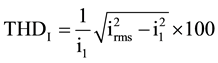 (1)
(1)
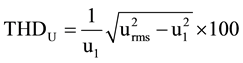 (2)
(2)
where i1 is current of 1st order and u1 is voltage of 1st order.
THD does not reveal the magnitudes of individual harmonics, which could still exceed the limits for specific harmonics regardless of THD value. For the correct estimation of the harmonic levels, calculations have to make use of magnitude and phase angle values of individual harmonics. Harmonic phase angle diversity is relevant when multiple appliances are operating simultaneously, creating either reinforcement or cancellation of harmonic magnitudes [2] . It is reported that 10% smaller harmonic current magnitudes can be seen when phase angle information is included compared to the simple summing of magnitudes without phase angle values [10] . The attenuation effect is dependent only on the phase angle, but the effect’s severity is dependent on the magnitude of the harmonic voltage [11] .
The combined influence of harmonics from different sources is highly dependent on network topology, mutual conductor impedances and phase balance. The resulting harmonic distortion in the distribution network can increase or decrease due to the variation of phase angles for different harmonic sources. A special situation occurs in the case of a balanced three phase load consisting of identical nonlinear loads. Since the triplen harmonics sum in neutral, the three phase supply system neutral conductor total current can be higher than the phase current [4] [12] . For example in the Netherlands and in Denmark, analysis has shown that the 15th harmonic current, which is one of the triplen harmonics, has exceeded the tolerable limits in several cases [12] . Therefore, phase balance is a significant factor for harmonic emission in distribution networks [7] .
The harmonic generation of a PV system depends on the inverter technology, and operation conditions, including solar irradiance, temperature, loads, and the supply system characteristics. Both the current THD and the output reactive power are related to the output active power levels, which in turn are strongly dependent on solar irradiance levels. Most of the inverters consume or feed reactive power into the network depending on their output active power and their technology. During operation at low solar irradiance levels (e.g. sunrise, sunset, cloudy days), current THD values can increase rapidly since the THD factor is inversely proportional to the output active power of the PV inverters. Nevertheless, THD is notably reduced as the output active power of the PV inverters increases and reaches its nominal value [13] - [15] .
Varying power density of renewable energy not only potentially cause supply voltage sag or swell patterns but also frequency variations in the LV grids. The application of power converters as interfaces between energy sources and the LV grid and their interaction with other system components may cause high harmonics distortion [16] [17] . The effects of the nonlinear residential load on voltage THD are most significant on a local level, and equipment failures due to voltage distortion are more likely to occur along distribution feeders than farther upstream. The results show that recommended voltage THD limits can easily be exceeded, particularly at nearby distribution feeder tap points, if the loading equipment is highly nonlinear [18] .
EV batteries require DC for charging, but all uncontrolled rectifiers inject a high content of current harmonics into AC power networks. Based on literature, it can be concluded that over time and with the development of power supply technologies, the amount of distortion from EV charging has decreased. Measurements in the 1990’s showed that the use of uncontrolled or low-control rectifiers caused average current THD of 50% [19] . Measurements of modern commercial EVs have indicated an average charging current THD around 11%…12% [20] [21] , but values as low as 4.5% [22] have also been indicated.
Monitoring of 100 distribution network feeders in USA revealed that the average voltage THD at PCC (Place of Common Coupling) was 4.73% [23] . It may be assumed that the stated percentage is quite common for many distribution grids. Power supply standards (EN50160) have set the upper voltage THD limit for public networks at 8% [24] . Nevertheless, severe cases have been revealed where distortion has been higher than 17% [25] .
3. Methods
The 50 Hz residential distribution network at 0.4 kV and loads for assessing load flow were modelled using DIgSILENT Power Factory software. The model consisted of a three-phase residential load at 0.4 kV voltage level composed of different single phase loads. The schematic of the residential load model is presented in Figure 1.
Figure 1. Schematic of residential load model.
The compiled residential load was connected to the distribution network substation via a 1.4 km long 4 × 95 mm2 overhead line (OHL) as depicted on Figure 2 and it is the only consumer of this substation. The distribution network substation was connected to a 10 kV network with short-circuit power of 200 MVA and short-cir- cuit current 11.5 kA. The high voltage (HV) busbar is modelled as a slack bus. The transformer used in the distribution substation was modelled with the following parameters:
nominal power 25 kVA;
relative short circuit voltage 4.5%;
zero sequence impedances r0 = 0.02 pu and x0 = 0.04 pu;
magnetizing impedance/short circuit impedance ratio 3;
vector group Yyn.
Implemented parameters in the simulation were selected based on power quality problematic issues identified in Elektrilevi’s network (Estonia’s main distribution grid operator) for July 1, 2013. The length of the OHL between substation and customer’s PCC was defined as an average of all the lines between substations and customers with power quality problems. Similarly, the selected diameter of the line and nominal power of the transformer are the most common values for the identified problematic components.
Harmonic voltage amplitudes and phase angles up to the 50th order were obtained from measurements conducted by Elektrilevi at one of the sites where power quality issues were identified. Harmonic voltage distortion at the 10 kV bus was measured and modelled around 2%, which is a common value for this grid.
For modelling PV generation, one single phase PV was measured for one week. For modelling EV loads, actual charging process of five different EVs were measured. All vehicles were produced in 2012-2013 and are commercially available on the markets. In each case, harmonic current amplitudes and phase angles up to 50th order were measured and used in the models in DIgSILENT. Both PV and EV were connected to residential load’s busbar as was described in Figure 1. Also a mean load model of averaged values was composed for the single phase PV system and EV.
In order to model the network response of nonlinear loads, 14 different home appliances were measured. The results of the corresponding measured active and reactive power, harmonic current magnitudes and harmonic current phase shift angles of measured devices are presented in [26] [27] . Modelled devices were arranged in a manner where similar active power consumption was seen in every phase. In the model, all nonlinear devices are in operation and coincidence factors are not taken into account, thus representing the presumed worst case scenario.
4. Results
Three cases modelling the residential distribution network are presented. Initial conditions represent the loads common to present day households.
1) First case: one single-phase PV unit connected to the PCC in addition to the initial load.
2) Second case: one EV charging load connected to the PCC in addition to the initial load.
3) Third case: EV charging load and PV inverter are connected to the PCC in addition to the initial load.
Figure 2. Schematic of distribution grid model.
Initial values of voltage and current in the grid before adding PV generations or EV load are presented in Table 1. Voltage THD and power factor (PF) values are listed in Table 2 and power values are listed in Table 3.
A) First Case―Single Phase PV
Measurement results for three different power levels (1―near 30%, 2―near 60%, 3―near 100%) of the single phase PV are given in Table 4. From the table, it can be assumed that current distortion is slightly correlated with current and decreases as current increases. Also voltage and voltage distortion variations may somewhat have an effect on the current distortion, but are here ignored due to very low values of voltage THD and the fact that current itself is more affected by voltage. The same conclusion can be made by observing the power factor (PF) value which approaches unity with increasing current. Interestingly in this case, reactive power Q appears to be independent of the current level and changes polarity.
Voltage and current distortion during a 15 h period is shown in Figure 3. Voltage distortion at the measurement point was notably low (around 1%) throughout the observed time period and similarly, current distortions are not greatly affected by grid disturbances.
Power quality indexes are illustrated in Figure 4. Results are in line with the prior conclusion for reactive power where Q is mainly capacitive throughout the measurement period. It can also be confirmed that reactive power is independent of current (compare with active power P and apparent power S).
As is evident in Figure 5, cos(φ) remained near unity throughout the measurement period, whereas PF varied considerably. The observed fluctuations in PF are a result of current distortion which is evident when comparing the current THD (THD_I in Figure 3) with the PF curve in Figure 5.
Table 5 and Table 6 present the harmonic currents and phase angles up to the 21st order for the single phase PV inverter with the corresponding power levels (1―near 30%, 2―near 60%, 3―near 100%) described in Table 4. Average values are also calculated and presented for modelling mean one phase PV. Even and higher order harmonics are left out due to their marginal dimension. All presented harmonic current amplitudes exhibited relatively moderate values, except for the third harmonic which was more notable.
For modelling mean PV generation, average values of the presented current harmonic amplitudes and angles (Table 5 and Table 6) were calculated. Main frequency current phase angles were defined zero as in the ideal case and other angles were calculated in relation to mains current. Figure 6 shows a graphical representation (vector quadrant) of the calculated average harmonics, where X and Y components of current are calculated using Formulas (3) and (4). Where A is mean harmonic (3rd, 5th, 7th etc. order) current in percentages to main frequency current and α is mean harmonic (3rd, 5th, 7th etc. order) current angle in degrees to main frequency current.
 (3)
(3)
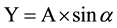 (4)
(4)
A single phase PV inverter was connected to the residential busbar at different phases one at a time. The resulting voltages and currents are presented in Table 7. Voltage THD and PF is shown in Table 8 and power values are displayed in Table 9.
As it can be seen from Table 7 voltage in the phase where the PV is connected rises more than 5%. Significant voltage THD rise due to the connected PV could not be seen. Instead, THD decreased slightly in cases where PV was connected to phase A and C as evident in Table 8. Due to the change in reactive power, seen in Table 9, the PF value changed in the phase where the PV was installed.
Figure 3. Measured voltage THD and current THD of single phase PV inverter.
Figure 4. Measured power values of single phase PV inverter.
Figure 5. Measured power factors of single phase PV inverter.
Table 1. Initial modelled voltage [V] and current [A] values.
Table 2. Initial modelled voltage THD [%] and PF values.
Figure 6. Mean harmonic current vectors (from 3rd to 21st order) in percentages compared to fundamental harmonic current vector (1st order) values of single phase PV inverter.
Table 3. Initial modelled active [kW] and reactive power [kvar] values.
Table 4. Measured values for single phase PV inverter.
Table 5. Harmonic currents of single phase PV inverter.
Table 6. Harmonic current phase angles of single phase PV inverter.
Table 7. Modelled voltage [V] and current [A] values for first case.
Table 8. Modelled voltage THD [%] and PF values for first case.
Table 9. Modelled active [kW] and reactive power [kvar] values for first case.
B) Second Case―EV
Measurements were recorded for the charging of five different EVs. Power and THD values while EVs were charging at constant power level are presented in Table 10. As the power values (P and Q) were quite similar for all five EVs, the current distortion varied more. Three EVs out of five had current distortion around 10%…12% and two had substantially lower values, around 3%…4%.
The characteristics of individual current harmonic magnitudes and phase angles for odd harmonics during the constant power charging are presented in Table 11 and Table 12. The highest current amplitudes were observed at 3rd, 5th, 7th and 13th orders. For successful modelling, the mean values based on five EVs were calculated. The arithmetic mean of amplitudes (AM) and geometric mean for phase angles (GM) was calculated as follows:
Table 10. General data for EVs during constant power charging time.
Table 11. Harmonic current amplitudes [%] of EVs.
Table 12. Harmonic current phase angles [˚] of EVs.


The most significant individual harmonics (3rd and 5th) are illustrated in Figure 7 and Figure 8. As evident from the figures, the directions of the currents are different.
In this case, mean EV was added to the grid at the residential busbar at different phases one at a time. The resulting voltages and currents are shown in Table 13, voltage THD and PF in Table 14 and power values in Table 15.
The EV load causes voltage drop in phase where it is connected more than 5% in each case. Voltage THD was observed to increase up to 0.5% in two cases, but remained at same level when EV was connected to phase C. Power factor changed slightly due to additional EV load and slightly improved in the phase where it was connected.
Figure 7. Third current harmonics of EVs.
Figure 8. Fifth current harmonics of EVs.
Table 13. Modelled voltage [V] and current [A] values for second case.
Table 14. Modelled voltage THD [%] and PF values for second case.
Table 15. Modelled active [kW] and reactive power [kvar] values for second case.
C) Third Case―PV and EV
In this case, a PV and EV where both installed at the residential load’s busbar. To investigate differences in harmonic cancellation, the PV and EV were installed both on the same phases as well as separate phases.
Voltages and currents are presented in Table 16. It was observed that in arrangements where PV and EV are in same phase voltage drops near to undesirable levels in the phase where the EV is connected while increasing over the 10% limit in the phase where the EV is connected. Also in those cases neutral currents rise much higher than phase currents. The best practice is to install both in same phase. Voltages over the 10% limit and high neutral currents are marked as bold in Table 16.
Voltage THD and PF values are presented in Table 17. In the worst case (EV in A and PV in C), voltage THD decreases in one phase up to 0.6%, but placing EV and PV both on the same phase can lead to slightly decreased voltage THD in some situations (EV in C and PV in C).
Placing the devices onto the same phase leads to slight growth of reactive power in the same phase as evident in Table 18. Active power is compensated due to opposite direction of power flow of the EV and PV.
5. Discussion
While the discreet disturbances of harmonic distortion may not cause immediate and easily-observed impacts, it can cause some equipment to malfunction, and result in additional power losses in both customer and network equipment [28] . As harmonic levels change considerably from one week to another, it is very difficult to assess the long-term evolution of harmonic levels only from measurements carried out over a short period [1] . This paper clearly concludes that power quality problems may occur when dispersed generation and powerful non- linear load utilization is not sufficiently considered. Moreover, modern household devices tend to contain more power electronic circuits and therefore an increase of harmonic currents can also be expected even without the PVs or EVs.
Harmonic current angles of small generators such as PVs or powerful nonlinear loads such as EVs are seldom considered. For determining the impact of current harmonics on the network and the voltage harmonics, the actual harmonic current values would have to be used. One aim of this paper is to draw attention to this topic which could lead to advances in modelling nonlinear generations and loads with different topologies. To help mitigate harmonic distortion problems, models with appropriate harmonic current amplitudes and phase angles could be used to select most suitable devices.
Table 16. Modelled voltage [V] and current [A] values for third case.
Table 17. Modelled voltage THD [%] and PF values for third case.
Table 18. Modelled active [kW] and reactive power [kvar] values for third case.
This study only examines one household and one PV or EV at time. The described effects may escalate when a larger number of devices are considered. Special attention is needed in situations where devices have similar harmonic patterns and the harmonic cancellation effect is minimal and grid is weak. General values for further modelling of PVs and EVs were presented in this paper, but additional measurements should be performed to obtain unified values for modelling PV generators and EV loads more accurately. It would be necessary to have measurement data extending over entire years in order to acquire results independent of any disturbance. Furthermore, flicker and voltage level issues should be accounted for as they may have a significant influence in real applications.
6. Conclusions
Firstly, it can be concluded that current harmonic distortion of the PV’s output is notably correlated with current and distortion decreases when the PV is operating at a higher loading level. The same conclusion can be made by observing the PF value of the PV which approaches unity with increasing current. Whereas when PF varied considerably, cos(φ) remained near unity throughout the measurement period, which means that main order reactive power is compensated more efficiently than higher order reactive power. EVs showed higher current distortions than PV. Three EVs out of five had current distortion around 10%…12% and two had substantially lower values, around 3%…4%.
Voltage distortion may rise when PVs and EVs are connected to a residential load. The rise is much dependant on grid strength and worse situation may occur in cases where less powerful transformers and thinner cables are utilized. The present study showed that most reasonable option is to connect both PV and EV on same phase. Installing the EVs and PVs separately or installing both on separate phases, results in notable increase in voltage distortion.
Even more severe changes occurred with voltage amplitudes and neutral currents. In cases where PV and EV both were installed, voltage in the phases where PV was connected rose over the 10% limit. Also the neutral currents rose nearly two times higher than phase currents where PV and EV where connected in separate phases. It concludes that modelling with different transformer powers and cable lengths and thicknesses should be conducted before installing nonlinear devices.
References
- Berthet, L., Eyrolles, P., Gauthier, J. and Sabeg, S. (2007) Harmonic Level Measurements on French Low-Voltage Networks. 19th International Conference on Electricity Distribution, Vienna, 21-24 May 2007.
- Rawa, M.J.H., Thomas, D.W.P. and Sumner, M. (2011) Simulation of Non-Linear Loads for Harmonic Studies. 11th International Conference on Electrical Power Quality and Utilisation (EPQU), Lisbon, 17-19 October 2011, 1-6. http://dx.doi.org/10.1109/EPQU.2011.6128915
- Niitsoo, J. and Palu, I. (2011) Distorted Load Impacts on Distribution Grid. Proceedings of the 12th International Scientific Conference Electric Power Engineering 2011, Kouty nad Desnou.
- Desmet, J., Debruyne, C., Vanalme, J. and Vandevelde, L. (2010) Power Injection by Distributed Generation and the Influence of Harmonic Load Conditions. IEEE Power and Energy Society General Meeting, Minneapolis, 25-29 July 2010, 1-6. http://dx.doi.org/10.1109/pes.2010.5590123
- Jayasekara, N. and Wolfs, P. (2010) Analysis of Power Quality Impact of High Penetration PV in Residential Feeders. 20th Australasian Universities Power Engineering Conference (AUPEC), Christchurch.
- Renders, B., Degroote, L., Driesen, J. and Vandevelde, L. (2007) Profits of Power-Quality Improvement by Residential Distributed Generation. 42nd International Universities Power Engineering Conference, Brighton, 4-6 September 2007, 377-381. http://dx.doi.org/10.1109/upec.2007.4468976
- Arghandeh, R., Onen, A., Jung, J. and Broadwater, R. (2013) Harmonic Interactions of Multiple Distributed Energy Resources in Power Distribution Networks. Electric Power Systems Research, 105, 124-133. http://dx.doi.org/10.1016/j.epsr.2013.07.018
- Aiello, M., Cataliotti, A., Favuzza, S. and Graditi, G. (2006) Theoretical and Experimental Comparison of Total Harmonic Distortion Factors for the Evaluation of Harmonic and Interharmonic Pollution of Grid-Connected Photovoltaic Systems. IEEE Transactions on Power Delivery, 21, 1390-1397. http://dx.doi.org/10.1109/TPWRD.2005.860231
- Shao, S.P.M. (2011) Demand Response as a Load Shaping Tool in an Intelligent Grid with Electric Vehicles. IEEE Transactions on Smart Grid, 2, 624-631. http://dx.doi.org/10.1109/TSG.2011.2164583
- Kütt, L., Saarijärvi, E., Lehtonen, M. and Niitsoo, J. (2013) A Review of the Harmonic and Unbalance Effects in Electrical Distribution Networks Due to EV Charging. 13th International Conference on Environment and Electrical Engineering (EEEIC), Wroclaw.
- Yong, J., Chen, L. and Chen, S. (2010) Modeling of Home Appliances for Power Distribution System Harmonic Analysis. IEEE Transactions on Power Delivery, 25, 3147-3155. http://dx.doi.org/10.1109/TPWRD.2010.2051960
- Jensen, M.M. and Hansen, H. (2014) Triplen Harmonic Voltage Distortion in the Low-Voltage Network. NORDAC 2014, Stockholm.
- Block, P., Salamanca, H., Teixeira, M., Dahlke, D., Shiono, O. and Dodadon, A. (2014) Power Quality Analyses of a Large Scale Photovoltaic System. The fifth International Renewable Energy Congress IREC 2014, Hammamet, 25-27 March 2014, 1-6. http://dx.doi.org/10.1109/irec.2014.6826946
- Kontogiannis, K., Vokas, G., Nanou, S. and Papathanassiou, S. (2013) Power Quality Field Measurements on PV Inverters. International Journal of Advanced Research in Electrical Electronics and Instrumentation Engineering, 2, 5301-5314.
- Ortega, M., Hernández, J. and García, O. (2013) Measurement and Assessment of Power Quality Characteristics for Photovoltaic Systems: Harmonics, Flicker, Unbalance, and Slow Voltage Variations. Electric Power Systems Research, 96, 23-35. http://dx.doi.org/10.1016/j.epsr.2012.11.003
- Anwari, M., Hamid, M. and Taufik (2008) Power Quality Behavior of Single Phase Fed Adjustable Speed Drive Supplied from Grid of PV Generation. The 2nd IEEE International Conference on Power and Energy (PECon 08), Bahru, 1-3 December 2008, 1098-1102.
- van Lumig, M., Bhattacharyya, S., Gobben, J. and Kling, W. (2010) Power Quality Measurements Near DER and Disturbing Loads. International Conference on Renewable Energies and Power Quality (ICREPQ’11), Las Palmas de Gran Ganaria, 13-15 April 2010.
- Wang, Y.J., O’Connell, R. and Brownfield, G. (2001) Modeling and Prediction of Distribution System Voltage Distortion Caused by Nonlinear Residential Loads. IEEE Transactions on Power Delivery, 16, 744-751. http://dx.doi.org/10.1109/61.956765
- Berisha, S., Karady, G., Ahmad, R., Hobbs, R. and Karner, D. (1996) Current Harmonics Generated by Electric Vehicle Battery Chargers. Proceedings of the 1996 International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, 8-11 January 1996, 584-589.
- Zamri, M., Wanik, C., Fadzil, M., Siam, M., Ayob, A., Yanto, S., Azah, M., Azit, A., Sulaiman, S., Azrin, M., Ali, M., Hussein, Z.F., Kamil, A. and Hussin, M. (2013) Harmonic Measurement and Analysis during Electric Vehicle Charging. Engineering, 5, 215-220.
- Melo, N., Mira, F., de Almeida, A. and Delgado, J. (2011) Integration of PEV in Portuguese Distribution Grid: Analysis of Harmonic Current Emissions in Charging Points. 11th International Conference on Electrical Power Quality and Utilisation (EPQU), Lisbon, 17-19 October 2011, 1-6. http://dx.doi.org/10.1109/EPQU.2011.6128893
- Wenge, C., Stotzer, M., Winkler, T. and Komarnicki, P. (2011) Power Quality Measurements of Electric Vehicles in the Low Voltage Power Grid. 11th International Conference on Electrical Power Quality and Utilisation (EPQU) Lisbon, 17-19 October 2011, 1-5. http://dx.doi.org/10.1109/EPQU.2011.6128866
- Fekete, K., Klaic, Z. and Majdandzic, L. (2012) Expansion of the Residential Photovoltaic Systems and Its Harmonic Impact on the Distribution Grid. Renewable Energy, 43, 140-148. http://dx.doi.org/10.1016/j.renene.2011.11.026
- McBee, K. and Simoes, M. (2012) Evaluating the long-Term Impact of a Continuously Increasing Harmonic Load Demand on Feeder Level Voltage Distortion. 2012 IEEE Industry Applications Society Annual Meeting (IAS), Las Vegas, 7-11 October 2012, 1-8. http://dx.doi.org/10.1109/IAS.2012.6374086
- Au, M.T., Navamany, J. and Yeoh, E.C. (2010) Impact of Medium Power Inverter-Based Residential Harmonic Loads and PFCs on Low Voltage Lines. 2010 IEEE International Conference on Power and Energy (PECon), Kuala Lumpur, 29 November-1 December 2010, 695-699. http://dx.doi.org/10.1109/pecon.2010.5697669
- EN 50160:2010 (2010) Voltage Characteristics in Public Distribution Systems. European Standard.
- Niitsoo, J., Kilter, J., Palu I., Taklaja, P. and Kütt, L. (2013) Harmonic Levels of Domestic and Electrical Vehicle Loads in Residential Distribution Networks. Proceedings of AFRICON 2013, Mauritius, 9-12 September 2013, 1-5. http://dx.doi.org/10.1109/AFRCON.2013.6757800
- Niitsoo, J., Palu, I., Kilter, J., Taklaja, P. and Vaimann, T. (2013) Residential Load Harmonics in Distribution Grid. Proceedings of 3rd International Conference on Electric Power and Energy Conversion Systems (EPECS 2013), Istanbul, 2-4 October 2013, 1-6. http://dx.doi.org/10.1109/EPECS.2013.6713054










