Smart Grid and Renewable Energy
Vol.2 No.1(2011), Article ID:4035,6 pages DOI:10.4236/sgre.2011.21003
Temperature and Heat Flux Distributions through Single and Double Window Glazing Nongray Calculation
![]()
1Civil and Architectural Engineering Department, College of Engineering, Sultan Qaboos University, Al-Khoud, Sultanate of Oman; 2Institute of Fluid Science, Tohoku University, Katahira, Japan.
Email: mkhoukhi@squ.edu.om
Received December 19th, 2010; revised December 29th, 2010; accepted January 5th, 2011.
Keywords: Glass Window, Nongray Calculation, Radiative Heat Transfer, Temperature Distribution, Heat Flux, Heat Generation
ABSTRACT
Accurate prediction of thermal radiation by applying rigorous model for the radiative heat transfer combined with the conduction and the convection has been performed for a single and double window glazing subjected to solar and thermal irradiation. The glass window is analysed as a non-gray plane-parallel medium disctritized to thin layer assuming the glass material as participating media in one-dimensional case, using the Radiation Element Method by Ray Emission Model (REM2). The model allows the calculation of the steady-state heat flux and the temperature distribution within the glass cover. The spectral dependence of the relevant radiation properties of glass (i.e. specular reflectivity, refraction angle and absorption coefficient) is taken into account. Both solar and thermal incident irradiations are applied at the boundary surfaces using the spectral solar model proposed by Bird and Riordan. The optical constant of a commercial clear glass material have been used. The calculation has been performed during winter period and the effect of the thickness of the glass for a single glazing and of the air layer between the two panels for double glazing has been studied. The result shows that increasing the air layer, the steady heat flux decreases and the temperature distribution within the glass changes.
1. Introduction
The accurate prediction of the temperature distribution through a glazing system depends strongly on how the glass material is analyzed. In general the glass material is assumed to be transparent for the solar spectrum and opaque to radiation at infrared wavelengths. Therefore, the gray approach is often assumed for such calculation. These assumptions may lead to considerable error in evaluating the thermal properties, heat flux and temperature distribution within the glass material subjected to irradiation. In reality, the transmittance, like reflectance and absorbance, is a function of wavelength, angle of incidence of the incoming radiation, the real part n and the imaginary part k of the complex refractive index of the glasscover [1,2]. Moreover, the real and imaginary parts of the complex refractive index of glass are spectrally dependent.
In the present work, the glass window is considered to be a participating non-gray media subjected to solar irradiation (specified by the spectral solar model proposed by Bird and Riordan, [3]) and thermal radiation (specified by blackbody emission of the outside and inside environment). A more refined and rigorous approach is applied using the Radiation Element Method by Ray Emission Model (REM2). The REM2 is a generalized method for calculating radiation heat transfer between absorbing, emitting and scattering media. The boundary surfaces of the glass are specular and the spectral dependence of radiation properties such as specular reflectivity, refraction angle and absorption coefficient are all taken into consideration.
The REM2 method was proposed by Maruyama and Aihara [4] and can be applied for complicated three-dimensional shapes. Numerous researchers have studied heat transfer by combined conduction and radiation in glass medium. Khoukhi et al. [5,6] have analysed the combined non-gray radiative and conductive heat transfer in solar collector glass cover using different model with regard to the optical constant of the glass material. Kong and Viskanta [7] have compared the diffusion approximation and Discrete Ordinate Method (DOM) for determining heat transfer in glass. The effect of the refractive index on radiative behaviour of heated absorbing-emitting layer has been reported by Spuckler and Siegel [8]. The combined conduction and radiation in two-layer planar medium with flux boundary conditions has been studied by Ho and Ozisik [9].
In this paper, the single and the double glazing models were considered and the effect of the thickness of the glass for single panel, and the vacuum layer between the two panels for the double glazing, on the temperature and heat flux distribution were investigated. The optical constant of a commercial clear glass material have been used [6]. Using this data, the calculation has been performed for one position of the sun during the winter period.
2. Analysis Model and Analytical Condition
Accurately speaking, the glass material is transparent to the solar radiation, due to the small value of k and it is strongly absorbing in the infrared region. Therefore, the emission and absorption within the glass layer should be taken into account.
2.1. Analysis Model
Figure 1 and Figure 2 show the model of single glazing and double glazing subjected to collimated and diffuse solar and thermal irradiations. It is assumed that the glazing exists between two blackbodies which comprise the ambiences of the outside and inside. The analysis is carried out by dividing the glazing into a number of layers. Since the long-wavelength radiation from the ambient is mostly absorbed in the vicinity of the glass surface, the thickness of the element is thin (1 μm) at the glass surface and thick (200 μm) in the middle of the glass sheet. The total number of element is set at 103 and 229 for the single and double glazing, respectively. The double glazing is constituted by two single glasses and we assume that between the two glasses a vacuum space exists. Therefore, the absorption and the convection are negligible in the vacuum space. The space between two glasses has been descritized into thin layers and the conduction is taken into account. Tin, Tout and θo are the inside temperature, the outside temperature and the incident angle of collimated solar irradiation, respectively.
For the calculation presented here, it is assumed that the thickness of a single glass panel is 3 mm. The convection is taken into consideration as boundary conditions in both sides of the glass with hin and hout are the inside and outside convective heat transfer coefficient,

Figure 1. Analysis model of single glazing.
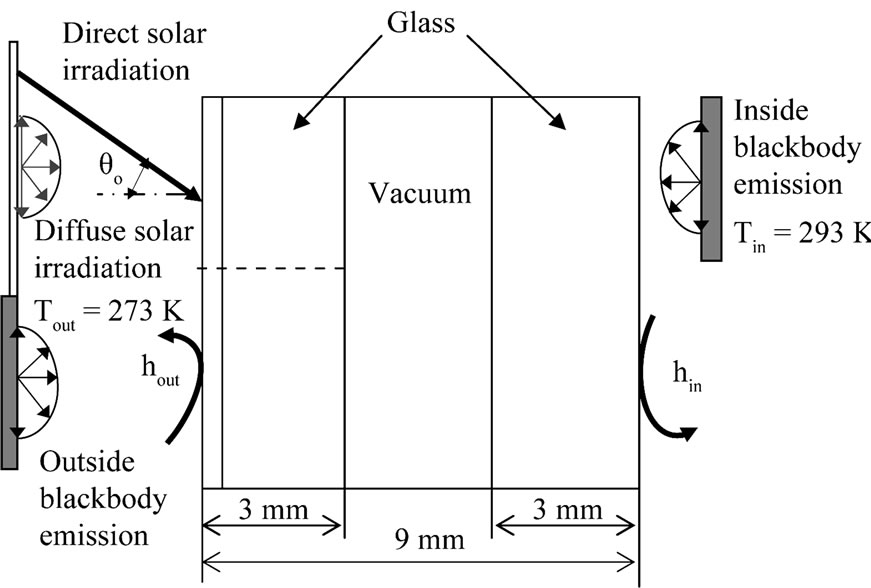
Figure 2. Analysis model of double glazing.
respectively and the thermal conductivity of the glass material is assumed to be constant.
The glass window is completely transparent for the direct solar irradiation (no absorption). On the other hand, the diffuse solar irradiation and the thermal infrared radiation from the outside and the thermal infrared radiation from the inside are absorbed and emitted within the glass-cover material (see Figure 3).
2.2. Analytical Assumptions
In the present study, the following assumptions are applied for the analysis. a) Since the thickness of the glass panel is much larger than the wavelength of the radiation, the coherence effects are neglected. b) The glass surfaces are optically smooth, and the incident radiation is specularly reflected. c) The scattering in the glass medium is neglected. d) The thermal conductivity of the glass material is assumed to be constant and independent of its temperature. e) The directional reflectivity has been computed from Fresnel equation as function of the complex re-
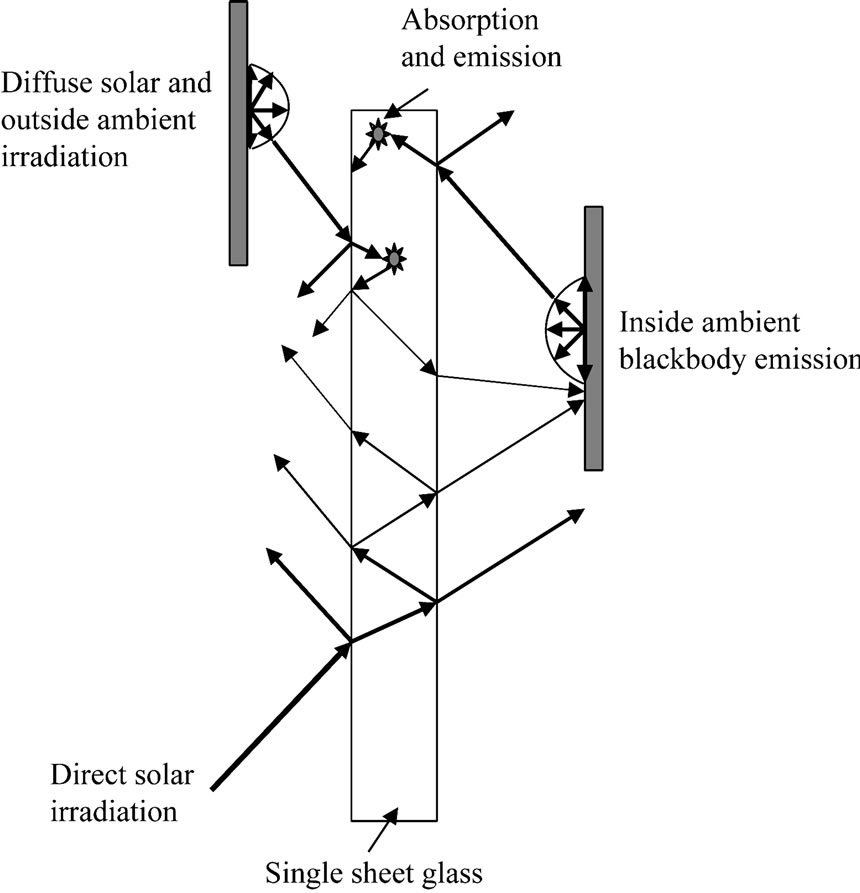
Figure 3. Real behaviour of glass window subjected to direct and thermal radiations.
fractive index of the glass and the incident angle.
2.3. Analytical Conditions
The numerical simulation has been carried out for one location on January 1, in Sendai city (Japan). Table 1 shows the site characteristics and other parameters used in numerical simulation. The initial glass temperature, the outside and inside ambient temperatures are 290 K, 273 K and 293 K, respectively. Since the variation of the physical properties of the air and the glass material as a function of the temperature is small, it is assumed that their values are constants for a given initial values. The thermal conductivity, the density and the specific heat of the glass and air are given by Table 2.
2.4. Spectral Distribution of Incident Radiation
2.4.1. Solar Irradiation Model
For solar irradiation, the spectral solar model proposed by Bird and Riordan [3] is used. With this model, the direct normal spectral irradiance from solar incident on the ground surface is given as
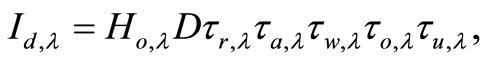 (1)
(1)
where Ho,λ is the extraterrestrial irradiance at the mean earth-sun distance for wavelength λ, D is the correction
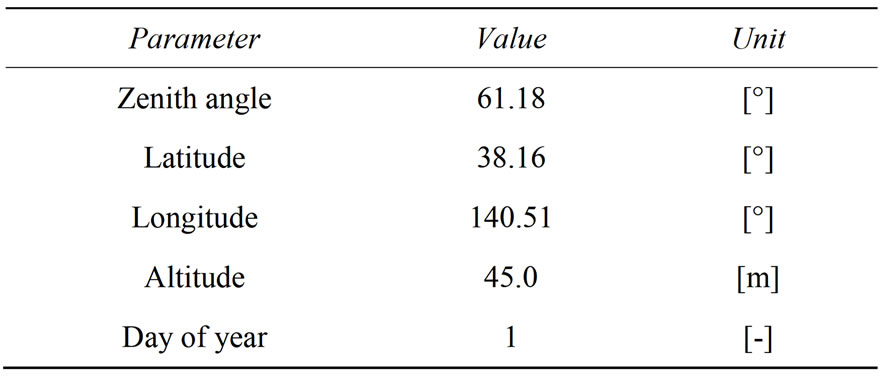
Table 1. Characteristics of the site and other parameters used in numerical simulation (Sendai, Japan).
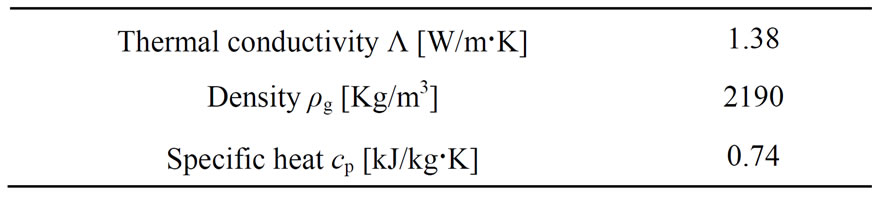
Table 2. Thermophysical properties of glass.
factor for earth-sun distance, and tr,λ, ta,λ, tw,λ, to,λ and tu,λ are transmittance functions of the atmosphere at wavelength λ for Rayleigh scattering, aerosol attenuation, water vapour absorption, ozone absorption, and uniformly mixed gas absorption, respectively.
The diffuse irradiance on the horizontal surface is divided into three components: 1) the Rayleigh scattering component Ir,λ, 2) the aerosol scattering component Ia,λ and 3) the component that accounts for multiple reflection of irradiance between the ground and air Ig,λ. The total scattering irradiance Is,λ is then given by the sum
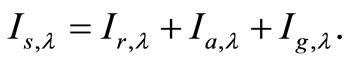 (2)
(2)
The spectral global irradiance on an inclined surface is represented by Equation (3) below. Where θ is the angle of incidence of the direct beam on the tilted surface and β is the tilt angle of the inclined surface. The first term in Equation (3) is the direct component on the inclined surface. The second and third terms account for the circumsolar or aureole component and the diffuse skylight component. The last term in Equation (3) represents the isotropically reflected radiation from the ground and given by
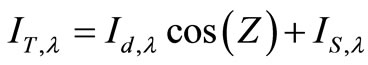 (4)
(4)
where Z is the solar zenith angle.
2.4.2. Spectral Distribution of Incident Radiation
The spectral distribution of the emissive blackbody exterior and interior ambient at 273 K and 293 K, respectively, are given by the following expression as a function of wavelength (λ) and blackbodies’ absolute temperature
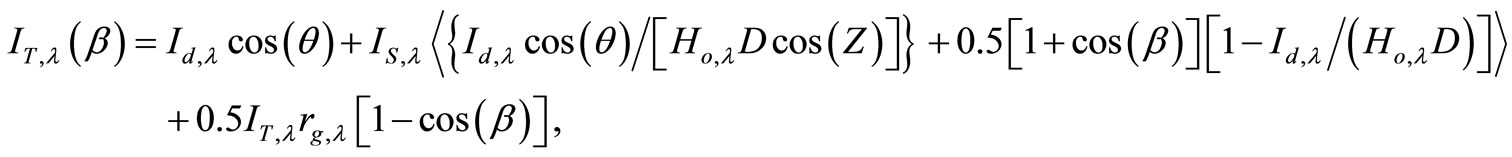 (3)
(3)
(T) (Plank’s Law)
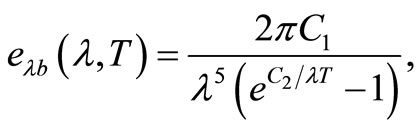 (5)
(5)
where C1 and C2 are the constant of Plank’s spectral intensity distribution and equal to 0.59552 × 108 W·μm4/ (m2·sr) and 14387.69 μm·K, respectively.
2.5. Radiative Transfer
For radiation elements i and j, the absorption view factor, 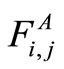 , is defined as a fraction of radiation energy emitted from element i and absorbed by element j.
, is defined as a fraction of radiation energy emitted from element i and absorbed by element j. 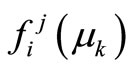 is the fraction of energy emitted from element i in the direction μk which reaches element j. The absorption view factor,
is the fraction of energy emitted from element i in the direction μk which reaches element j. The absorption view factor,  j, is given by
j, is given by
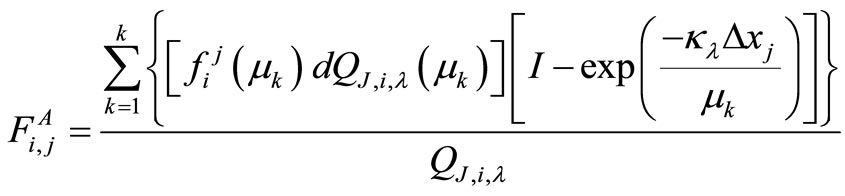 (6)
(6)
 Once the absorption view factor is given by using the ray tracing method, the net rate of heat generation in element i is given by
Once the absorption view factor is given by using the ray tracing method, the net rate of heat generation in element i is given by
 (7)
(7)
where QT,i,λ is the radiation energy emitted by element i itself and equal to QJ,i,λ. The heat transfer rate of the emissive power QT,i,λ or the net rate of heat generation QX,i,λ for each radiation element is given arbitrarily as a boundary condition. The unknown QX,i,λ and QT,i,λ can be obtained by solving equation (9) using the method described by Maruyama [4]. QJ,i,λ is eliminated from Equation (9) and the relation between QT,i and QX,i is obtained
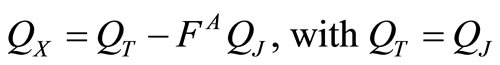 (8)
(8)
 (9)
(9)
The total net rate of heat generation is given by
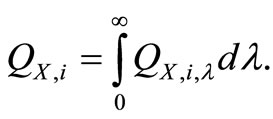 (10)
(10)
The heat generation rate per unit volume is
 (11)
(11)
Vi is the volume of the radiation element and Vi = Ai for a surface element.
Heat generation rate per unit volume by radiation means the divergence of radiative heat flux. Thereby, the radiative heat flux at position xn, is calculated as
 (12)
(12)
The radiation heat flux through the layer is derived as
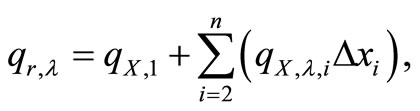 (13)
(13)
qX,1 includes the blackbody emission emanating from the ambient, and the diffuse and direct solar radiation components. In REM2, diffuse or collimated irradiation at the boundary surface can be treated [4].
2.6. Conduction and Convection Heat Transfer
The one-dimensional unsteady conductive heat transfer through the glass layer is given by
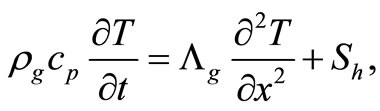 (14)
(14)
where ρg, cp, Λg, t and Sh are the density of the glass, specific heat of the glass, thermal conductivity of the glass, time and the heat generation source, respectively. The convection is taken into account as boundary conditions at both sides of the glass.
The outside and inside convective heat transfer h is determined by the following equations, assuming the natural convection of the air on the glass window
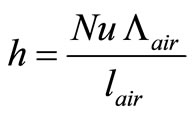 (15)
(15)
where Λair and lair are the thermal conductivity and the thickness of the air layer (= 1m), respectively. The Nusselt number, Nu, is given by the following relation
 (16)
(16)
The Raleigh number is given by
 (17)
(17)
The Grashof number is given as
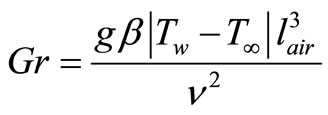 (18)
(18)
where g, υ and T∞ are the acceleration due to the gravity, kinematic viscosity of the air at the surface of the glass window and temperature of the air.
In the combined radiative and conductive heat transfer analysis, Equation (14) is discretized using the Finite Volume Method [10]. At first, for a given initial temperature distribution, the radiation heat generation rate per unit volume and the convective heat flux from ambient air are calculated. Then, these values are substituted as the source term Sh, or considered as the boundary condition of Equation (14). Next, the temperature distribution after some interval is obtained using the fully implicit method. The same calculation is carried out for the next temperature distribution until the steady-state condition is achieved.
3. Results and Discussion
The effect of the thickness on the heat flux passing through the glass-window is clearly shown in Figure 4. Increasing the thickness of the glass panel from 3 mm to 6 mm the heat flux through the window decreases slightly. This is essentially due to the increase of the absorption of the thermal radiation within the glass material and then this accumulated heat is reradiated into the inside space. Even though, the difference exists, the 3 mm thickness is more suitable with regard to the cost and the weight of the window compared with 6 mm thickness. The use of an antireflection coating on the outer surface of the glass panel would increase the heat transmitted through the glass during the winter period. Recently, a silica low-reflection coating via a dip-coating process has been developed, and the refractive index of the thin film is well controlled. Therefore, the exact value of the film refractive index that leads to a minimum of reflection on the outer surface of the glass can be achieved [11]. On the other hand, a special high-reflection coating on the inner surface of the glass would minimize the heat loss from the inside of the room to the outside.
Figure 5 shows the temperature distribution within the glass window material for both 3 mm and 6 mm thicknesses of the single panel. The gradient temperature between the ambient and the inside room is 20 K and the glass window is simulated during the cold period. Therefore, the effect of the conduction heat transfer within the glass is important compared with the radiation one. Consequently, the profiles of the temperatures distribution within a glass layers are linear in shape with the glass thermal conductivity constant. The temperature distributions within the single glasses are very close. However, the temperature of the inner surface of the glass with 6 mm thickness is slightly higher than the inner surface of the glass with 3 mm.
The steady heat flux through the double glazing windows with variable air space between the two panels is plotted in Figure 6. Indeed, the double glazing with 12 mm air gap thickness is more opaque rather than the other double glazing.
Figure 7 shows the temperature distribution with the double glazing with different air space thickness. This result shows that the inner surface temperature of the double glazing window with 12 mm air space thickness is higher than the inner surface temperatures of the other double glazing. This is due essentially to the thickness of the air space which plays a barrier again heat transfer. Moreover, comparing the heat transfer between the sin-

Figure 4. Heat flux through the single glazing.
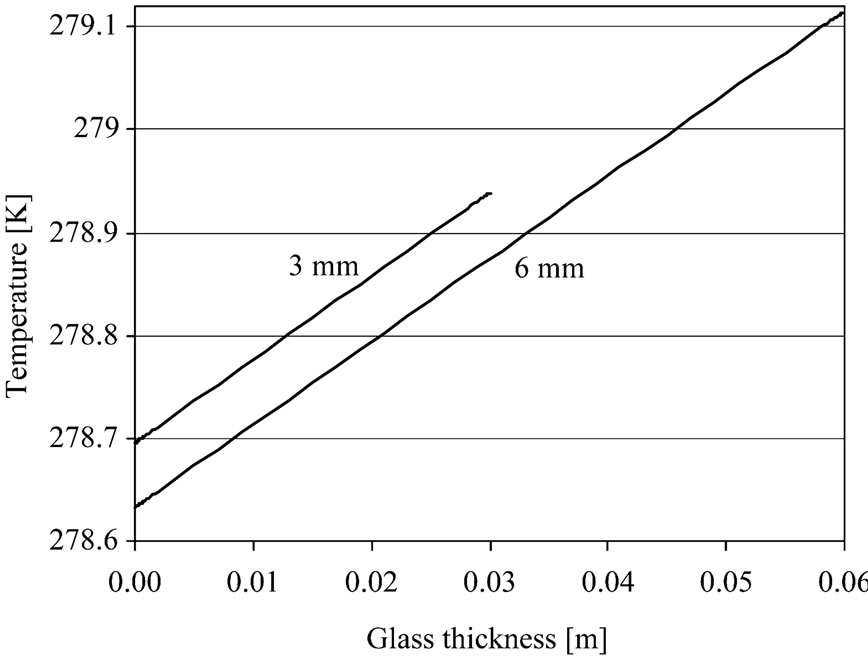
Figure 5. Temperature distribution within the single glazing window.
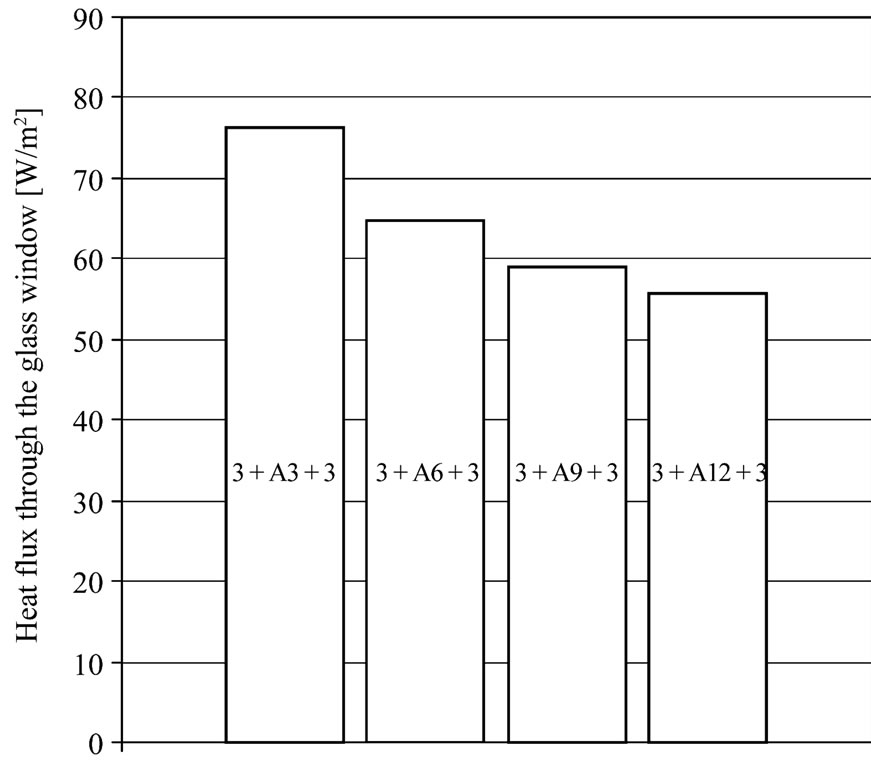
Figure 6. Heat flux through the double glazing.
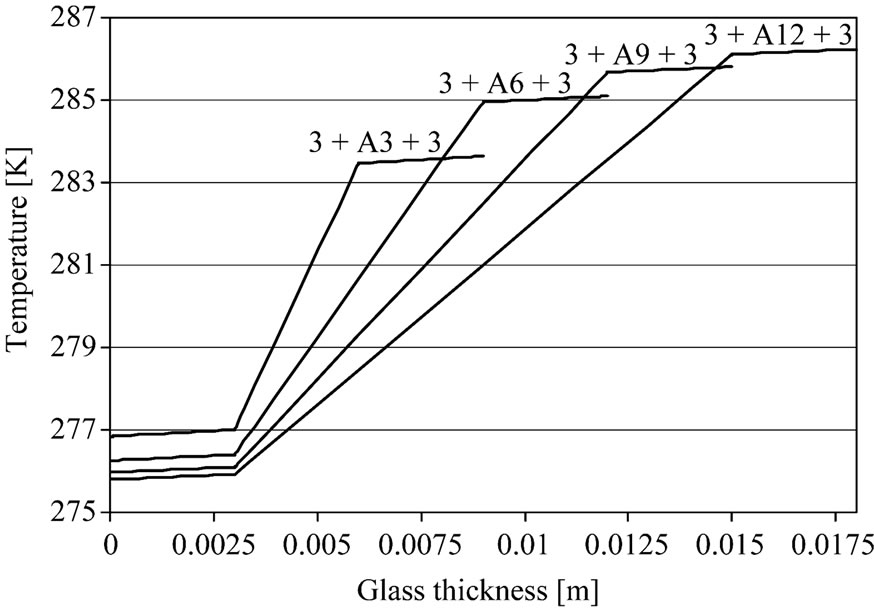
Figure 7. Temperature distribution within the single and double glazing window.
gle glazings with 3 mm thickness with the double glazing with 3 mm of air space thickness, less heat is lost from the inside to the ambient through the window when the double glazing is used. This result was expected, since the double glazing is more opaque for the radiation, and then prevents better the heat loss from the inside room to the outside surroundings.
4. Conclusion & Future Developments
Accurate modelling of a single and double glazing window system using rigorous radiative model has been presented. A non-gray computation procedure taking into account the absorption and emission within a glass layer is proposed. Steady-state heat flux and temperature distribution within the glass layer have been examined for a single and double glazing subjected to solar and thermal radiation during the winter period.
The thickness of the glass cover affects the heat flux through the glazing. In fact, increasing the thickness of the single glass window the heat loss from the inside to the outside decreases during the cold period.
It has been shown that the profiles of the temperatures distribution within a glass layers are linear in shape and the temperature distributions within the single glasses are very close. However, the temperature of the inner surface of the glass with 6 mm thickness is slightly higher than the inner surface of the glass with 3 mm.
The double glazing with 12 mm air gap thickness is more opaque rather than other double glazing, and the inner surface temperature of the double glazing window with 12 mm air space thickness is higher than the inner surface temperatures of the remaining double glazing.
As future work, the models developed for both single and double glazing will be simulated during the summer period. Moreover, to achieve energy conservation with the conditioned space, special coating on the surface of the glazing will be investigated using this rigorous approach.
REFERENCES
- J. R. Howell, B. B. Bannerot and G. C. Vliet, “SolarThermal Energy Systems Analysis and Design,” McGraw-Hill Inc., New York, 1982.
- J. A. Duffie and W. A. Beckman, “Solar Energy Thermal Process,” John Wiley & Sons, Inc., New York, 1974.
- R. E. Bird and C. Riordan, “Simple Solar Spectral Model for Direct and Diffuse Irradiance on Horizontal and Tilted Planes at the Earth’s Surface for Cloudless Atmospheres,” Journal of Climate and Applied Meteorology, Vol. 25, No. 1, 1986, pp. 87-97. doi:10.1175/1520-0450(1986)025<0087:SSSMFD>2.0.CO;2
- S. Maruyama and T. Aihara, “Radiation Heat Transfer of Arbitrary Three-Dimensional Absorbing, Emitting and Scattering Media and Specular and Diffuse Surfaces,” Journal of Heat Transfer, Vol. 119, No. 1, 1997, pp. 129-136. doi:10.1115/1.2824077
- M. Khoukhi, S. Maruyama, S. Sakai and M. Behnia, “Combined Non-Gray Radiative and Conductive Heat Transfer in Solar Collector Glass Cover,” Solar Energy, Vol. 75, No. 4, 2003, pp. 285-293. doi:10.1016/j.solener.2003.08.027
- M. Khoukhi, “Non-Gray Radiative and Conductive Heat Transfer in Single and Double Glazing Solar Collector Glass Cover,” International Journal of Thermal Sciences, Vol. 45, No. 6, 2006, pp. 579-585. doi:10.1016/j.ijthermalsci.2005.07.003
- H. L. Kong and R. Viskanta, “Comparison of the Diffusion Approximation and the Discrete Ordinates Method for the Investigation of Heat Transfer in Glass,” Glastechnische Berichte—Glass Science and Technology, Vol. 72, No. 8, 1999, pp. 254-265.
- C. M. Spuckler and R. Siegel, “Refractive Index Effects on Radiation Behaviour of Heated Absorbing-Emitting Layer,” Journal of Thermophysics and Heat Transfer, Vol. 6, No. 4, 1992, pp. 596-604. doi:10.2514/3.11539
- C. H. Ho and N. Ozisik, “Combined Conduction and Radiation in a Two-Layer Planar Medium with Flux Boundary Condition,” Numerical Heat Transfer, Vol. 11, No. 3, 1987, pp. 321-340. doi:10.1080/10407788708913557
- S. V. Patankar, “Numerical Heat Transfer and Fluid Flow,” Hemisphere Publishing Corporation, Washington DC, 1980, pp. 41-74.
- M. Khoukhi, S. Maruyama, A. Komiya and M. Behnia, “Flat-Plate Solar Collector Performance with Coated and Uncoated Cover,” Heat Transfer Engineering, Vol. 27, No. 1, 2006, pp. 46-53. doi:10.1080/01457630500343009

