Energy and Power Engineering
Vol.08 No.04(2016), Article ID:65582,9 pages
10.4236/epe.2016.84018
Harmonic Domain Modelling of Space Vector Based STATCOM
Devendra Manikrao Holey, Vinod Kumar Chandrakar
Department of Electrical Engineering, G. H. Raisoni College of Engineering, Nagpur, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 March 2016; accepted 15 April 2016; published 18 April 2016
ABSTRACT
This paper presents frequency domain method for harmonic analysis of space vector based STATCOM. Space Vector Pulse Width Modulation (SVPWM) method is an advanced PWM method. It is a best method among all the PWM techniques. It provides a freedom in a switching cycle for placement space vector. In this paper, the SVPWM is used for switching of STATCOM. The harmonic (or frequency) domain is a steady-state form of harmonic analysis method, which represents converters to their harmonic spectra. This paper presents harmonic analysis by means of harmonic domain for space vector based Static shunt converter (STATCOM). Performance of the STATCOM is evaluated in harmonic domain simulation studies in MATLAB environment.
Keywords:
Harmonic Domain, Voltage Source Converter (VSC), Space Vector Modulation (SVM), Static Shunt Compensator (STATCOM)

1. Introduction
Harmonic in power system is introduced by highly non-linear devices and it degrades its performance. Forced Commutated VSCs are the main building block for low and medium power application. Due to recent development in the semiconductor technology and availability of high power switches e.g. Insulated Gate Bipolar Transistor (IGBT) and Gate Turn off Thyristor (GTO) have widespread acceptance in for high power VSC’s, which are used for HVDC converters and FACTS controllers. The process of calculating the magnitude and phase of fundamental and higher order of system signals means power system harmonic analysis. The generation of harmonics in power system is due to large size of power converter. To reduce the harmonics in the system, filter and modern switching pattern are used. The increasing prevalence of flexible AC transmission system (FACTS) devices makes to have accurate model of these devices. One attracting method for modeling the steady state performance of these devices is frequency domain analysis [1] [2] . Harmonic phasor contains both positive and negative frequency terms for phase dependence. FACTS devices are characterized by their switching nature. For the reactive power compensation, the favorable FACTS device is STATCOM. STATCOM is a shunt connected device to regulate the voltage at the connected node [3] . To understand the interaction between the STATCOM based on VSC and utility system, there is a need of appropriate model.
VSC based STATCOM acts as source of harmonic current injection into the system and also interacts with harmonic distortions present within the system. To represent the harmonics interaction between STATCOM and system, as well as its effect on the system, it can be achieved from an accurate model of STATCOM based on VSC [4] . However, it is difficult to analyze the STATCOM, since it has both continuous and discrete time dynamics. Various switching techniques and modeling techniques are used for STATCOM to reduce effectively generated harmonics, including PWM techniques multi-module PWM techniques, selective harmonic elimination, and multi-level topology.
The Harmonic (frequency) Domain method is used for power system analysis in the steady state to model the coupling between phases and between harmonics. In Harmonic domain, the non-linear components such as converters are converted into Norton equivalents and then combined with the of the system admittance matrix and solved iteratively by the Newton-Raphson technique [2] [5] - [10] . The continuous time domain components of system are converted to the frequency domain and give much simpler representation of the components in the frequency domain than in the continuous time domain. The resulting waveform is decomposed into a finite set of harmonically related phasors, which add together to approximately recover the original waveform. Then, the system matrix equation is formed and the desired system quantities are obtained. The response of the network is determined from the individual phasors using the standard steady state network solutions. The total network solution is generated by superimposing the phasor solutions [7] .
Previous work conducted in harmonic domain has been primarily focus on modeling PWM, multi-module, selective harmonic elimination based STATCOM [11] . The complete equivalent circuit, represented as a harmonic Norton equivalent, is incorporated in the external system according to the transformer electrical connections [5] [12] - [15] .
A linear frequency domain model is given in [16] . Characteristics harmonics are derived from large signal transfer matrix and non-characteristics harmonics are calculated from small signal transfer matrix. Instantaneous power flow for harmonic calculation based on Newton Raphson method is given [17] [18] .
To extend the results obtained by other authors in the modeling of STATCOM FACTS device, the proposed SVPWM VSC based STATCOM model is developed in order to be able to obtain the evolution in harmonic components of the STATCOM signal. Harmonic analysis of PWM based STATCOM is shown in [1] . This paper presents the harmonic analysis of SVPWM based SSSC during steady state condition. The harmonic information can be used for control system design for space vector based STATCOM as space vector modulation scheme is more suitable for digital implementation. The paper is organized as follows. The second section provides fundamentals of harmonic domain method. Third section is fundamental of space vector based pulse width modulation based voltage source converter; this arrangement is used in this paper. Fourth section deals with harmonic domain modeling of SVPWM VSC used for STATCOM.
2. Analysis in the Harmonic Domain
Consider the non-linear relationship
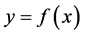 (1)
(1)
where x and y are periodic variables, which when determined by infinite Fourier series are expressed as follows
 (2)
(2)
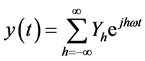 (3)
(3)
Let X and Y are the vectors of Xh and Yk Thus, Equation (1) takes the form
 (4)
(4)
If Equation (1) is differentiable, then for small increments about base values xy yb the following relationship is valid
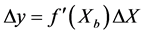 (5)
(5)
The linearised, general form of Equation (5) can be written as
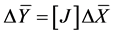 (6)
(6)
Matrix [J] of Equation (6) is the Jacobian associated with Equation (4).
Let us assume that the linearization process takes place about an operation point Xb Yb i.e.
 (7)
(7)
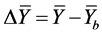 (8)
(8)
From Equations (6), (7) and (8)
 (9)
(9)
 is the Norton harmonic injection.
is the Norton harmonic injection.
From above equation, we conclude that every non-linear component should be amenable to a Norton equivalent representation in the Harmonic Domain [11] [19] .
3. Space Vector Modulation
3.1. Principles of SVPWM
Pulse Width Modulation (PWM) inverters play a major role in the field of power electronics [20] . Signal processing view point space vector modulation is a digital modulation technique. SVPWM is based in such a way that there are only two independent variables in a three-phase system. Orthogonal coordinates are used to represent the 3-phase voltage in the phasor diagram. A three-phase voltage vector represented by complex space vector as in Equation (1) neglecting zero sequence components [16] [18] [21] [22]
 (10)
(10)
SVM use the combinations of switching states to approximate the locus of Vref. In α-β plane, a hexagon centred at origin of αβ plane, identifies the space vectors shown in Figure 1. Space vector plane of Figure 1 is divided into six sectors. Each sector covers the space corresponding to 60˚.
The distinct possible switching states of the 2-level VSC are represented as eight voltage vectors, out of which six are active states (V1-V6) and two are null states (V0, V7). The active states contribute output line voltage as +Vdc or −Vdc, where as null states do not contribute any output voltage for VSC. The eight voltage vectors are shown in Table 1. ON state is denoted by 1of the switch and 0 denotes OFF state of the switch.
The reference vector is synthesized by the three adjacent switching vectors. For example, when Vref falls into sector I as shown in Figure 2, it can be synthesized by V1, V2 and V0. The volt second balance equation is
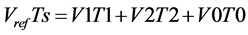 (11)
(11)
where Ts is the period of the switching cycle, T1 and T2 are the switching times of the vectors V1 and V2.
T1 and T2 are calculated as
 (12)
(12)
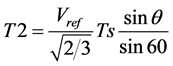 (13)
(13)
Figure 1. Switching vector of 2-level converter in αβ plane.
Figure 2. Representation of reference vector.
Table 1. 2-Level inverter voltage vectors voltage vectors.

Similar calculation is applied to sector II to VI Vector V8 can be used in place of V7. The choice is depend on the requirement to minimize average number of switching per cycle.
The Maximum value of Vref is obtain when θ = 30˚ and Vref is given by

This is the maximum value of line to line voltage injected by the converter. The maximum magnitude of Vref is also the radius of circle inscribed in the hexagon shown in Figure 1 The Square wave converter generates a space vector of magnitude 

3.2. Harmonic Domain Model of Switching Vector
The General switching function is obtained in time domain for space vector modulation. The harmonic content in switching function is given by Fourier series.



where Sa, Sb, Sc are switching function obtained by using SVPWM algorithm. The line switching vector is defined as

The switching vector for harmonic domain is defined as

4. STATCOM Based on PWM Converter
A STATCOM consist of VSI, DC capacitor and a coupling transformer. Figure 3 shows schematic re presentation STATCOM connected to an equivalent Ac power system where reactive power exchange between STATCOM and AC power system is take place. Inverter is made up of IGBT or GTO switches, which turn on and off at a rate considerably higher than power frequencies. SVPWM techniques are control the inverter output harmonics. Capacitor charges and discharges in every cycle. For steady state operation capacitor voltage is assume to be constant.
Harmonic Domain Model of STATCOM
Capacitor voltage of the STATCOM in the harmonic domain is given by [23]
Figure 3. STATCOM equivalent connected at PCC.

where Vcap is assembled with the harmonic content of Vcap(t) similarly Idc includes the harmonic contain of idc(t) and Edc contain a DC term, i.e.

Equation (3.1) can be written as

where 
The voltage on the DC side its relationship to the AC phase voltages are given in terms of switching function may be expressed in the harmonic domain as


The line current and the direct current relationship in harmonic domain is given by

Therefore, Thevenin equivalent of the three phase converter is given by

Thevenin impedance which is called as equivalent harmonic impedance as seen from AC side of converter is

And Thevenin equivalent voltage is given by Equation (14).

The Thevenin equivalent voltage is a constant three-phase harmonic voltage source which includes the effect of the SVPWM switching functions over the DC voltage. The Thevenin’s equivalent model of STATCOM is shown in Figure 4. Figure 4 also contains reactance of coupling transformer in series with ZTh.
5. Implementation of Equivalent Circuit of STATCOM
The Thevenin’s equivalent circuit of STATCOM incorporates the switching function. The switching function is obtained by using space vector modulation techniques. Space vector modulation was implemented in MATLAB code to obtain the Thevenin equivalent of the STATCOM. Figure 5 outlines this methodology.
Figure 4. Equivalent circuit of STATCOM.
5.1. Analysis of the Equivalent Circuit
Three phase circuit shown in Figure 3 was used to test the model with the constraint δ is =0. Since no active power exchange take place between STATCOM and system. System data is assumed as V = 1 p.u., R-0.0033 Ω, X = 0.1571 Ω, Re = 0.01 and Xe = 04712 Ω at 50 Hz. C = 1000 μF.
5.2. STATCOM Response
The DC voltage on the capacitor is assume to be 0.7 p.u. Then STATCOM absorb the reactive power. Figure 6 shows the voltages at the point of common coupling. Figure 6 shows that it contains harmonics. Harmonics in phase A at the inverter terminal is shown in Figure 7. Harmonics in phase A at the point of common coupling is shown in Figure 8 and Harmonics in the line current at the point of common coupling is shown in Figure 9.
6. Conclusions
This paper presents Space Vector based switching strategy for a STATCOM that utilizes the voltage source converter to minimize the harmonic at the point of common contact. The entire design of STATCOM and SVPWM is done in harmonic domain for calculation of harmonic interference in the system and evaluated based harmonic domain algorithms using MATLAB code.
The proposed model can be used to calculate harmonic interference produced by STATCOM. The simulation is fast and gives accurate result as compared to time domain simulation where we have to calculate first the
Figure 5. Flow chart outlining Thevenin equivalent.
Figure 6. Voltages at the inverter terminal.
Figure 7. Voltage harmonics in phase A at the inverter terminals.
Figure 8. Harmonics in phase A at the point of common coupling.
Figure 9. Harmonic in line current.
steady state condition then we can apply the Fourier analysis to calculate the harmonic in the system. The study result shows that when we use the Space vector modulation the power quality of the system is improved.
Cite this paper
Devendra Manikrao Holey,Vinod Kumar Chandrakar, (2016) Harmonic Domain Modelling of Space Vector Based STATCOM. Energy and Power Engineering,08,195-203. doi: 10.4236/epe.2016.84018
References
- 1. Collins, C.D., Bathurst, G.N., Watson, N.R. and Wood, A.R. (2005) Harmonic Domain Approach of STATCOM Modelling. IEE Proceeding Generation Transmission, Distribution, 152, 194-200.
http://dx.doi.org/10.1049/ip-gtd:20041227 - 2. Task Force on Harrnonics Modeling and Shulation (1996) Modeling and Simulation of the Propagation of Harmonics in Electric Power Networks Part II: Sample Systems and Examples. IEEE Transactions on Power Delivery, 11, 466-474.
http://dx.doi.org/10.1109/61.484131 - 3. Segundo-Rmirez, J. and Medina, A. (2001) Modelling of FACTS Devices Based on SPWM VSC. IEEE Transaction on Power Delivery, 24, 1815-1823.
http://dx.doi.org/10.1109/TPWRD.2009.2028799 - 4. Saeedifard, M., Nikkhajoci, H. and Iravani, R. (2007) A Space vector Modulated STATCOM Based on a Three-Level Neutral Point Clamped Converter. IEEE Transaction on Power Delivery, 22, 1029-1039.
http://dx.doi.org/10.1109/TPWRD.2007.893448 - 5. Amllaga, J., Medina, A., Lisboa, M.L.V., Cavia, M.A. and Sanchez, P. (1995) The Harmonic Domain. A Frame of Reference for Power System Harmonic Analysis. IEEE Transactions on Power Systems, 10, 433-440.
http://dx.doi.org/10.1109/59.373968 - 6. Task Force on Harrnonics Modeling and Shulation (1996) Modeling and Simulation of the Propagation of Harmonics in Electric Power Networks Part I: Concepts, Models, and Simulation Techniques. IEEE Transactions on Power Delivery, 11, 452-465.
http://dx.doi.org/10.1109/61.484130 - 7. Lian, K.L. and Lehn, P.W. (2006) Steady-State Solution of a Voltage-Source Converter with Full Closed-Loop Control. IEEE Transactions on Power Delivery, 21, 2071-2081.
http://dx.doi.org/10.1109/TPWRD.2006.877081 - 8. de Carvalho, N.B. and Pedro, J.C. (1998) Multitone Frequency-Domain Simulation of Nonlinear Circuits in Large- and Small-Signal Regimes. IEEE Transactions on Microwave Theory and Techniques, 46, 2016-2024.
http://dx.doi.org/10.1109/22.739276 - 9. Chen, B.-S. and Hsu, Y.-Y. (2007) An Analytical Approach to Harmonic Analysis and Controller Design of a STATCOM. IEEE Transactions on Power Delivery, 22, 423-432.
http://dx.doi.org/10.1109/TPWRD.2006.883016 - 10. Acha, E., Semlyen, A. and Rajakovit, N. (1990) A Harmonic Domain Computational Package for Nonlinear Problems and Its Application to Electric Arcs. IEEE Transactions on Power Delivery, 5, 1390-1396.
http://dx.doi.org/10.1109/61.57981 - 11. Lima, L.T.G., Semlyen, A. and Iravani, M.R. (2003) Harmonic Domain Periodic Steady State Modeling of Power Electronics Apparatus: SVC and TCSC. IEEE Transactions on Power Delivery, 18, 960-967.
http://dx.doi.org/10.1109/TPWRD.2003.813805 - 12. Medina, A. and Arrillaga, J. (1992) Generalised Modelling of Power Transformers in the Harmonic Domain. Transactions on Power Delivery, 7, 1458-1464.
http://dx.doi.org/10.1109/61.141865 - 13. Noda, T., Semlyen, A. and Iravani, R. (2004) Entirely Harmonic Domain Calculation of Multiphase Nonsinusoidal Steady State. IEEE Transactions on Power Delivery, 19, 1368-1377.
http://dx.doi.org/10.1109/TPWRD.2004.829944 - 14. Louie, K.W., Wilson, P., Rivas, R.A., Wang, A. and Buchanan, P. (2006) Discussion on Power System Harmonic Analysis in the Frequency Domain. 2006 IEEE PES Transmission and Distribution Conference and Exposition Latin America, Caracas, 15-18 August 2006, 1-6.
http://dx.doi.org/10.1109/tdcla.2006.311607 - 15. Srirattanawichaikul, W., Premrudeepreechacharn, S. and Kumsuwan, Y. (2014) Modified Unipolar Carrier-Based PWM Strategy for Three-Level Neutral-Point-Clamped Voltage Source Inverters. Journal of Electrical Engineering & Technology, 9, 489-500.
http://dx.doi.org/10.5370/JEET.2014.9.2.489 - 16. Wood, A.R. and Osauskas, C.M. (2004) A Linear Frequency-Domain Model of a STATCOM. IEEE Transactions on Power Delivery, 19, 1410-1418.
http://dx.doi.org/10.1109/TPWRD.2004.829953 - 17. Bathurst, G.N., Watson, N.R. and Arrillaga, J. (2000) Modeling of Bipolar HVdc Links in the Harmonic Domain. IEEE Transactions on Power Delivery, 15, 1034-1038.
http://dx.doi.org/10.1109/61.871371 - 18. Madrigal, M. and Acha, E. (2002) A New Harmonic Power Flow Method Based on the Instantaneous Power Balance. A New Harmonic Power Flow Method Based on the Instantaneous Power Balance, 2, 655-662.
http://dx.doi.org/10.1109/ichqp.2002.1221513 - 19. Louie, K.W., Wilson, P., Mazur, R., Kent, K., Dommel, H.W. and Marti, J.R. (2007) Power System Harmonic Analysis in the Frequency Domain. Canadian Conference on Electrical and Computer Engineering, Vancouver, 22-26 April 2007, 1421-1424.
http://dx.doi.org/10.1109/ccece.2007.357 - 20. Nisha, G.K., Member, I., Ushakumari, S. and Lakaparampil, Z.V. (2012) Harmonic Elimination of Space Vector Modulated Three Phase Inverter. Proceeding International Multi-Conferences of Engineers and Scientists, Hong Kong, 14-16 March 2012, 7 p.
- 21. Tripura, P., Babu, Y.S.K. and Tagore, Y.R. (2011) Space Vector Pulse Width Modulation Schemes for Two-Level Voltage Source Inverter. ACEEE International Journal on Control System and Instrumentation, 2, 34-38.
- 22. Nanda, B. (2014) Total Harmonic Distortion of Dodecagonal Space Vector Modulation. International Journal of Power Electronics and Drive System (IJPEDS), 4, 308-313.
http://dx.doi.org/10.11591/ijpeds.v3i4.4279 - 23. Acha, E. and Madrigal, M. (2001) Power System Harmonics—Computer Modeling and Analysis. Wiley, New York.











