Energy and Power Engineering
Vol.07 No.10(2015), Article ID:59880,13 pages
10.4236/epe.2015.710044
Novel Adaptive Neural Controller Design Based on HVDC Transmission System to Damp Low Frequency Oscillations and Sub Synchronous Resonance
Samad Goli, Ahad Goli, Naser Taheri
Zanjan Regional Electric Company (ZREC), Zanjan, Iran
Email: n.taheri.1362@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 August 2015; accepted 21 September 2015; published 24 September 2015
ABSTRACT
This paper presents the effect of the high voltage direct current (HVDC) transmission system based on voltage source converter (VSC) on the sub synchronous resonance (SSR) and low frequency oscillations (LFO) in power system. Also, a novel adaptive neural controller based on neural identifier is proposed for the HVDC which is capable of damping out LFO and sub synchronous oscillations (SSO). For comparison purposes, results of system based damping neural controller are compared with a lead-lag controller based on quantum particle swarm optimization (QPSO). It is shown that implementing adaptive damping controller not only improves the stability of power system but also can overcome drawbacks of conventional compensators with fixed parameters. In order to determine the most effective input of HVDC system to apply supplementary controller signal, analysis based on singular value decomposition is performed. To evaluate the performance of the proposed controller, transient simulations of detailed nonlinear system are considered.
Keywords:
Synchronous Resonance, Neural Network Damping Controller, Quantum Particle Swarm Optimization, HVDC Transmission Systems, Low Frequency Oscillations

1. Introduction
Series capacitors have extensively been used as a very effective means of increasing the power transfer capability of a transmission lines and improving transient and steady state stability limits of power systems [1] -[3] . These improvements are done by compensating reactance of the transmission lines. Besides of having remarkable profits for this kind of compensation for transmission line, the risk of sub synchronous resonance (SSR) could also be brought to the power system which could cause severe damages to the shaft of the generator unit [4] [5] . SSR is a condition of an electrical power system where electrical networks exchange energy with the mechanical system of the generator at frequencies less than the nominal frequency of the transmission line [6] . At this situation, the turbine-generator oscillates at a frequency corresponding to the torsional mode frequency. The torsional oscillations may raise and result in the failure of the turbine shaft.
Numerous papers have been published about damping the SSR phenomenon. Eigenvalue analysis [7] -[9] , frequency scanning method [10] -[12] , time domain simulation [13] and Using Flexible AC Transmission Systems (FACTSs) controllers such as the static synchronous compensator (STATCOM) [14] , the static synchronous series compensator (SSSC) [15] [16] , the unified power flow controller (UPFC) [17] , the thyristor controlled series capacitor (TCSC) [18] and high voltage direct current (HVDC) transmission systems [19] [20] have been applied to prevent the SSR in power systems.
HVDC systems interconnect large power systems and offer economic benefits. The usage of these systems includes for example non-synchronous interconnection, control of power flow, and modulation to increase stability limits. Adding a supplementary damping controller to the HVDC converters can improve the modal damping of the turbine-generator system and thus allows higher levels of compensation ratio of the power system [21] [22] .
In this paper, a power system including turbine-generator and VSC HVDC transmission system has been modeled as nonlinear state space equations. These equations have been linearized around operating point in order to analyze the small-signal stability, design damping phase compensator and measurement of oscillation mode controllability. It is well known that tuning a damping compensator for particular operating point cannot guarantee its appropriate performance in other points. Also, it may not capable to block oscillations that arise from critical disturbances like three-phase faults and may have unacceptable response in nonlinear power system model. More recently, adaptive neural networks (ANN) have been successfully applied to the identification and control of nonlinear systems because they have the advantages of high computation speed, generalization, and learning ability. ANNs techniques have been applied for power system damping controller design such as implementing PSS in a single-machine infinite bus system [23] -[25] and supplementary damping controller for FACTS devices [26] [27] .
As mentioned earlier, using of HVDC and FACTS supplementary damping controller has been studied by many researchers. However, designing an adaptive damping controller with ability to adapt itself with any work point of power system has not been studied. Furthermore, input-output signal selection to have most effect on oscillation mode has not been studied until now. So in this paper, a supplementary adaptive controller based on a neural network is proposed to damp power system LFOs and SSOs. Also, input-output coupling is performed via singular value decomposition (SVD) criteria to obtain best damping for power system. Proposed controller includes two individual parts: neural identifier and neural controller. The online training method is applied to training the controller through neural identifier and then the performance of supplementary neural controller, which can be tuned for overall operating points, is compared with phase compensator.
2. Power System Equipped by HVDC and Turbine-Generator System
In [28] [29] , it is shown that HVDC system can improve the stability of power system using a supplementary controller. Also, controllability of electromechanical mode based on system inputs is investigated using singular value decomposition. But, resistance of DC cable which is most important component of the DC transmission line has been neglected. So in this paper, single turbine-generator system equipped with a VSC HVDC system paralleled with compensated AC and full model of a DC transmission lines are considered as Figure 1.
The AC side of each converter is connected to the line through a coupling transformer. The first voltage source converter behaves as a rectifier. It regulates the DC link voltage and maintains the magnitude of the voltage at the connected terminal. The second voltage source converter acts as a controlled voltage source, which controls power flow in VSC HVDC feeder. The four input control signals to the VSC HVDC are 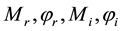 where
where 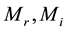 are the amplitude modulation ratio and
are the amplitude modulation ratio and 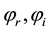 are phase angle of the control signals of each VSC respectively. The HVAC transmission line is represented by a reactance
are phase angle of the control signals of each VSC respectively. The HVAC transmission line is represented by a reactance 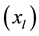 and a series fixed capacitive
and a series fixed capacitive
Figure 1. Turbine-generator system equipped by VSC HVDC and compensated lines.
compensation . The pure reactance of ac line can be considered as:
. The pure reactance of ac line can be considered as: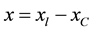 .
.
2.1. VSC HVDC Dynamical Model
By applying Park’s transformation and neglecting the resistance and transients of the coupling transformers, the VSC HVDC (Figure 1) can be modeled:
 (1)
(1)
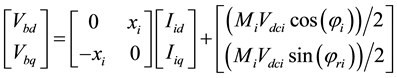 (2)
(2)
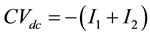 (3)
(3)
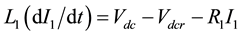 (4)
(4)
 (5)
(5)
where 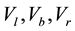 and
and 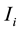 are the middle bus voltage, infinite bus voltage, flowed current to rectifier and inverter respectively. C and
are the middle bus voltage, infinite bus voltage, flowed current to rectifier and inverter respectively. C and  are the DC link capacitance and voltage, respectively.
are the DC link capacitance and voltage, respectively.  and
and 




where:





















where





And for inverter side:


By linearizing Equations (1)-(7), (13)-(16) (Detail of parameters are described in Appendix):




where:




2.2. Turbine-Generator Dynamic Model
The mechanical Turbine-Generator system corresponding to the electrical system (Figure 1) is shown in Figure 2 with detail. It consists of exciter (Ex.), generator (Gen.), intermediate pressure (IP), low-pressure (LP), high-pressure (HP) turbine sections. Every section has its own angular momentum constant M and damping coefficient D, also every two successive masses have their own shaft stiffness constant K. The equation of the ith mass of N-mass spring system shown in Figure 3 is given by:

3. Supplementary Damping Controller Design
The damping controllers are designed to produce an electrical torque in phase with the speed deviation to damp SSOs and LFOs. The four control parameters of the HVDC 
3.1. Lead-Lag Compensator based on QPSO
The structure of HVDC based damping controller is shown in Figure 4. It consists of gain, signal washout and phase compensator blocks. The signal washout is the high pass filter that prevents steady changes in the speed from modifying the VSC HVDC input parameter. The value of the washout time constant Tw should be high enough to allow signals associated with oscillations in rotor speed to pass unchanged. From the viewpoint of the
Figure 2. Turbine-generator system.
Figure 3. The ith mass of N-mass spring system.
Figure 4. Structure of lead-lag damping controller.
washout function, the value of Tw is not critical and may be in the range of 1s to 20 s. Tw equal to 10s is chosen in the present studies. The parameters of the damping controller are obtained using the particle swarm optimization technique [25] . In a PSO system [26] -[28] , multiple candidate solutions coexist and cooperate simultaneously. Each solution candidate, called a “particle”, flies in the problem space (similar to the search process for food of a bird swarm) looking for the optimal position. A particle with time adjusts its position to its own experience, while adjusting to the experience of neighboring particles. If a particle discovers a promising new solution, all the other particles will move closer to it, exploring the region more thoroughly in the process.
PSO starts [26] with a population of random solutions “particles” in a D-dimension space. The ith particle is represented by



where, pid = pbest and pgd = gbest.
PSO algorithm is as follow:
Step 1: Initialize an array of particles with random positions and their associated velocities to satisfy the inequality constraints.
Step 2: Check for the satisfaction of the equality constraints and modify the solution if required.
Step 3: Evaluate the fitness function of each particle.
Step 4: Compare the current value of the fitness function with the particles’ previous best value (pbest). If the current fitness value is less, then assign the current fitness value to pbest and assign the current coordinates (positions) to pbestx.
Step 5: Determine the current global minimum fitness value among the current positions.
Step 6: Compare the current global minimum with the previous global minimum (gbest). If the current global minimum is better than gbest, then assign the current global minimum to gbest and assign the current coordinates (positions) to gbestx.
Step 7: Change the velocities according to Equation (26).
Step 8: Move each particle to the new position according to Equation (27) and return to Step 2.
Step 9: Repeat Step 2 - 8 until a stopping criterion is satisfied or the maximum number of iterations is reached.
The main disadvantage is that the PSO algorithm is not guaranteed to be global convergent [28] . The dynamic behavior of the particle is widely divergent form that of that the particle in the PSO systems in that the exact values of xi and vi cannot be determined simultaneously. In quantum world, the term trajectory is meaningless, because xi and vi of a particle cannot be determined simultaneously according to uncertainty principle. Therefore, if individual particles in a PSO system have quantum behavior, the PSO algorithm is bound to work in a different fashion. In the quantum model of a PSO called here QPSO, the state of a particle is depicted by wave function W(x, t) instead of position and velocity [27] [28] . Employing the Monte Carlo method, the particles move according to the following iterative equation:


where u and k are values generated according to a uniform probability distribution in range [27] , the parameter 



The procedure for implementing the QPSO is given by the following steps [27] [28] :
Step 1: Initialization of swarm positions: Initialize a population (array) of particles with random positions in the n-dimensional problem space using a uniform probability distribution function.
Step 2: Evaluation of particle’s fitness: Evaluate the fitness value of each particle.
Step 3: Comparison to pbest (personal best): Compare each particle’s fitness with the particle’s pbest. If the current value is better than pbest, then set the pbest value equal to the current value and the pbest location equal to the current location in ndimensional space.
Step 4: Comparison to gbest (global best): Compare the fitness with the population’s overall previous best. If the current value is better than gbest, then reset gbest to the current particle’s array index and value.
Step 5: Updating of global point: Calculate the Mbest using Equation (30).
Step 6: Updating of particles’ position: Change the position of the particles according to Equation (29), where c1 and c2 are two random numbers generated using a uniform probability distribution in the range [0, 1].
Step 7: Repeating the evolutionary cycle: Loop to step 2 until a stop criterion is met, usually a sufficiently good.
3.2. Adaptive Neural Controller
In this section, a brief background on neural networks (NN) will be included covering mainly the topics that will be important in a discussion of NN applications in closed-loop control of discrete-time dynamical systems. Included are the NN topologies and recall, properties, training techniques, and control architectures. In this paper adaptive neural controller which is proposed to use in VSC HVDC model is as shown in Figure 5. This adaptive neural controller is consisted from two separate neural networks as identifier and controller described in following.
Structure of neural identifier is shown in Figure 6. f is activation function that is hyperbolic tangent. It is trained using error back propagation method that described in detail in following.
Coast function is defined as:

Figure 5. Structure of the online damping neural controller.
Figure 6. Structure of the online neural identifier.



and:

where 

Using sensitive coefficient in output neuron, it is possible to correct other weights between hidden and input layer.
Structure of neural identifier is shown in Figure 7. This is a feed forward network. Back propagation method used to train this network as described in following.
Coast function to training this network is:

and

v, 
Figure 7. Structure of the online neural controller.






Using Equations (36)-(38), it is possible to calculate the sensitive coefficient in output neuron of neural controller and correct the middle and output weights of neural controller.
4. Controllability of Oscillation Mode
The minimum singular value of the plant, 



respectively, such that: 












5. Simulation Results
SVD is employed to measure the controllability of the oscillation mode based on SSOs and LFOs from each of the four inputs:



・ EM mode controllability via 

・ The capabilities of 



・ The EM mode is controllable with 

Responses of linear and nonlinear system for some masses are shown in Figure 9. Obviously system is unstable. To assess the effectiveness of the proposed stabilizers following conditions are considered for linear and nonlinear system (Table 1).
Lead-lag controller based on QPSO is designed based on following objective function:
where, 
Figure 9 shows the load angle of mass-A in linear and nonlinear system. Obviously both systems are unstable.
Figure 10 and Figure 11 show the linear and nonlinear power system responses respectively. According to these figures, neural network damps active power and rotor speed oscillations better than lead-lag based on QPSO controller for disturbances. It is clearly seen that the dynamical performance at different loading conditions for a neural controller has more quality because neural controller decrease setting time and peak amplitude. Figure 10 shows the lead-lag based QPSO compensator cannot stabilize nonlinear system. In these figures, a three phase
Table 1. System condition.
Table 2. Neural controller characteristics.

Figure 8. Controllability measure using singular value decomposition for oscillation mode. (a) Qe = −0.3; (b) Qe = 0; (c) Qe = +0.3.

Figure 9. Response of some masses in turbin-generator system without installing any damping controller. (a) Linear system; (b) Nonlinear system.



Figure 10. Linear System Response for (a) Speed deviation for mass A; (b) Speed deviation for mass B; (c) Speed deviation for mass E; (d) Speed deviation for mass G; (e) Speed deviation for mass H; (f) Speed deviation for mass I; (g) Deviation of generated active power; (h) Deviation of modulation angle in rectifier; (i) Deviation of modulation index in rectifier.





Figure 11. Response of nonlinear system to a short circuit in infinite bus. (a) Deviation for modulation angle in rectifier side of HVDC (Δφr); (b) Generator terminal voltage; (c) Active power (produced by generator); (d) Load angle for mass A (δA); (e) Load angle for mass B (δB); (f) Load angle for mass E (δE); (g) Load angle for mass G (δg); (h) Load angle for mass H (δH); (i) Load angle for mass I (δI); (j) Shaft speed deviation for mass A (ωA); (k) Shaft speed deviation for mass B (ωB); (l) Shaft speed deviation for mass E (ωE); (m) Shaft speed deviation for mass g (ωg); (n) Shaft speed deviation for mass H (ωH); (o) Shaft speed deviation for mass I (ωI).
fault at t = 5 s accures and clears after 5 cycles. It is considered that phase compensator cannot damp oscillations for large disturbance. However neural controller has good responses in all operating conditions. As a result, neural controller improves dynamical and transient stability effectively.
6. Conclusion
In this paper, a novel dynamic model of turbine-generator system based on SSR which is equipped by VSC HVDC transmission system, is considered and supplementary controller is designed for improve power system stability and SSROs and LFOs oscillation damping. SVD has been employed to evaluate the oscillation mode controllability to the four VSC HVDC inputs. Also, for improving the system stability and damping oscillations, a neural controller is proposed. The simulation results has been carried out by SIMULINK/MATLAB show that the designed neural controller for system has the perfectly effect on dynamic and transient improvement in comparison with phase compensator.
Cite this paper
SamadGoli,AhadGoli,NaserTaheri, (2015) Novel Adaptive Neural Controller Design Based on HVDC Transmission System to Damp Low Frequency Oscillations and Sub Synchronous Resonance. Energy and Power Engineering,07,451-464. doi: 10.4236/epe.2015.710044
References
- 1. IEEE SSR Working Group (1985) Terms, Definitions and Symbols for Subsynchronous Oscillations. IEEE Transactions on Power Apparatus and Systems, PAS-104, 1326-1334.
- 2. IEEE SSR Task Force (1997) First Benchmark Model for Computer Simulation of Subsynchronous Resonance. IEEE Transactions on Power Apparatus and Systems, PAS-96, 1562-1572.
- 3. Pahlavani, M. and Mohamadpour, H. (2011) Damping of Sub-Synchronous Resonance and Low-Frequency Power Oscillation in a Series-Compensated Transmission Line Using Gate-Controlled Series Capacitor. Electric Power Systems Research, 81, 308-317.
http://dx.doi.org/10.1016/j.epsr.2010.09.007 - 4. Xie, X.R., Dong, Y.P. and Han, Y.D. (2012) Online Estimation of Turbine–Generator Shaft Fatigue Loss-of-Life Caused by Subsynchronous Resonance. Electric Power Systems Research, 92, 171-179.
http://dx.doi.org/10.1016/j.epsr.2012.06.014 - 5. Zhu, X., Sun, H., Wen, J. and Chen, S. (2014) A Practical Method to Construct Network State Equations in Multi-Machine System SSR Study. Electric Power Systems Research, 107, 51-58.
http://dx.doi.org/10.1016/j.epsr.2013.09.014 - 6. Orman, M., Balcerek, P. and Orkisz, M. (2012) Effective method of Subsynchronous Resonance Detection and Its Limitations. Electrical Power and Energy Systems, 43, 915-920.
http://dx.doi.org/10.1016/j.ijepes.2012.06.024 - 7. Fouad, A.A. and Khu, K.T. (1978) Subsynchronous Resonance Zones in the IEEE Bench Mark Power System. IEEE Transactions on Power Apparatus and Systems, PAS-97, 754-762.
http://dx.doi.org/10.1109/TPAS.1978.354546 - 8. Yan, A. and Yu, Y. (1982) Multi-Mode Stabilization of Torsional Oscillations Using Output Feedback Excitation Control. IEEE Transactions on Power Apparatus and Systems, PAS-101, 1245-1253.
http://dx.doi.org/10.1109/TPAS.1982.317386 - 9. Iravani, M.R. and Edris, A.A. (2002) Eigen Analysis of Series Compensation Schemes Reducing the Potential of Subsynchronous Resonance. IEEE Transactions on Power Systems, 10 (2).
- 10. Framer, R.G., Katz, E. and Schwalb, A.L. (1977) Navajo Project on Subsynchronous Resonance Analysis and Solutions. IEEE Transactions on Power Apparatus and Systems, 96 (4).
- 11. Edris, A. (1990) Series Compensation Schemes Reducing the Potential of Resonance. IEEE Transactions on Power Apparatus and Systems, 5, 219-226.
- 12. Rana, R.D., Huff, S.W., Hayes, R.M., Fromholtz, E.N. and Schulz, R.P. (1991) AEP’s Kanawha River 345kV Series Capacitor Installations-Subsynchronous Resonance Studies and Torsional Measurements. Proceedings of the American Power Conference, 53, 300-305.
- 13. Zhu, W., Spee, R., Mohler, R.R., Alexander, G.G., Mittelstadt, W.A. and Maratuhulam, D. (1995) An EMTP Study of SSR Mitigation Using the Thyristor Controlled Series Capacitor. IEEE Transactions on Power Delivery, 10, 1479-1485.
http://dx.doi.org/10.1109/61.400932 - 14. Padiyar, K. and Prabhu, N. (2006) Design and Performance Evaluation of Subsynchronous Damping Controller with STATCOM. IEEE Transactions on Power Delivery, 21, 1398-1405.
http://dx.doi.org/10.1109/TPWRD.2005.861332 - 15. Bongiorno, M., Ängquist, L. and Lennart, J.S. (2008) A Novel Control Strategy for Subsynchronous Resonance Mitigation Using SSSC. IEEE Transactions on Power Delivery, 23, 1033-1041.
http://dx.doi.org/10.1109/TPWRD.2007.908751 - 16. Bongiorno, M., Svensson, J. and Ängquist, L. (2008) On Control of Static Synchronous Series Compensator for SSR Mitigation. IEEE Transactions on Power Electronics, 23, 735-743.
http://dx.doi.org/10.1109/TPEL.2007.915178 - 17. Bo, W. and Yan, Z. (2002) Damping Subsynchronous Oscillation Using UPFC—A FACTS Device. Proceedings of the International Conference on Power System Technology, Kunming, 13-17 October 2002, 2298-2301.
- 18. Pilotto, L.A.S., Bianco, A., Long, W.F. and Edris, A.A. (2003) Impact of TCSC Control Methodologies on Subsynchronous Oscillations. IEEE Transactions on Power Delivery, 18, 243-252.
http://dx.doi.org/10.1109/TPWRD.2002.803835 - 19. Hamouda, R.M., Iravani, M.R. and Hackam, R. (1989) Torsional Oscillations of Series Capacitor Compensated AC/DC System. IEEE Transactions on Power Systems, 4, 889-896.
http://dx.doi.org/10.1109/59.32576 - 20. Jiang, Q.Y., Cao, Y.J. and Cheng, S.J. (2005) A Genetic Approach to Design a HVDC Supplementary Subsynchronous Damping Controller. IEEE Transactions on Power Delivery, 20, 1059-1064.
- 21. Villablanca, M., Valle, J.D., Rojas, J., Abarca, J. and Rojas, W. (2000) A Modified Back-to-Back HVDC System for 36-Pulse Operation. IEEE Transactions on Power Delivery, 15, 641-645.
http://dx.doi.org/10.1109/61.852998 - 22. Jiang-Hafner, Y., Duchen, H., Linden, K., Hyttinen, M., de Toledo, P.F., Tulkiewicz, T., Skytt, A.-K. and Bjorklund, H. (2002) Improvement of Subsynchronous Torsional Damping Using VSC HVDC. Proceedings of the International Conference on Power System Technology, Kunming, 13-17 October 2002, 998-1003.
- 23. Nguyen, T.T. and Gianto, R. (2008) Neural Networks for Adaptive Control Coordination of PSSs and FACTS Devices in Multi Machine Power System. IET Generation, Transmission & Distribution, 2, 355-372.
http://dx.doi.org/10.1049/iet-gtd:20070125 - 24. Segal, R., Kothari, M.L. and Madnani, S. (2000) Radial Basis Function (RBF) Network Adaptive Power System Stabilizer. IEEE Transactions on Power Systems, 15, 722-727.
http://dx.doi.org/10.1109/59.867165 - 25. Chaturvedi, D.K., Malik, O.P. and Kalra, P.K. (2004) Generalised Neuron-Based Adaptive Power System Stabilizer. IEE Proceedings—Generation, Transmission and Distribution, 151, 213-218.
http://dx.doi.org/10.1049/ip-gtd:20040084 - 26. Shayeghi, H., Jalili, A. and Shayanfar, H.A. (2008) Multi-Stage Fuzzy Load Frequency Control Using PSO. Energy Conversion and Management, 49, 2570-2580.
http://dx.doi.org/10.1016/j.enconman.2008.05.015 - 27. Awami, A., Abdel-Magid, Y. and Abidi, M.A. (2007) Particle-Swarm-Based Approach of Power System Stability Enhancement with Unified Power Flow Controller. International Journal of Electrical Power & Energy Systems, 29, 251-259.
http://dx.doi.org/10.1016/j.ijepes.2006.07.006 - 28. Shayeghi, H., Shayanfar, H.A., Jalilzadeh, S. and Safari, A. (2010) Tuning of Damping Controller for UPFC Using Quantum Particle Swarm Optimizer. Energy Conversion and Management, 51, 2299-2306.
http://dx.doi.org/10.1016/j.enconman.2010.04.002 - 29. Hsu, Y.Y. and Luor, T.S. (1999) Damping of Power System Oscillations Using Adaptive Thyristor-Controlled Series Compensators Tuned by Artificial Neural Networks. IEE Proceedings—Generation, Transmission and Distribution, 146, 137-142.
http://dx.doi.org/10.1049/ip-gtd:19990069 - 30. Changaroon, B., Srivastava, S.C., Thukaram, D., et al. (1999) Neural Network Based Power System Damping Controller for SVC. IEE Proceedings—Generation, Transmission and Distribution, 146, 370-376.
- 31. Banaei, M.R. and Taheri, N. (2009) HVDC Based Damping Controllers for Power System Stability. Proceedings of the 31st International Telecommunications Energy Conference, Incheon, 18-22 October 2009, 1-6.
http://dx.doi.org/10.1109/intlec.2009.5351746 - 32. Taheri, N. and Banaei, M.R. (2010) A Supplementary Neural Controller for Novel Modeling of VSC HVDC to Enhance Dynamic Stability in a Power System. Proceedings of the 1st Power Electronic & Drive Systems & Technologies Conference (PEDSTC), Tehran, 17-18 February 2010, 7-13.
- 33. Skogestad, S. and Postlethwaite, I. (2007) Multivariable Feedback Control—Analysis and Design. John Wiley & Sons, Chichester.
Appendix
































































































