Energy and Power Engineering
Vol.06 No.14(2014), Article ID:52259,9 pages
10.4236/epe.2014.614046
Selection of Best Materials and Parametric Optimization of Solar Parabolic Collector Using Fuzzy Logic
Sri P. Mohana Reddy*, Pathi Venkataramaiah, Devuru Vishnu Vardhan Reddy
Department of Mechanical Engineering, SV University, Tirupati, India
Email: *mohanareddypichela@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2014; revised 6 October 2014; accepted 26 October 2014
ABSTRACT
This paper focused on selection of best materials for absorber tube and reflective surfaces of Solar Parabolic Collector (SPC) using fuzzy logic, after analysing the material data. The glass mirror and Aluminium absorber have been identified as best materials. These selected materials are replaced in existing experimental setup. An experimental design is prepared based on the considered pa- rabolic collector parameters: Absorptivity, Reflectivity and Period of Sun Incidence. During experiments, outlet temperature of water and discharge is recorded for each experimental run. These data are analyzed using fuzzy Logic integrated with the Taguchi method and optimal parameter combination has been found.
Keywords:
Materials, Fuzzy Logic, Taguchi Method

1. Introduction
Among the renewable sources of energy, solar energy offers a practical solution for the energy problem which is clouding the prospects of mankind. The use of fossil fuel causes global warming, air pollution and acid rain. One to this harnessing of non-conventional, renewable and environment-friendly energy resources are vital for steering the global energy supplies towards a sustainable path (Silio Salcines and Renedo Estebanez 2009) [1] . Solar thermal systems play an important role in providing non-polluting energy for domestic and industrial applications. Concentrating solar technologies (Kaplanis and Barakos 2002) [2] , such as the parabolic collector, compound parabolic collector and parabolic trough can operate at high temperatures and are used to supply industrial
process heat, off-grid electricity and bulk electrical power (Rai 2010) [3] . Sinha and Sharma (2008) [4] formulated an analytical model for the parabolic collector of solar thermal electric power system which was developed for high-temperature applications.
P. Venkataramaiah (2013) [5] , et al. presented the Simulation and optimisation studies on a solar parabolic collector, and focused on parametric optimisation of a Solar Parabolic Collector done Desirability Functional Analysis approach. Priyabrata (2013) [6] , et al. applied fuzzy logic for selection of hydro turbine blade materials. For selection of best materials, various techniques such as Analytical Hierarchical Process (AHP), Fuzzy AHP, etc. are used by many researchers.
Mohana Reddy, et al. (2012) [7] proposed a methodology to find best materials for a solar flat-plate collector using the AHP technique. Oguzhan Yilmaz et al. (2006) [8] introduced a user-friendly intelligent system for the selection of electro discharge machining (EDM) parameters using MATLAB Fuzzy Logic Toolbox.
Tzeng and Chen (2007) [9] described the application of the fuzzy logic analysis coupled with Taguchi method to optimise the precision and accuracy of the high-speed electrical discharge machining (EDM) process. Rajyalakshmi et al. (2012) [10] used fuzzy logic integrated with Taguchi method for optimization of process parameters of wire electrical discharging machine. Sarfaraz Khabbaz et al. (2009) [11] applied a simplified fyzzy logic approach for material selection in mechanical engineering design. Vimal Sam Singh, et al. (2009) [12] worked on modelling and analysis of thrust force and torque in drilling GFRP composites by multi-facet drill using fuzzy logic. Zadeh, L. (1965) [13] explained the fuzzy sets, information and control. Kao C.C. et al., (2008) [14] introduced Fuzzy Logic Control of Micro-hole Electrical Discharge Machining, Journal of Manufacturing Science and Engineering. Lin J. L. et al., (2005) [15] used grey-fuzzy logic for the optimization of the manufacturing process.
Literature review reveals that no researcher uses the fuzzy logic for material selection and parametric studies in the area of solar energy systems. In the present study, fuzzy logic is used for selection of materials and optimisation of process parameters of a solar parabolic collector
2. Selection of Material for SPC Using Fuzzy Logic
2.1. Different Types of Materials and Its Properties
The different types of materials for absorber tubes and reflective surfaces are considered in this work and shown in Table 1 and Table 2. These materials are chosen for component of SPC to meet all performance requirements, ensure a long working with minimal or no required maintenance, and be cost effective. The properties of materials: density, thermal conductivity, cost, coefficient of thermal expansion, temperature, Corrosion resistantence which are input to fuzzy logic.
Table 1. Material properties for reflecting surfaces.
Table 2. Material Properties for absorber tube.
2.2. Material Selection Using Fuzzy Logic
Fuzzy logic is proved as effective tool for inferring or deducing information from a given set of facts and the reasoning process is simple, compared to computationally precise systems. Fuzzy logic can select the parameters or also materials rationally for optimizing complex combinations of technical and other properties which is hard to achieve manually. Hence, fuzzy logic theory can be used to select the optimum material for a function or optimum process parameters from a preranked groups based on their relevant properties. With these advantages the fuzzy logic is applied in this paper.
The fuzzy logic control allows the existence of uncertainty in handling parameter values. Fuzzy logic system comprises a fuzzifier, membership functions, a fuzzy rule base, an inference engine, and defuzzifier. The fuzzifier uses membership functions to fuzzify input values of each performance characteristic are shown in Figure 1.
The inference engine performs fuzzy reasoning on fuzzy rules to generate a fuzzy value. Finally, the defuzzifier converts fuzzy predicted value into a response value. In the following, the concept of fuzzy reasoning is described based on the five input-one-output fuzzy logic units. The fuzzy rule base consists of a group of if-then control rules with the five inputs, x1, x2, x3, x4 and x5 and one output y, i.e.
In the case of a material selection the total number of rules is equal to the number of fuzzy sets raised to the number of material properties being considered. Performance indices are calculated based on the material attri- butes. The indices are used to rank the performance of candidate materials from best to worst. In this paper the material properties such as density, thermal conductivity, coefficient of thermal expansion, corrosion resistant and cost are given as the input to fuzzy logic tool box to select best material for solar parabolic collector as shown in Figure 2.
Rule 1: if x1 is A1 and x2 is B1 and x3 is C1 and x4 is D1 and x5 is E1 then y is F1 else
Rule 2: if x1 is A2 and x2 is B2 and x3 is C2 and x4 is D2 and x5 is E2 then y is F2 else
……………………………………………………………………………………………
Rule n: if x1 is An and x2 is Bn and x3 is Cn and x4 is Dn and x5 is En then y is Fn else
Ai, Bi, Ci, Di and Ei are fuzzy subsets defined by the corresponding membership functions, i.e., μAi, μBi, μCi, μDi, μEi. In this section, three fuzzy subsets are assigned to the five inputs, as shown in Figure 2.
Figure 1. Fuzzy logic system.
Figure 2. FIS for material selection.
It is observed from Figure 3 that the fuzzy set for the density values between 5000 gm/cm3 and 15000 gm/ cm3 are as: below 5000 gm/cm3 is having excellent fuzzy set. Between 5000 - 15000 gm/cm3 it is having good fuzzy set.
From Figure 4, the fuzzy sets for the corrosion resistance values between PREN (pitting resistance equivalent number) values 32 and 78 are as: above 78 it is having excellent fuzzy set. Between 32 - 78 it is having good fuzzy set.
From Figure 5, the fuzzy sets for the thermal conductivity values between 0.25 and 0.75 are as: above 0.75 it is having excellent fuzzy set, between 0.25 - 0.75, it is having good fuzzy set.
From Figure 6, the fuzzy sets for the temperature values between 75˚C and 170˚C are as: above 170˚C it is having excellent fuzzy set, between 75˚C - 170˚C it is having good fuzzy set.
From Figure 7, the fuzzy sets for the cost values between 600 and 1500 are as: below 600 it is having excellent fuzzy set, between 600 - 1500 it is having good fuzzy set.
Five fuzzy subsets are assigned to the output, as shown in Figure 8. Forty three rules were developed based on their input values. By taking the max-min compositional operation, the fuzzy reasoning of these rules yields a fuzzy output that can be used to find the best material of SPC by giving rank to the response value.
2.3. Fuzzy Evaluation Results
This section presents the results of the material selection for solar parabolic collector. The results obtained from fuzzy logic are shown in Table 3 and Table 4. From these tables, the best materials Glass mirror for reflective
Figure 3. Membership function of density.
Figure 4. Membership function of corrosion.
Figure 5. Membership function of thermal conductivity.
Figure 6. Membership function of temperature.
Figure 7. Membership function of cost.
Figure 8. Membership function of output.
Table 3. Performance indices of reflective surfaces.
Table 4. Performance indices of absorber tube.
surface and Aluminium for absorber tube are selected based on their ranks.
3. Experimental Work
3.1. Description of Experimental Setup
Experimental setup consists of
• Parabolic Shaped Structure (made of MS Flat).
• Two legs to support the structure.
• Reflective Surface.
• Absorber tube.
• Auto Tracking System.
• Storage tank (Inlet & Outlet).
• Piping system (Figure 9).
Based on the reference [5] experimental setup has been prepared for conducting experiments, using the best materials obtained fuzzy logic. The entire set is placed in the N-S direction to face the axis of the parabolic trough towards east. The parabolic structure has a flexibility to change the reflective surface and Absorber tube materials. A provision has been made to change the position of absorber tube away from the focal point and also a mechanism is provided to change the angle of the absorber. A hydraulic actuator coupled with Light sensor is attached to the system for Auto-tracking. Light sensor senses the intensity of light and give signal to servo switch intern the signal is given to the hydraulic actuator.
3.2. Process Parameters and Their Levels
The process parameters considered in this work are: Absorptivity, Reflectivity and Period of Sun Incidence (POI). The Absorptivity is considered at three levels by coating with three coats; three Coating, are prepared by mixing silicon, black nickel and chromium with black enamel paint one at a time respectively and used for coating of best absorber tube which is selected through fuzzy logic. The reflective surface is considered at two levels, one is Glass mirror and other is silver mirror film. The process parameters and their levels are shown in Table 5.
3.3. Design of Experiment and Experimental Data
A Taguchi Experimental L18 design has been prepared based on the data of Table 5. Experiments are conducted according to the Taugchi design and the experimental results temperature and discharge are recorded as shown in Table 6.
Figure 9. Experimental setup of solar parabolic collector.
Table 5. Process parameters and their levels.
Table 6. Experimental results.
4. Determination of Optimum Process Parameters Using Fuzzy Logic
A fuzzy logic unit comprises a fuzzifier, membership functions, a fuzzy rule base, an inference engine, and a defuzzifier. First, the fuzzifier uses membership functions to fuzzify the S/N ratios. Next, the inference engine performs a fuzzy reasoning on fuzzy rules to generate a fuzzy value. Finally, the defuzzifier converts the fuzzy value into a MRPI. In the following, the concept of fuzzy reasoning is described briefly based on the two input-one-output fuzzy logic units. The fuzzy rule base consists of a group of if-then control rules with the two inputs, x1, x2 and one output y, i.e.
Rule 1: if x1 is A1 and x2 is B1 then y is C 1 else
Rule 2: if x1 is A2 and x2 is B2 then y is C 2 else
……………………………………………………
Rule n: if x1 is An and x2 is Bn then y is C n.
Ai, Bi and Ci are fuzzy subsets defined by the corresponding membership functions, i.e., μAi, μBi and μCi. In the present work, three fuzzy subsets are assigned to the two inputs, as shown in Figure 10 and Figure 11.
Five fuzzy subsets are assigned to the output, as shown in Figure 12. Nine fuzzy rules were developed based on the fact that a higher S/N ratio gives better performance. By taking the max-min compositional operation, the fuzzy reasoning of these rules yields a fuzzy output. Finally, a defuzzification method, called the centre of gravity method. Is adopted to transform the fuzzy inference output µD (Y1, Y2) into a non-fuzzy value Y0 [3] , which is known as the crisp output, that is calculated with the help
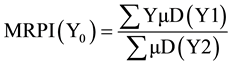
The non-fuzzy value Y0 gives MRPI. Invariably, a larger MRPI is preferred, which gives a better performance characteristic. Table 7 shows the results of the S/N ratios and MRPI for different experiment.
Figure 10. Membership function for S/N ratios of temp.
Figure 11. Membership function for S/N ratios of discharge.
Figure 12. Membership function for S/N ratios of MRPI.
4.1. Analysis and Discussion on Experimental Results Using MRPI
The experimental scheme used in this work is based on Taguchi’s orthogonal array, by which it is possible to separate the effect of each process parameter on the MRPI at different levels. The influence of each process parameter can be more clearly presented in means of the data mean response graph. The data mean graph shows the change in the response when a given factor goes from level 1 to level 3.
The optimum process parameters of the SPC are identified as shown in Figure 13 and Table 8. The absorptivity influences more and the Period of Sun Incidence has less influence on the responses.
Optimum parameters levels:
It is observed that the optimum combination of influential parameters is A2 B2 C2.
Which means:
A2: Reflectivity at level 2 (Glass Mirror) (0.97).
B2: Absorptivity at level 2 (U-tube Aluminium coated with Black Ni) (0.93).
C2: Period of Sun Incidence at level 2 (11.00 A.M - 1.00 P.M).
4.2. Confirmation Test
The optimum parameters obtained from fuzzy logic are Reflectivity (A2 at level 2 -0.97), Absorptivity (B2- 0.93), Period of Sun Incidence (C2-11.00 AM-1.00 PM) Ref section 4.1. An experiment is conducted for this combination of parameters for confirmation. The confirmation test (experiment) results are given in Table 9 and the conformation test result is satisfactory.
Table 7. S/N ratios and MRPI.
Figure 13. Main effects for data means.
Table 8. Optimum process parameters.
Table 9. Confirmation test results.
5. Conclusion
In this work, fuzzy logic is used for the material selection of Solar Parabolic Collector and for identification of process parameter by analyzing the data related to material properties such as price, thermal conductivity, density, temperature and corrosion. It is identified that Glass mirror and Aluminium tube are the best reflecting material and best absorbing material respectively. Finally, experimental response data are analyzed using fuzzy logic and optimum parameters levels have been identified. And these levels are confirmed experimentally.
References
- Silio Salcines, D. and Renedo Estebanez, C. (2009) Simulation of Solar Domestic Water Heating System, with Different Collector Efficiencies and Different Volume Storage Tanks. International Conference on Renewable Energies and Power Quality, 41, 111-120.
- Kaplanis, S. and Barakos, G. (2002) Flat Plate and Concentrating Collectors: A Comparison of Their Performances. Transilvania University of Brasov, Romania.
- Rai, G.D. (2010) Nonconventional Energy Recourses. Khanna Publishers, New Delhi.
- Sinha, U.K. and Sharma, S.P. (2008) Developed “Modelling for the Parabolic Collector for solar Thermal Electric Power”. ARISER, 4, 205-211.
- Venkataramaiah, P.P., Reddy, M. and Sairam, P. (2013) Simulation and Optimisation Studies on a Solar Parabolic Collector: An Experimental Investigation. Taylor & Francis group in International Journal of Sustainable Energy, 33. http://dx.doi.org/10.1080/14786451.778859
- Adhikary, P., Roy, P.K. and Mazumdar, A. (2013) Selection of Hydro-Turbine Blade Material: Application of Fuzzy Logic (MCDA). International Journal of Engineering Research and Applications, 3, 426-430.
- Mohana Reddy, P., Venkataramaiah, P. and Rohit, B.J. (2012) Selection of Materials for Solar Flat Plate Collector Using AHP. International Journal of Engineering Research and Applications, 2, 816-824.
- Yilmaz, O., Eyercioglu, O. and Gindy, N.N.Z. (2006) A User Friendly Fuzzy Based System for the Selection of Electro Discharge Machining Process Parameters. Journal of Materials Process Technology, 172, 363-371.
- Tzeng, Y. and Chen, F. (2007) Multi-Objective Optimization of High-Speed Electrical Discharge Machining Process Using a Taguchi Fuzzy-Based Approach. Journal of Materials and Design, 28, 1159-1168.
- Rajyalakshmi, G. and Ramaiah. P (2013) Optimization of Process Parameters of Wire Electrical Discharge Machining Using Fuzzy logic Integrated with Taguchi Method. International Journal of Scientific Engineering and Technology, 2, 600-606.
- Khabbaz, R.S., Manshadi, B.D., Abedian, A. and Mahmudi, R. (2009) A Simplified Fuzzy Logic Approach for Materials Selection in Mechanical Engineering Design. Materials and Design, 30, 687-697.
- Vimal Sam Singh, R., Latha, B. and Senthilkumar, V.S. (2009) Modelling and Analysis of Thrust Force and Torque in drilling GFRP Composites by Multi-Facet Drill Using Fuzzy Logic. International Journal of Recent Trends in Engineering, 1, 66-70.
- Zadeh, L. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Kao, C.C., Albert, J.S. and Miller, S.F. (2008) Fuzzy Logic Control of Micro-Hole Electrical Discharge Machining. Journal of Manufacturing Science and Engineering, 130, 064502-1.
- Lin, J.L. and Lin, C.L. (2005) The Use of Grey-Fuzzy Logic for the Optimization of the Manufacturing Process. Journal of Materials Processing Technology, 160, 9-14. http://dx.doi.org/10.1016/j.jmatprotec.2003.11.040
NOTES
*Corresponding author.
















