Energy and Power Engineering
Vol.06 No.05(2014), Article ID:46153,15 pages
10.4236/epe.2014.65010
CFD Prediction of the Turbulent Flow Generated in Stirred Square Tank by a Rushton Turbine
W. Chtourou, M. Ammar, Z. Driss, M. S. Abid
National School of Engineers of Sfax (ENIS), Department of Mechanical Engineering, Laboratory of Electromechanical Systems (LASEM), Sfax, Tunisia
Email: chtourouw@yahoo.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 February 2014; revised 13 March 2014; accepted 20 March 2014
ABSTRACT
The Computational Fluid Dynamics (CFD) have been used in the analysis and design of agitated vessel. Most of the researches done in this area are limited to the baffled or unbaffled stirred tank. In this paper, we have been interested in studying of the new design. Particularly, the flow and turbulence fields in square vessel stirred by a standard Rushton turbine have been simulated by means of CFD techniques. The Navier-Stokes equations governing the phenomenon of transfer of momentum are solved by a discretization method for finite volume. The MRF approaches can be used in simulation of the steady state problem. The numerical results from the application of CFD code Fluent with the stationary approach Multi Reference Frame (MRF) are presented in the planes containing the blade. The validation of CFD results with experimental measurements showed a good agreement.
Keywords:
CFD, Mixing, Turbulent, Rushton Turbine, Stirred Vessel

1. Introduction
Mixing is a very common operation in the process industries, usually performed by mechanical agitation.
Stirred tanks for the homogenization of single or several phases are among the most commonly used equip- ment in the chemical and biochemical processes. The accumulation of data on the operation of industrial agita- tors on the one hand, and a major research effort done in collaboration with academics, on the other hand, can provide experimental and theoretical support needed to technological advances. In view of the above, in the past, the impeller design and these characteristics have been the goal of most work. The flow generated by the Rush- ton turbines (RT) has been subjected to detailed experimental and computational studies. In the literature, sever- al works relating to the study of these types of turbines are already published. As a guide, one can cite the expe- rimental work conducted by Rushton [1] who studied the effect of a Rushton turbine on the evolution of the power number. These studies have shown that the design plays a key role in determining power consumption and agitator efficiency. It is worth noting that the tank design plays a key role in determining the power con- sumption and the agitator efficiency. Although this has become more routine for baffled vessels Montante et al., [2] [3] (2004, 2005) the unbaffled heavily swirling case is less well characterised by Armenante et al., [5] (1994), although a recent advanced LES study is noteworthy Alcamo et al., [6] . Even so, until very recently CFD only provided information on fluid mechanics, although just recently it is being exploited to predict mixing curves involving the evolution of concentration fields Yeoh et al. [7] , Montante et al. [3] . Yet, there are cases in which the use of unbaffled tanks may be desirable. First, baffles are usually omitted in the case of very viscous fluids (Re < 20), where they, giving rise to dead zones, would actually worsen the mixer performance, and where vortex formation is inhibited by the low rotational speed and by the high friction on the cylindrical wall Nagata [8] Unbaf- fled tanks are also advisable in crystallisers, where the presence of baffles may promote the particle attrition phe- nomenon Mazzarotta et al. [9] and Derkson, J. [4] . Finally, unbaffled tanks give rise to higher fluid-particle mass transfer rates for a given power consumption, which may be desirable in a number of processes Bakker et al. [10] .
Before this important flow of information in very little mechanical agitation is the work that has treated the influence of the square tank geometry. Among these works J. Kilander et al. [11] , studied experimentally the hydrodynamic parameters of turbulence in a square tank stirred with an axial impeller type A310 using the ap- proach (PIV) Large Eddy Particle Image Velocimetry. Suzanne M. Kresta et al. [12] conducted an experimental study of the batch mixture into a square tank stirred by using a spectrophotometer to a number of turbine type. This study shows that the correlation Grenville for determining the mixing time is checked for a square tank. J. Kilander et al. [13] determined the spatial and temporal evolution of the floc size distribution in a square 7.3 L tank stirred with an A310 hydro foil impeller investigated using PIV and image analysis. J. Kilander et al. [14] studied the size effect of the square tank on the mechanism of flocculation. The results show that there are large spatial differences in the mean size and the shape of the floc size distribution within the tanks but that the dif- ferences decrease as tank size increases from 5 to 28 l. However, increasing the size further to 560 increases the spatial variation.
View the lack of numerical results to evaluate and quantify the agitated vessel in square tank driven by a Rushton turbine, we are interested in this paper to the numerical simulation this type of system in fully turbulent regime.
2. Numerical Approach
2.1. Discretization Scheme
Some authors have investigated the effect of the discretization scheme on the accuracy of the predicted flow and in most cases have shown that the choice of discretization scheme has little or no effect on the solution. Bucato et al. [15] compared a hybrid scheme (upwind-central differencing) and the high-order QUICK scheme and found that predicted mean velocities did not differ appreciably. These authors concluded that for their model of 97,000 control volumes, numerical diffusion effects associated with the first-order upwind discretization scheme were not significant and that turbulent diffusion was largely dominant. However, no comparison of the effect of discretization on turbulence quantities was presented and it is not clear whether the results were grid indepen- dent. Aubin et al. [16] investigated three discretization methods (first-order upwind, upwind-central hybrid, QUICK) on a grid of 155,000 control volumes and found that the choice of the discretization scheme had no ef- fect on the mean velocities, except that the upwind scheme was found to under-predict the swirling region below the impeller. However, all three discretization schemes were found to under-predict the turbulent kinetic energy, this being most severe for the first-order upwind scheme in the impeller discharge stream.
2.2. Impeller Rotation Modelling
Modelling the impeller rotation is complex as the relative motion between the rotating impeller blades and the stationary tank wall causes a cyclic variation of the solution domain. Approaches to modelling the impeller rota- tion include using experimentally determined impeller boundary conditions, specifying momentum source/sink terms on the impeller blades or incorporating rotating and stationary reference frames. Two commonly used models are the Multiple Reference Frames and Sliding Mesh models. In these models, the solution domain is di- vided into an inner region containing the rotating impeller and an outer region containing the stationary tank wall. For the MRF model, steady-state calculations are performed with a rotating reference frame in the impeller region and a stationary reference frame in the outer region. In this way, the effects of the blade rotation are ac- counted for by virtue of the frame of reference, allowing for explicit modelling of the impeller geometry. For the SM model, the impeller region is allowed to slide relative to the outer region in discrete time steps and time- dependent calculations are performed using implicit or explicit interpolation of data at successive time-steps. Being time dependent, the SM method is the more accurate representation of the actual phenomenon of the im- peller rotation but is computationally demanding.
2.3. Reynolds Stress Modeling
There have been two attempts partially focused on the RSM for the flow generated by Rushton turbine in a baf- fled stirred vessel. First one, Bakker and Van den Akker [17] employed the simplified RSM, i.e. algebraic stress model (ASM) using the IBC method to model the flows produced by a Rushton turbine. Their objective was to improve the predictive capabilities of CFD modeling by accounting anisotropy using less computational inten- sive ASM model (simplified RSM). Their study concluded that the results predicted by the ASM compare better with the experimental data than those predicted by the standard k ? ε model. Oshinowo et al. [18] performed the CFD study using different turbulence models like, k ? ε, RNG k ? ε and RSM for the prediction of tangential velocity distribution in a baffled vessel using multiple reference frame (MRF) model. The tangential velocity distribution above the impeller has been correctly predicted. They attributed the occurrence of the counter-in- tuitive reverse swirl in the simulation to poor convergence and coarse grid density. It may be pointed out, how- ever, that both the aforesaid investigations have shown comparisons in only a small region while most of the vessel region remained unexplored. More importantly, both the studies have not presented the predictive capa- bility of CFD models for the turbulent kinetic energy and the turbulent energy dissipation rate.
3. Stirred Vessel Configuration
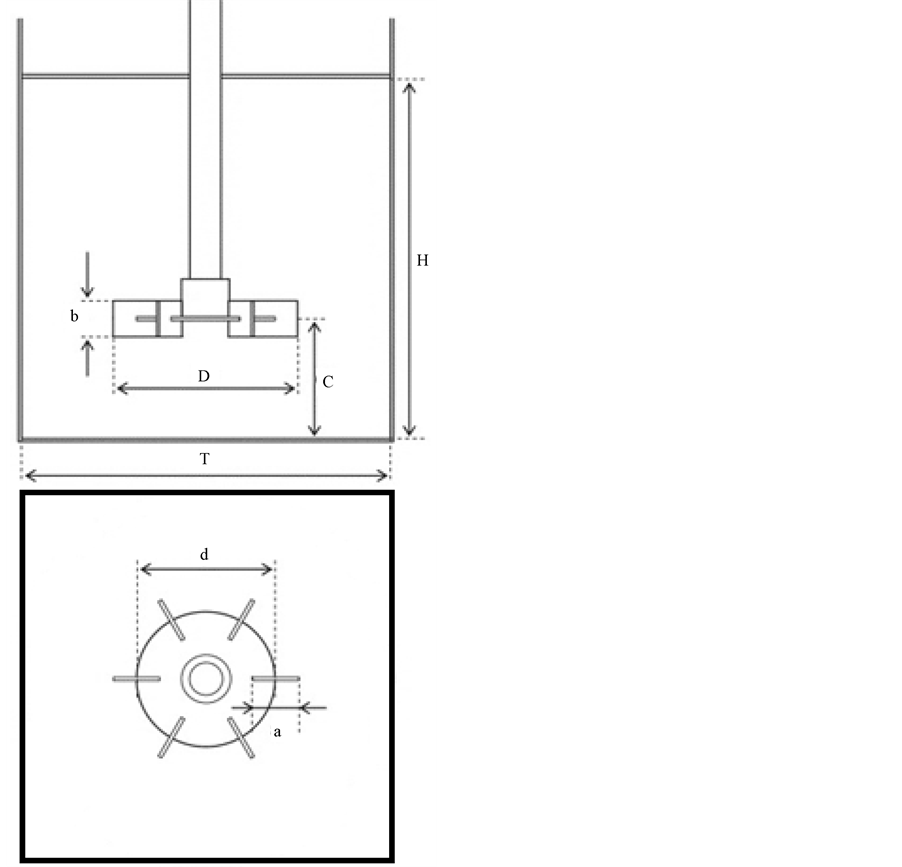
The tank geometry employed in this work is a square vessel depicted in Figure 1. The tank length T of 0.19 m
and was stirred by a Rushton turbine. The number of blade was six. The disk mounted impeller 0.095 m in di- ameter (D/T = 0.5), with standard proportions between parts (a = D/4, b = D/5, d = 3/4D. The impeller is installed along the axis of the tank with a shaft diameter of ds = 0.001 m and an off-bottom clearance of C = T/3. The vessel was 0.19 m tall (H = T) and was provided with a flat lid that inhibited the central vortex formation as well as any surface aeration. The tank was filled with pure water at room temperature. The rotational speed of the impeller N was 200 rpm (3.33 rps), resulting in a Reynolds number of about 4.2 × 104. In the numerical si- mulations, the fluid was assumed to be incompressible, isothermal and Newtonian with a density of 1000 kg∙m−3 and a dynamic viscosity of 1 × 10−3 Ns∙m−2.
4. Numerical Models
The CFD code Fluent with the multiple reference frames (MRF) was used for direct modeling of the impeller- tank interaction. Thus, no LDA data was used to obtain the CFD solution of the differential equations for mo- mentum transfer.
4.1. Boundary Conditions
The computational domain was split into two cylindrical zones. One of which is assumed to rotate with the im- peller angular velocity of ω = 2πN, while the remaining space can be modeled with a stationary reference. In that zone, the options of centrifugal and Coriolis forces were activated. The outer zone was stationary relative to the tank walls. Because the symmetry of the configuration, the half of the area will be analyzed. Figure 2 shows the subdivision of the computational domain with the MRF approach. For the closure of the above equations different turbulence models have been employed and these are described in the following section. The numerical solution of these equations was achieved by a finite-volume method (Burns & Wilkes, 1987), together with the Rhie and Chow (1983) algorithm to prevent “chequer-board” oscillations, both implemented in the computer
Figure 1. Vessel geometry.
Figure 2. Grid generation and computational domain.
code Fluent. Because there is no explicit equation for the pressure, special techniques have been devised to ex- tract it in an alternative manner. The most well known of these techniques is the SIMPLE algorithm, or Semi- Implicit Method for Pressure-Linked Equations, adopted by Patankar [19] to couple the continuity and Navier- Stokes equations. The hybrid-upwind discretisation scheme was used for the convective terms. The simulation was also performed using the standard differencing scheme in conjunction with the MRF method to test whether the use of a different scheme would have any impact on the solution. The computed flow field is identical to that obtained with the hybrid scheme and therefore the differencing scheme had no effect on the predictions. In all cases, conventional linear-logarithmic called wall functions were used on solid walls, while the free surface was treated as a symmetry plane. The solution convergence was carefully checked by monitoring the residuals of all variables as well as physical values of the swirl velocity. Residuals were dropped to the order of 10 - 5 or less, which is at least one order of magnitude tighter than Fluent’s default criteria.
4.2. Meshing
The grid elements can affect the quality of the solution. In fact, a preliminary grid convergence study was car- ried out in order to verify that the solution is a grid independent. For different types of meshes, we are interested to compare the numerical results with experimental data. The number of grid nodes in both zones, inner and outer mesh was systematically increased throughout the vessel. Generally, the numerical simulation with a coarse grid has a large deviation from the reference results. Gradually refining the grid, we note that the appear- ance of results stabilizes and approaches to the reference values. Also, it’s noted that it is unnecessary to further refine the mesh, because the calculation time becomes very large and the results found are almost the same. Thus, we show that there is a compromise between the mesh refinement and choice of computing time. In this work, we have used regular grid that containing hexahedral elements for the full domain simulation in order to conserve flux in each cell and to resolve the steep gradients in the impeller region. The total grid size of 115,000 was used for the full tank simulation. Impeller region (less than 5.5% of tank volume) was meshed with 15% of the total grid size used for the full tank in order to resolve the steep gradients in the impeller region. Similarly, near vessel wall were meshed with the dense grid. In this zone, corresponding to the fully-turbulent layer, the Y+ values is equal to 60.
4.3. Governing Equations
By all the computational approaches used in this work, the equations to be solved are the continuity and mo- mentum equations. The continuity equation is a statement of conservation of mass. For a constant density fluid, it takes the form:
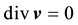 (1)
(1)
The momentum equations are a statement of conservation of momentum in each of the three components. The three momentum equations are collectively called the Navier-Stokes equations. In addition to momentum trans- port by convection and diffusion, several momentum sources are also involved. In cylindrical coordinates (r, θ, z), the momentum equations take the form:
 (2)
(2)
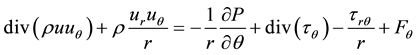 (3)
(3)
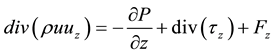 (4)
(4)
The total pressure P is defined by the following equation:
 (5)
(5)
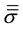 is the viscous stress tensor
is the viscous stress tensor
 (6)
(6)
Within:
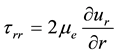 (7)
(7)
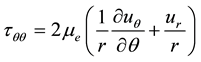 (8)
(8)
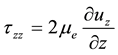 (9)
(9)
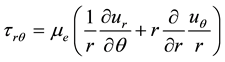 (10)
(10)
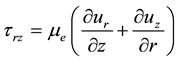 (11)
(11)
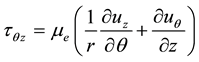 (12)
(12)
Fr, Fθ and Fz are respectively the centrifugal force, the Coriolis terms and the gravity. The expressions of these three terms are given in the following form:
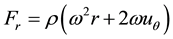 (13)
(13)
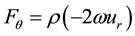
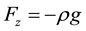
For the second-order model (RSM) used in this work, the turbulent kinetic energy and its dissipation rate are given by the system of equations as follows:
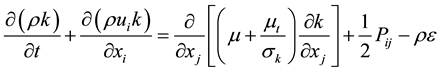

Due to gradients ways, the RSM model is characterized by the production term of the turbulent kinetic energy defined as follow:
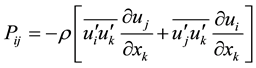
This module requires the use of empirical constants given in Table 1 as follows.
5. Results
5.1. Distribution of the Average Velocity in the Plane r-θ
Figure 3 shows the spatial distribution of mean velocity in three planes of the tank. These planes were located symmetrically above and below the plane containing the stirrer. In the central plane containing the turbine Fig- ure 3(b), the seat of the maximum average speed is localized in the area swept by the turbine and decreases be- tween the blade and at the turbine disk. In the area between the tips of turbine blades and the walls of the tank,
Table 1. Constant for the rms model.
Figure 3. Average velocity in the plane r-θ.
average speed is almost constant. At the walls of the tank, we note the zero values of average speed. In addition, the average speed is dropped in passing clockwise through the corner of the field. In conclusion, the square geometry of the tank destroys the tangential component of velocity and prevents the generation of vortices in the vicinity of the turbine. For the other two plans in Figure 3(a) and Figure 3(c) the spatial distribution of the av- erage velocity is very different than the previous plan. The area around the axis of the stirring spindle is charac- terized by a relatively constant average speed and exchanges in this field are purely convective. Near the walls of the tank we have a nonzero mean velocity. Hence the existence of a lateral flow parallel to the walls that fol- lows the formation of recirculation zones at the corners of the tank.
5.2. Distribution of the Average Velocity in the Plane r-z
In Figure 4, it is presented the spatial distribution of the average velocity in the plane containing the turbine blade TR6. View the geometry of the tank recovery plans are not the same size. From these results, we note the appearance of a wake maximum value that develops in the area swept by the turbine. The characteristics of radi- al jet turbine are kept for the three study designs: a large radial jet that develops at the end of the blade and an intense axial flow upward to the underside of the shaft that powers the turbine. View these dimensions and if the central plane Figure 4(a), the radial jet generates a low axial flow at the wall. Also note a recirculation loop that forms in the lower part of the plan. In the case of the plane of Figure 4(b), the spatial distribution of the average speed mark the disappearance of the recirculation loop in the lower part of the tank and the appearance of heavy traffic in the upper part. The radial jet created by the turbine generates an axial flow at the wall. The spatial dis- tribution of mean velocity in the plane of the Figure 4(c) ascended the presence of a plane that intensify the radial jet which reaches the lateral surface and is transformed into two axial jets up and down. The upward axial jet is more intense. It gives rise to a recirculation loop extended well into the upper area of the tank thereby feeding back the turbine.
In Figure 5 is presented the average velocity in the r-z plane located between two blades. Overall, the flow is less intense than in the planes containing the blades. The plan of Figure 5(a) is the plan as a lover of the central plane, where the spatial distribution of the average speed is more intense than that of the plane below the central plane Figure 5(b). Thus the passage of the flow through the central plane destroyed the tangential component of velocity and evidence of slowing the flow downstream of the corner of the square tank. As interpreted, the geo- metry of the vessel plays a very important role in the destruction of the tangential component of velocity and therefore prevents the formation of vortices around the impeller.
5.3. Distribution of Turbulent Kinetic Energy
Figure 6 presents the evolution of the distribution of the turbulent kinetic energy in the square vessel. The three
Figure 4. The average velocity in the plane r-z containing the blade.
Figure 5. Mean velocity in the plane r-z between blades.
planes in Figure 6 defined respectively by the axial coordinate equal to z = 1/2, z = 1/3 and z = 1/6. Maximum values are recorded in the plane containing the turbine at the axial coordinate z = 01/3. These values are located near the flat face of the square tank. The turbulent kinetic energy is very low in the corners of the tank at full plans. For the other two axial positions turbulent kinetic energy falling in a remarkable way. The minimum val- ues are located near the axis and corners of the square tank.
Figure 7 presents the turbulent kinetic energy in the plane containing the blades. The maximum values of
Figure 6. Turbulent kinetic energy in the plane r-θ.
Figure 7. Turbulent kinetic energy in the plane r-z containing the blade.
turbulent kinetic energy are noted in the plane containing the central blade q = 90˚. These values are located near the blade and diffused up the corner of the square tank. There are differences between the plane q = 30˚ and the plane q = 150˚: the thirst is the minimum values of turbulent kinetic energy are noted near the wall in the angu- lar position q = 150˚. The second concerned the spatial partition of the turbulent kinetic energy in the proximity of the Blade.
Figure 8 presented the turbulent kinetic energy in the planes located at the angular position q = 60˚ and q = 120˚. We note that, the tank design and the direction of the turbine rotation affected the partition of the turbulent kinetic energy. For these reasons, the partitions of the turbulent kinetic energy are more intense in the plane q = 120˚ and the maximum value are located in the proximity of the tank wall.
5.4. Distribution of Dissipation Rate of the Turbulent Kinetic Energy
In Figure 9, we presented the distribution spatial of the dissipation rate of the turbulent kinetic energy in planes located respectively at the axial coordinate equal to z = 0.4, z = 0.33 and z = 0.25. Globally, the geometry of the vessel affects the spatial distribution of dissipation rate of the turbulent kinetic energy. We note that the dissipa- tion of energy is in the plane containing the turbine. In this plan the energy is dissipated around the agitation blade and near the walls of the square tank. From both sides of this plan (z/H = 1/6, z/H = 1/2), the dissipation rate of turbulent kinetic energy was near the walls of the square tank.
Figure 10 present the evolution of the distribution of the dissipation rate of the turbulent kinetic energy in planes containing the blade. These results confirm that the dissipation rate of the turbulent kinetic energy was essentially in the region swept by the impeller turbine. We noted, that the maximum of the dissipation was form
Figure 8. Turbulent kinetic energy in the plane r-z between blades.
Figure 9. Distribution of dissipation rate of the turbulent kinetic energy in the plane r-q.
Figure 10. Distribution of dissipation rate of the turbulent kinetic energy in the plane r-z.
the angular position q = 90˚.
5.5. Distribution of Turbulent Viscosity
Figure 11 shows the evolution of the turbulent viscosity distribution in the same planes adopted in the previous paragraphs. We noted, the maximum value of the turbulent viscosity are located at the axial position z/H = 1/2. Globally, we find that the turbulent viscosity is very weak on the plane containing the impeller z/H = 1/3. In the symmetrical plane of this plane, it grows a wake characterized by relatively high values. At the proximity in the sidewall of the square tank, the turbulent viscosity drops rapidly.
Figure 12 show the spatial distribution of the turbulent viscosity in three planes containing the impeller blade. The turbulent viscosity has remained rather high in the field swept by blades of the turbine. Very near to the walls and around the turbine, the turbulent viscosity has made a very fast fall. By comparing the three planes between them, it has been noted that the maximal values of the turbulent viscosity in angular position q = 150˚. In general, the difference in the spatial distribution of turbulent viscosity in the plans shows the influence of tank geometry on the hydrodynamic structure.
5.6. Axial Profiles of the Velocity
5.6.1. Axial Profiles of the Velocity to an Angular Position q = 15˚
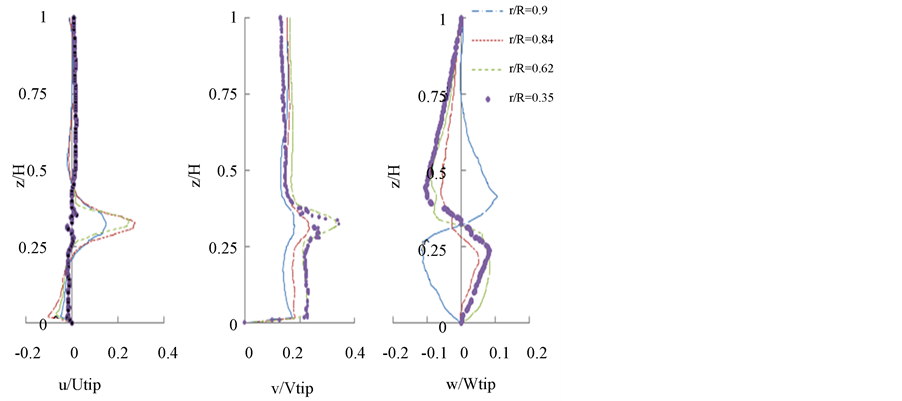
Figure 13 presents the axial profiles of the three components of the velocity at the angular position q = 15˚. In this position, four radial positions are studied. We note that the radial component of the velocity Figure 13(a) keeps the same appearance for all four radial positions. Except that the intensity of the velocity decreases away from the turbine with a maximum value of U/vtip = 0.3 for a radial position r/R = 0.5 to a value of U/vtip = 0.1 at r/R = 0.95. Figure 13(b) shows the profile of the tangential component of the velocity is established for the radial position r/R = 0.5. Beyond this radial position, we note that the tangential component of the velocity is almost constant. The axial evolution of the axial component of velocity is shown in Figure 13(c). These profiles are symmetrical in appearance: for r/R < 0.68 intense axial jet turbine fuels and for r/R > 0.8 it will reverse the side of the vessel wall.
5.6.2. Axial Profiles of the Velocity to an Angular Position q = 45˚
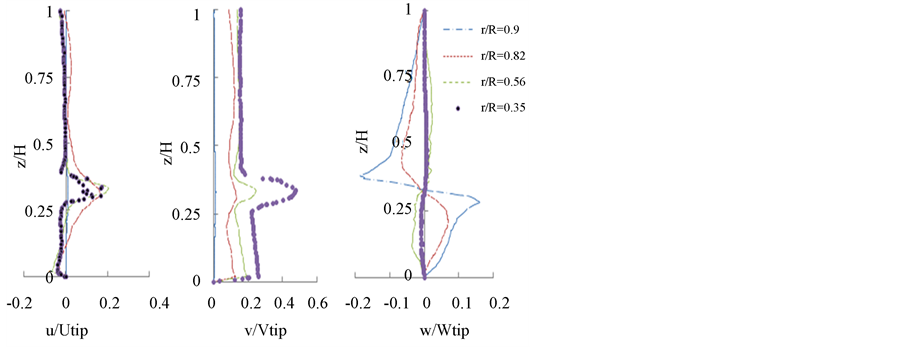
Figure 14 shows the axial profiles of the velocity for four positions. In Figure 14(a), the radial component of the radial velocity for this position is not affected by the geometry of the tank and the maximum values correspond to a radial position r/R = 0.84. Figure 14(b) presents the tangential component of velocity. This compo-
Figure 11. Distribution of turbulent viscosity in r-q plane.
Figure 12. Distribution of turbulent viscosity in r-q plane.
Figure 13. Axial profiles of velocity components at q = 15˚
nent is characterized by a value of velocity v/vtip = 0.2 which remains constant on both sides of the turbine. In the area swept by the impeller the tangential component presents the maximum value. This maximum is v/vtip = 0.4 at the radial position r/R = 0.62. Figure 14(c) shows the axial component of velocity. We find that the jet axial turbine that powers extends to a radial position r/R = 0.84. Note that for the radial position r/R = 0.9 the jet is weighty in descending lower zone of the tank but the jet ascending in the upper part is small and it’s zero in the axial position between z/H = 0.75 and z/H = 1.
5.6.3. Axial Profiles of the Velocity to an Angular Position q = 75˚
Figure 15 shows presents the evolution of the axial velocity at the angular position q = 75˚. Globally, we noted that the axial component decreases at r/R = 0.35 and r/R = 0.56. This decrease causes an increase of two other components in this region. Near the vessel tank, the axial component of velocity is intense and an axial jet ap- peared. For against, the two other components of velocity are very low.
6. Comparison with Experimental Results
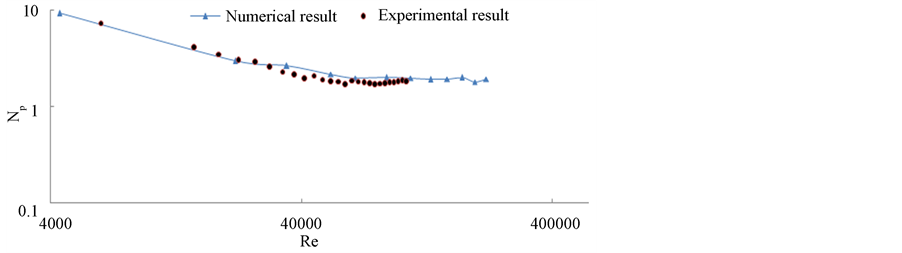
Using the house expérience, an experimental study was conducted to characterize the sturied tank. Specifically, we are interested in determining the variation of power number as a function of Reynolds number in the case of a square tank equipped with a standard Rushton turbine. To verify our computer results, the power number Np were measured and compared with the number calculated from the CFD code as shown in Figure 16. In this
Figure 14. Axial profiles of velocity components at q = 45˚.
Figure 15. Axial profiles of velocity components at q = 75˚.
Figure 16. Power number Np against reynolds number Re of rushton turbine in square tank.
comparison, the average error between the experimental results and the numerical results is equal to 5%. The good agreement confirmed the validity of the computer method.
7. Conclusion
A numerical study was performed to investigate the hydrodynamic structure generated by a six-blade Rushton turbine in a square vessel. To predict the effect of the tank design on the flow pattern, we have used the MRF approach with the rsm turbulent model. Particularly, we have presented the average velocity and the turbulent kinetic energy characteristics in different planes. To validate the CFD results, the power consumption of a stirred square tank equipped with Rushton impellers was predicted by using both experimental and simulation proceedings. This study needs further investigation both by experimental measurements of the local hydrody- namic with PIV technique and the development of the CFD method with the unsteady sliding mesh approach.
References
- Rushton, J.H., Costich, E.W. and Everett, H.J. (1950) Power Characteristics of Mixing Impellers. Chemical Engineer- ing Progress, 46, 467-476.
- Montante, G., Lee, K.C., Brucato, A. and Yianneskis, M. (2004) Numerical Simulation of the Dependency of Flow Pattern on Impeller Clearance in Stirred Vessels. Chemical Engineering Science, 56, 3751-3770. http://dx.doi.org/10.1016/S0009-2509(01)00089-6
- Montante, G., Mostek, M., Jahoda, M. and Magelli, F. (2005) CFD Simulations and Experimental Validation of Homogenisation Curves and Mixing Time in Stirred Newtonian and Pseudoplastic Liquids. Chemical Engineering Science, 60, 2427-2437. http://dx.doi.org/10.1016/j.ces.2004.11.020
- Derkson, J. (2002) Confined and Agitated Swirling Flows with Applications in Chemical Engineering. Flow Turbu- lence and Combustion, 69, 3-33. http://dx.doi.org/10.1023/A:1022419316418
- Armenante, P.M., Changgen, L., Chou, C., Fort, I. and Medek, J. (1997) Velocity Profiles in a Closed, Unbaflled Ves- sel: Comparison between Experimental LDV Data and Numerical CFD Redictions. Chemical Engineering Science, 52, 3483-3492. http://dx.doi.org/10.1016/S0009-2509(97)00150-4
- Alcamo, R., Micale, G., Grisafi, F., Brucato, A. and Ciofalo, M. (2005) Large-Eddy Simulation of Turbulent Flow in an Unbaffled Stirred Tank Driven by a Rushton Turbine. Chemical Engineering Science, 60, 2303-2316. http://dx.doi.org/10.1016/j.ces.2004.11.017
- Yeoch, S.L., Papadakis, G. and Yianneskis, M. (2005) Determination of Mixing and Degree of Homogeneity in Stirred Vessels with Large Eddy Simulation. Chemical Engineering Science, 60, 2293-2302. http://dx.doi.org/10.1016/j.ces.2004.10.048
- Nagata, S. (1975) Mixing Principles and Applications. John Wiley & Sons Halstead Press, Japan.
- Mazzarotta, B. (1993) Comminution Phenomena in Stirred Sugar Suspensions. A.I.Ch.E. Symposium Series, 89, 112-117.
- Bakker, A., Fasano, J.B. and Myers, K.J. (1994) Effects of Flow Pattern on the Solids Distribution in a Stirred Tank. IChemE Symp Series, No. 136, 1-8.
- Kilander, J. and Rasmuson, A. (2005) Energy Dissipation and Macro Instabilities in a Stirred Square Tank Investigated Using an LE PIV Approach and LDA Measurements. Chemical Engineering Science, 60, 6844-6856. http://dx.doi.org/10.1016/j.ces.2005.02.076
- Kresta, S.M., Mao, D. and Roussinova, V. (2006) Batch Blend Time in Square Stirred Tanks. Chemical Engineering Science, 61, 2823-2825. http://dx.doi.org/10.1016/j.ces.2005.10.069
- Kilander, J., Blomström, S. and Rasmuson, A. (2006) Rasmuson Spatial and Temporal Evolution of Floc Size Distri- bution in a Stirred Square Tank Investigated Using PIV and Image Analysis. Chemical Engineering Science, 61, 7651- 7667. http://dx.doi.org/10.1016/j.ces.2006.09.001
- Kilander, J., Blomström, S. and Rasmuson, A. (2007) Scale-Up Behaviour in Stirred Square Flocculation Tanks. Chemical Engineering Science, 62, 1606-1618. http://dx.doi.org/10.1016/j.ces.2006.06.002
- Brucato, A., Ciofalo, M., Grisafi, F. and Micale, G. (1998) Numerical Prediction of Flow Fields in Baffled Stirred Vessels: A Comparison of Alternative Modelling Approaches. Chemical Engineering Science, 53, 3653-3684. http://dx.doi.org/10.1016/S0009-2509(98)00149-3
- Aubin, J., Fletcher, D. and Xuereb, C. (2004) Modelling Turbulent Flow in Stirred Tanks with CFD: The Influence of the Modelling Approach, Turbulence Model and Numerical Schema. Experimental Thermal and Fluid Science, 28, 431-445. http://dx.doi.org/10.1016/j.expthermflusci.2003.04.001
- Bakker, A. and Oshinowo, L.M. (2004) Modelling of Turbulence in Stirred Vessels Using Large Eddy Simulation. Chemical Engineering Research and Design, 82, 1169-1178.
- Bakker, A., Oshinowo, L.M. and Marshall, E.M. (2000) The Use of Large Eddy Simulation to Eddy Simulation to Study Stirred Vessel Hydrodynamics. Proceeding of the 10th European Conference on Mixing, Delft, 2-5 July 2000, 247-254.
- Patankar, S.V. (1980) Numerical Heat Transfer and Fluid Flow. McGraw Hill, New York.
Nomenclature