Communications and Network
Vol.08 No.04(2016), Article ID:72287,16 pages
10.4236/cn.2016.84022
Physical Layer Deterministic Network Coding Using PUM Turbo Codes over AWGN Channel, N Nodes through a Base Station Scenario
Hani Attar
Department of Electronic and Electrical Engineering, Philadelphia University, Amman, Jordan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 26, 2016; Accepted: November 25, 2016; Published: November 28, 2016
ABSTRACT
Network Coding (NC) is a recent technique which is used to improve the transmission data rate and the power efficiency. These goals are obtained by combining data together before transmitting them, resulting to less transmitted data that carry the same amount of information. NC research work over the physical layer and the upper layers are popular and needed to be more investigated. In this paper, we propose a practical system of large-number of connected multi-source network coding (LMSNC), at the physical layer that exploits the broadcast nature of the wireless channel, using the practical and bandwidth-efficient schemes decode-and-forward (DF) and then compare it with Amplify and Forward (AF). The theoretical analysis and the simulation results show the effect of the noise when it cumulates in AF system and how DF is solving this severe default. Moreover, we consider the MSNC for Small-number of connected sources (SMSNC) and the two-way communication setup where two users exchange their information over an intermediate network node (ideally called Base Station), as two reference cases to compare with. With SMSNC, the number of necessary downlink transmissions from the intermediate node to the users is reduced, and thus the throughput is increased. Simulation results obtained using high-performance non-binary turbo codes, based on Partial Unit Memory (PUM) codes (4, 2, 1, 4) and (8, 4, 3, 8); confirm that combining PUM Turbo Code (PUMTC) and NC in the proposed MSNC setup gives almost the same BER performance as that for SMSNC at the small number of processing steps mainly when PUMTC (8, 4, 3, 8) is performed, which is required to retrieve the received coded messages. In the scenario of AF, combining packets results to cumulate the noise, which justifies the reason we decided to increase the number of transmitted coded messages in the network, i.e., the BER performance improves when sending extra coded messages. Finally, the possibility for a trade-off among BER, data rate and the number of transmitted coded messages is shown for LMSNC through graphics and simulation results.
Keywords:
Network Coding, Cooperative Nodes, Forward Error Correction

1. Introduction
Full-duplex, multi-hop communications, where users share their information simultaneously over a wireless radio channel, is becoming a popular communication setup. Applications range from data exchange, classic cell-phone voice conversations, interactive image/message exchange, file sharing, to wireless videophone/conference over 3G systems. An emerging scenario is transmission over multi-hop wireless ad hoc and sensor networks, where intermediate network nodes serve as relays.
Network coding (NC) [1] is a novel technique originally proposed for multicasting information over wireline networks of noiseless channels. NC is based on combining received information packets; that is, each intermediate NC node computes a certain encoding function of the received packets and forwards the resulting packet towards its destination. Strong potentials of NC in wireless packet networks were recently pointed out in [2] [3] [4] [5] and references therein. In [2] , a full-duplex channel model with two senders, two receivers, and one relay was studied, unlike the proposed work where a system with several number of nodes are propose together with BER performance analysis. [5] proposes a new coding algorithm that makes use of feedback to dynamically adapt the code (the three-receiver case). In [6] , channel coding and NC are combined for one-way communication with one intermediate relay node, however, the scenario in [6] does not show how to solve the problem of cumulative noise. In [7] , transmission schemes that enable a set of terminals to communicate with a common destination are proposed. Recently, two-way wireless communication was considered in [8] [9] [10] . In [8] a DF scheme based on distributed turbo code was used for protection: each user receives data from the relay and directly from the other user over two orthogonal channels; joint decoding is used for reconstruction for each user. The benefit of combining NC with convolutional codes via DF was shown in [8] , however, proposing NC over AF has not been discussed in [8] , which is a valuable contribution in this work. Another DF technique, which improves AF, was developed in [9] but for just two users, unlike this work which deals with any number of users. [10] proposes a channel code design that enables the decoder to operate at different effective rates by different receivers-rates, we added an important research to [10] by testing the decoding performance when changing the parameters of the same decoder, i.e., PUMTC for (4, 2, 1, 4) and (8, 4, 3, 8) to show that same encoder can give such different results. In [11] [12] practical schemes together with the capacity for amplify-and-forward (AF) and decode-and-forward (DF) schemes are proposed, for wireless full-duplex communications based on NC, using Partial Unit Memory-based Turbo Codes (PUMTC) and pseudo-random and quasi-cyclic regular Low-Density Parity-Check (LDPC) codes for exchanging information between two sources via a relay.
In this paper, we build upon [11] [12] by providing the framework for exchanging data among large number of connected sources for the proposed decode-and-forward DFp system, using the latest in turbo codes, i.e., non-binary PUMTC, and exploiting the broadcast nature of wireless radio links using NC. A generic framework for the practical schemes DFp, is proposed to exchange data among large number of multiple sources. Our proposed Multi-source NC (MSNC) scheme is compared to the classical setups and two-source NC [11] , and SMSNC assuming Additive White Gaussian Noise (AWGN) channels. We provide practical system designs based on a PUMTC using (4, 2, 1, 4) and (8, 4, 3, 8) PUM component codes. As a result of the good results obtained by our work in [11] ; we are extending using PUMTC over large number of users to show the behaviour of PUMTC under such scenario, beside to the fact of extending applying NC over more than two users.
Our work in [12] shows that applying PUMTC with NC over specific application such as wireless sensor network is such practical and power efficient design, however, yet extending the number of users in [12] was not solved when more than two packets are combined.
This paper is organized as follows. Section 2 describes the overall MSNC system setup and motivation, followed by the receiver-side operation in Section 3. Section 4 provides a case study for MSNC using four sources. In Section 5, we illustrate the relation between the data rate and the number of transmitted coded messages for different numbers of connected sources. In Section 6, we present our bit error rate (BER) results for MSNC together with a comparison with the two-source setup [11] . Section 7 concludes the paper.
2. DFp for LMSNC
Assuming that N users are exchanging data through one base station (BS) and each user generates its message mi, encodes it, and sends the resulting coded messages (CM) Xi where i = 1, 2, ∙∙∙, N over an uplink wireless channel to the BS that relays the received CMs Yi before broadcasting the transmitted CMs 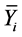 to the end users, which cannot overhear other signals. We assume that messages mi are uniformly distributed binary sequences that are transmitted over N uplink orthogonal channels.
to the end users, which cannot overhear other signals. We assume that messages mi are uniformly distributed binary sequences that are transmitted over N uplink orthogonal channels.
Traditionally, exchanging data between N sources requires broadcasting N2 − N transmitted CMs separately through the downlink channel. However, instead, the BS can apply a selective sum over the transmitted CMs (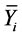 ) before broadcasting, where consecutive transmitted CMs are add, i.e.,
) before broadcasting, where consecutive transmitted CMs are add, i.e., 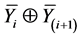 where i = 1, 2, ∙∙∙, N − 1 and Å is a modulo-2 operation. Accordingly, the BS needs to broadcast a minimum of N − 1 separate transmitted CMs to assure full connectivity for the N sources. This reduces the transmitted CMs through the downlink channel from N2 − N in the conventional communication system, (N2 − N)/2 in the two-source system [11] [12] [13] [14] , to N − 1 in the proposed MSNC system. Note that due to the asynchronous nature of the wireless channels, the N − 1 broadcasted transmitted CMs are assumed to reach the N receiving nodes simultaneously as received CMs
where i = 1, 2, ∙∙∙, N − 1 and Å is a modulo-2 operation. Accordingly, the BS needs to broadcast a minimum of N − 1 separate transmitted CMs to assure full connectivity for the N sources. This reduces the transmitted CMs through the downlink channel from N2 − N in the conventional communication system, (N2 − N)/2 in the two-source system [11] [12] [13] [14] , to N − 1 in the proposed MSNC system. Note that due to the asynchronous nature of the wireless channels, the N − 1 broadcasted transmitted CMs are assumed to reach the N receiving nodes simultaneously as received CMs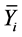 .
.
So, the larger connected sources the better data rate and power consumption, however, adding packets together means more cumulative noise and more complicated Jordan Gaussian Elimination (JGE) process, resulting to worse Bit Error Rate (BER) and more time delay. In this work, we first evaluate the disadvantage from applying NC over the physical layer, and then suggest our salutation to emigrate the effect of using NC over the physical layer.
The BER has a direct relation with the number of connected sources, as the more connected sources leads to more process steps and more error propagation.
To solve the problem of error propagation; DFp system is proposed in this case as decode-and-re-encode process performed at the BS reduces the noise level resulting in the uplink channel, and eventually minimizing error propagation. However, this decode-re-encode process exaggerates the problem of the time delay, which means that another improvement of the processing time delay is required, which is what this paper tickle as well.
As only a minimum of N − 1 transmissions are needed in LMSNC, this technique significantly decreases the power consumption compared to [11] [12] [13] [14] . Indeed, if we suppose that all transmitted CMs are bit streams of equal length, and each transmission consumes the same amount of power, then the broadcasted length of the transmitted CM is equal to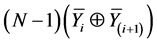 , where i = 1, 2, ∙∙∙, N, as each transmitted CM has the same length as that of the CM coded message e.g., Xi. Thus the transmitted power equals (N − 1)/(N2 − N) for N2 − N separate transmissions.
, where i = 1, 2, ∙∙∙, N, as each transmitted CM has the same length as that of the CM coded message e.g., Xi. Thus the transmitted power equals (N − 1)/(N2 − N) for N2 − N separate transmissions.
The BS decodes the received CMs 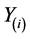 separately, and then the BS reconstructs the CMs Mi, re-encodes, modulates to
separately, and then the BS reconstructs the CMs Mi, re-encodes, modulates to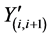 , selectively sums, and amplifies to N − 1 transmitted CMs
, selectively sums, and amplifies to N − 1 transmitted CMs 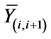 which are broadcasted separately, accordingly, just two packets are combined in this scenario to avoid the noise cumulative The received CM by the BS
which are broadcasted separately, accordingly, just two packets are combined in this scenario to avoid the noise cumulative The received CM by the BS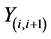 , the transmitted CMs
, the transmitted CMs 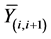 and the received CMs
and the received CMs 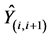 by N users, are given by Equations (1), (2) and (3) respectively.
by N users, are given by Equations (1), (2) and (3) respectively.
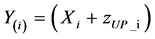 (1)
(1)
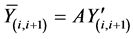 (2)
(2)
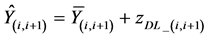 (3)
(3)
where 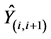 are the N − 1 reconstructed CMs from the sum of
are the N − 1 reconstructed CMs from the sum of 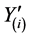 and
and 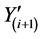 at the BS (i = 1, 2, ∙∙∙, N − 1), and
at the BS (i = 1, 2, ∙∙∙, N − 1), and  is the amplification coefficient of the proposed scheme. Note that the N − 1 received CMs
is the amplification coefficient of the proposed scheme. Note that the N − 1 received CMs 
This scenario has been applied over a cluster of wireless sensor network in [12] and showed how using NC if useful and both of power and data rate efficient.
3. Retrieving the Received Streams
As explained in DFp, the BS sums the N transmitted CMs consecutively, resulting in N − 1 combined transmitted CMs to be broadcasted simultaneously, so, they are received by the N users simultaneously as well.
Then, each receiver manipulates the received N − 1 combined CM 


where i = 2, 3, ∙∙∙, N with D1 being the receiver side, as an example, D1 starts retrieving






In order to retrieve 



Figure 1 shows the base station location in the network and the transmitted packets for the proposed scenario we are retrieving
The consecutive processing steps needed to retrieve the N estimated received messages at each user after receiving the transmitted packets by the BS (dashed arrows). At the receiver Dk, where k = 1, 2, ∙∙∙, N, there are two directions to retrieve





Figure 1. The proposed system for 4 users communicate through a BS, solid arrow is for direct transmission from users to BS and dashed arrows for the forwarded data from the BS to the four users.
Equation (5) and Equation (6) show the way to find the estimated CMs at the kth receiving side, starting from 





where 

where 
However, to reduce number of processing steps, additional transmitted CMs CT are needed, and are recommended to be chosen according to Equations (7) and (8) for the kth receiver side, where Equation (7) is used the reduce the number of processing steps needed in Equation (5), e.g., additional CMs to retrieve the estimated CMs starting from 




where i = 1, 2, ∙∙∙, (N ? k ? 1), and

where i = 1, 2, ∙∙∙, (N ? k ? 2).
An example for four MSNC is given in Section 4 to show the trade-off between performance and complexity when sending additional CMs.
4. Case Study: MSNC with Four Sources
In the following, we illustrate the concept of MSNC by means of an example where N = 4, with and without applying NC technique.
Assume four sources D1, D2, D3, and D4, exchange data, through a BS. Each source requests information from all other three sources. There is no direct connection between any of the pair of the sources. Thus all communication is performed via a BS, and with or without NC, as shown in Figure 2.
Figure 2 shows that six downlink transmitted CMs are needed to connect four sources using NC [11] [12] (Figure 2(b)). While twelve downlink streams are needed in conventional system (Figure 2(a)). In other word, two-source NC reduces the number of transmitted downlink CMs by 50% [11] [12] [13] , as the BS is represented in a set of relay nodes (R) with one relay for each connection that needs to be established.
In MSNC technique, a minimum of three downlink-transmitted CMs are sufficient to guarantee full connectivity between the four sources as shown in Figure 3.
In Figure 3, the three solid arrows represent the minimum required transmitted CMs, which give the lowest transmitted data rate, while the dashed lines represent the

Figure 2. A network of four sources that exchange data through BS/relay (R): (a) without NC or (b) with NC.
Figure 3. Four sources NC with N − 1 possible transmitted streams.
possible additional transmitted CMs to improve the BER at the cost of increased data rate. So, the first propose solution to the problem of noise propagation is to increase the number of NC combined packet. The relation between the data rate and BER is fully illustrated later on in this paper.
The other solution is to use the decode and re-encode DF at the BS as illustrated in Figure 4 illustrates the block diagram for the proposed system setup:
The nodes send the information to the Base Station after using PUMTC encoding as the forward error correction code.
PUM codes are dignified as a low-complexity alternative to the convolutional code which is one of the Shannon Limit Approaching codes. So, building turbo codes on PUM codes reduces the decoding complexity by reducing the number of the states in the trellis, a PUM code [15] is characterized by four parameters (n; k; μ; dfree), where n is the codeword length, k is the number of information bits to be encoded, μ is the memory (i.e., the number of bits in the shift register), and dfree is the minimum (free) distance between any two code sequences. Memory μ determines the state complexity of the code trellis diagram―the lower the μ the lower the decoding complexity. A convolutional code trellis is made up of μ states with 2k branches leaving and entering each state. For PUM codes, since k > μ, there are parallel branches between any two states in the trellis [15] .
In our systems, transmission is simulated over AWGN, using BPSK modulation for rate 1/3 PUMTCs based on (8, 4, 3, 8) and (4, 2, 1, 4) PUM component codes, and a pseudo-random interleaver of size 1000 bits.
After the encoding, the encoded data is amplified and then forward to the Base station through AWGN channel.
In DF Base Station as shown in the diagram; the received data from the node is first decoded using PUMTC decoder to remove the noise effect, and then combined with other users data (network coded), and then amplified and forwarded to the destination
Figure 4. Block diagram for the proposed system.
through AWGN channel.
At the destination, the combined packet is first decoded (PUMTC decoder), and then JGE is used to separate the combined packets using XORing operation to do so.
If the destination manages to retrieve the desired information, then it goes for the next transmission, otherwise the destination asks for ARQ for the same data.
In the result section; the BER for the benchmark and the network coded system is compared to first understand the behaviour of the PUMTC and then estimates the lost in the BER that results from combing the packets.
The proposed MSNC for four sources improves the power consumption as it requires only 25% and 50% of the power needed for systems without NC, and the two- source NC [11] [12] when N = 4, respectively.
Let us assume that D1 needs to retrieve 

So, to find









To understand the relation between the BER and data rate, an example for retrieveing 











In Figure 9, simulations results show improved BER performance for D1 when sending additional CMs at the cost of increased data rate. For example, data rate is increased from 3/12 to 5/12 when sending two additional transmitted CMs 

5. Transmitted Streams and Data Rate for MSNC
In this section, we show the relationship between the data rate and the number of transmitted CMs, for different number of connected sources. In Figure 5(a) and Figure 5(b), two sets of sources are used, for Figure 5(a) N = 3, 4, 5, 6, 7, 8, and 9 which is assumed to be the case of a small set of sources, while Figure 5(b) N = 10, 15, 20, 25, 30 and 50 is the case of large set of sources.
Moreover, as the two-source NC decreases the data rate by 50% compared with the
Figure 5. Data rate for (a) a small set of sources N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, (b) a large set of sources with N = 10, 15, 20, 25, 30 and 50.
conventional two-way communication system [11] [12] , simulation results for the proposed MSNC system at similar data rate of [11] is obtained for comparison. The number of transmitted CM starts from N ? 1 to (N2 ? N)/2(N ? 1), which is the minimum transmitted CMs for N connected sources to the number of transmitted CMs for the two-source NC which gives 50% data rate as shown in Figure 5.
Figure 5 shows that for a low number of sources, data rates increase rapidly towards 0.5 when the number of transmitted CMs is increased. This result is justified by the few number of CMs, which are available in the system. On the other hand, increasing the number of transmitted CMs using higher number of connected sources, e.g., 50 sources, results in minimal change in data rates.
Figure 6 shows the data rates corresponding to the minimum transmission streams in the proposed MSNC system. It is clear from Figure 6 that the MSNC improves the data rate, which means improving the power consumption. Note that sending just 49 CMs through the downlink channel for N = 50 connected sources in the BS gives just 0.02 data rate when compared with 0.5 for [11] , but the BER for such a low transmitted number of CMs is very high due to error propagation as 48 processing steps are needed to retrieve 

Finally, the chosen additional transmitted CMs depend on other factors beside the BER and data rate, such as the connection’s priority, in range/out range situation for
Figure 6. Data date at (N−1) for N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, 25, 30 and 50.
the connected sources, and the power consumption.
In order to clarify the effect of the additional transmitted CMs, in Section VI, BER results is provided for Equations (4), (5) and (6) connected sources at different number of transmitted CMs.
6. Simulation Results
Simulation results are obtained over AWGN channel, using binary phase shift keying (BPSK) modulation. Additionally, for both of (8, 4, 3, 8) and (4, 2, 1, 4) 1/3 PUMTC a pseudo-random interleaver of size 2000 bits is used. The BER performance curves are obtained by simulating transmission of at least 108 bits and that at least 100 frame errors are guarantee to be collected for statistical significance.
[11] is used to analyze the effect of varying the amplification factor and the number of turbo decoder iterations.
Figure 7 and Figure 8 show the relative BER performance when the iteration number (Iter) is increased from 2 to 8 in both of PUMTC (8, 4, 3, 8) AFp and DFp. This results in 1dB and 0.7 dB improvement in performance (Figure 7) at BER of 10−5 for AFp and DFp, respectively. However, in Figure 8 when the signal amplitude (Amp) is increased from 2 to 10 for PUMTC (4, 2, 1, 4) only 0.2 dB and 0.3 dB for AFp and DFp is observed, respectively. This improvement is justified by the performance of the used forward error correction PUMTC where the more iteration results to more corrections and hence better BER.
Moreover, Figure 7 and Figure 8 show that the DFp outperforms AFp by 2dB for (8, 4, 3, 8) compared to 3dB in (4, 2, 1, 4) at BER of 10−5, which is justified by the decoding-and-re-encoding processes performed at the BS. For sure, this is justified by removing the down link noise from the downlink channel from the users and the BS before forwarding the packets to the users.
Figure 7. BER performance for AFp and DFp PUMTC (8, 4, 3, 8) for Iter = 2, 4, and 8 at Amp =2 as benchmark scenario.
Figure 8. BER performance for AFp and DFp PUMTC (4, 2, 1, 4) for Amp = 2, 6, and 10 at Iter = 2 as benchmark scenario.
Similar observation regarding the AFp and DFp are noticed when the system is extended to MSNC, as shown in Figure 9 where DFp outperforms AFp by 3dB in (8, 4, 3, 8) and 3.8 dB in (4, 2, 1, 4) for the four sources MSNC at BER of 10−5.
Results obtained show that AFp for the two-source NC [11] [12] gives smaller BER than that of the proposed MSNC with AFp, which is expected and justified by the fewer number of the transmitted CMs, i.e., three transmitted CMs compared with six in [11] . In other word, [11] doubles the rate (or power) in the downlink when compared with N = 4 MSNC. Hence, at a BER of 10−5, two-source NC outperforms N = 4 MSNC by almost 0.6 dB with AFp (4, 2, 1, 4) and 1.6 dB with AFp (8, 4, 3, 8). However, the difference between the two techniques in the case of DF is significantly smaller, less than 0.2 dB for
Figure 9. BER vs. signal-to-noise ratio (SNR) in the downlink AWGN channel for N = 4 sources for AFp and DFp (4, 2, 1, 4) and (8, 3, 4, 8) for Iter = 4 and at Amp = 4.
(8, 4, 3, 8) at a BER of 10−5 and 0.1 dB for (4, 2, 1, 4) at the same BER. This is due to the decode-and-re-encode process performed at the BS to reduce the noise level resulting in the uplink channel as mentioned before, and eventually minimizing error propagation.
Finally, Figure 9 shows that increasing the number of connected sources from 4 to 6 results in minimal change in the BER performance almost 0.1 dB for (4, 2, 1, 4) at minimum transmission.
Similarly, the BER change in (8, 4, 3, 8) is totally negligible.
Figure 10 shows the improvement in the BER when the number of the transmitted CMs is increased. For N = 6 with (4, 2, 1, 4)-based PUMTC and four additional CMs an improvement of almost 1dB in (4, 2, 1, 4) is observed compared to the case of the minimum number of transmissions. This improvement of the BER is justified by the less retrieving steps and hence less aggregation noise. Note that each additional transmitted CM increases the total rate. This reflects the scheme scalable feature where each added transmitted CM (or layer) improves performance at the expense of increased data rate. Additionally, when 4 additional CMs are transmitted a performance similar to the two-source NC case is achieved.
For DFp, increasing the number of transmitted CMs does not improve the BER significantly as minimum transmission case almost matches the two-source case [11] ,
Figure 10. BER vs. SNR in the downlink AWGN channel AFp (4, 2, 1, 4) and (8, 4, 3, 8), N = 6 with the additional transmitted CMs for Iter = 4 and at Amp = 4.
and this is justified by the less noisy received packets by the users because the noise of the downlink from the users and the BS has been removed in earlier stage through the DF used at the BS. Hence, transmitting additional CMs is not beneficial at small number of connected sources (e.g., N = 4, 5, and 6).
7. Conclusions
In this paper, a MSNC that combines both PUMTC, with two different PUM code components (8, 4, 3, 8) and (4, 2, 1, 4), and NC for both AF and DF schemes is proposed to increase the throughput in a wireless multi-source network. Simulation results show that extending the two-source NC technique [11] [12] to the more challenging multi-source NC, results in significant improvement in data rate and only a minimal increase in BER performance compared to that of the two-source NC. On the other hand, MSNC achieves a similar BER performance to that of the two-source NC, however, at much lower data rates and required power consumption.
Finally, due to the relationship between the transmitted CMs and the data rate for the MSNC, increasing the number of connected sources results in minimal effect on BER performance, while increasing number of transmitted CMs has the major effect on BER performance and eventually the data rates.
In the future work, combining more packets at the physical layer is one of the main directions to go through to decrease the number of transmitted packets and hence understand the behaviour of the decoding process. Moreover, it is important to investigate the channel capacity accordingly.
One more important direction is to find practical protocols that can choose the best combination to make the retrieving steps as few as possible and hence decreasing the delay time resulting from the decoding processes.
Applying NC over the physical layer over practical real systems such as multiple access and real wireless application is an important direction to testify the benefit of the obtained improvement over real life, which is what is being investigated at the current time.
Acknowledgements
Philadelphia University deserves my acknowledgements for the good atmosphere. They maintain for their researchers and for the financial support for this research. Moreover, I am always thankful for Dr. Lina Stankovic and Dr. Vladimir Stakovic from the University of Strathclyde, Glasgow, UK, for their support with the technical issues, beside their proof reading and technical modifications in my whole research work. They always add good values for my research work.
Cite this paper
Attar, H. (2016) Physical Layer Deterministic Network Coding Using PUM Turbo Codes over AWGN Channel, N Nodes through a Base Station Scenario. Communications and Network, 8, 241-256. http://dx.doi.org/10.4236/cn.2016.84022
References
- 1. Ahlswede, R., Cai, N., Li, S.-Y.R. and Yeung, W. (2000) Network Information Flow. IEEE Transactions on Information Theory, 46, 1204-1216.
https://doi.org/10.1109/18.850663 - 2. Wu, Y., Chou, P.A. and Kung, S.-Y. (2005) Information Exchange in Wireless Networks with Network Coding and Physical-Layer Broadcast. Proceedings of CISS, Baltimore, March 2005.
- 3. Fragouli, C., Le Boudec, J.-Y. and Widmer, J. (2006) Network Coding: An Instant Primer. ACM SIGCOMM Computer Communication Review, 36, 63-68.
https://doi.org/10.1145/1111322.1111337 - 4. Sagduyu, Y.E. and Ephremides, A. (2005) Joint Scheduling and Wireless Network Coding. Proceedings of NetCod-2005, Riva del Garda, April 2005.
- 5. Sundararajan, J.K., Shah, D. and Medard, M. (2008) Online Network Coding for Optimal throughput and Delay—The Three-Receiver Case. ISITA-2008 International Symposium on Information Theory and Its Applications, Auckland, December 2008.
- 6. Hausl, C., Schreckenbach, F., Oikonomidis, I. and Bauch, G. (2004) Iterative Network and Channel Decoding on a Tanner Graph. Proc. Annual Allerton Conference on Communication, Control, and Computing, Monticello, October 2004.
- 7. Bao, X. and Li, J. (2006) A Unified Channel-Network Coding Treatment for User Cooperation in Wireless Ad-Hoc Networks. Proceedings of IEEE ISIT-2006, Seattle, 9-14 July 2006.
https://doi.org/10.1109/isit.2006.261833 - 8. Hausl, C. and Hagenauer, J. (2006) Iterative Network and Channel Decoding for the Two-Way Relay Channel. Proceedings of IEEE ICC’06, Istanbul, 11-15 June 2006.
https://doi.org/10.1109/icc.2006.255034 - 9. Popovski, P. and Yomo, H. (2006) The Ant-Packets Can Increase the Achievable throughput of a Wireless Multi-Hop Network. Proceedings of IEEE ICC’06, Istanbul, June 2006.
- 10. Xiao, L., Fuja, T.E., Kliwer, J. and Costello, D.J. (2006) Nested Codes with Multiple Interpretations. Proceedings of CISS’06, Princeton, 22-24 March 2006.
https://doi.org/10.1109/ciss.2006.286586 - 11. Attar, H., Stankovic, L. and Stankovic, V. (2009) Physical Layer Network Coding Based on PUM Turbo Codes. IEEE Mosharaka International Conference on Communications, Signals and Coding, Amman, January 2009.
- 12. Attar, H. and Stankovic, L. and Stankovic, V. (2012) Cooperative Network-Coding System for Wireless Sensor Networks. IET Communications, 6, 344-352.
- 13. Stankovic, V., Stankovic, L., Moinian, A. and Cheng, S. (2007) Wireless Full-Duplex Communications Based on Network Coding. Proceedings of 45th Annual Allerton Conference on Communications, Control and Computing, Monticello, September 2007.
- 14. Katti, S., Maric, I., Katabi, D., Goldsmith, A. and Medard, M. (2007) Joint Relaying and Network Coding in Wireless Networks. Proceedings of ISIT-2007, France, 24-29 June 2007.
https://doi.org/10.1109/isit.2007.4557120 - 15. Fagoonee, L. and Honary, B. (2005) Construction of Partial Unit Memory Encoders for Application in Capacity-Approaching Concatenated Codes. IEE Proceedings in Communications: Special Section on Capacity Approaching Codes, Design and Implementation, 152, 1108-1115.










