Communications and Network
Vol.5 No.3(2013), Article ID:35437,6 pages DOI:10.4236/cn.2013.53023
Transmission over Cognitive Radio Channel with Novel Secure LT Code
Department of Electrical Engineering (DCCS Lab), Iran University of Science and Technology, Tehran, Iran
Email: ehosseini@iust.ac.ir
Copyright © 2013 Elham Hosseini, Abolfazl Falahati. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 4, 2013; revised March 10, 2013; accepted April 10, 2013
Keywords: Cognitive Radio; Symmetric Cryptographic Key Generation; LT Code
ABSTRACT
With the increasing of communication applications in recent years, the demand for radio spectral resources has increased significantly. Cognitive radio scenario was proposed to improve spectrum efficiency in wireless communication systems. In cognitive radio network, it is essential that control information is sent securely and reliably. Ensuring the trustworthiness of the transmitting of spectrum sensing information is important in the CR networks since spectrum sensing directly affects spectrum management and incumbent coexistence. In this paper, the first secondary link channel model is presented, then a secure LT Code is proposed to be compatible with presented channel model and acquires good QoS. As we may know, LT code overcomes packet loss when the channel of the SU is reclaimed by PU. In the new proposed combined encoding and ciphered block, a LT code matrix is used to generate a symmetric cryptographic key. Thus, less complexity observed in the processing computation. Besides, cryptographic key is not sent over the channel. As a result, an attacker has no way to eavesdrop the key unless he is prepared to consider all possible key combinations. This replaced block supplies secure controlling channel and increases spectrum efficiency too.
1. Introduction
With explosive increase in demand for additional frequency spectrum, cognitive radios (CRs) were offered to support existing and new services. CR scenarios were proposed to improve spectrum efficiency and to solve the normally occurring spectrum scarcity. CR is also highly agile wireless platform, so it is capable of autonomously choosing operating parameters based on both frequency spectrum and network conditions. CRs promise an enhanced utilization of the limited spectral resources. In CR scenarios, secondary users (SUs) and primary users (PUs) coexist simultaneously [1-5].
The detection of PUs can be accomplished by opportunistic spectrum sharing [4,6]. In opportunistic spectrum sharing, the PU usage is automatically monitored by SUs based on CR scenario. In the CR scenarios, no changes have to be made to legacy systems as the PU is unaware of the secondary usage of its spectrum. Since the arrival of a PU acts like an erasure on the SU link, it causes the SU to lose all the packets that are being transmitted over the channel which was under that particular PU’s carrier. In order to overcome this problem caused by PU arrival on the SU link, some techniques have been proposed in [7]. In fact, any method to employ some sort of feedback procedures is not practical over CR network, indeed, once the channel has been captured by a PU, the retransmission request has to be placed on a different channel, which may not be available or reliable. So in order to avoid the need for a feedback channel, erasure-correcting codes are suggested [8]. Hence, the packets that are lost due to PU interference are now considered as erasures. The erasure-correcting codes used in our model are digital Fountain codes.
The concept of digital Fountain codes was first introduced by Byers et al. [9,10] in 1998 for information distribution. Fountain codes are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols. The original source symbols can ideally be recovered by the decoder from any subset of the received coded symbols of size equal to or only slightly larger than the number of source symbols. The term fountain or rate less refers to the fact that these codes do not exhibit a fixed code rate. In [11] a solution to further enhance the performance of cognitive radio networks is proposed.
LT codes were the first practical realization of fountain codes. This code was introduced for the purpose of scalable and fault-tolerant distribution of data over simplex channel like a computer network. Classification of erasure codes is shown in Table 1.
LT complexity of the encoding and decoding is very low [8]. Some networks, such as cognitive radio networks, do not have a feedback channel. Applications on these networks still require reliability. The SU link of cognitive radio can be modeled as a two states channel. One state is influenced by channel fading and noise but the other is like erasure channel. Thus, erasure code is a good choice for cognitive radio [12]. On the other hand, in cognitive radio network, it is normal to assume that there are no network attackers and the participants involved in the protocols are honest. But attackers always try to corrupt data anyway. As a result, a secure code is essential that can save time and cost.
As mentioned the successful deployment of CR networks and the realization of their benefits depend on the placement of essential security mechanisms in sufficiently robust form to resist misuse of the systems. Ensuring the trustworthiness of the spectrum sensing process is important in the CR networks, since spectrum sensing directly affects spectrum management and incumbent coexistence [13-17].
In this paper, secondary link channel model is presented and then secure LT code is proposed to supply security and reliability simultaneously. In the proposed block, a code matrix is used for generation of cryptographic key. Cryptographic key is not sent over the channel; as a result, the frequency spectrum is saved. Also coder information is used to generate cryptographic key.
The rest of this paper is organized as follows. In Section 2, we present the channel model of secondary link for cognitive radio. In Section 3, we discuss the proposed block and algorithm to generate symmetric cryptographic key. Simulation results and performance analysis are revealed is Section 4. Section 5 presents concluding remarks.
2. Secondary Link Channel Model for CR
The SU link can be modeled as a two states channel. In
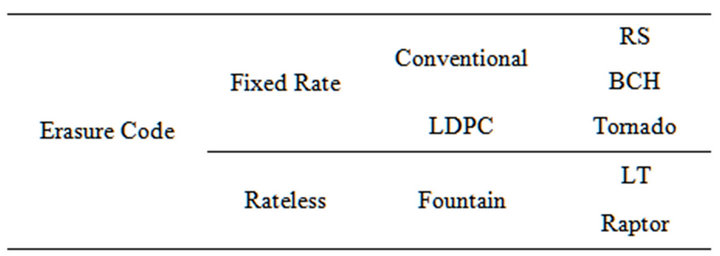
Table 1. Classification of erasure code.
the first state, channel is good. A channel is considered good if PU arrives after the duration of SU transmission and packets are lost due to channel fading and noise. In this state, a conventional method can be employed to improve the full system performance. In the other state, the channel is reclaimed by the PU during transmission of SU, then all packets transmitted over that channel after arrival of PU will be lost due to the evacuation of the SU. Hence, in order to recover these packets, some error correcting mechanisms are needed. In this state, the channel model can be assumed as erasure channel. The overall channel state diagram for the secondary link can now be observed by Figure 1.
Pij is the transition probability from state i to state j. Depending on the types of PUs, the primary traffic model may be different. In this paper, Primary User Arrival Model was assumed to be of a Poisson distribution.
P21 is probability density function (pdf) of at least one PU arrival during transmission of SU and can be given by:
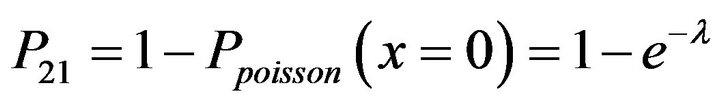 (1)
(1)
P22 is the pdf of that PUs do not request any service and can be given by:
 (2)
(2)
P11 is pdf of time duration that the channel is occupied by PU. P11 is exponential and its parameter ( ) depends on the type of the Primary network traffic.
) depends on the type of the Primary network traffic.
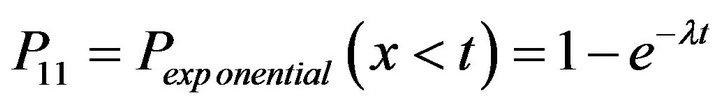 (3)
(3)
P12 is pdf of time that the channel is released by PU. This means that the transition probability is calculated from state 1 to state 2 after t second.
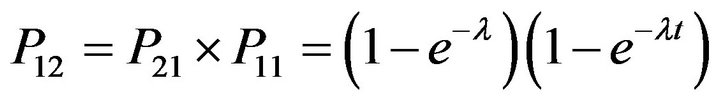 (4)
(4)
Channel states representations are shown in Figure 2. In this Figure pe1, pe2 are probability of error in the bad (BEC) and good (BSC) channel states respectively. Effective parameters in pe1 include channel fading, noise and interference of PU. But pe2 depends only upon channel fading and noise.
LT code is capable of providing protection from the

Figure 1. State Diagram of secondary link Channel (1: occupied channel, 2: ideal channel).
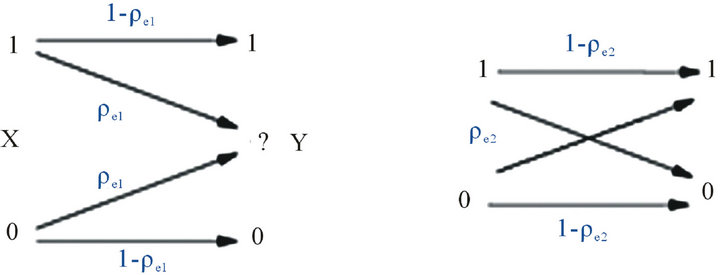
Figure 2. Channel states (a) State 1 (b) state 2. (a) Binary Erasure Channel; (b) Binary Symmetric Channel.
effects of packet loss irrespective of the loss model of the SU link. But the redundancy of the LT code causes to decrease the spectrum efficiency. In fact, in LT codes the reduction in spectrum efficiency is incompatible with the second state of the channel (i.e. good state). In order to improve the system’s performance a combined block is proposed here. Therefore, a secure LT code (SLC) is designed.
Two types of channels exist in cognitive radio network that are called control and traffic channels. Transmitted information over control channel influences on resource assignment. Thus, to hold good performance transmitted data, control channel should be protected against the attackers and distorting agents.
3. The Proposed Combined Encoding and Cyphering Block
In order to meet security and reliability over networks such as cognitive radio networks, secure LT code (SLC) is proposed. In this block, coder information is used to generate a sequence of (symmetric) keys k0, k1, …, kK. Combination of encryption and channel coder block decreases the required memory and processing time. Process of cryptographic key generation is followed from an algorithm completed by a few random numbers and an input random vector. In other words, a sequence of symmetric key is generated in the transmitter and the receiver and don’t need to be sent over the channel. Seed information of random generator is inserted to encrypted input data (X) in two ways. First, they are concatenated to X. In order to increase complexity, the header length can be selected variable periodically. And secondly, they are interleaved by a determined pattern.
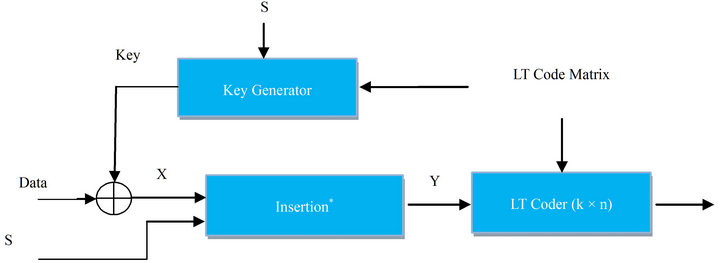
The block diagram of a secure LT coder is shown in Figure 3. In this block the cryptographic key is generated by the LT code matrix. Thus, overall system has less computation complexity. Besides, cryptographic key is not sent over channel. As a result, attacker has no way to eavesdrop the key, unless he is prepared to consider all possible key combinations. First, the data is encrypted, then the information including seeds of random generator and two random numbers are inserted into encrypted data. Finally Y is coded by LT channel coder to detect and correct error bits. In the receiver, all operations are inverted. In order to insert excess information, one can use a mask or concatenate method. Thus the mask vector must be known for both receiver and transmitter. The
 (a)
(a)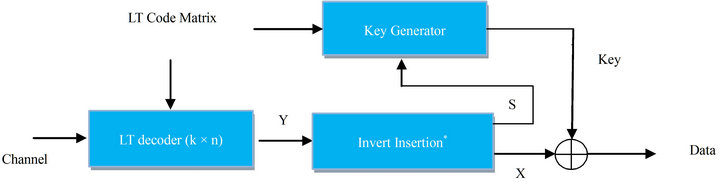 (b)
(b)
Figure 3. Combined block includes of cryptography and channel coding. (a) Transmitter schematic; (b) Receiver schematic.
block diagram of the transmitter and the receiver are shown in Figure 3.
SLC block has two advantages. First one is: a few bits (S packets) are sent instead of a symmetric cryptographic key to supply security of the link. The second advantage that SLC provides is the utilization of LT as error reduction as well as ciphering simultaneously. Indeed, the SLC improves the performance of the system significantly.
Key Generation Process and Management
In the proposed method, key is generated by the code matrix, a random vector and two separate random numbers. Process of key generation is done in both the receiver and the transmitter. In fact, the receiver knows the algorithm as well as receiving their seed values. Therefore, it is not essential to transmit cryptographic key through the channel.
In the designed combined block, the cryptographic symmetric key is generated with LT generator matrix and random numbers. According to the LT codes, its unique and revertible characteristics, the generated sequence of the key includes all possible combinations key. Flowchart for such a key generation is shown in Figure 4. This process can be followed as:
Step 1: A random vector is coded by generator matrix of LT code as.
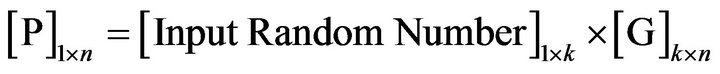
where G is the LT code matrix.
Step 2: Hash function is applied to the coded vector.

where the hash function can been selected arbitrary.
Step 3: The acquired vector is coded by section of generator matrix.
The selection of the section of the generator matrix The output dimension of the hash function is m bits. In order to encode output of the hash function (m bits), a segment of the LT matrix, with dimensions m × k, has to be selected. Then, two random numbers determine the row and column numbers of the segmented LT matrix.
k1, n1 are two random numbers determined from the beginning of the row and the columns of LT matrix (G)

Figure 4. Generation algorithm of matrix G1.
to select G1. When (k1 + m) and (n1 + k) exceed from k and n correspondingly, G is repeated twice in both dimensions to generate G1. G1 generation algorithm is depicted structurally and visually in Figure 4.
• Encoding the output of hash function by G1 to get the actual key:

Note: the selection of a section is done by substitution and permutation of the LT generator matrix. Information of this substitution, permutation, seed of random vector and the two random numbers will be transmitted in S packet.

4. Simulation Results
Performance of the key generator is considered via simulation process shown in Figure 5. Considering the struc ture of LT code matrix, we know that the coder has a unique output. Thus, the sequence of key achieved can be swept through all space of 2k. In order to consider performance of proposed key generation algorithm, simulation was done with the set of parameters followed.
4.1. Parameterization
1) LT codes: for LT codes, the degree distribution Ω (d)
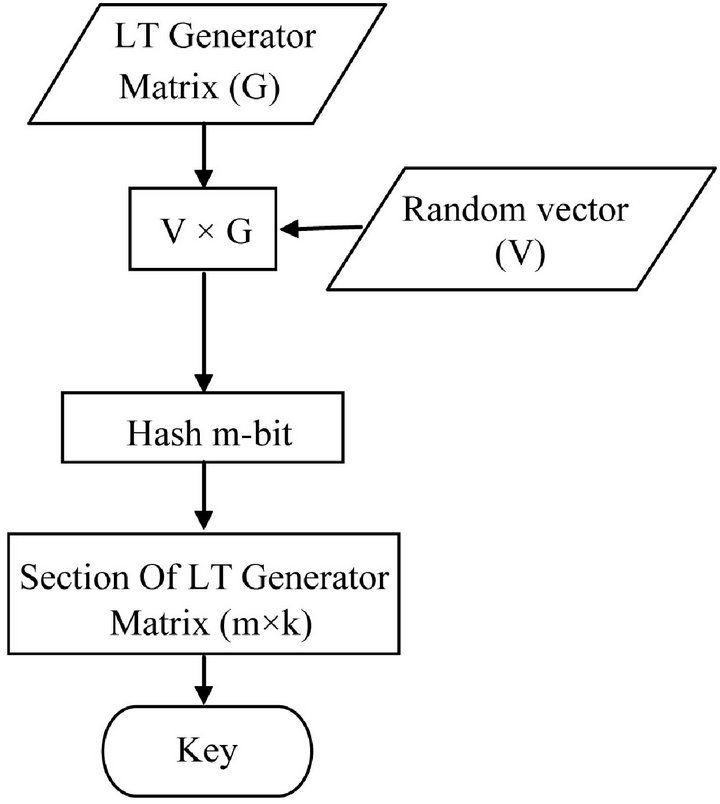
Figure 5. Flowchart of the key generator.
that we use is the robust Soliton distribution and is defined as follows. It has two parameters, σ and δ. The parameter δ is a bound on the probability that the decoding fails to run to completion. The parameter σ adjusts the size of ripple (S). In the paper, we take σ = 0.1, δ = 0.5, K = 1000, N = 2000. Now, define:
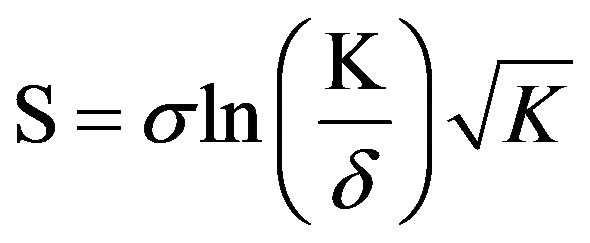 (5)
(5)
Then defined,
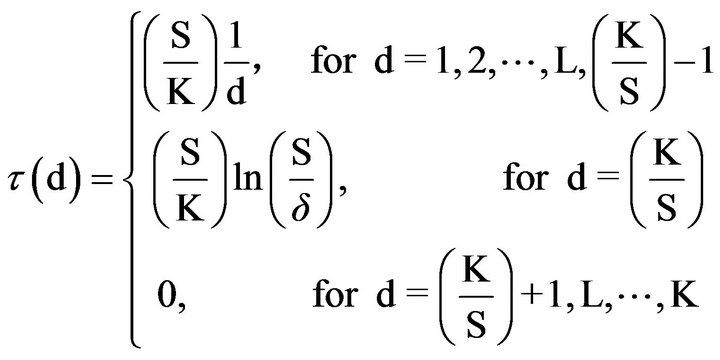 (6)
(6)
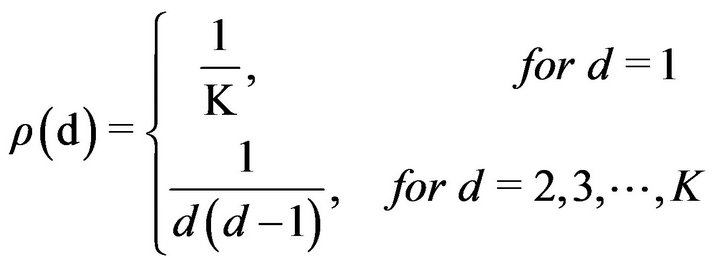 (7)
(7)
Then, the Robust Soliton Distribution is obtained by a linear combination of the Ideal Soliton Distribution and :
:
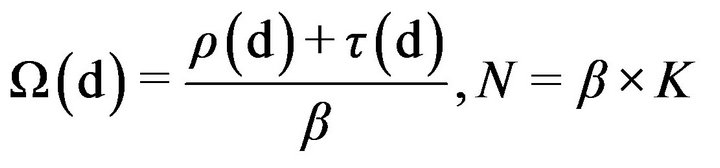 (8)
(8)
where  is normalization constant. Further discussion and reasoning for this distribution can be found in the references.
is normalization constant. Further discussion and reasoning for this distribution can be found in the references.
2) Random vector with uniform distribution as mask.
3) Hash function: SHA1 is used in simulation. But any hash function can be used.
4) Coding hash function output with section of LT generator matrix (m × k). Generation of two integer random number that indicated number of row and column.
r = randint (1, 1, [1, m])
c = randint (1, 1, [1, k])
5) Insertion pattern: simulation is carried out without pattern and seed information of random generator is concatenated to encrypted input data (X).
4.2. Performance Analysis
This method is resistant against all type of attacks except Brute-Force. Of course, the complexity of the Brute Force attack is highly relative to the available time of the attacker. The number of operators increases exponenttially by k input packets. n, k, m are numbers of coded packets, number of input packet, and length of hash functions output respectively. The number of key combinations for Brute-Force attack is computed from Equation (9).
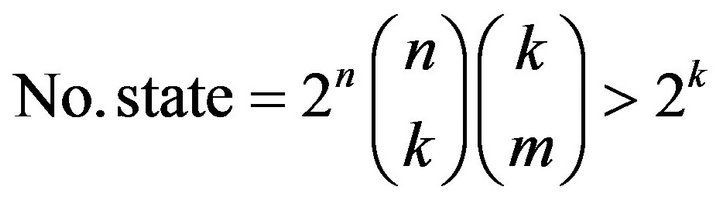 (9)
(9)
According to the number key states and LT code properties, unique and reversible, it can be concluded that the cryptography key is pseudorandom.
5. Conclusion
The importance of security in a cognitive radio network must highly be recognized. Since CR scenario permits attackers to easy and unauthorized access. First of all, secondary link channel model is proposed and a combinational block is proposed for a secure LT code, as well as providing security and error correction capability simultaneously. In SLC, a generator matrix is used to generate a random cryptographic key. SLC supply security without transmitting the key in a symmetric cryptography in a secure channel, as a result, the increase in spectrum efficiency becomes apparent. This implies saving time and costs. Besides, the key does not appear on channel, consequently, the attackers have to consider all possible key combinations. This block is useful in all communication systems that have no feedback channel.
REFERENCES
- L. B. Wang and K. J. Ray Liu, “Advances in Cognitive Radio Networks: A Survey,” IEEE Journal of Selected Topics in Signal Processing, Vol. 5, No. 1, 2011, pp. 5- 23.
- N. Devroye, P. Mitran and V. Tarokh, “Limits on Communications in a Cognitive Radio Channel,” IEEE Communications Magazine, Vol. 44, No. 6, 2006, pp. 44-49. doi:10.1109/MCOM.2006.1668418
- Q. Zhao and B. M. Sadler, “Dynamic Spectrum Access: Signal Processing, Networking, and Regulatory Policy,” IEEE Signal Processing Magazine, Vol. 24, 2006, pp. 79-89.
- R. Etkin, A. Parekh and D. Tse, “Spectrum Sharing for Unlicensed Bands,” IEEE Journal on Selected Areas in Communications, Vol. 25, No. 3, 2005, pp. 517-528.
- S. Haykin, “Cognitive Radio: Brain-Empowered Wireless Communications,” IEEE Journal on Selected Areas Communications, Vol. 23, No. 2, 2005, pp. 201-220. doi:10.1109/JSAC.2004.839380
- A. Nosratinia, T. E. Hunter and A. Hedayat, “Cooperative communication in wireless network,” IEEE Communications Magazine, Vol. 42, No. 10, 2004, pp. 68-73. doi:10.1109/MCOM.2004.1341264
- S. Somasundaram and K. P. Subbalakshmi, “3-D Multiple Description Video Coding for Packet Switched Networks,” Proceedings of the IEEE International Conference on Multimedia and Expo, Baltimore, 6-9 July 2003, pp. 589-592.
- M. Luby, “LT Codes,” Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, November 2002, pp. 271-282.
- J. W. Byers, M. Luby, M. Mitzenmacher and A. Rege, “A Digital Fountain Approach to Reliable Distribution of Bulk Data,” Proceedings of ACM SIGCOMM’98, Vancouver, September 1998, pp. 56-67.
- D. J. C. MacKay, “Fountain Codes,” IEEE Communications, Vol. 152, No. 6, 2005, pp. 1062-1068.
- K. V. Goenka and R. D. Raut, “Application of Fountain Codes to Cognitive Radio Networks and MBMS—A Review,” International Journal of Computer Applications (0975-8887), Vol. 66, No. 14, 2013, pp. 28-30.
- H. Kushwaha and R. Chandramouli, “Secondary Spectrum Access with LT Codes for Delay Constrained Applications,” Proceedings of the IEEE Consumer Communications and Networking Conference, Las Vegas, January 2007, pp. 1017-1021.
- A. Ghasemi and E. S. Sousa, “Collaborative Spectrum Sensing for Opportunistic Access in Fading Environments,” Proceedings of IEEE International Symposium on New Frontier in Dynamic Spectrum Access Network, Baltimore, 8-11 November 2005, pp. 131-136.
- F. Digham, M.-S. Alouini and M. K. Simon, “On the Energy Detection of Unknown Signals over Fading Channels,” IEEE Transactions on Communictions, 11-15 May 2003, pp. 3575-3579.
- G. Ganesan and Y. Li, “Cooperative Spectrum Sensing in Cognitive Radio Networks,” Proceedings of IEEE International Symposium on New Frontier in Dynamic Spectrum Access Network, Baltimore, 8-11 November 2005, pp. 137-143.
- H. Urkowitz, “Energy Detection of Unknown Deterministic Signals,” Proceedings of the IEEE, Vol. 55, No. 4, 1967, pp. 523-531. doi:10.1109/PROC.1967.5573
- S. Cheng, V. Stankovic and L. Stankovic´, “An Efficient Spectrum Sensing Scheme for Cognitive Radio,” IEEE Signal Processing Letters, Vol. 16, No. 6, 2009, pp. 501- 504.

