Communications and Network
Vol.3 No.1(2011), Article ID:3988,6 pages DOI:10.4236/cn.2011.31003
Statistical Recognition Method of Binary BCH Code
Institute of Electronic Engineering in China Academy of Engineering Physics, Mianyang, China
E-mail: hugeghost@hotmail.com
Received October 30, 2010; revised January 5, 2010; accepted January 6, 2011
Keywords: binary BCH code, blind recognition, code length, generator polynomial
Abstract
In this paper, a statistical recognition method of the binary BCH code is proposed. The method is applied to both primitive and non-primitive binary BCH code. The block length is first recognized based on the cyclic feature under the condition of the frame length known. And then candidate polynomials are achieved which meet the restrictions. Among the candidate polynomials, the most optimal polynomial is selected based on the minimum rule of the weights sum of the syndromes. Finally, the best polynomial was factorized to get the generator polynomial recognized. Simulation results show that the method has strong capability of anti-random bit error. Besides, the algorithm proposed is very simple, so it is very practical for hardware implementation.
1. Introduction
With the development of the Communication Countermeasures, the methods of the communication countermeasures have transferred from the signal level to the information level. The blind recognition of channel coding is the foundation of getting the message, therefore has become the key technology in the area of the Communication Countermeasures and gets more and more attention. Besides, the blind recognition of channel coding also has important applications in cooperative areas such as the intelligent communication.
The linear channel coding has two categories: block code and convolutional code. We can see that most researches focus on the blind recognition of convolutional code [1-2], while literature about the blind recognition of block code is rare. Literature [3] gives a blind recognition method of the block code with low encoding rate, its essential principle is to resolve equations to recognize the syndrome matrix, and then get the generator matrix. Literature [4] discusses a method of blind recognition of primitive RS code, its essential principle is using reduced row echelon form of the matrix (RREF), fault-tolerant matrix decomposing (FTMD) and Galois field Fourier transform (GFFT) to recognize encoding parameters and syndrome matrixes. Both methods need matrix computations on the finite field, when code length is long, the EMS memory needed will be very large, so it is not applicable to hardware implementation. At the same time, the error code capability is not ideal too.
In this paper we study the binary BCH code which is an important subclass of cyclic codes. According to the circular feature, we proposed a simple statistical recognition method under the condition that the frame length is known. The method has strong anti-error capability. Besides, there is no need for matrix computation; therefore it is suitable for hardware implementation.
The reset of this paper is organized as follows: Section 1 introduces the basic feature of binary BCH code; Section 2 discusses the recognition method of the block length; Section 3 discusses the method of recognition of the generator polynomial; Section 4 observes the recognition performance of this algorithm through simulation; finally, the paper is briefly summarized.
2. Binary BCH Code
Here we simply introduce the features of binary BCH code. The definition of binary BCH code and the details of encoding and decoding are discussed in literature [5].
Consider (n,k) BCH code defined on GF(2), n is the block length and k is the message length. Let  be the message word before encoding,
be the message word before encoding,  be the code word after encoding, because it is the cyclic code, the message word and code word each has a corresponding message polynomial and code polynomial defined on GF(2), as follows
be the code word after encoding, because it is the cyclic code, the message word and code word each has a corresponding message polynomial and code polynomial defined on GF(2), as follows
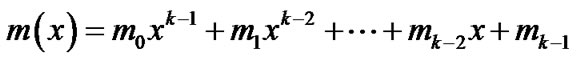 (1)
(1)
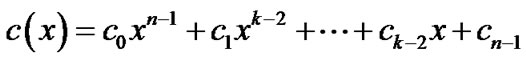 (2)
(2)
From literature [5], we know that the (n,k) binary BCH code has following features
1) Block length n equals  or is a factor of
or is a factor of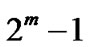 , where
, where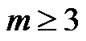 . If n equals
. If n equals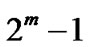 , then it is primitive binary BCH code; otherwise, it is nonprimitive one.
, then it is primitive binary BCH code; otherwise, it is nonprimitive one.
2) The code word c satisfies the circular feature, that is, after circular shifting the code word c for j times, get the code word

and  also belongs to (n, k) binary BCH code set.
also belongs to (n, k) binary BCH code set.
3)  and
and 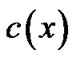 satisfy following relationship,
satisfy following relationship,
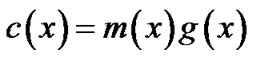 (3)
(3)
where  is the generator polynomial defined on GF (2),
is the generator polynomial defined on GF (2),
 (4)
(4)
4) There exists syndrome polynomial  defined on GF(2),
defined on GF(2),
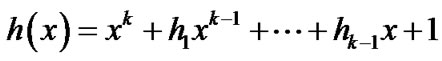
 (5)
(5)
which satisfies following relationships,
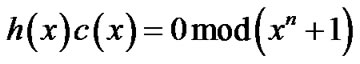
 (6)
(6)

 (7)
(7)
5) 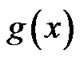 is irreducible.
is irreducible.
3. Recognition of Block Length
The recognition of the binary (n, k) BCH code is to recognize three parameters: the block length n, the syndrome word length k, and the generator polynomial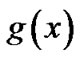 . But we can see from formula (4) that the order of
. But we can see from formula (4) that the order of  is n-k, then as long as the block length n and the generator polynomial
is n-k, then as long as the block length n and the generator polynomial 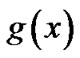 are recognized, the value of k can be ascertained. Then only the block length n and the generator polynomial
are recognized, the value of k can be ascertained. Then only the block length n and the generator polynomial 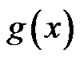 need to be recognized. In this section we introduce the recognition of block length n, and in next section we introduce the recognition of generator polynomial
need to be recognized. In this section we introduce the recognition of block length n, and in next section we introduce the recognition of generator polynomial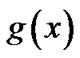 .
.
The recognition is based on the assumption that frame length  is known. This assumption is rational, because usually in practice, frame head is not encoded, so it is easy to get.
is known. This assumption is rational, because usually in practice, frame head is not encoded, so it is easy to get.
Because  is known, and there exists at least two code words in one frame, so we could get following conclusions:
is known, and there exists at least two code words in one frame, so we could get following conclusions:
1)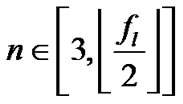 , where
, where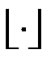 means floor function.
means floor function.
2)  is divisible by n, that is, n is a factor of
is divisible by n, that is, n is a factor of .
.
The factor numbers of 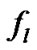 in the rang
in the rang 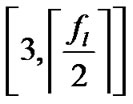 may not be only one, assume
may not be only one, assume  is a factor of
is a factor of  and then there are two situations
and then there are two situations
1) 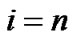
Under this situation, if we take i as the block length, we could get  code words. Assume
code words. Assume 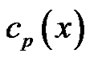 is the code polynomial of the
is the code polynomial of the  th code word, then through left circular shifting for j times we get j code polynomials
th code word, then through left circular shifting for j times we get j code polynomials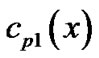 ,
, 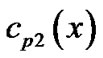 ,
,  ,
, 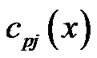 , where
, where .
.
Because the binary BCH code satisfy the circular feature, if there is no error code in , then the code words corresponding to
, then the code words corresponding to ,
, 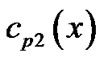 ,
,  ,
, 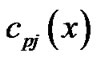 and the code word corresponding to
and the code word corresponding to  belong to the same (n, k) binary BCH set, so their generator polynomials are the same. According to formula (3) which is the relationship between the code polynomial and the generator polynomial, we know there is a common factor for
belong to the same (n, k) binary BCH set, so their generator polynomials are the same. According to formula (3) which is the relationship between the code polynomial and the generator polynomial, we know there is a common factor for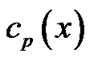 ,
,  ,
, 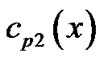 ,
,  ,
,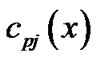 . Let
. Let  , then the following relationship exists,
, then the following relationship exists,
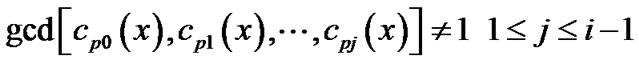 (8)
(8)
We call the code word that satisfies fomula (8) as a valid code word. Assume there are  valid code words among the
valid code words among the  code words. Obviously, when there is no error code,
code words. Obviously, when there is no error code,  , that is, the percentage of the valid code words of all the code words
, that is, the percentage of the valid code words of all the code words  is,
is,
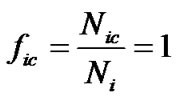 (9)
(9)
2) 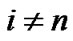
Under this situation, if we take i as the block length, the blocking is wrong. Assume we get 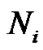 code words, there exist code words that do not satisfy formula (8) inevitably, so
code words, there exist code words that do not satisfy formula (8) inevitably, so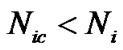 , that is
, that is
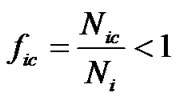 (10)
(10)
Above all, under the condition that no error code exists, if take formula (8) as the rule to judge if the code word is valid or not, then for all the possible block lengths, when , the percentage of valid code words is
, the percentage of valid code words is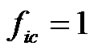 ; when
; when , the percentage of valid code words is
, the percentage of valid code words is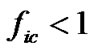 . Of course, when there are error codes exist, even if
. Of course, when there are error codes exist, even if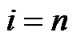 ,
, 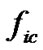 could be less than 1. But we can predict that
could be less than 1. But we can predict that 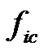 should get the maximum when
should get the maximum when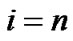 .
.
In addition, according to feature (1), n is odd , so we could get the recognition formula of the block length n,
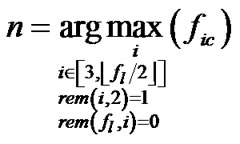 (11)
(11)
where  means the maximum operation;
means the maximum operation;  means the remainder of
means the remainder of 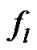 divided by i. The rule to judge the validity of the code word is formula (8). Then we can get the recognition process of binary BCH code block length n:
divided by i. The rule to judge the validity of the code word is formula (8). Then we can get the recognition process of binary BCH code block length n:
1) Let 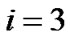 and initialize the value of j;
and initialize the value of j;
2) If 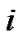 can not divide
can not divide , then turn to (6);
, then turn to (6);
3) Let 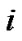 be the block length and get
be the block length and get  code words;
code words;
4) According to formula (8), calculate the number of valid code words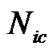 ;
;
5) Compute  and save;
and save;
6) ;
;
7) If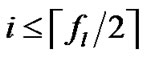 , turn to (2);
, turn to (2);
8) Compare all the saved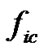 , the estimation of n is
, the estimation of n is  that made
that made 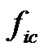 has maximum value;
has maximum value;
9) The recognition process is over.
We can see from step (11) and step (8), the recognition capability of block length n is relevant to  and
and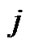 , the more the value of
, the more the value of  and
and , the better the recognition capability at the first glance; but large values mean that the length of the received code stream series is also large, and the computation complexity will increase, so we must consider this tradeoff according to the practical situations.
, the better the recognition capability at the first glance; but large values mean that the length of the received code stream series is also large, and the computation complexity will increase, so we must consider this tradeoff according to the practical situations.
4. Recognition of Generator Polynomial
In this section, we discuss how to recognize the generator polynomial 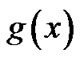 under the condition of the block length n is rightly recognized.
under the condition of the block length n is rightly recognized.
Assume we receive N code words, 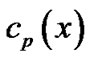 is the code polynomial for the
is the code polynomial for the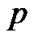 th code word, and assume that there is no error code. According to section II, left circular shift
th code word, and assume that there is no error code. According to section II, left circular shift  to get n−1 code polynomials
to get n−1 code polynomials ,
, 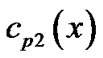 ,
,  ,
,  , and the generator polynomials of these n−1 code polynomials and
, and the generator polynomials of these n−1 code polynomials and  are the same. In other words, the generator polynomial
are the same. In other words, the generator polynomial 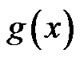 is a common factor of
is a common factor of ,
, 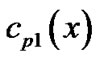 ,
, 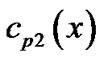 ,
,  ,
,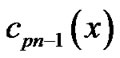 . Also let
. Also let , and
, and
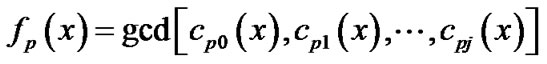 (12)
(12)
Then  is the multiple of
is the multiple of .
.
From the received N code words, we can get M ( ) different polynomials according to formula (12), consider there are error codes, these M polynomials belong to one of the four situations below:
) different polynomials according to formula (12), consider there are error codes, these M polynomials belong to one of the four situations below:
1) Equal 1;
2) Not equals 1, but not equals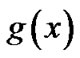 , also not the multiple formula of
, also not the multiple formula of ;
;
3) Equal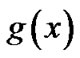 ;
;
4) Equal the multiple formula of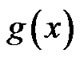 .
.
Situations (1) and (2) illustrate there are error codes exist. Situations (3) and (4) illustrate there are no error codes exist in code words, or the error codes constitute another code words in the same sub code set. We can get the generator polynomial from the M candidate polynomials following three steps below.
Step 1. According to the constraint conditions of 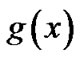 satisfied, remove the polynomials that do not satisfy the conditions According to the feature of the binary circular code,
satisfied, remove the polynomials that do not satisfy the conditions According to the feature of the binary circular code,  needs to satisfy the following restrictions [5]1)
needs to satisfy the following restrictions [5]1) 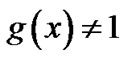
2)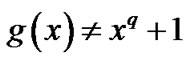 , where
, where  is the positive integer and
is the positive integer and 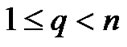
3) 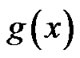 can divide
can divide 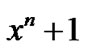
According to these three restrictions to remove the polynomials under situations (1) and (2).
Step 2. According to the minimum rule of the weights sum of the syndromes choose the most optimal polynomial Assume after the step 1 there are L candidate polynomials remain, and  (
( ) is the ith polynomial, and its corresponding syndrome polynomial is,
) is the ith polynomial, and its corresponding syndrome polynomial is,
 (13)
(13)
The jth syndrome of the code word is,
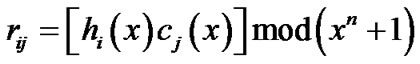 (14)
(14)
The code weight is,
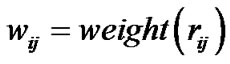 (15)
(15)
For all the received N code word compute the syndrome code weight,
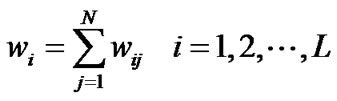 (16)
(16)
The candidate polynomial made  minimum is the most optimal polynomial, denotes as
minimum is the most optimal polynomial, denotes as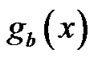 ,
,
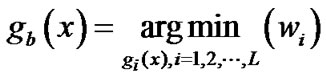 (17)
(17)
Step 3. From the most optimal polynomial  to get the estimated generator polynomial
to get the estimated generator polynomial .
.
When the reorganization is correct, the most optimal polynomial  is not necessarily equals
is not necessarily equals , but it is definitely the multiple of
, but it is definitely the multiple of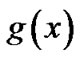 , so further steps are needed using
, so further steps are needed using 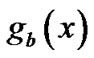 to estimate the generator polynomial.
to estimate the generator polynomial.
Firstly according to the rules in [6], judge whether 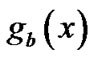 is reducible or not; if it is irreducible, then
is reducible or not; if it is irreducible, then
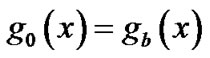 (18)
(18)
If it is reducible, get all the irreducible factor of v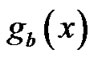 that satisfy step 1, then follow step 2 to get the most optimal polynomial as the estimated generator polynomial
that satisfy step 1, then follow step 2 to get the most optimal polynomial as the estimated generator polynomial . The method of factorization can indirectly get from the rules in [6], we do not comment on this because the limitation of space.
. The method of factorization can indirectly get from the rules in [6], we do not comment on this because the limitation of space.
From the above recognition process, theoretically, as long as there is a code word without error code, it is of very high possibility to correctly recognize the generator polynomial, then this recognition method has strong anti-error capability.
5. Simulation
The simulation has three steps: first, we simulate for the recognition capability of the block length; second, we simulate for the recognition capability of the generator polynomial; third, according to the first two steps we get the total recognition capability.
In the simulation of the recognition capability, we run the simulation 1000 times for (15,11) primitive binary BCH code and (21,12) non-primitive binary BCH code respectively to get the statistical correct recognition rate. The generator polynomial of (15,11) primitive binary BCH code is ; the generator polynomial of (21,12) non-primitive binary BCH code is
; the generator polynomial of (21,12) non-primitive binary BCH code is ;assume that there are five code words in one frame, and we choose the circular shifting time as 1 for recognizing the block length.
;assume that there are five code words in one frame, and we choose the circular shifting time as 1 for recognizing the block length.
5.1. Simulation Results
The recognition simulations are done according to the method described in Sections 2 and 3. The results are shown in figures 1-6. The total recognition capability is computed according to the block length recognition capability and generator length recognition capability, the computation formula is as follows,
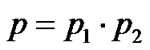 (19)
(19)
where 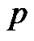 is the total correct recognition rate,
is the total correct recognition rate,  is the correct recognition rate of block length,
is the correct recognition rate of block length,  is the correct recognition rate of generator polynomial.
is the correct recognition rate of generator polynomial.
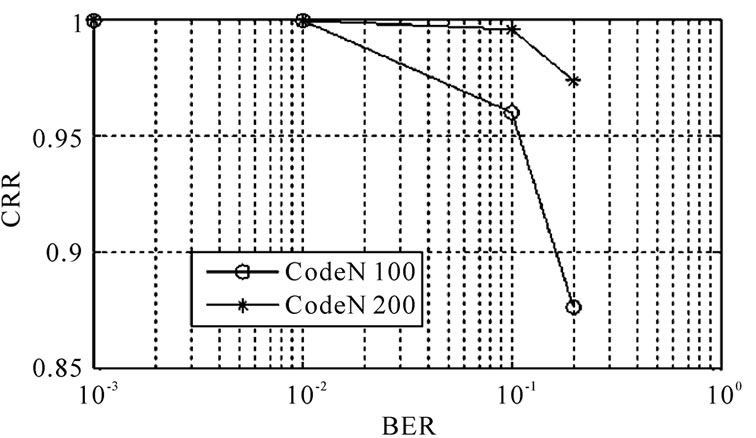
Figure 1. (15,11) code block length recognition capability.
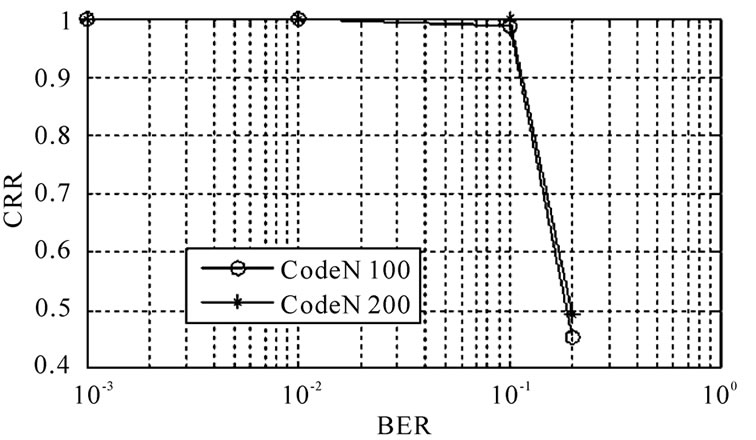
Figure 2. (15,11) code generator polynominal recognition capability.

Figure 3. (21,12) code block length recognition capability.
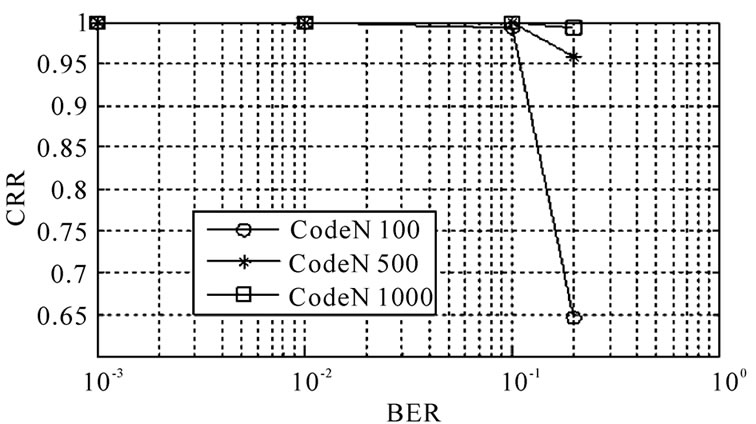
Figure 4. (21,12) code generator polynominal recognition capability.

Figure 5. (15,11) code total recognition capability.
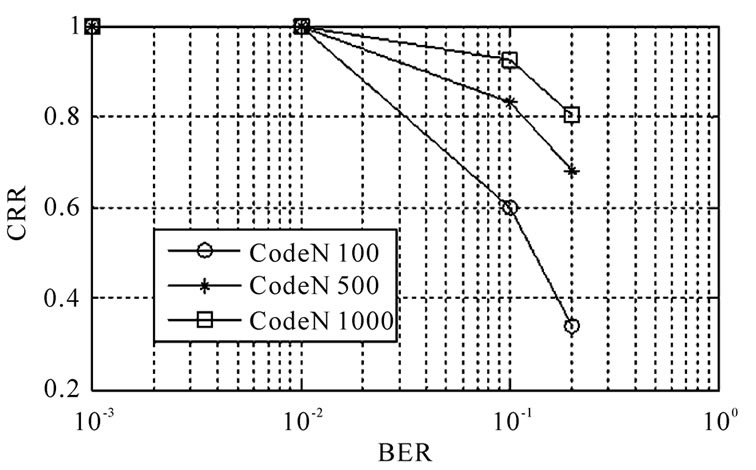
Figure 6. (21,12) code total recognition capability.
Note: In pictures, BER represents “Bit Error Rate”, CRR represents “Correct Recognition Rate”, and CodeN repesents “Code-words Number”.
5.2. Analysis of Simulation Results
From the results of the simulation, we know that no matter the recognition capability of the block length, the recognition capability of the generator polynomial, or the total recognition capability, will increase with the number of code words that are used for the recognition process. The recognition capability will also increase with the circular shifting time. Because of the limitation of space, the simulation results are not given here.
Otherwise, we can see that under the condition of the number of code words is the same, the difference between the recognition capability of these two kinds of code words is relatively large. For (15,11) code, when the error code rate is 10%, 100 code words are used , its total recognition capability could reach above 90%. While for (21,12) code, when the error code rate is the same, to reach the same recognition capability, we need 1000 code words. The reason for this difference is various1) The code length of (21,12) code is longer than (15,11) code, then when the code words is the same, through a circular shift, the percentage of satisfying circular feature would be higher than (15,11) code, even if not right blocking.
2) The frame length of (21,12) code is 105, it has 6 odd factor: 3, 5, 7, 15, 1, 35; while the frame length of (15,11) code is 75, it has 4 odd factor: 3, 5, 15, 25. Obviously, when the code word number is the same, the more the factor, the worse the recognition capability.
Of course, the recognition capability is also relevant to the structure of the code, (15,11) code is primitive binary BCH code and (21,12) code is non-primitive binary BCH code. But we can see from the simulation result, although when the number of code words is the same, the recognition capability of (21,12) code is worse than (15,11) code, but we can increase code words to reach the same recognition capability .
6. Conclusions
The blind recognition method of the binary BCH code proposed in this paper is a statistical recognition method. So the recognition capability is directly related to statistical bit number, the more the statistical bits, the better the recognition capability and the bigger the computation complexity, especially under the condition of long code, which is a drawback of the algorithm proposed in this paper. But when compared to its recognition capability, the big computation complexity is acceptable. Besides, the algorithms in this paper do not involve complicated computations, and it could be readily applied to the hardware processor because of its binary characteristics. So the hardware implementation is easy and the computation can be accelerated.
7. Acknowledgment
The work in this paper is supported by the Fund of Science and Technology Development of CAEP. The number is 2009B0403043.
8. References
[1] F. H. Wang, Z. T. Huang and Y. Y. Zhou, “A Method for Blind Recognition of Convolution Code Based on Euclidean Algorithm,” IEEE International Conference on Wireless Communication Networking and Mobile Computing, Shanghai, 2007, pp. 1414-1417. doi:10.1109/ WICOM.2007.358
[2] P. Z. Lu, L. Shen, Y. Zou and X. Y. Luo, “Blind Recognition of Punctured Convolutional Codes,” Science in China, vol. 48, No. 4, 2005, pp. 484-498. doi: 10.1360/ 03yf0480
[3] J. J. Zan and Y. B. Li, “Blind Recognition of Low Code-Rate Binary Linear Block Code,” Radio Engineering of China, vol. 39, No. 1, 2009, pp. 19-24.
[4] J. Liu, N. Xie and X. Y. Zhou, “Blind Recognition Method of RS Coding,” Journal of Electronic Science and Technology, vol. 38, No. 3, March 2009, pp. 363- 367.
[5] S. Lin and D. J. Costello, “Error Control Coding,” 2nd Edition, Pearson Prentice Hall, Upper Saddle River, 2004, pp. 136-146.
[6] X. Wang, X. M. Wang and B. D. Wei, “An Efficient and Deterministic Algorithm to Determine Irreducible and Primitive Polynomials over Finite Fields,” Acta Scientriarum Naturalium Universitatis Sunyatseni, vol. 48, No. 1, 2009, pp. 6-9.

