Communications and Network
Vol.1 No.2(2009), Article ID:917,6 pages DOI:10.4236/cn.2009.12011
Uncertain IMM Estimator for Multi-Sensor Target Tracking
1School of Automation, Chongqing University of Posts and Telecommunications, Chongqing, China
2Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, China
3School of Electronics and Information Science, Sichuan University, Chengdu, China
E-mail: m_cen0104@sina.com, lxffxl666@126.com, dshluo@hotmail.com
Received July 17, 2009; accepted August 3, 2009
Keywords: Target Tracking, IMM, Uncertain Measurement, State Feedback
Abstract
Interacting Multiple Model (IMM) estimator can provide better performance of target tracking than mono model Kalman filter. In multi-sensor system ordinarily, availability of measurement from different sensors is stochastic, and it is difficult to construct uniform global observation vector and observation matrix appropriately in existing method. An IMM estimator for uncertain measurement is presented. By the method invalid measurement is regarded as outlier, and approximation is reconstructed by feedback of system state estimation of fusion center. Then nominally generalized certain measurement can be obtained by substituting reconstructed one for invalid one. The generalized certain measurement can be centralized to construct global measurement and provided to IMM estimator, and existing multi-sensor IMM estimation method is generalized to uncertain environment. Theoretical analysis and simulation results show the effectiveness of the method.
1. Introduction
In many applications of multi-sensor system, such as target tracking and surveillance, intelligent robot or wireless sensor networks (WSN), a group of heterogeneous sensors with different function and performance are integrated to operate cooperatively. Typical sensors include radar, vision-based sensor (including infrared, mono vision and stereo vision), acoustic or laser radar (lidar), and differ in field of view, resolution, range and procession interval. For instance, radar can measure the accurate distance of target in radial direction and support all-weather operation, but it has coarse measurement in angular direction. Reversely, vision-based sensor has sufficient lateral resolution, but the distance measurement is less accurate than radar. To estimate the state such as location, size, pose and motion information of maneuvering target accurately and reliably, multi-sensor fusion is necessary to exploit the advantages of each sensor [1–3].
Because of variant target maneuvering such as constant acceleration, swerving or constant speed cruising, and the transition between them, there are many dynamic models to characterize different target motion [4,5]. Because mono model tracking method can not adapt to the target maneuver correctly, then many multiple model approaches are available for target tracking and IMM method is used widely [6–8]. In IMM estimator, original measurement information, including measurement data and characteristic of precision, is centralized to construct global measurement, and filtered with multiple models and combined to obtain uniform optimal target state estimate. It is assumed in existing IMM algorithm that observation is available and covariance of measurement is known already. Because of various disturbances in measurement and communication, it is untenable to multi-sensor system that each sensor is valid at any time. In fact, uncertainty of measurement is one of the characteristics of multi-sensor system [9]. Because availability of measurement is not expressed, existing measurement fusion algorithm of IMM estimator is incomplete and inappropriate to apply without improving. Therefore, it is quite necessary to discuss IMM estimator for uncertain measurement. The estimate method of two sensors fusion with partial observation losses is discussed by linear matrix inequality method [10,11]. According to the equation of invalid measurement and valid measurement with infinite variance,the generalized measurement is reconstructed to denote the precision and availability of measurement [12].
An optimal measurement fusion IMM estimator is discussed in this paper, and a suboptimal one is brought forward to be convenient for numerical calculation of practical application. In the method invalid measurement is regarded as outlier, and generalized measurement is reconstructed based on target state feedback of IMM estimator.
2. IMM Estimator of Certain MeasurementFusion
Presuming there are n independent sensors and r models utilized in multi-sensor tracking system, target state and measurement equation of model i and sensor j are
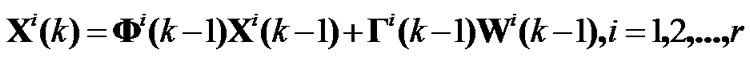
(1)
And
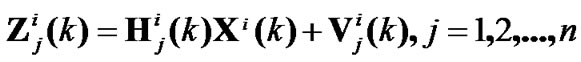 (2)
(2)
where Xi(k) is state vector, Φi(k-1) is state transfer matrix, Γi(k-1) is process noise input matrix of model i at time k. Zij(k) is observation vector of model i and sensor j at time k with corresponding observation spaceΩij, Hij(k) is observation matrix. Process noise {Wi(k)} and measurement noise {Vij(k)} are zero-mean white Gaussian noise sequence with covariance matrices Qi and Rij respectively, and Qi is symmetrical nonnegative matrix, Rij is symmetrical positive matrix. Then calculation process of multi-sensor IMM estimator can be described as follows.
Step 1: Global measurement constructing
The first step of multi-sensor IMM estimator is constructing global measurement from sensors. It is assumed in existing measurement fusion algorithm that measurement of each sensor is valid constantly, then uniform global observation vector can be constructed by centralizing all measurement to form global measurement vector Zi(k)∈Ωi [13,14], where
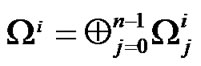 (3)
(3)
Global observation equation corresponding to model i is expressed as
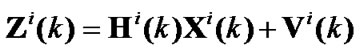 (4)
(4)
where
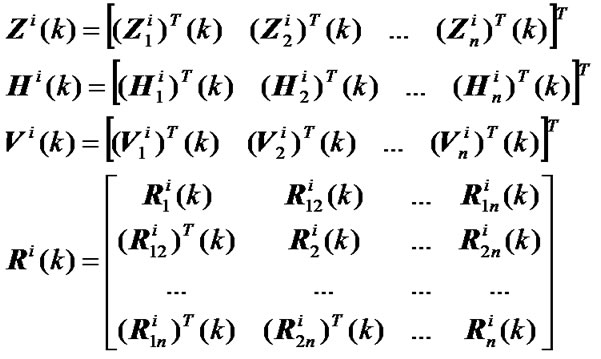 (5)
(5)

Figure 1. Constructing of global measurement.
Hi(k) is global observation matrix, Vi(k) and Ri(k) is observation noise and covariance corresponding to model i respectively. Equations (1) and (3) constitute state transfer and observation equation of Kalman filter based IMM estimator.
Step 2: Model interacting
Let pij denote Markov transition probability and μi(k) denote the probability of the mode i at time k, model interacting is calculated as
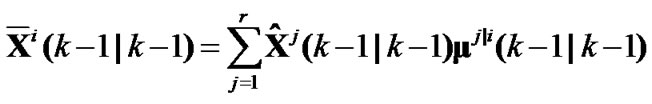 (6)
(6)
and
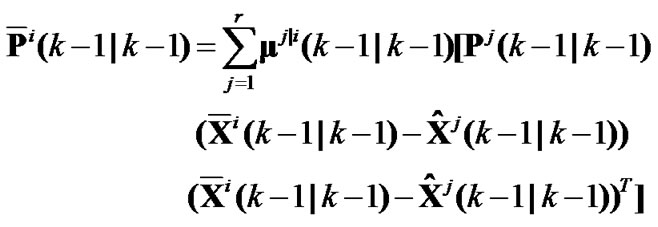 (7)
(7)
where i=1,2,..,r,
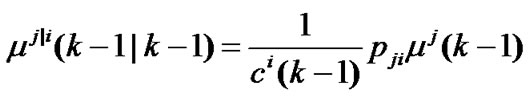 (8)
(8)
is mixing probabilities, and
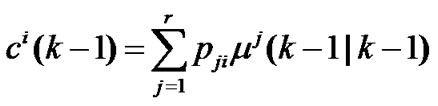 (9)
(9)
is normalizing factor.
Step 3: Model filtering
Based on r models from (4) and corresponding to global measurement Zi(k), target state and covariance estimation 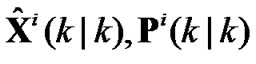 is calculated by Kalman filters.
is calculated by Kalman filters.
State prediction equations are
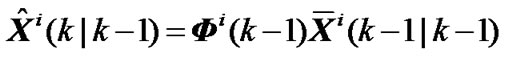 (10)
(10)
 (11)
(11)
Filtering updating equations are
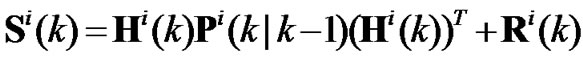 (12)
(12)
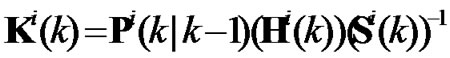 (13)
(13)
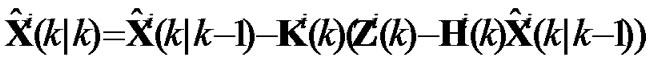 (14)
(14)
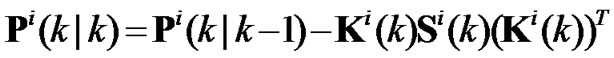 (15)
(15)
Step 4: Model probability updating
The likelihoods of each model are calculated as
 (16)
(16)
where Vi(k) is residual of model i with zero mean and the covariance Si(k), N is Gaussian distribution. Then probabilities of each model are calculated as
 (17)
(17)
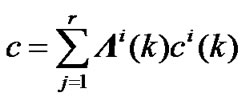 (18)
(18)
Step 5: State estimation and covariance fusion
State estimation and associated covariance are combined by
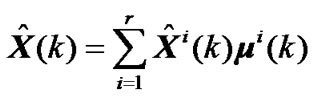 (19)
(19)
and
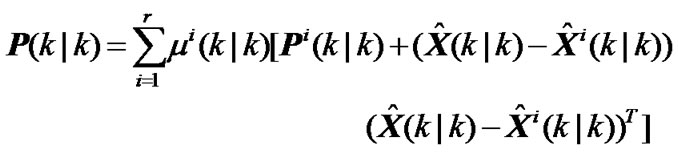 (20)
(20)
i.e. total state estimation is probabilistic weighted summation of every filters.
The method above differs from ordinary IMM estimator in Step 1 where global measurement is constructed by multiple sensors. Because of the presuming that measurement of any sensor is valid constantly, the method is a certain algorithm.
To multi-sensor tracking system with different performance and complicated environment, uncertainty of measurement is one of the characteristics, and it is necessary to discuss IMM estimator for uncertain measurement.
3. IMM Estimator for UncertainMeasurement
3.1. Optimal Uncertain IMM Estimator
To any sensor i, it is possible that some element zii,j(k) of observation vector Zii(k)∈Ωii is invalid at time k. When invalid measurement exists in multi-sensor system, if certain method is applied to construct global measurement by (4) and (5), because availability of measurement is not considered in certain method and all measurement data are regarded as valid ones, the global observation vector Zi(k) is incorrect and filters of IMM estimator can perform incorrectly.
The problem above can be resolved by only combining valid measurement data to construct new observation space 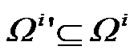 and new global observation equation. Because of any measurement of any sensor being invalid by any possibility, the type and amount of invalid data are uncertain, i.e. to any
and new global observation equation. Because of any measurement of any sensor being invalid by any possibility, the type and amount of invalid data are uncertain, i.e. to any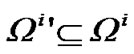 , Zi(k)∈Ωi′ may be valid. Thus constructing different Zi(k) and observation equation in different Ωi′ is required in each filter and each filtering step. Apparently, to satisfy all the conditions of uncertain measurement, the amount of filters corresponding to model i is
, Zi(k)∈Ωi′ may be valid. Thus constructing different Zi(k) and observation equation in different Ωi′ is required in each filter and each filtering step. Apparently, to satisfy all the conditions of uncertain measurement, the amount of filters corresponding to model i is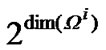 , and the total amount of filters in IMM estimator will be
, and the total amount of filters in IMM estimator will be
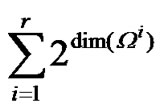
Then extreme complexity and inconvenience is resulted, and the resolution is difficult to be applicable.
Because there is no parameter to express availability of measurement in fusion filters of IMM estimator, apparently existing method can not solve the problem of invalid data in uncertain measurement appropriately. Then it is necessary to generalize existing method. If uncertainty of measurement is avoided by reconstructing the measurement, existing filtering method of IMM estimator can be applicable.
In state estimate equation of Kalman filter (14), the proportion of Zi(k) and 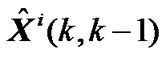 in
in 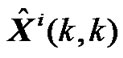 is determined by filter gain Ki(k). If Ki(k) reduces, the proportion of Zi(k) will reduce and the one of
is determined by filter gain Ki(k). If Ki(k) reduces, the proportion of Zi(k) will reduce and the one of  will increase. Ki(k) is determined by Ri(k) and Pi(k, k-1) according to (12) and (13). If Ri(k) increase, Ki(k) will reduce and the proportion of Zi(k) will reduce also. In limit case, when ||R(k)||→∞, it is satisfied that ||K(k)||→0, and Equation (7) will be
will increase. Ki(k) is determined by Ri(k) and Pi(k, k-1) according to (12) and (13). If Ri(k) increase, Ki(k) will reduce and the proportion of Zi(k) will reduce also. In limit case, when ||R(k)||→∞, it is satisfied that ||K(k)||→0, and Equation (7) will be
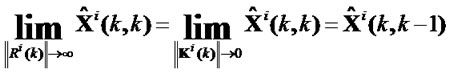 (21)
(21)
here Zi(k) has no effect on optimal estimation of target state, and it is equivalent to that Zi(k) is invalid when ||Ri(k)||→∞. Then Ri(k) can indicate the available extent of measurement. Ri(k) only denotes precision of valid measurement in existing algorithm, and is necessary to be generalized.
To evaluate availability of measurement, availability function of zii,m(k), i.e. component m of Zii(k) corresponding to sensor i at time k is defined as
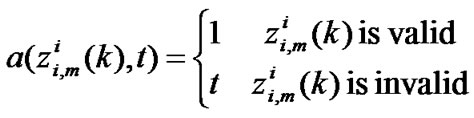 (22)
(22)
Then Rii(k)=[rii,lm(k)] of Zii(k) can be generalized as
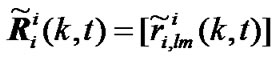 (23)
(23)
and
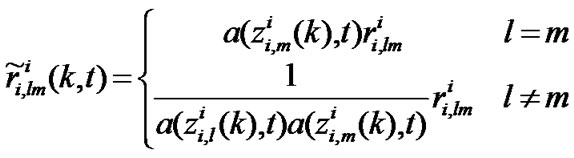 (24)
(24)
where a(zii,l(k), t) and a(zii,m(k), t) is availability function of component i and j of Zii(k). It means that when zii,l(k) and zii,m(k) are valid, availability functions equal to 1 and 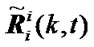 =Rii(k). When zii,l(k) or zii,m(k) is invalid, corresponding availability function tends to infinite, i.e. a(zii,l(k), t)→∞ or a(zii,m(k), t)→∞, and variance of invalid measurement will tend to infinite also and be irrelevant to other measurement.
=Rii(k). When zii,l(k) or zii,m(k) is invalid, corresponding availability function tends to infinite, i.e. a(zii,l(k), t)→∞ or a(zii,m(k), t)→∞, and variance of invalid measurement will tend to infinite also and be irrelevant to other measurement.
By defining availability function to reconstruct generalized variance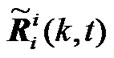 , uncertainty of measurement is avoided formally and existing fusion filtering method can be applicable to IMM estimator. Constructing Zi(k, t) from {Zim(k), m=1,2,…,n} according to (4)-(5) and
, uncertainty of measurement is avoided formally and existing fusion filtering method can be applicable to IMM estimator. Constructing Zi(k, t) from {Zim(k), m=1,2,…,n} according to (4)-(5) and 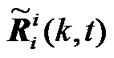 from (22)–(24), multi-sensor IMM estimator is achieved and estimation of target state
from (22)–(24), multi-sensor IMM estimator is achieved and estimation of target state 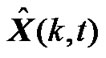 is obtained according to (6)–(20). Let t→∞, optimal estimation of target state from IMM estimator without parameter t is obtained as
is obtained according to (6)–(20). Let t→∞, optimal estimation of target state from IMM estimator without parameter t is obtained as
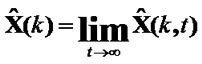 (25)
(25)
3.2. Suboptimal IMM Estimator Based onTarget State Feedback
It is inconvenient in practical application that availability function is defined using limit operation t→∞ according to (25). To solve the problem, invalid measurement can be regard as outlier, and corresponding valid measurement can be reconstructed with target state feedback of IMM estimator approximatively.
In target tracking system, when target is faint or interference is strong, there are outliers in measurement sequence ordinarily and tracking accuracy reduces. Presuming measurement Zii(k) of sensor i at time k is outlier, typical solution is discarding Zii(k) and reconstructing one step prediction of the observation 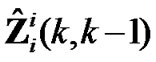 by state estimation of
by state estimation of 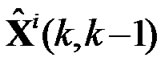 according to (10) as
according to (10) as
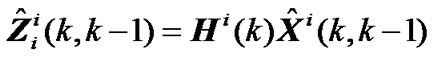 (26)
(26)
Substituting  for Zii(k) to filter, the effect of outliers can be avoided. Defining generalized measurement as
for Zii(k) to filter, the effect of outliers can be avoided. Defining generalized measurement as
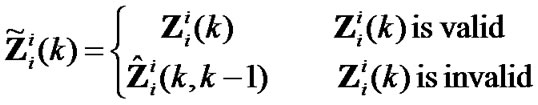 (27)
(27)
And keeping covariance matrix Rii(k) invariant, the invalid measurement is converted to approximate generalized one having availability always.
When all measurement is valid, each generalized measurement in (27) is equal to corresponding actual measurement, and IMM estimator for uncertain measurement is degenerated to certain one. Therefore, existing method is a special case of method presented and the latter is more general.
Compared to existing method, IMM estimator for uncertain measurement presented only adds a calculation step of constructing generalized measurement  in (26),(27). Calculational cost of this step can be ignored almost comparing to one of IMM algorithm, so that calculational cost of uncertain method presented is almost as the same as certain one.
in (26),(27). Calculational cost of this step can be ignored almost comparing to one of IMM algorithm, so that calculational cost of uncertain method presented is almost as the same as certain one.
4. Simulation Results
To evaluate effect of method presented, simulation data are obtained from a multi-sensor target tracking system including two detectors with different precision. The target moves with constant velocity at time ,
,  and
and , with constant acceleration at time
, with constant acceleration at time  and
and . The perfect state of target is shown in Figure 2.
. The perfect state of target is shown in Figure 2.
It is assumed that IMM estimator is composed of two filters based on CA and CV model respectively. Markov transition probability is [0.95 0.05; 0.05 0.95], and the probability of two models are 0.5 at initial time. Sam
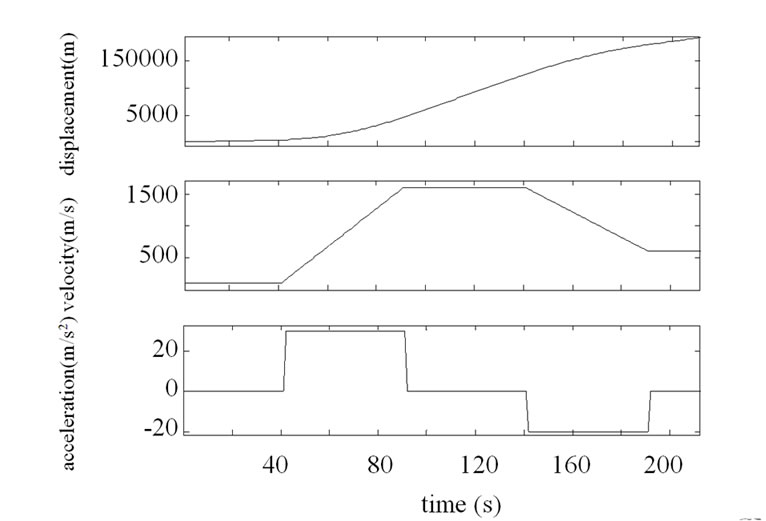
Figure 2. The perfect state of target.
pling time is T=1s, process noise is σ=10m, observation noise of detector 1 is σ1=100m and that of detector 2 is σ2=10m. Let detector 1 is valid and detector 2 is invalid at , detector 1 is invalid and detector 2 is valid at
, detector 1 is invalid and detector 2 is valid at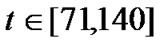 , and detector 1 and 2 are both valid at
, and detector 1 and 2 are both valid at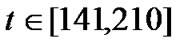 , and target state are estimated by the method presented at each moment. Executing simulation 10 times, and calculating standard deviation of estimation errors at each moment, the results of three uncertain cases are shown in Figure 3.
, and target state are estimated by the method presented at each moment. Executing simulation 10 times, and calculating standard deviation of estimation errors at each moment, the results of three uncertain cases are shown in Figure 3.
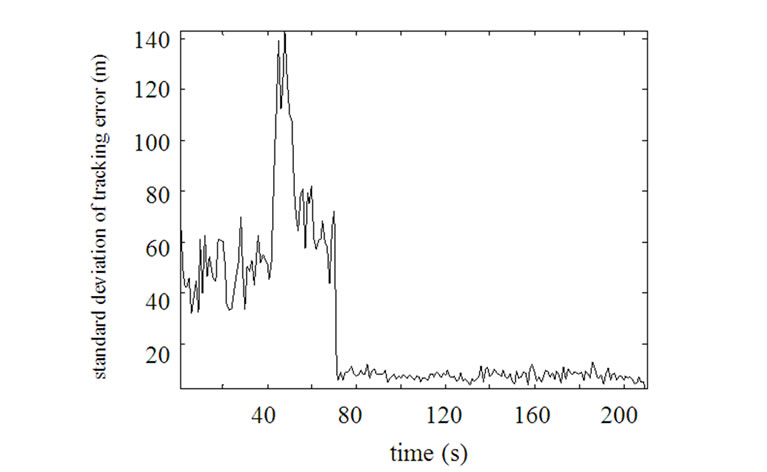
Figure 3. Standard deviation of tracking error (σ1=100, σ2=10).
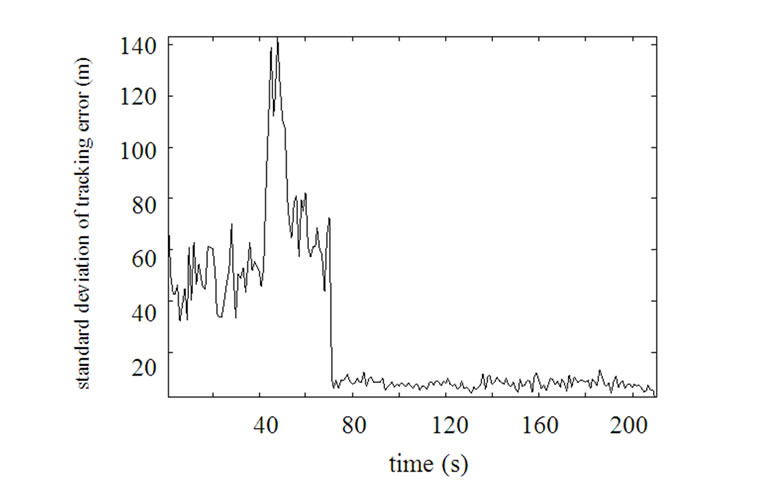
Figure 4. Standard deviation of tracking error (σ1=100, σ2=50).
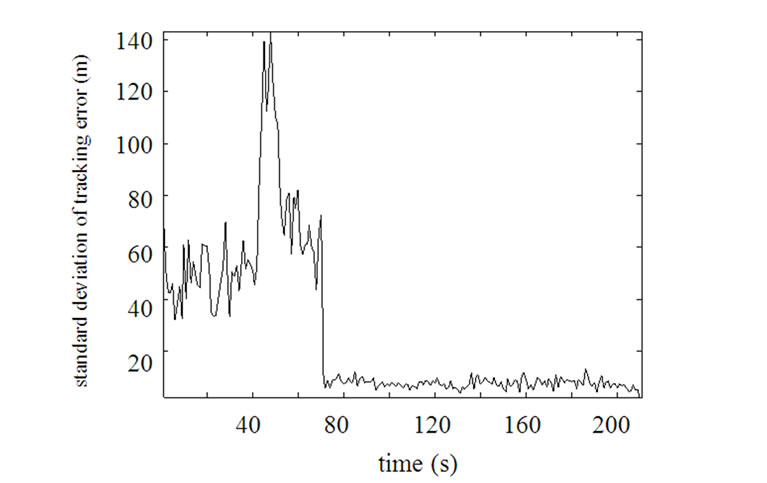
Figure 5. Standard deviation of tracking error (σ1=100, σ2=100).
Performing the simulation with σ2=50m and σ2=100m respectively, the result is shown in Figure 4 and Figure 5.
In situation 1 and 2 only one sensor is valid. From Figure 3, since σ1>>σ2, tracking error of situation 1 is comparative larger than that of situation 2. Each sensor is valid in situation 3, so tracking error of situation 3 is least. Because σ1>>σ2 similarly, estimation result of target state is determined by measurement of detector 2 mainly and almost the same as which of the situation 2. From Figures 4 and 5, there are 2 valid sensors at , and corresponding tracking error is least.
, and corresponding tracking error is least.
Simulation results demonstrate a typical scenario of multi-sensor IMM estimator for uncertain measurement. The results are consistent with theoretic analyses, so method presented can solve the problem of multi-sensor IMM estimator with varied validity preferably. Simultaneously calculational cost of method presented is almost the same as existing one.
5. Conclusions
In multi-sensor system there’s invalid measurement sometimes, and uncertainty of measurement is one of the typical characteristics. Existing IMM estimator is a certain algorithm where it is presumed that all measurement is valid always, so it can not perform uncertain measurement appropriately.
One of approaches to avoid uncertainty of measurement defines availability function for each component of observation vector and reconstructs observation covariance matrix to express uncertainty of measurement. But limit operation is involved in this approach. The approach presented substitutes target state feedback for invalid measurement to reconstruct generalized measurement. Then target state estimation can be obtained by existing IMM estimator with generalized measurement, and existing method is generalized and as a special case of uncertain one presented.
6. References
[1] S. Tokoro, K. Moriizumi, T. Kawasaki, T. Nagao, K. Abe, and K. Fujita, “Sensor fusion system for pre-crash safety system,” Proceedings of 2004 IEEE Intelligent Vehicles Symposium, pp. 945–950, 2004.
[2] A. Polychronopoulos, M. Tsogas, A. J. Amditis, and L. Andreone, “Sensor fusion for predicting vehicles’ path for collision avoidance systems,” IEEE Transactions on Intelligent Transportation Systems, Vol. 8, No. 3, pp. 549–562, 2007.
[3] G. Alessandretti, A. Broggi, and P. Cerri, “Vehicle and guard rail detection using radar and vision data fusion,” IEEE Transactions on Intelligent Transportation Systems, Vol. 8, No. 1, pp. 95–105, 2007.
[4] X. R. Li and V. P. Jilkov, “Survey of maneuvering target tracking, Part I: Dynamic models,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 39, No. 4, pp. 1333–1364, 2003.
[5] H. Zhou, Z. Jing, and P. Wang, “Maneuver target tacking,” National Defence Industry Press, Beijing, 1991.
[6] X. R. Li and V. P. Jilkov, “Survey of maneuvering target tracking, Part V: Multiple-model methods,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 41, No. 4, pp. 1255–1321, 2005.
[7] E. Mazor, A. Averbuch, Y. Bar-Shalom, and J. Dayan, “Interacting multiple model methods in target tracking: A survey,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 34, No. 1, pp. 103–123, 1998.
[8] M. Mallick and B. F. La Scala, “IMM estimator for ground target tracking with variable measurement sampling intervals,” Proceedings of 9th International Conference Information Fusion, pp. 1–8, 2006.
[9] H. Chen and P. Meer, “Robust fusion of uncertain information,” IEEE Transactions on Systems, Man and Cybernetics, Part B, Vol. 35, No. 3, pp. 578–586, 2005.
[10] X. Liu and A. Goldsmith, “Kalman filtering with partial observation losses,” Proceedings of 43rd IEEE Conference Decision and Control, Vol. 4, pp. 4180–4186, 2004.
[11] Z. Wang, D. W. C. Ho, and X. Liu, “Variance-constrained filtering for uncertain stochastic systems with missing measurements,” IEEE Transactions on Automatic Control, Vol. 48, No. 7, pp. 1254–1258, 2003.
[12] M. Cen and C. Fu, “Combined measurement fusion of unequal dimensional measurement vectors,” Journal of Sichuan University (Engineering Science Edition), Vol. 38, No. 4, pp. 45–149 (Ch), 2006.
[13] G. Qiang and C. J. Harris, “Comparison of two measurement fusion methods for Kalman-filter-based multisensor data fusion,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 37, No. 1, pp. 273–280, 2001.
[14] J. A. Roecker and C. D. McGillem, “Comparison of two-sensor tracking methods based on state vector fusion and measurement fusion,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 24, No. 4, pp. 447–449, 1988.

