Received 5 May 2016; accepted 17 June 2016; published 20 June 2016

ABSTRACT

This paper mainly studies some properties of skew polynomial ring related to Morita invariance, Armendariz and (quasi)-Baer. First, we show that skew polynomial ring has no Morita invariance by the counterexample. Then we prove a necessary condition that skew polynomial ring constitutes Armendariz ring. We lastly investigate that condition of skew polynomial ring is a (quasi)-Baer ring, and verify that the conditions is necessary, but not sufficient by example and counterexample.

Keywords:

Skew Polynomial Ring, (Quasi)-Baer Ring, Armendariz Ring, Morita Context Ring, Morita Invariance, Nozero Divisor Ring

1. Introduction

Throughout this paper every ring is an associative with identity unless otherwise stated. Given a ring R, 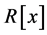, , 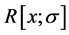, , 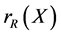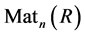and 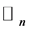denote the polynomial ring with an indeterminate x over R, the skew polynomial ring over R, the right annihilator of nonempty subset X of ring R, the left annihilator of nonempty subset X of ring R, and the 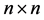matrix ring over R, the ring of integers modulo n, respectively. A ring 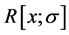is called Skew polynomial ring if 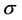is an endomorphism over R; operations are usual addition and multiplication defined by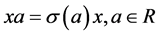. In [1] , that skew polynomial ring has no Morita invariance. A ring R is called Armendariz ring if implies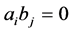, where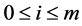, 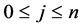for any

, in [2] . If R is a semiprime ring, then skew polynomial ring

is a quasi-Armendariz ring by [3] . G. F. Birkenmeier first introduced the concept of Baer ring, and proved that Baer ring is quasi-Baer ring, but converse is not hold, and right principally quasi-Baer ring has Morita invariance by [4] . Q.J. Song gave the condition that iterated skew polynomial ring constitutes (quasi)-Baer ring by [5] . We will show that skew polynomial ring has no Morita invariance by the counterexample, and the condition that skew polynomial ring has properties of Armendarizand (quasi)-Baer, and verify that the condition is necessary, but not sufficient by example and counterexample.

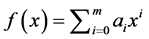2. Preliminary

Definition 2.1. [6] Let R and S be rings, then R and S are Morita equivalent if there exists projective module, such that. Morita invariance is the invariant property under Morita equivalent rings.

Lemma 2.2. [6] The ring R and S are Morita equivalent, if and only if there exists an integer n and idempotent, such that and.

Definition 2.3. [7] A ring R is called (quasi)-Baer ring if the right annihilator of (resp. right ideal) nonempty subset of R is generated by an idempotent as a right ideal.

Lemma 2.4. Suppose that R is a ring has no zero divisor and is a monomorphism over R, then skew polynomial ring has no zero divisor.

Proof. For any, , if

then all coefficients of the skew polynomial are zero. Since is a monomorphism and R has no zero divisor, so implies, implies or. Case 1. If, , then. Since, so. Simlarly, we show , thus. Case 2. If, , then. Because, so,. Similarly, , thus. Case 3. If, , so,. Similarly, or for, , then or.Therefore is a ring has no divisor of zero.

Definition 2.5. [8] A ring R is called a reversible, if implies for any.

Proposition 2.6. [9] Every reduced ring is a reversible ring, but the converse does not hold.

Proposition 2.7. Let R be a reduced ring, then the coefficients of right annihilator of any polynomial over are the right annihilator of all coefficients of the polynomial.

Proof. For any, , let, then, so, ,

, , and. Because R be a reduced ring, hence R be a reversible ring, so. Because, then, so, so, thus and, so, so and. Since, we have, then, so, so and, so, so, hence, so, , so, thus, Similarly, we have, which,. Therefore the coefficients of right annihilator of any polynomial over are the right annihilator of all coefficients of the polynomial.

Proposition 2.8. Let R be a reduced ring, then the idempotent of ring R is the idempotent of.

Proof. For any, if, we have

then. Since R is a reduced ring and, , so,. Similarly, we have, and because, so. Thus, which is the idempotent of.

3. Main Results

The property of skew polynomial ring relation to Morita invariance , we have the following counterexample.

Example 3.1. Suppose that a ring and is an endomorphism over, define the usual addition and multiplication by for any, then is a skew polynomial ring, but has no Morita invariance.

In fact, clearly, is a skew polynomial ring. Consider a ring, which, , , , we have all idempotents of are, , , , ,. Suppose that.

Case 1. If, then

Case 2. If, then. Case 3. If, then . Similarly, we show that for all idempotente. Clearly, the condition of is not true for any integer n, so and any ring S are not Morita equivalent by lemma 2.2, therefore has no Morita invariance.

So the skew polynomial ring has no Morita invariance by the counterexample. The following theorem shows that the condition of skew polynomial ring constitutes Armendariz ring.

Theorem 3.2. Let R be a ring that has no zero divisor and be a monomorphism over R, then skew polynomial ring is an Armendariz ring.

Proof. Since R has no zero divisor, so has no zero divisor by lemma2.4, then is a reversible ring. For any, , and, , if

then the all coefficients of are zero. Since, , so, and hence,. Because, , so, , and have,. Similarly, . Thus the skew polynomial ring of no zero divisor is an Armendariz ring.

Next research the necessary and sufficient of this condition by the following example.

Example 3.3. Let be a ring with a monomorphism defined by. For any, , define the usual addition and multiplication by, then is a skew polynomial ring, but is not an Armendariz ring.

In fact, clearly, is a skew polynomial ring. Let, , if, then all coefficients of the skew polynomial are zero. But, , thus is not an Armendariz ring.

It derives from the above example 3.3 that we further verify the condition is necessary. Next we study that skew polynomial ring is a (quasi)-Baer ring under the condition of no zero divisor .

Theorem 3.4. Let R be a ring that has no zero divisor and is an endomorphism over R, then skew polynomial ring is a (quasi)-Baer ring.

Proof. For any, , let. If, then is any polynomial ring, and has. If, there exists, such that, then. And because R is a ring has no ze-

ro divisor, so or. Since arbitrary of and i, we have implies, so. Thus the right annihilators set of any nonempty subset X is. So is a Baer ring, and is a quasi-Baer ring by [5] .

The following example shows that skew polynomial ring is (quasi)-Baer ring.

Example 3.5. Let be a ring with an endomorphism defined by, then is a skew polynomial ring, and is a (quasi)-Baer ring.

In fact, clearly, R is a field, so R is a no zero divisor ring. Therefore the right annihilator of every nonempty subset is, then the right ideal generated by the idempotent 0. Thus is a (quasi)-Baer ring clearly by theorem 3.4.

So we proof the condition of no zero divisor is necessary. The following counterexample shows that the condition is not sufficient condition that skew polynomial ring is a (quasi)-Baer ring.

Example 3.6. Suppose that be a ring with an endomorphism defined by over R, for any, , define the usual addition and multiplication is defined by, then is a skew polynomial ring, but is not a (quasi)-Baer ring.

In fact, clearly, is a skew polynomial ring. For any, if, then, , ,.We have all idempotents of are, , ,. Let, since

which. Thus is not a (quasi)-Baer ring.

4. Conclusion

Inthis paper, we show that skew polynomial ring has no Morita invariance by the counterexample, and give the condition that skew polynomial ring constitutes Armendariz and (quasi)-Baer ring, and verify that the condition is necessary, but not sufficient.

Acknowledgements

The authors thank the referee for very careful reading the manuscript and many valuable suggestions that improved the paper by much. This work was supported by the National Natural Science Foundation of China (11361063).

Cite this paper

Qianqian Chu,Hailan Jin, (2016) The Some Properties of Skew Polynomial Rings. Advances in Pure Mathematics,06,507-511. doi: 10.4236/apm.2016.67037

References

NOTES

^*Corresponding author.